基于結構參數的硅諧振式加速度計頻率特性分析

郭雪濤，李逸倫，李鵬飛

（中國航空工業集團公司西安飛行自動控制研究所,西安710065）

0 引言

相比于傳統擺式加速度計,硅諧振式加速度計具有高分辨率、寬動態范圍與準數字輸出等優勢,已成為加速度計發展的一個重要方向之一[1]。近年來,隨著MEMS制造工藝的持續發展,國內外越來越多的MEMS研制機構可制造出更高精度的微型器件結構尺寸,同時保持更低廉的制造成本。綜上,硅諧振式加速度計獲得了前所未有的發展機遇。

在硅諧振式加速度計中,諧振器為加速度計的核心部件,諧振器設計的合理性對硅諧振式加速度計的性能有至關重要的影響。雙端固支音叉（Double-ended Tuning Fork,DETF）作為一種典型的諧振器,具有結構簡單、易于加工等優勢[2],廣泛應用于硅諧振式加速度計中。DETF的結構設計關乎整個傳感器的靈敏度、分辨率和標度因數等參數,故DETF的結構設計與優化對硅諧振式加速度計的設計非常重要。

國內外學者對DETF的結構設計與優化開展了一定的研究工作。2017年,北京化工大學的Shi等[3]基于不確定分析理論研究了加速度計DETF的設計與優化,為硅諧振式加速度計的研究提供了參考。2017年,中國工程物理研究院的高揚等[4]提出了一種高性能氮化鋁差分諧振式加速度計結構,從理論與仿真方面對其設計作了一定的研究工作。2016年,意大利米蘭理工大學的Comi等[5]提出了一款新型的Z軸硅諧振式加速度計,采用了諧振器與電容搭配的形式,拓寬了硅諧振式加速度計的形式與功能。此外,還有很多學者在提出不同結構的硅諧振式加速度計時,對其結構也做了相應的設計與分析。

以上文獻在分析DETF的結構時,均按照音叉兩端固定的方式討論DETF的諧振頻率以及加速度計的靈敏度、分辨率等參數,但諧振式加速度計在實際工作中僅有一端完全固定在基底,而另一端屬于活動端,通常連接于微型杠桿的輸出桿,用于傳遞由加速度施加在質量塊上的應力。因此,采用兩端固定的方式仿真設計諧振器的音叉結構,在邊界條件上的不準確必然會造成仿真結果與結構分析的偏差。此外,上述文獻在結構仿真與分析過程中忽視了諧振梁上的梳齒結構對諧振頻率產生的影響。本文針對上述問題,基于諧振器的具體工作環境建立了模型,仿真分析了其關鍵結構參數對諧振器諧振頻率的影響規律。

1 硅諧振式加速度計的工作原理

硅諧振式加速度計主要由以下幾個部分組成:DETF、梳齒結構、微型杠桿結構、質量塊和支撐梁,如圖1所示。質量塊在加速度的作用下產生慣性力,微型杠桿結構對其放大n倍后,經微型杠桿結構的輸出桿傳遞到DETF諧振器上,諧振器由于存在應力導致其諧振頻率發生相應的變化,通過檢測諧振頻率的變化量即可得到加速度值。同時,為了減小外部環境共模誤差的影響,提高加速度計精度,諧振器的結構大多采用兩個對稱分布的DETF結構。在該型結構下,當有加速度輸入時,一個DETF受張力,另一個DETF受拉力,使得它們的諧振頻率分別增加與減小。經過信號的差分處理,即可得到它們的差動頻率,在一定的輸入加速度范圍內,其值與輸入加速度值成近似線性關系。

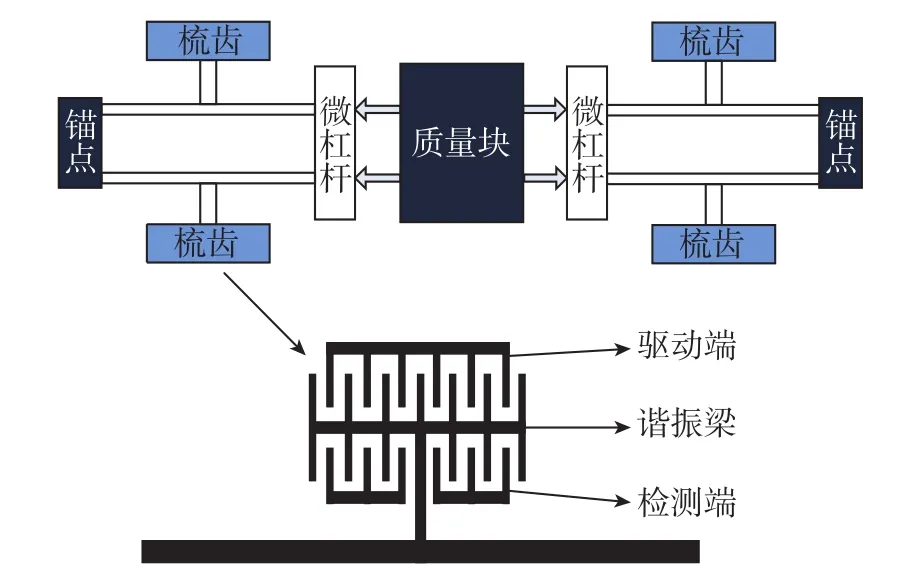
圖1 硅諧振式加速度計結構示意圖Fig.1 Structure diagram of silicon resonant accelerometer

1.1 DETF諧振器的固有頻率及靈敏度

對于一般的DETF諧振器,其固有頻率[6]為

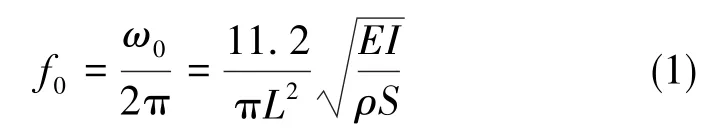
當諧振梁存在軸向力F時,其固有頻率為

則差分式諧振式加速度計的諧振頻率變化量為

運用Taylor公式展開,同時略去高次項,代入轉動慣量得

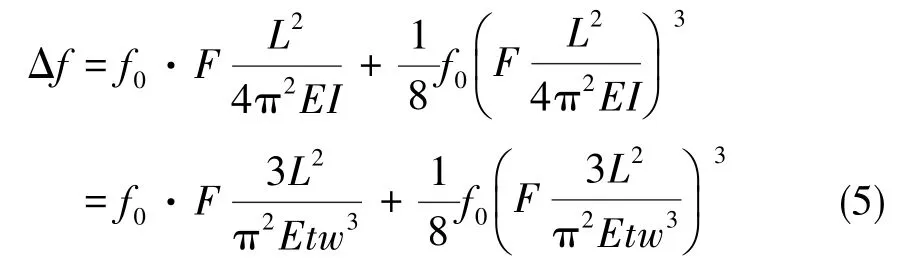
根據式（6）,諧振式加速度計的靈敏度僅與加速度計材料的楊氏模量、諧振梁的厚度與寬度有關,與諧振梁的長度無關。

1.2 DETF諧振器的振動模態

DETF諧振器的前四階振動模態如圖2所示。

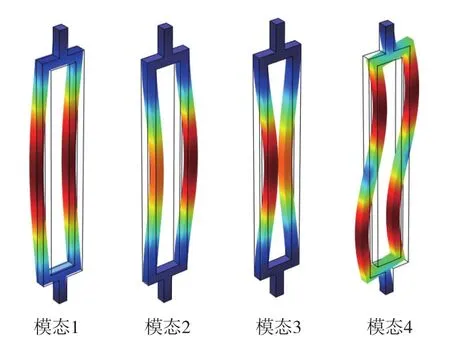
圖2 DETF振動模態Fig.2 Vibration modals of DETF

由圖2可知,模態3稱為面內對稱模態[7],為諧振式加速度計的工作模態,模態1、模態2、模態4均為干擾模態。在諧振器工作時,模態3下的兩個音叉分別向著相反的方向振動,它們的合并區域即連接梁部分產生的應力和力矩的方向相反、大小相等、相互抵消,從而整個結構與外界的能量耦合較小,可提高整個傳感器的Q值。

2 諧振器結構仿真

如圖3所示,仿真的加速度計為硅結構的微型諧振加速度計,諧振器由諧振梁、支撐梁、連接梁（連接加速度計質量塊與微杠桿）、梳齒結構以及錨點組成。加速度計的質量塊與微杠桿結構由于只起到對諧振梁施加與放大加速度所產生的力,故在圖3中未畫出。圖示的諧振器采用錨點內置的布局,該布局有利于減小由于硅的熱膨脹而導致的加速度計的溫度漂移[8]。

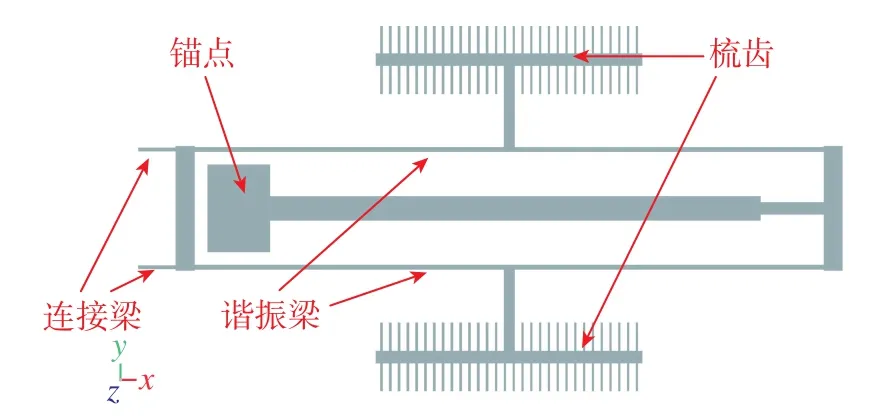
圖3 諧振器結構示意圖Fig.3 Diagram of resonator structure

根據硅諧振式加速度計工作的實際環境,仿真邊界條件設置如下:1）錨點底面設置為固定約束；2）加速度計質量塊由加速度產生的力經過微杠桿放大,施加于連接梁端部橫截面,施加方式為面載荷；3）整個音叉諧振器部分受到由加速度產生的體載荷力與自身的重力。

上述諧振器結構采用COMSOL Multiphysics進行參數化仿真,目的在于比較分析諧振器的關鍵結構尺寸對其諧振頻率的影響程度。仿真中,加速度輸入范圍為:0g～60g,通過對仿真的諧振器施加較大的加速度量值,來減小仿真計算的非線性帶來的靈敏度誤差。

（1）諧振梁寬度

圖3所示諧振器的諧振梁初始寬度為8μm、初始厚度為60μm、初始梁長度為1000μm、兩個諧振梁之間的間距為191μm。仿真過程中,依次將諧振梁的寬度增加1μm,取5個仿真數值點。首先,其對應結構下未施加加速度時,工作諧振頻率的仿真結果如圖4所示。

圖4 諧振梁寬與諧振頻率的關系Fig.4 Relationship between resonant beam width and resonant frequency

由圖4可知,隨著梁寬的增加,諧振頻率呈線性增長,其梁寬引起的諧振頻率變化的靈敏度為4622.5Hz/μm。在0g～60g的加速度輸入范圍內,對上述5種結構進行加速度的靈敏度仿真分析,處理結果如圖5所示。

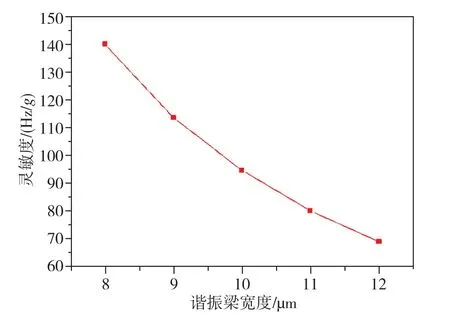
圖5 諧振梁寬與加速度靈敏度的關系Fig.5 Relationship between resonant beam width and acceleration sensitivity

由圖5可知,諧振梁寬度與加速度靈敏度呈冪函數關系,其數值分析的函數表達式為y＝5289.5x－1.747。隨著梁寬的增加,加速度靈敏度減小的數值在降低。

（2）諧振梁厚度

諧振器的梁寬取10μm,厚度初始值為40μm,其余結構參數不變。仿真過程中,依次將諧振梁的厚度增加5μm,取9個仿真數值點。首先,其對應結構在未施加加速度時,工作諧振頻率的仿真結果如圖6所示。

圖6 諧振梁厚與諧振頻率的關系Fig.6 Relationship between resonant beam thickness and resonant frequency

由圖6可知,諧振梁厚度越厚,諧振器的諧振頻率越高,且兩者呈近似線性關系,曲線中間的波動是由于有限元軟件的計算誤差所致。通過線性擬合,其梁厚引起的靈敏度為6.23Hz/μm。

在0g～60g的加速度輸入范圍內,以10μm為步長,初始梁厚為40μm,取5個點進行加速度的靈敏度仿真,處理結果如圖7所示。

圖7 諧振梁厚與加速度靈敏度的關系Fig.7 Relationship between resonant beam thickness and acceleration sensitivity

由圖7可知,與諧振梁寬度結果相似,諧振梁厚度與加速度靈敏度呈冪函數關系,其數值分析的函數表達式為y＝7067x－1.053。隨著梁厚的增加,加速度靈敏度減小的數值也在降低。

（3）諧振梁長度

諧振梁寬度取8μm,厚度取60μm,初始梁長度取1000μm,其余結構參數不變。仿真過程中,依次增加10μm梁長,取5個仿真數值點。首先,研究其未施加加速度時的工作諧振頻率變化情況,如圖8所示。

圖8 諧振梁長與諧振頻率的關系Fig.8 Relationship between resonant beam length and resonant frequency

由圖8可知,諧振梁長與諧振器頻率為線性關系。梁長越長,諧振頻率越小,其靈敏度為－38.87Hz/μm。

在0g～60g加速度輸入范圍內,對上述5種結構進行加速度靈敏度仿真,處理結果如圖9所示。

圖9 諧振梁長與加速度靈敏度的關系Fig.9 Relationship between resonant beam length and acceleration sensitivity

由圖9可知,諧振梁長不會影響諧振器的加速度靈敏度,該結論與式（6）所推導出的結果一致。仿真結果中,仍有靈敏度隨梁長增加而增長的現象,這是由于模型存在梳齒、錨點與支撐點部分,梁長的改變使得整個模型的重心發生微小的變化,從而影響了諧振器的加速度靈敏度。

（4）其他關鍵結構仿真

諧振器的梁寬取10μm,厚度取50μm,梁長取1000μm,對諧振器兩個諧振梁之間的間距進行仿真,初始間距為191μm,選取間距為200μm、220μm與240μm的結構。首先,對其未施加加速度時的工作諧振頻率進行仿真,結果如圖10所示。

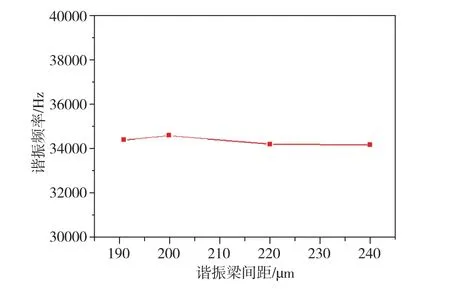
圖10 諧振梁間距與諧振頻率的關系Fig.10 Relationship between resonant beam spacing and resonant frequency

由圖10可知,諧振梁間距的改變對諧振器諧振頻率的改變影響很小,諧振頻率始終保持在34000Hz左右。

在0g～60g加速度輸入范圍內,對上述4種結構進行加速度靈敏度仿真,處理結果如圖11所示。

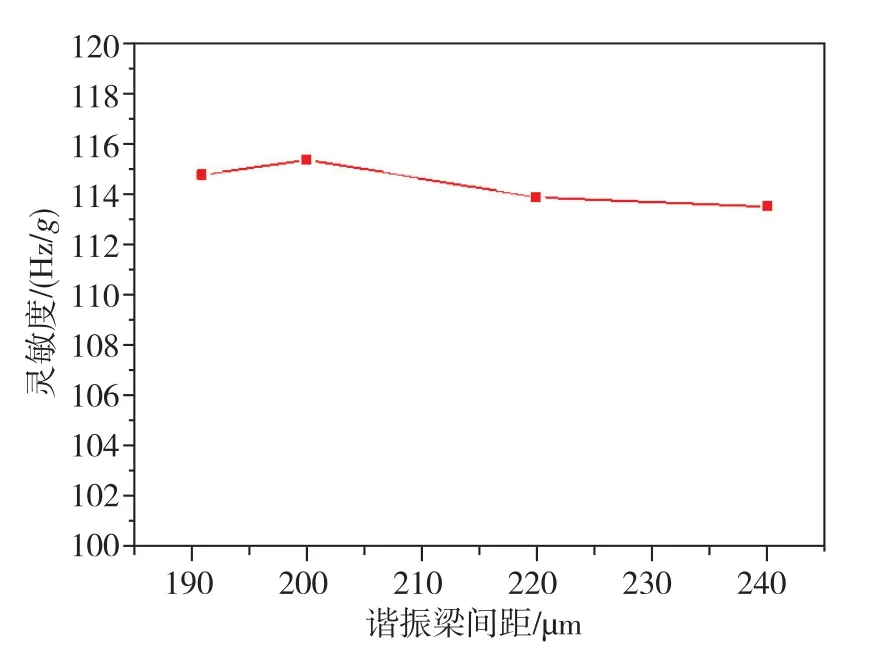
圖11 諧振梁間距與加速度靈敏度的關系Fig.11 Relationship between resonant beam spacing and acceleration sensitivity

由圖11可知,諧振梁間距對加速度靈敏度的影響同樣很小,加速度靈敏度始終保持在114Hz/g～115Hz/g的范圍內。

3 仿真結果與分析

通過對諧振梁關鍵結構的仿真,基于結構改變對諧振頻率的影響比較,梁寬靈敏度為4622.5Hz/μm,梁厚靈敏度為 6.23Hz/μm, 梁長靈敏度為-38.87Hz/μm。根據其靈敏度的絕對值,結構的改變對諧振頻率的影響程度為:梁寬＞梁長＞梁厚。

基于對上述結構施加加速度后的仿真結果,通過得到的擬合曲線與理論推導出的式（6）可得出:梁寬與加速度靈敏度擬合公式為y＝5289.5x－1.747,梁厚與加速度靈敏度擬合公式為y＝7067x－1.053,梁長對加速度靈敏度的影響可忽略不計。梁寬與加速度靈敏度關系近似－2次冪,影響程度略小于諧振梁雙端固定下的理論值；梁厚與加速度靈敏度關系近似－1次冪,影響程度略大于諧振梁雙端固定下的理論值；梁長與加速度靈敏度無關,與式（6）得出的結果一致。因此,在一端固定一端自由并施加加速度載荷的情況下,諧振器的加速度靈敏度會受邊界條件改變的影響,但是影響程度較小。

諧振梁間距對諧振頻率和加速度靈敏度的影響不大,其結構參數主要影響工作諧振頻率與其他干擾諧振頻率的頻率差。除此之外,諧振梁的梁寬、梁厚以及梁長也會影響工作諧振頻率與其他干擾諧振頻率的頻率差。甚至在一定的結構參數與加速度下,會出現工作諧振頻率與干擾諧振頻率數值重合的現象,會對后續閉環控制回路工作諧振頻率的鎖定與追蹤產生一定的影響。

綜上所述,諧振器的高機械靈敏度主要通過調整諧振梁的梁寬與梁厚來實現。針對本文所研究的硅諧振器結構,要實現100Hz/g較高的加速度靈敏度,根據擬合公式,需要滿足在諧振梁厚60μm時諧振梁寬小于9.7μm,或在梁寬10μm時梁厚小于57μm。其他梁寬與梁厚的組合參數可基于MEMS工藝技術情況,根據式（6）初步確定后,通過仿真分析微調結構參數。在確定滿足靈敏度需求的梁寬與梁厚的前提下,可通過調整梁長與兩個諧振梁間距的數值來避免在所需測量的加速度范圍內發生工作諧振頻率與干擾模態諧振頻率重疊的現象。

4 結論

本文通過對一種典型諧振器結構的關鍵結構參數的仿真分析得到了關鍵結構參數對諧振頻率的影響規律,同時驗證了在一端固定一端自由并施加加速度載荷的情況下仿真結果與理論推導結果的一致性與差異點,為后續高機械靈敏度結構設計提供了參考依據。