高速列車通過隧道-橋梁-隧道時車體的氣動效應

鄧鍔 楊偉超 何旭輝 王昂

摘 ? 要：以我國高速鐵路沿線上某座隧道-橋梁-隧道基礎設施為工程背景，基于計算流體力學和多孔介質理論建立了列車-隧道-橋梁-風屏障-空氣三維CFD數值仿真模型，研究了列車運行于隧-橋-隧全過程的氣動荷載變化特性. 針對橫風環境中列車運行于橋隧相連段的過程，從流場角度進一步揭示了風屏障的存在與否對氣動荷載突變效應的影響. 結果表明：1）無風屏障條件下，各節車廂在“由橋至隧”過程的氣動荷載波動幅度是“由隧至橋”過程中相應值的1.03～1.89倍，而風屏障的存在將使兩過程中氣動荷載波動幅度基本相等;2）列車氣動橫向力的變化對風屏障的影響最為敏感，而氣動升力和俯仰力矩的敏感性相對較弱.

關鍵詞：橋隧段;風屏障;高速列車;氣動荷載;突變效應

中圖分類號：U25 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標志碼：A

Abstract：A tunnel-bridge-tunnel （TBT） infrastructure along the high-speed railway in China is taken as the engineering background， based on the theory of CFD and porous media， a 3D CFD numerical simulation model of train-tunnel-bridge-wind barrier-air is established. The aerodynamic load variation characteristic of the train when running on the TBT is studied. Aiming at the process of train running on the bridge-tunnel connection section （BTCS） under crosswind environment， the influence of the existence of wind barrier on the transient change effect of the aerodynamic load is further revealed from the view of the flow field. The results show that： 1） Under the condition without wind barrier， the fluctuation amplitudes of aerodynamic loads of each carriage in the process of 'from bridge to tunnel' are 1.03～1.89 times of the corresponding values in the process of 'from tunnel to bridge'， and the existence of wind barrier makes the fluctuation amplitudes of aerodynamic loads in the two processes basically equal. 2） The change of train aerodynamic side force is most sensitive to the influence of the wind barrier， while the sensitivity of aerodynamic lift force and pitching moment is relatively weak.

Key words：bridge-tunnel section;wind barrier;high-speed train;aerodynamic load;transient change effect

隨著我國西部山區高速鐵路建設的快速發展，高速鐵路沿線中橋隧相連段已成為峽谷兩側最常見的基礎設施場景[1-2]. 如蘭渝線以及滬昆線貴州段，橋梁與隧道占線路總長的比例可達70%～80%. 由于峽谷地形對氣流的特殊作用，當高速列車運行至橋隧相連段或完全運行于橋梁上時常遭遇強橫風[3]. 為同時保證列車運行安全和橋梁結構的穩定性，開孔式風屏障逐漸在該地區橋梁上推廣應用.

近年來，國內外諸多學者圍繞橋上風屏障的防風性能展開一系列研究. 何旭輝[4-5]等通過風洞試驗研究了一種百葉窗型風屏障對車橋系統氣動特性的影響，并針對風屏障參數進行了優化. Xiang等[6]和項超群等[7]研究了不同風屏障高度對運行于橋上的列車氣動荷載的影響，結果表明列車氣動荷載隨風屏障高度增加而減小，風屏障高度為4 m時比沒有設置風屏障時列車各項氣動荷載系數減小40% ～50%. 何瑋等[8]研究了風屏障透風率對橫風下大跨度斜拉橋車-橋耦合振動的影響，結果表明車輛和橋梁的動力響應均隨透風率的增大而增大. Olmos等[9]和郭薇薇等[10]分析了風屏障對車橋系統氣動效應及橋上高速行駛車輛運行安全性的影響. 可見，上述研究主要是針對高速列車完全運行于橋上風屏障區段時的氣動性能及行車安全，并未涉及列車運行過程中基礎設施場景的轉換. 張田等[11]研究發現橫風環境中橋上高速列車進出風屏障時，風載突變對車體橫向振動響應有顯著影響. 事實上，Yang等[12-14]研究發現高速列車在橫風環境下駛入（駛出）隧道時，車身同樣會出現劇烈的氣動突變效應，嚴重威脅列車運行安全. 因此，當高速列車在橫風環境中運行于橋隧相連段時，該區段風屏障的防風性能尤為關鍵.

為此，本文以我國高速鐵路沿線上某座典型的隧道-橋梁-隧道基礎設施為工程背景，基于計算流體力學和多孔介質理論建立了列車-隧道-橋梁-風屏障-空氣三維CFD數值仿真模型;然后以列車運行于該設施全過程的瞬態氣動荷載系數為對象，研究了其變化特性;最后針對橫風環境中列車運行于橋隧相連段的過程（由隧道駛入橋梁或由橋梁駛入隧道），從流場角度進一步揭示了風屏障的存在與否對氣動荷載突變效應的影響. 所得結論有望為我國高速列車運行至隧-橋-隧基礎設施時的行車安全指揮進一步提供理論依據.

1 ? 基本理論

1.1 ? 湍流模型

根據本文工況特點可推測：列車周圍流場馬赫數（Ma）小于0.3，雷諾數（Re）大于106. 因此可認為本文所涉及的流體是不可壓縮且處于高度湍流狀態的. 基于此，本文采用RNG k-ε兩方程湍流模型[15-17]來模擬列車周邊流場結構的瞬態演化過程.

1.2 ? 多孔介質參數計算

本文開孔式風屏障采用多孔介質模型進行模擬，即在流體動量方程中增加一個代表動量消耗的源項. 該源項由兩部分組成，即Darcy黏性阻力項和慣性損失項. 對于簡單的均勻多孔介質，動量源項可表達為：

2 ? 數值模型

2.1 ? 幾何模型及邊界條件

列車模型采用我國高速鐵路常用的CRH3型列車. 建模時，對實際列車的幾何模型進行了一定程度的簡化，忽略轉向架、車頂受電弓以及車窗等部件（如圖1所示），采用3節編組，全長約76 m. 橋梁幾何模型采用我國高速鐵路沿線中使用頻率最高的混凝土簡支箱梁，如圖2所示. 橋長159 m，橋面寬12.0 m，高3.05 m. 不考慮橋面軌道結構及橋墩的影響. 列車底部與橋面距離取0.2 m. 風屏障在全橋范圍內設置，厚0.1 m，高3 m，透風率30%. 橋梁兩端分別與2座雙線隧道連接，隧道長均為200 m，凈空面積均為100 m2.

整體計算區域如圖2（a）所示. 車頭鼻尖初始位置（t = 0 s）距隧道1入口約80 m，車速設置為250 km/h. 隧道1兩端外部大氣場屬于半無限空間，采用半柱體模擬. 其中，隧道1入口外端為平坦地面，相應大氣場直徑約38 m，長200 m，無橫風作用，采用Pressure-oulet邊界條件;橋梁區段大氣場直徑約240 m，采用Pressure-far-field邊界條件，橫風風速設置為25 m/s，且垂直于列車運行方向. 隧道2出口處也采用Pressure-oulet邊界條件. 列車表面、隧道的壁面、橋梁表面及地面均設置成無滑移壁面邊界（Wall）.

2.2 ? 網格策略及計算

基于ANSYS ICEM，采用六面體結構化網格將整個計算區域劃分為3個區域，即動網格區域、靜網格區域和多孔介質區域，如圖3所示. 其中，靜網格區域保持靜止，動網格區域包含列車及其附近的空氣，運用鋪層法[16-17]實現列車與地面的相對運動. 區域之間的流場數據通過組建Interface對進行傳遞. 考慮到車身周圍流場的附面層效應，在車、橋和風屏障的表面分別設置10層、10層和8層附面層網格，第1層網格厚度設為1 × 10-3 m，相應的y+值接近30. 列車表面的網格尺寸約為0.02～0.05 m. 模型總網格單元數約3 200萬. 將模型導入ANASYS FLUENT進行計算，物理時間步長設為1 × 10-3 s.

3 ? 氣動荷載系數計算

單節車廂5項氣動荷載（即氣動橫向力Fz、氣動升力Fy、傾覆力矩Mx、偏航力矩My和點頭力矩Mz）的計算方法可參照文獻[15]. 相應的無量綱化計算公式如下：

4 ? 模型驗證

4.1 ? 網格獨立性檢查

為檢查網格獨立性，通過改變模型網格尺寸分別建立粗（1 600萬）、中（3 200萬）、細（4 800萬）3種具有不同網格單元數的模型. 以列車運行于平地時各節車廂的最大橫向力（Fz，max）為監測指標，橫風風速為25 m/s，車速為250 km/h. 圖5對比了3個模型的監測指標值. 結果表明，網格單元數為3 200萬的模型與單元數為4 800萬的模型計算結果吻合較好. 因此，采用具有3 200萬網格單元數的模型是合理的.

4.2 ? 結果驗證

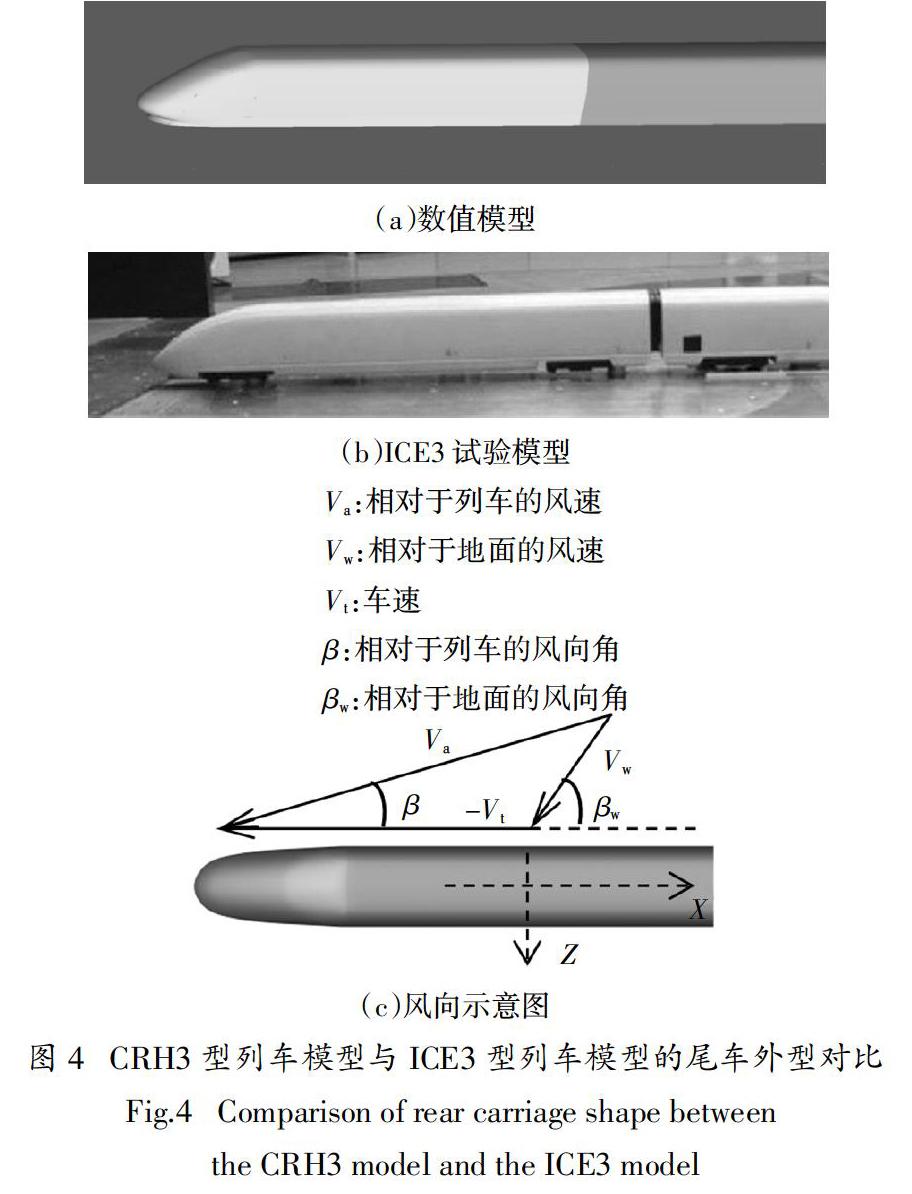
為驗證本文數值模型結果的可靠性，將Schober[18]采用ICE3型（其外型與中國的CRH3型列車高度一致）1 ∶ 15縮尺模型（見圖4）進行風洞試驗所得的尾車氣動荷載數據與本文相應的數值模擬結果進行對比. 為確保本文工況的雷諾數可被該試驗驗證所涉及的雷諾數范圍所覆蓋（本文工況的最大合風速為73.8 m/s，風向角β約為20°），驗證過程中將列車運行速度Vt和風速Va分別設定為0 km/h和78 m/s. 式（6）中參數A 和 h分別取為10 m2和3 m. 最后計算不同β（15°，20°，30°，45° 和 60°）條件下尾車的氣動橫向力系數Cz與偏航力矩系數Cmy，如圖6所示.

由圖6分析可知，本文數值計算結果與Schober的試驗結果變化趨勢基本一致. 除個別數據相差稍大之外，其余的數值計算結果與試驗結果基本吻合，相差保持在10%以內. 因此，可認為本文CFD數值模型及其計算結果是可靠的.

5 ? 結果分析

5.1 ? 氣動荷載

圖7給出了在25 m/s的橫風環境下，列車以速度250 km/h運行于隧道-橋梁-隧道基礎設施過程中，3節車廂的氣動橫向力、升力系數以及傾覆力矩、偏航力矩和俯仰力矩系數時程曲線在有無風屏障條件下的對比. 圖中“出”表示車頭鼻尖駛出隧道1至車尾鼻尖駛入橋梁的過程（t = 4.03～5.13 s）;“進”表示車頭鼻尖駛入隧道2至車尾鼻尖駛離橋梁的過程（t = 6.32～7.42 s）. 根據Deng等[13]的研究，車廂所受的氣動荷載在極短時間內的大幅度波動將顯著提高列車運行的安全風險. 因此，表1給出了對應于圖7的各節車廂分別在“出”和“進”過程中的氣動荷載系數最大波動幅度的對比.

由圖7和表1分析可知：

1）在無風屏障條件下，列車各節車廂的氣動荷載系數在“出”和“進”的過程中均表現出顯著的“脈沖”現象（即瞬間加載和卸載，這一現象與文獻[13]和[14]中所報道的類似）. 說明高速列車在橫風環境下運行于隧道-橋梁-隧道基礎設施時，若橋上沒有設置風屏障，過程“出”和“進”的運行安全風險將顯著高于其他時段.

2）在有風屏障條件下，列車各節車廂的氣動荷載系數在“出”和“進”的過程中的波動幅度均出現顯著下降. 以頭車為例，橫向力、升力、傾覆力矩、偏航力矩和俯仰力矩系數波動幅度在“出”過程中分別下降了86%、82%、80%、59%和36%;在“進”過程中分別下降了87%、83%、83%、61%和61%.

3）無論在“出”或“進”的過程中，風屏障條件下，各節車廂的橫向力波動幅度下降率相對于其余4項氣動荷載均是最為突出的（如，頭車、中間車和尾車在“出”過程中分別高達86%、95%和87%;在“進”過程中分別高達87%、95%和89%）. 中間車的氣動升力系數以及3節車廂的俯仰力矩波動幅度下降率相對較小. 說明運行于橋隧相連段時的列車氣動橫向力的變化對風屏障的影響最為敏感，而俯仰力矩的敏感性相對較弱.

4）在無風屏障條件下，列車各節車廂在“進”過程的氣動荷載波動幅度大于“出”過程的相應值. 用比值“進/出”來量化它們之間的差異可知：頭車、中間車和尾車在“進”過程的氣動橫向力、升力、傾覆力矩、偏航力矩和俯仰力矩的波動幅度分別是“出”過程中相應值的1.03、1.06、1.20、1.03和1.64倍，1.03、1.22、1.00、1.04和1.89倍以及1.16、1.50、1.00、1.03和1.88倍. 而在有風屏障的條件下，列車各節車廂的“進/出”值基本為1. 說明風屏障的存在，將明顯削弱“列車各節車廂在‘進過程的氣動荷載波動幅度大于‘出過程的相應值”這一特征.

5.2 ? 由隧到橋過程的流場及壓力

本節將從流場角度進一步揭示列車在25 m/s橫風環境中由隧道1駛入橋梁過程中氣動荷載突變現象以及風屏障對氣動荷載突變的影響機制. 圖8以軌道頂面上方1.5 m高度處（Y = 1.5 m）的水平面為例，分別給出了有無風屏障條件下列車以速度250 km/h由隧道1駛入橋梁過程中周圍流場變化. 圖9給出了對應過程的車身表面壓力系數分布. 圖中（a）表示車頭鼻尖抵達隧道1出口的時刻（即t = 4.03 s）;（b）（t = 4.40 s）、（c）（t = 4.76 s）和（d）（t = 5.13 s）分別表示頭車、中間車和尾車完全駛出隧道1的時刻.

由圖8和圖9分析可知：

1）無論風屏障的有無，對于隧道內部分車體，其周圍流場結構和車身壓力分布在不同的時刻均表現出相似的特征. 即：車身兩側氣流方向與列車運行方向相反，向車尾鼻尖處匯集;車身兩側壓力基本對稱，且均表現為負壓，壓力值大小也基本相等. 說明橋上風屏障對隧道1內的流場和壓力變化基本沒有影響.

2）對橋上部分車體，在無風屏障條件下，車身背風側在橫風和列車風聯合作用下逐步形成縱向喇叭狀渦流，渦流區對應為負壓區，相應的背風側車體表面也受到沿縱向（與運行方向相反）遞增的負壓（如圖9（c）和（d）中85～120 m區段）;對應的迎風側平直車身表面則在橫風的正面擠壓作用下受沿縱向均勻分布的正壓（壓力系數保持在0.1左右）;車身兩側壓差在車頭鼻尖處最為顯著（最大正壓系數達0.4，最大負壓系數達-0.6）. 在有風屏障條件下，橋上部分車體背風側不再出現喇叭狀縱向渦流;部分流線透過兩側風屏障，在車身背風側匯集并流向前方;除車頭鼻尖前方區域的空氣由于受到擠壓而呈現正壓之外，車身兩側在不同時刻均受基本對稱的負壓（如圖9（b）（c）（d））.

綜上所述，列車由隧道1駛入橋梁過程中，當存在風屏障時，橋上部分車體周圍原有的流場結構特征發生改變，兩側所受負壓均勻且基本對稱，從而導致各節車廂氣動荷載在“出”過程中波動幅度顯著減小;又因風屏障主要引起車身兩側壓差的改變，因此橫向力的變化對風屏障的影響最為敏感.

5.3 ? 由橋到隧過程的流場及壓力

圖10給出了有無風屏障條件下列車以速度250 km/h由橋梁駛入隧道2過程中周圍流場變化. 圖11給出了對應過程的車身表面壓力系數分布. 圖中（a）表示車頭鼻尖抵達隧道2入口的時刻（即t=6.32 s）;（b）（t=6.69 s）、（c）（t=7.05 s）和（d）（t=7.42 s）分別表示頭車、中間車和尾車完全駛入隧道2的時刻.

由圖10和圖11分析可知：

1）橋上風屏障對隧道2內車體周圍的流場以及車身壓力變化仍基本無影響. 具體表現為：無論風屏障的有無，車頭鼻尖處流場均呈現出源流特性，部分氣流沿車身與隧道2之間的空隙于隧道入口處噴出，形成噴射流;隧道內車身兩側壓力沿縱向分布均勻，壓力值基本相等.

2）對于橋上部分車體，在無風屏障條件下，附著于車身背風側的縱向喇叭狀渦流在噴射流抑制作用下終止于隧道2入口處;尚存部分渦流的原有結構在噴射流的干擾下也發生了一定程度的改變，從而導致背風側車身表面負壓增大（如圖11（b）（c）所示）;而迎風側的噴射流由于與橫風聯合作用產生了豎向渦流而消散于隧道2入口處（如圖10（b1）（c1）（d1）所示），故橋上迎風側平直車身表面的正壓系數仍保持在0.1左右. 說明無風屏障條件下，列車各節車廂在“進”過程的氣動荷載波動幅度大于“出”過程的相應值的主要原因可能是列車駛入隧道2時產生的噴射流對背風側縱向渦流的干擾作用.

3）在有風屏障條件下，橫風對于風屏障內側車身兩側的流場結構的干擾明顯減弱. 因此橋上部分車身兩側壓力分布在不同時刻仍保持基本對稱，從而導致各節車廂氣動荷載在“進”過程中波動幅度顯著減小.

6 ? 結 ? 論

1）列車在25 m/s橫風環境中以車速250 km/h運行于橋隧相連段時，無風屏障條件下各節車廂的氣動荷載均表現出顯著的“脈沖”現象;若橋上設置高3 m、透風率為30%的風屏障，相應的各項氣動荷載突變幅度將減少36%～95%.

2）由于風屏障主要引起車身兩側壓差的改變，運行于橋隧相連段時的列車氣動橫向力的變化對風屏障的影響最為敏感，而氣動升力和俯仰力矩的敏感性相對較弱.

3）無風屏障條件下，由于列車駛入隧道時引發的噴射流對列車背風側縱向渦流有干擾作用，各節車廂在“由橋至隧”過程的氣動荷載波動幅度是“由隧至橋”過程中相應值的1.03～1.89倍;若橋上設置風屏障，兩過程中氣動荷載波動幅度基本相等.

參考文獻

[1] ? ?李冬生，馬志富，許占良，等. 長昆線橋隧相連設計研究[J]. 鐵道工程學報，2011，28（12）：69—73.

LI D S，MA Z F，XU Z L，et al. Design and research of bridge-tunnel joint technology on Changsha-Kunming passenger dedicated line[J]. Journal of Railway Engineering Society，2011，28（12）：69—73. （In Chinese）

[2] ? ?韓艷，劉葉，黃靜文，等. 考慮車橋間氣動干擾的橋上車輛行駛安全性分析[J]. 湖南大學學報（自然科學版），2019，46（7）：76—85.

HAN Y，LIU Y，HUANG J W，et al. Traffic safety analysis of vehicles on a bridge considering the aerodynamic interference between vehicles and bridge[J]. Journal of Hunan University （Natural Sciences），2019，46（7）：76—85. （In Chinese）

[3] ? ?LI Y L，HU P，XU X Y，et al. Wind characteristics at bridge site in a deep-cutting gorge by wind tunnel test[J]. Journal of Wind Engineering and Industrial Aerodynamics，2017，160：30—46.

[4] ? HE X H，FANG D X，LI H，et al. Parameter optimization for improved aerodynamic performance of louver-type wind barrier for train-bridge system[J]. Journal of Central South University，2019，26（1）：229—240.

[5] ? ?周蕾，何旭輝，陳爭衛，等. 風屏障對橋梁及車橋系統氣動特性影響的數值研究[J]. 中南大學學報（自然科學版），2018，49（7）：1742—1752.

ZHOU L，HE X H，CHEN Z W，et al. Numerical study of effect of wind barrier on aerodynamic of bridge and train-bridge system[J]. Journal of Central South University （Science and Technology），2018，49（7）：1742—1752. （In Chinese）

[6] ? ?XIANG H Y，LI Y L，CHEN S R，et al. Wind loads of moving vehicle on bridge with solid wind barrier[J]. Engineering Structures，2018，156：188—196.

[7] ? ?項超群，郭文華，陳濤，等. 風屏障對橋上高速列車氣動性能影響的數值研究[J]. 中國鐵道科學，2014，35（5）：113—120.

XIANG C Q，GUO W H，CHEN T，et al. Numerical study on effect of wind barriers on aerodynamic performance of high-speed train on bridge[J]. China Railway Science，2014，35（5）：113—120. （In Chinese）

[8] ? ?何瑋，郭向榮，鄒云峰，等. 風屏障透風率對側風下大跨度斜拉橋車-橋耦合振動的影響[J]. 中南大學學報（自然科學版），2016，47（5）：1715—1721.

HE W，GUO X R，ZOU Y F，et al. Effect of wind barrier porosity on coupled vibration of train-bridge system for long-span cable-stayed bridge in crosswind[J]. Journal of Central South University （Science and Technology），2016，47（5）：1715—1721.（In Chinese）

[9] ? ?OLMOS J M，ASTIZ M ？魣. Improvement of the lateral dynamic response of a high pier viaduct under turbulent wind during the high-speed train travel[J]. Engineering Structures，2018，165：368—385.

[10] ?郭薇薇，夏禾，張田. 橋梁風屏障的氣動效應及其對高速列車運行安全的影響分析[J]. 工程力學，2015，32（8）：112—119.

GUO W W，XIA H，ZHANG T. Analysis on aerodynamic effects of bridge wind barrier and its influence on running safety of a high-speed train[J]. Engineering Mechanics，2015，32（8）：112—119. （In Chinese）

[11] ?張田，夏禾，郭薇薇. 風屏障導致的風載突變對列車運行安全的影響研究[J]. 振動工程學報，2015，28（1）：122—129.

ZHANG T，XIA H，GUO W W. Running safety analysis of the train considering sudden change of wind load induced by wind barrier[J]. Journal of Vibration Engineering， 2015， 28（1）： 122—129. （In Chinese）

[12] ?YANG W C，DENG E，LEI M F，et al. Flow structure and aerodynamic behavior evolution during train entering tunnel with entrance in crosswind[J]. Journal of Wind Engineering and Industrial Aerodynamics，2018，175：229—243.

[13] ?DENG E，YANG W C，LEI M F，et al. Aerodynamic loads and traffic safety of high-speed trains when passing through two windproof facilities under crosswind：a comparative study[J]. Engineering Structures，2019，188：320—339.

[14] ?YANG W C，DENG E，LEI M F，et al. Transient aerodynamic performance of high-speed trains when passing through two windproof facilities under crosswinds：a comparative study[J]. Engineering Structures，2019，188：729—744.

[15] ?DENG E，YANG W C，DENG L，et al. Time-resolved aerodynamic loads on high-speed trains during running on a tunnel-bridge-tunnel infrastructure under crosswind[J]. Engineering Applications of Computational Fluid Mechanics，2020，14（1）：202—221.

[16] ?鄧鍔，楊偉超，尹榮申，等. 橫風下高速列車駛入隧道時瞬態氣動性能研究[J]. 湖南大學學報（自然科學版），2019，46（9）：69—78.

DENG E，YANG W C，YIN R S，et al. Study on transient aerodynamic performance of high-speed trains when entering into tunnel under crosswinds[J]. Journal of Hunan University （Natural Sciences），2019，46（9）：69—78. （In Chinese）

[17] ?鄧鍔，楊偉超，張平平. 橫風下高速列車突入隧道時氣動荷載沖擊效應[J]. 華南理工大學學報（自然科學版），2019，47（10）：130—138.

DENG E，YANG W C，ZHANG P P. Impact effect of aerodynamic loads on high-speed trains when entering into tunnel under crosswinds[J]. Journal of South China University of Technology （Natural Science Edition），2019，47（10）：130—138. （In Chinese）

[18] SCHOBER M，WEISE M，ORELLANO A，et al. Wind tunnel investigation of an ICE 3 endcar on three standard ground scenarios[J]. Journal of Wind Engineering and Industrial Aerodynamics，2010，98（6/7）：345—352.