基于住戶差異性的住宅建筑在室行為預測模型

俞準 劉竹清 李郡 周亞蘋 黃余建 張國強

摘 ? 要：現有住宅建筑在室行為預測模型缺乏對住戶差異性的合理考慮，導致模型往往存在整體預測精度不高和適用性受限等問題. 針對這一問題，提出一種考慮住戶差異性的馬爾可夫鏈在室狀態預測模型. 該模型首先通過Spearman相關性分析確定了不同影響因素（即特征參數）與住戶總在室時長的相關性，將相關系數作為特征參數權值并結合聚類分析對住戶群體進行分類. 在此基礎上采用馬爾可夫鏈模型對住戶在室狀態進行預測. 為評估所建立預測模型的性能，以英國TUS（Time Use Survey）數據庫為例，將改進模型與傳統馬爾可夫鏈模型進行對比分析. 結果表明，該方法能夠綜合考慮不同住戶特征參數及其對在室行為的影響，對住戶進行合理的分類，與傳統馬爾可夫模型相比，所建預測模型顯著提升了整體性能，平均絕對誤差和均方根誤差分別減小了20.57%和15.35%.

關鍵詞：在室行為;住戶差異;相關性分析;聚類分析;馬爾可夫鏈模型

中圖分類號：T111.1 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標志碼：A

Abstract：Existing occupancy prediction models for residential buildings often lack the reasonable consideration of resident diversity， which generally results in poor prediction accuracy and limited applicability. To address this issue， this study proposes a Resident-differentiated， Markov Chain Occupancy Prediction Model with Cluster （RMCPMC） analysis ?to fully consider the resident diversity so as to improve the model predictive performance. First， Spearman correlation analysis is employed to identify the correlation between different influencing factors （i.e. resident characteristics） and total occupancy duration. The identified correlation coefficients are used as the weights for corresponding factors， and cluster analysis is subsequently performed to classify residents into different groups. Finally， RMCPMC models are established for obtained clusters to predict the occupancy pattern. To validate the performance of the proposed model， it is applied to the UK Time Use Survey （TUS） dataset and its performance is compared with the conventional Markov Chain（MC） model. Compared with the conventional MC model， the Mean Absolute Error and the Root Mean Square Error of the prediction accuracy decrease by 20.57% and 15.35%， respectively. The results indicate a significant improvement in model prediction accuracy through reasonably considering resident diversity and their impacts on occupancy patterns.

Key words：occupancy;resident diversity;correlation analysis;cluster analysis;Markov chain model

建筑在室行為是影響建筑能耗的主要因素之一[1]. 就住宅建筑而言，研究表明對其住戶的在室行為，尤其是在室狀態（即居民是否在室），進行合理定量描述和準確長期預測，是提升建筑能耗預測和模擬精度的有效手段[2]. 現有住宅建筑在室狀態預測模型主要包括統計概率模型、數據挖掘模型、馬爾可夫鏈（Markov Chain，MC）模型和Agent-based模型，其中應用最為廣泛的是馬爾可夫鏈模型[3]，該模型考慮了在室狀態在時間上的關聯性并能在一定程度上刻畫建筑住戶行為的隨機性. 例如，Richardson等人[4]基于英國TUS數據庫，分別針對工作日及非工作日建立MC模型以預測住戶在室狀態. 結果表明該方法可以較好地預測在室狀態，但其局限性也較為明顯，主要體現在該方法是對數據庫中所有住戶進行統一預測，忽略了不同住戶之間的差異性. 考慮到不同特征住戶的在室規律有所不同，該方法必然導致模型預測性能下降. 對此，有學者在對住戶進行分類的基礎上進行在室狀態預測. 例如，Flett等人[5]首先選取部分住戶特征參數對英國住宅進行分類，然后對不同類住戶在室狀態進行分別預測. 該方法可在有效降低計算量的同時提高模擬精度，但仍存在明顯的局限性：一是所選取的住戶特征參數受研究者自身經驗和主觀因素影響，容易忽略部分與在室行為相關的重要因素;二是沒有考慮不同因素對住戶在室行為的影響程度大小，限制了模型預測性能的提升. 此外，部分學者嘗試采用無監督聚類分析方法從住戶在室狀態信息中直接獲取不同住戶群體[6]，再對不同群體住戶在室狀態進行預測. 該方法可保證同一住戶群體具有相似的在室作息規律，從而提升了模型預測性能，但由此獲取的住戶群體其社會經濟背景等特征可能具有顯著差異，導致在實際應用中對某一住戶進行能耗模擬時難以確定該住戶屬于哪類群體，從而限制了該方法的實用性.

針對上述問題，本文通過引入Spearman相關性分析及聚類分析對馬爾可夫鏈模型進行改進，提出一種基于住戶差異性的馬爾可夫鏈在室狀態預測模型（Resident-differentiated，Markov Chain Occupancy Prediction Model with Cluster analysis，RMCPMC）. 該模型綜合考慮了不同特征參數對住戶在室行為的影響差異，對住戶進行合理的分類，在此基礎上進一步建立在室狀態預測模型. 本研究采用英國2000年TUS數據庫對模型結果進行驗證，并與傳統馬爾可夫鏈模型進行了對比分析.

1 ? 在室狀態預測模型

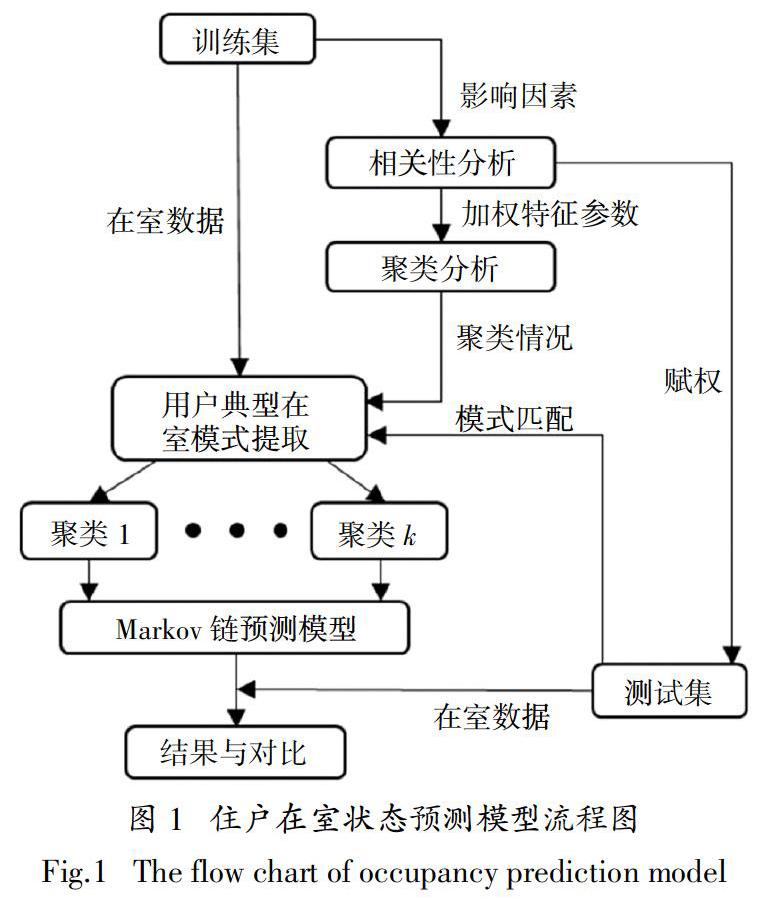
本文提出的基于相關性分析和聚類分析的住戶在室狀態預測模型流程如圖1所示.

由圖1可知，本研究所提出的模型主要包括以下步驟：

1）數據預處理. ?對數據進行清理、篩選和轉換，并通過隨機抽樣選取80%數據作為訓練集，20%數據作為測試集[7].

2）特征參數選取及賦權. 通過Spearman相關性分析，計算不同特征參數與住戶總在室時長之間的相關系數，在此基礎上選取合適的特征參數，并將相關性系數作為權值賦予各特征參數.

3）典型住戶在室狀態模式提取. 將賦權后的特征參數作為對象特征，采用聚類分析將住戶劃分成若干類.

4）預測模型建立. 確定各類住戶初始時刻在室狀態概率和狀態轉移概率矩陣，以分別建立馬爾可夫鏈預測模型.

5）模型驗證. 對測試集住戶進行在室模式匹配（即所屬聚類類別），并采用各馬爾可夫鏈模型分別進行預測，將預測結果與實際在室狀態數據進行對比分析.

1.1 ? 數據預處理

本文對原始數據的預處理過程主要包括數據清理、數據轉換和無量綱化處理.

1）數據清理：由于不同因素影響（如調查對象漏填等問題），數據庫存在部分住戶數據不完整的情況. 為避免缺失數據影響模型結果，本文剔除該部分數據.

2）數據轉換：數據庫中所測參數的類型包括數值型（如住戶年齡）和分類型（如住戶性別）. 不同類型的數據難以直接進行對比分析，因此本文將分類型參數轉換為數值型參數，如住戶性別為“男”則轉化成數值1，反之則為2.

3）無量綱化處理：在應用過程中，取值范圍小的參數易受取值范圍大的參數影響而被忽略其重要性. 為此，本文對參數進行無量綱化處理，將不同參數的取值范圍轉化為相同區間，如[0，1][8].

1.2 ? Spearman相關性分析

由于住戶不同特征因素對其在室行為的影響程度不同，有必要對其相關性進行分析，以確定不同影響因素對住戶在室狀態的影響程度. 本文采用Spearman相關性分析確定不同特征參數與住戶總在室時長的關聯程度. Spearman相關性分析是衡量2個變量的依賴性的統計方法，它利用單調方程評價2個統計變量的相關性. 其中相關系數用符號ρ表示，計算公式如（1）所示[9].

1.3 ?聚類分析

聚類分析是一種根據研究對象相似性將數據集劃分為若干類或簇的過程，目的是保證“類內相似性和類間排他性”[10]. 本文選用劃分聚類分析中k-means算法對加權特征參數進行聚類分析以得到不同住戶群體，其核心思想為指定初始聚類類別及質心，并重復迭代直至算法收斂. 其最佳聚類數k可通過Calinski-Harabasz（CH）指標和Davies- Bouldin（DB）指標確定. 2指標包含對類內相似度與類間分離度的計算，CH指標越大而DB指標越小，則類內相似度和類間分散度越高，說明聚類效果更優. 本文采用開源數據挖掘軟件RapidMiner[11]進行聚類分析，該軟件是一個具有豐富數據挖掘分析和算法功能的開源軟件，通過將不同功能的算子連接形成流程來實現其功能，簡單易學且具有可視化特性.

1.4 ? 馬爾可夫鏈模型

該模型可通過初始在室概率p0和狀態轉移概率矩陣（Transition Probability Matrices，TPM）這兩個參數進行描述. 將該模型應用于住戶在室行為預測時，TPM的大小取決于在室狀態數目（文中為“在室”和“離開”2種狀態），如圖2所示. 此外，考慮到在室狀態具有動態變化特征，本文采用隨模擬步長（即10 min）變化的不均勻TPM. 計算p0和TPM公式如下[14]：

在確定模型參數之后，為對在室狀態進行隨機預測，本文基于初始概率和狀態轉移概率矩陣，通過生成0-1之間的隨機數并將其與相應累計概率分布比較推斷出最可能出現的在室狀態.

2 ? 數據庫與模型評價指標

2.1 ? 數據庫簡介

英國國家統計局于2000年在全國范圍內開展了時間利用調查，建立了Time Use Survey（TUS）數據庫[15]，該數據庫以問卷調查的形式收錄了約2萬個住宅住戶單人日志，且對所有月份及星期天數均有涵蓋，其記錄的詳細日常活動信息能夠提供豐富的住戶行為數據. 這些日志主要包含兩部分內容：

1）與住戶日?；顒酉嚓P的影響因素，包含詳細的個人信息（如年齡、性別、民族、職業、收入、住戶與其他住戶的關系等）和住宅信息（住宅類型、家用電器及車輛擁有權、家庭收入等）.

2）住戶24 h（從4：00am到次日3：50am）具體的日?；顒?，包含一天工作日和一天非工作日，該信息是由住戶主動記錄每間隔10 min其主要日?；顒?、次要日?；顒印⑾鄳恢眉笆欠裼信阃藛T等.

2.2 ? 模型評價

為評估模型的整體性能，本文采用平均絕對誤差（Mean Absolute Error，MAE）和均方根誤差（Root Mean Square Error，RMSE）兩個指標對模型預測精度進行評價. MAE和RMSE反映預測在室狀態概率的整體誤差，計算公式如下：

3 ? 結果與討論

3.1 ? 數據預處理結果

對TUS數據清理后共有12 166個住戶日志數據完整且滿足研究需求，本文選取這部分數據作為研究樣本，并從樣本中包含的日?；顒臃诸愔型茢喑鲈谑仪闆r，其具體信息見表1. 此外，從數據庫中選取了12類可能對住戶在室行為產生影響的因素，具體分類及內容見表2，其中表2中的分類數值均根據其相應順序轉為有序數值，例如，工作狀態共計4種，依次編碼為1～4.

3.2 ? 相關性分析

本文以住戶總在室時長為目標函數，對影響因素進行相關性分析，結果見表3. 由表3可知，在12個影響因素中，工作狀態、身份信息、經濟活躍情況和年齡與住戶的總在室時長正相關系數較大，這意味著住戶的這四類因素與住戶在室持續時長具有顯著相關性. 在分析和預測住宅建筑住戶在室模式時，應重點考察這四種影響因素. 此外，住戶住宅類型以及生活狀況與總在室時長的相關性幾乎為零，這表明二者對在室行為的影響可忽略不計. 因此在后續研究中將這兩個因素剔除，最終選取10個影響因素作為聚類特征參數，并根據相關性系數為各特征參數賦予相應權值.

3.3 ? 住戶典型在室模式

在得到相關系數后，應以賦權特征參數為分類指標對訓練集數據進行聚類分析. 針對不同聚類類別數目（本文設定范圍為2～10），分別計算CH和DB指標，結果見表4. 由表4可知，在k=2時，CH指標最大，DB指標最小，即在保證類內相似最高的情況下類與類之間的距離最遠，聚類效果最優. 因此，本文將樣本住戶分為2類進行研究.

表5為對賦權特征參數進行聚類后，2個聚類的聚類中心（即每個特征參數的平均值）、住戶數量及占比情況. 圖3給出了4個重要特征參數在這2個聚類的詳細分布情況. 結合表5和圖3可看出，第1類住戶的工作狀態、身份信息、經濟活躍和年齡均為最大，這表明該聚類多為不在工作且不在學校、退休、經濟狀態不活躍、年齡較大的人員;第2類住戶多為處于工作狀態、擁有全職工作、經濟狀態活躍、年齡較小的人員.

由上述結果可看出兩類住戶具有明顯不同的特征，為進一步分析不同住戶特征對在室行為模式的影響，圖4給出了兩類住戶的在室狀態概率分布圖. 從圖中可知，兩類住戶的在室模式存在顯著差異. 例如，在8：00—18：00時間段，第2類住戶不在室概率明顯高于第1類住戶，其主要原因是第2類住戶大部分為年齡相對較小的全職工作人員，白天通常處于外出工作狀態;相反，對于第1類住戶（年齡較大的退休或無工作住戶），其主要日常活動為個人護理、休閑娛樂等室內活動，外出活動時間較短. 由此可知，兩種在室模式與聚類所獲取的住戶特征較為吻合，表明基于住戶典型特征參數能夠合理劃分住戶并識別不同住戶的在室行為模式，使得同一類住戶的在室行為模式更為接近.

3.4 ? 模型預測精度比較

在聚類分析所劃分的兩類住戶的基礎上，本文采用訓練集建立了基于住戶差異性的馬爾可夫鏈在室狀態預測模型（RMCPMC模型）. 為驗證模型的有效性，以測試集樣本住戶加權特征參數與兩聚類中心的歐氏距離為依據評判住戶歸屬典型類別，分別根據所建立的RMCPMC模型進行預測. 經分析測試集中有955名住戶（39.25%）屬于第1類，1 478名住戶（60.75%）屬于第2類. 為保證驗證結果的公平性與合理性，應以數據集樣本數目為模擬次數進行預測[4]. 因此，本文以測試集中各個聚類的樣本數量為模擬次數模擬住戶在室行為.

圖5（a）（b）分別給出了RMCPMC模型和傳統MC模型預測在室概率曲線與實際在室概率曲線對比圖及相應的累計誤差對比圖. 結合兩圖可知，盡管2個模型均能大致刻畫實際在室模式，但RMCPMC模型的累積誤差上升速率明顯小于MC模型. 這意味著RMCPMC模型預測誤差明顯低于傳統MC模型. 其主要原因是傳統的MC模型將所有住戶視為同一群體進行預測分析，忽略了住戶差異對在室模式的影響，導致基于訓練樣本計算的住戶在室狀態轉移概率受個體差異的影響，與驗證樣本中的實際轉移概率偏離較大. 而RMCPMC模型由于通過住戶之間的相似性分別計算模型的轉移概率，考慮了不同住戶的特征差異，使得其預測結果更符合同類住戶的實際在室情況. 值得強調的是，圖5給出的在室概率與累計誤差均為1 d的模擬結果，當將RMCPMC和MC 模型應用于在室行為長期預測時（如預測時長為1年，此時需將第一天的模型輸出作為第二天的模型輸入并不斷推進），由于累積效應，RMCPMC模型預測在室概率誤差和累計誤差較傳統MC模型會有更明顯的降低，從而提高相應住宅建筑能耗預測精度.

表6給出了本文所提出的RMCPMC模型與傳統MC模型的整體預測結果. 從表6中可知，相比于傳統MC模型，本文所提出的預測模型的MAE和RMSE分別減少了20.57%和15.35%. 從總體預測結果來看，模型整體預測性能大幅提升. 這一結果表明，通過合理識別相似的建筑在室行為模式，能夠實現提升在室行為預測精度的目的.

4 ? 結 ? 論

本文主要結論如下：

1）住戶特征差異與建筑在室行為具有較強關聯，因此在研究住戶在室行為時應對住戶不同特征與在室行為進行相關性分析. 就本文所采用的數據庫而言，其中相關性較強的影響因素包括住戶的工作狀態、經濟水平、年齡和身份信息.

2）本文方法能綜合考慮住戶差異性對建筑在室行為的影響，通過合理區分不同建筑住戶特征以識別相應的典型在室模式. 本次研究通過聚類分析獲得2類具有明顯不同特征的住戶：第1類住戶多為不在工作且不在學校、退休、經濟狀態不活躍、年齡較大的人員;第2類住戶多為處于工作狀態、擁有全職工作、經濟狀態活躍、年齡較小的人員. 且兩類住戶在室模式與聚類所獲取住戶特征較吻合.

3）與傳統MC模型相比，RMCPMC模型整體預測精度顯著提升，RMCPMC模型可根據住戶特征參數有效判別住戶所屬類別，獲得更加合理的模型輸入參數，預測結果更符合實際，模型預測誤差MAE和RMSE分別減少了20.57%和15.35%.

本文模型的建立和評估均是以英國2000年TUS數據庫為例，將其應用于我國時應結合我國住宅建筑室內人員特征，從數據采集、模型參數選取和聚類分析參數權重分配等方面進行考慮. 同時，就新建住宅住戶行為預測而言，考慮到其住戶特征難以獲取，應基于其規劃設計信息選擇已有類似住宅并采用相關參數進行預測，在后期業主入住后再收集住戶信息對模型進行校核和修正.

此外，本文研究主要針對建筑住戶在室狀態（即在室和不在室）的預測進行分析和驗證，在此基礎上，未來應進一步細化住戶在室行為（如主動/被動在室狀態、與能耗相關行為等）建立相應預測模型，以獲取住戶更全面且詳細的在室狀態，并將其與能耗預測模型相耦合，達到提高能耗模擬精度的目的.

參考文獻

[1] ? ?LABEODAN T，ZEILER W，BOXEM G，et al. Occupancy measurement in commercial office buildings for demand-driven control applications-A survey and detection system evalua-tion[J]. Energy and Buildings，2015，93：303—314.

[2] ? ?俞準，周亞蘋，李郡，等. 建筑用戶在室行為預測新方法[J]. 湖南大學學報（自然科學版），2019，46（7）：129—134.

YU Z，ZHOU Y P，LI J，et al. A new approach for building occupancy prediction[J]. Journal of Hunan University （Natural Sciences），2019，46（7）：129—134. （In Chinese）

[3] ? ?JIA M D，SRINIVASAN R S，RAHEEM A A. From occupancy to occupant behavior：an analytical survey of data acquisition technologies，modeling methodologies and simulation coupling mechanisms for building energy efficiency[J]. Renewable and Sustainable Energy Reviews，2017，68：525—540.

[4] ? ?RICHARDSON I，THOMSON M，INFIELD D. A high-resolution domestic building occupancy model for energy demand simulations[J]. Energy and Buildings，2008，40（8）：1560—1566.

[5] ? ?FLETT G，KELLY N. An occupant-differentiated，higher-order Markov Chain method for prediction of domestic occupancy[J]. Energy and Buildings，2016，125：219—230.

[6] ? ?AERTS D，MINNEN J，GLORIEUX I，et al. A method for the identification and modelling of realistic domestic occupancy sequences for building energy demand simulations and peer compar-ison[J]. Building and Environment，2014，75：67—78.

[7] ? ?周志華.機器學習[M]. 北京：清華大學出版社，2016：25.

ZHOU Z H. Machine learning[M]. Beijing：Tsinghua University Press，2016：25. （In Chinese）

[8] ? ?李郡，俞準，劉政軒，等. 住宅建筑能耗基準確定及用能評價新方法[J]. 土木建筑與環境工程，2016，38（2）：75—83.

LI J，YU Z，LIU Z X，et al. A method for residential building energy benchmarking and energy use evaluation[J]. Journal of Civil，Architectural & Environmental Engineering，2016，38（2）：75—83. （In Chinese）

[9] ? ?陳功平，王紅. 改進Pearson相關系數的個性化推薦算法[J]. 山東農業大學學報（自然科學版），2016，47（6）：940—944.

CHEN G P，WANG H. A personalized recommendation algorithm on improving Pearson correlation coefficient[J]. Journal of Shandong Agricultural University （Natural Science Edition），2016，47（6）：940—944. （In Chinese）

[10] ?HAN J W，KAMBER M，PEI J. Data mining：concepts and techniques [M]. 3rd ed. Beijing：China Machine Press，2012：448—450.

[11] ?NAIK A，SAMANT L. Correlation review of classification algorithm using data mining tool：WEKA，rapidminer，Tanagra，orange and knime[J]. Procedia Computer Science，2016，85：662—668.

[12] ?FOUTZ R V，GRIMMETT G R，STIRZAKER D R. Probability and random processes[J]. Journal of the American Statistical Association，1993，88（424）：1475.

[13] ?李欣然，陳鴻琳，冷華，等. 中長期電量預測的傅里葉-馬爾科夫修正模型[J]. 湖南大學學報（自然科學版），2016，43（10）：62—69.

LI X R，CHEN H L，LENG H，et al. ?Mid-long term load forecasting model with Fourier series and Markov theory residual error correction[J]. ?Journal of Hunan University （Natural Sciences），2016，43（10）：62—69. （In Chinese）

[14] ?WID？魪N J，W？魨CKELG？RD E. A high-resolution stochastic model of domestic activity patterns and electricity demand[J]. ?Applied Energy，2010，87（6）：1880—1892.

[15] ?Ipsos-RSL and Office for National Statistics. United Kingdom Time Use Survey，2000. [EB/OL]. [2003-09]. https：//census.ukdataservice.ac.uk/.