直升機懸停狀態(tài)下的振動計算

姚 頌,芮筱亭,王景弘

(南京理工大學 能源與動力工程學院，南京 210094)

振動是影響直升機發(fā)展的主要問題之一.對于大多數(shù)現(xiàn)代直升機而言，機動能力和最大前進速度受到過度振動的限制.發(fā)動機、變速箱、尾槳和旋翼質(zhì)量不平衡都是振動激勵源.然而直升機振動的主要來源是主旋翼.振動對直升機操作的幾乎所有方面都是有害的，包括飛行員疲勞和結(jié)構(gòu)完整性；降低電子設(shè)備的可靠性和操作準確度；影響相機和測量設(shè)備等機器的精度.旋翼槳葉可以模擬為旋轉(zhuǎn)梁[1]，由于彈性變形和剛體運動的耦合，旋轉(zhuǎn)梁的振動特性與非旋轉(zhuǎn)梁的振動特性有很大差異[2].沿著梁長度變化的離心力改變了梁的整體剛度(應(yīng)力剛化效應(yīng))，使固有頻率和模態(tài)發(fā)生變化[3].眾多研究人員針對不同的課題，采用不同的方法研究了旋轉(zhuǎn)梁的動態(tài)特性.例如Southwell原理、積分矩陣法、Rayleigh Ritz法[4]、Galerkin法[5]和擾動法，以及動態(tài)剛度法，這涉及到冪級數(shù)解及使用Frobenius方法計算相應(yīng)微分方程的解[6].傳統(tǒng)的有限元法(Conventional finite element method,CFEM)[7]已被用于許多分析旋翼固有頻率的問題.一種基于低自由度模型的譜有限元法(Spectral finite element method，SFEM)[8]被用于分析旋轉(zhuǎn)錐形梁的運動特性.傳遞矩陣法用于非旋轉(zhuǎn)錐形梁[9]和帶裂紋的旋轉(zhuǎn)梁[10]的自由振動計算.

有限元法和多體系統(tǒng)動力學是武器系統(tǒng)動力學的重要基礎(chǔ).然而，使用這些方法對多剛?cè)狍w耦合的復雜武器系統(tǒng)的振動特性計算可能帶來很大的計算量和由計算不良條件引起的計算奇點.多體系統(tǒng)傳遞矩陣方法(MSTMM)[11-13]可以避免復雜線性多系統(tǒng)特征值問題的計算錯誤，因為系統(tǒng)總矩陣階次較低，顯著提高了振動特性的計算速度[14].本文基于MSTMM，建立了耦合直升機四葉片旋翼/機身的多體系統(tǒng)動力學模型.推導出整體傳遞方程，并模擬了旋翼振動特性.為了證明所提出方案的準確性，與商業(yè)軟件ANSYS Workbench仿真結(jié)果進行比較.

1 建模與傳遞矩陣推導

1.1 直升機拓撲模型

圖1中所示的典型直升機可以建模為多剛性-柔性耦合系統(tǒng)，直升機主要分為旋翼系統(tǒng)、機身和機尾3個部分.

圖1 典型直升機模型

拓撲結(jié)構(gòu)如圖2所示，四槳葉/機身耦合系統(tǒng)的動力學模型在空間內(nèi)振動.全局慣性系oxyz用于描述系統(tǒng)運動.本文將直升機模型簡化為8個元件，分別是4個旋轉(zhuǎn)Euler-Bernoulli梁組成的無鉸接柔性槳葉、槳轂、傳動軸、機身和尾梁8個部分.元件編號1至4號是槳葉，考慮其在揮舞方向、擺振方向及扭轉(zhuǎn)方向的振動，槳葉通過柔性連接到5號元件槳轂，槳轂處理為一個空間剛體，槳轂連接至元件6傳動軸，傳動軸處理為一根圍繞中心軸旋轉(zhuǎn)的梁，傳動軸與元件7機身相連，機身處理為一個剛體，機身與元件8尾梁為剛性連接.旋翼與傳動軸以同一轉(zhuǎn)速旋轉(zhuǎn)，旋轉(zhuǎn)角速度為Ω.

圖2 直升機拓撲模型

1.2 系統(tǒng)總傳遞矩陣的推導

遞矩陣法使用狀態(tài)矢量描述力學系統(tǒng)中任一點的力學狀態(tài)，坐標系方向及符號約定如圖3所示，狀態(tài)矢量是由兩部分元素構(gòu)成的一個列陣，一是該點狀態(tài)變量的位移及角位移(x,y,z,θx,θy,θz)，二是內(nèi)力及內(nèi)力矩(qx,qy,qz,mx,my,mz).多自由度無阻尼振動系統(tǒng)可由模態(tài)振動疊加而成，某階模態(tài)下固有頻率ωk對應(yīng)的狀態(tài)矢量可以表示為z=Zke-iωkt,Zk為模態(tài)坐標下的狀態(tài)矢量，其狀態(tài)變量為固有頻率ωk對應(yīng)的位移及內(nèi)力的模態(tài)坐標，為了書寫簡潔將上標k省略，即Zi,j=[X,Y,Z,Θx,Θy,Θz,Mx,My,Mz,Qx,Qy,Qz]T，其中i為體元件編號，j為鉸元件編號.

圖3 坐標系及符號約定

系統(tǒng)總傳遞方程由總傳遞方程和幾何方程構(gòu)成，總傳遞方程的狀態(tài)矢量由所有邊界點的狀態(tài)矢量構(gòu)成.主傳遞方程中的每一個系數(shù)矩陣為從相應(yīng)邊界點到系統(tǒng)根的傳遞路徑上所有元件傳遞矩陣的連乘積.幾何方程用來描述同一元件不同輸入點之間的幾何關(guān)系，其系數(shù)矩陣可以在推導主傳遞方程的過程中依據(jù)同一元件不同輸入點之間的幾何關(guān)系自動導出.對于每一個分支，都可以根據(jù)同一個體元件不同輸入點的幾何關(guān)系推導出一組幾何方程，幾何方程的個數(shù)等于系統(tǒng)樹梢個數(shù)減1.幾何方程的系數(shù)矩陣為由從邊界端到分叉體元件的輸入端Ik(k=1,2,…，L)路徑上各個元件的傳遞矩陣的連乘積，再左乘(-Hj,1)(若k=1)，或左乘(Hj,k)(若k=2,…，L).

在線性系統(tǒng)中ZO=UjZI，其中：ZI為輸入點的狀態(tài)矢量，ZO為輸出點狀態(tài)矢量，Uj為元件j的傳遞矩陣，由牛頓力學定律推導得到，總傳遞矩陣Uall為沿傳遞路徑各元件傳遞矩陣依次連乘之積.最終整理可以得到UallZall=0，其中Zall為各邊界點的狀態(tài)矢量和，Uall即為總傳遞矩陣.

如圖2拓撲圖所示，該模型共有4個邊界點，分別為Z1,0,Z2,0,Z3,0,Z4,0,Z8,0,以Z8,0為輸出點，系統(tǒng)的傳遞矩陣推導如下：

Z8,0=U8Z7,8=U8U7Z7,6=U8U7U6Z5,6=

U8U7U6(U5,I1Z5,1+U5,I2Z5,2+

U5,I3Z5,3+U5,I4Z5,4)=U8U7U6(U5,I1U1Z1,0+

U5,I2U2Z2,0+U5,I3U3Z3,0+U5,I4U4Z4,0)=

U8U7U6U5,I1U1Z1,0+U8U7U6U5,I2U2Z2,0+

U8U7U6U5,I3U3Z3,0+U8U7U6U5,I4U4Z4,0,

(1)

或

T8-1Z1,0+T8-2Z2,0+T8-3Z3,0+T8-4Z4,0-Z8,0=0,

(2)

其中：

T8-1=U8U7U6U5,I1U1,T8-2=U8U7U6U5,I2U2,

T8-3=U8U7U6U5,I3U3,T8-4=U8U7U6U5,I4U4.

模型中有一個分叉點，4個分支，所以共有3個幾何方程.第1個幾何方程如下：

-H5,1U1Z1,0+H5,2U2Z2,0=0,

(3)

或

G5-1Z1,0+G5-2Z2,0=0,

(4)

其中：

G5-1=-H5,1U1Z1,0，G5-2=H5,2U2Z2,0.

第2個幾何方程如下：

-H5,1U1Z1,0+H5,3U3Z3,0=0,

(5)

或

G5-1Z1,0+G5-3Z3,0=0,

(6)

其中：

G5-1=-H5,1U1Z1,0,G5-3=H5,3U3Z3,0.

第3個幾何方程如下：

-H5,1U1Z1,0+H5,4U4Z4,0=0,

(7)

或

G5-1Z1,0+G5-4Z4,0=0,

(8)

其中：

G5-1=-H5,1U1Z1,0,G5-4=H5,4U4Z4,0.

聯(lián)立式(2)、(4)、(6)、(8)，可得

Uall|30×60Zall|60×1=0,

(9)

其中：

2 主要元件傳遞矩陣的推導

2.1 旋轉(zhuǎn)梁的傳遞矩陣的推導

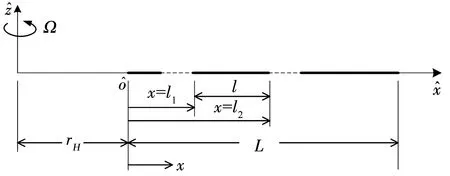
圖4 旋轉(zhuǎn)梁揮舞方向振動的符號約定和坐標系

(10)

式中rH為梁的輸入端距離旋轉(zhuǎn)軸的距離，其中離心力F(x)可以表示為

(11)

(12)

梁的動能T由下式給出：

(13)

Hamilton原理可以表示如下:

(14)

將式(10)、(13)代入式(14)中，可以得到揮舞方向振動的運動微分方程：

(15)

將式(15)中位移改寫為譜坐標形式，即z(x,t)=Z(x)eiωt，并代入式(11)、(12)，化簡方程可得

ZIV(x)-(0.5C1+rHC1x+C2)Z″(x)+
C1(rH+x)Z′(x)+C3Z(x)=0,

(16)

其中:

方程(16)的根是使用冪級數(shù)中的Frobenius方法計算的，并且可以假設(shè)該微分方程的解如下：

(17)

將式(17)代入式(16)中，可以得到:

(18)

上式也可以寫為如下形式：

C2(k+i+1)(k+i+2)ai+3+C1rH(k+i+1)2ai+2+

[C1(k+i)+0.5C1(k+i-1)(k+i)+C3]ai+1}xk+i.

(19)

代入i=-4到式(19)中，可以發(fā)現(xiàn)只有a1得系數(shù)非零，其他的項都等于0.因此，將i=-4代入式(19)中，發(fā)現(xiàn)a1是最低階非消失系數(shù)，得到k(k-1)(k-2)(k-3)a1=0,其中a1≠0, 那么k只有0，1，2和3這4個根滿足方程k(k-1)(k-2)(k-3)=0，并且a1是任意數(shù)，這里假設(shè)a1=1, 式(19)中的未知系數(shù)的一般形式可以用以下表達:

(20)

分別將i=-3,i=-2,i=-1及i=0代入式(20)中，依次得到:

(21)

從式(19)、(20)可以確定所有未知系數(shù)，對于k=0,1,2,3,微分方程式(19)的解可以用4個獨立線性解的總和乘以任意常數(shù)表示如下:

Z(x)=A1f(x,0)+A2f(x,1)+A3f(x,2)+A4f(x,3),

(22)

式中A=[A1,A2,A3,A4]T是任意常數(shù)，方程(22)中k=0,1,2,3的4個獨立解f(x,k)可以用函數(shù)的形式表示如下:

f(x,0)=a1(0)x0+a3(0)x2+a4(0)x3+a5(0)x4+…,

f(x,1)=a1(1)x1+a3(1)x3+a4(1)x4+a5(1)x5+…,

f(x,2)=a1(2)x2+a3(2)x3+a4(2)x4+a5(2)x5+…,

f(x,3)=a1(3)x3+a3(3)x4+a4(3)x5+a5(3)x6+….

(23)

由材料力學可得旋轉(zhuǎn)梁在此平面內(nèi)的彎矩和剪切力，分別為:

(24)

2rHx-x2)Z′(x)-F0Z′(x).

(25)

在MSTMM中，槳葉揮舞方向z-x平面內(nèi)的邊界條件為[Z,Θy,My,Qz]T，根據(jù)線性關(guān)系可以得到Θy=Z′，聯(lián)立式(24)、(25)，可以寫成如下形式Z(x)=D(x)A.

(26)

其中:

H1=EI[f?(x,0)+γf′(x,0)],

H2=EI[f?(x,1)+γf′(x,1)],

H3=EI[f?(x,2)+γf′(x,2)],

H4=EI[f?(x,3)+γf′(x,3)],

γ=(0.5C1x2+rHC1x+C2).

由式(26)可以得到在x=l1作為輸入端的狀態(tài)適量為ZI=[D(l1)]A，從而這組未知的系數(shù)向量可以表示為A=[D(l1)]-1ZI，那么位于x=l2的輸出端的狀態(tài)矢量為

ZO=[D(l2)]A=[D(l2)][D(l1)]-1ZI=URBZI,

(27)

式中URB=[D(l2)][D(l1)]-1為旋轉(zhuǎn)梁在揮舞平面內(nèi)橫向振動的傳遞矩陣.

同理，在擺振運動平面內(nèi)也以此方法獲得其傳遞矩陣，但在離心力部分略有不同，由于離心力的作用方向分為擺振方向和展向分量，因此運動微分方程為

(28)

非圓截面梁的扭轉(zhuǎn)通過材料力學可以得知微段的扭轉(zhuǎn)角φ與扭矩T的關(guān)系為

(29)

式中:G為剪切模量；h為截面長邊；b為截面短邊；β為矩形截面桿扭轉(zhuǎn)時的因數(shù)，當h/b遠大于10時，β近似等于0.333,It=βhb3.在扭轉(zhuǎn)方向上由于螺槳效應(yīng)的影響，即由離心力Ω引起回復力矩，扭轉(zhuǎn)振動的運動微分方程為

(30)

其中Iα為微段繞扭轉(zhuǎn)軸的轉(zhuǎn)動慣量.

通過求解式(30)這個微分方程，最終可以得到長為x的旋轉(zhuǎn)梁扭轉(zhuǎn)振動的傳遞矩陣如下：

(31)

2.2 傳動軸的傳遞矩陣的推導

圖5 旋轉(zhuǎn)軸模型

(32)

代入模態(tài)坐標u(z,t)=U(z)eiωt和v(z,t)=V(z)eiωt，并引入量綱一的長度ξ=z/L與微分算子D=d/dξ，整理后式(33)變?yōu)?/p>

(33)

對式(33)求解后分別得到U(ξ)和V(ξ)的通解:

(34)

A1-A8與B1-B8是兩組獨立的8個常系數(shù)，其之間的關(guān)系如下：

(A1,A2,A3,A4)=kα(B1,B2,B3,B4),
(A5,A6,A7,A8)=kβ(B5,B6,B7,B8),

(35)

其中：

由式(32)可以得出扭轉(zhuǎn)角，彎矩與剪切力的表達式如下：

(36)

(37)

(38)

將式(34)、(35)分別代入到式(36)～式(38)中，整理后可以得到x=l1處的狀態(tài)矢量為

(39)

式中ZI=[U,V,θx,θy,Mx,My,Sx,Sy]T，以x=l2為輸出端，可以得到：

(40)

(41)

式中US為旋轉(zhuǎn)軸的傳遞矩陣.

3 計算與仿真對比驗證

3.1 旋轉(zhuǎn)梁的固有頻率驗證

為驗證MSTMM計算旋轉(zhuǎn)梁頻率的準確性，分別對轉(zhuǎn)速為0，20，40 rad/s時懸臂梁的頻率計算，使用MATLAB編程計算與Ansys Workbench仿真結(jié)果的前五階頻率對比.梁的參數(shù)分別為，長度L=6 m，橫截面長b=0.5 m，高h=0.04 m，密度ρ=334 kg/m3，彈性模量E=7.1 MPa，剪切模量G=2.730 8 MPa，泊松比μ=0.3. ANSYS Workbench的模型有88 413個節(jié)點，網(wǎng)格單元數(shù)為15 600.

計算結(jié)果與對比見表1，3種轉(zhuǎn)速下前五階頻率結(jié)果誤差較小.取3次相同計算條件下的平均時間，使用MATLAB編程的計算時間為6.3 s，ANSYS Workbench的計算時間是55.9 s.計算速度提高了8.8倍.

表1 懸臂梁在3種轉(zhuǎn)速下MSTMM計算與ANSYS仿真的固有頻率對比

續(xù)表1

3.2 旋轉(zhuǎn)軸的頻率計算結(jié)果驗證

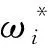
(42)

表2 圓截面懸臂旋轉(zhuǎn)軸的固有頻率(EIxx=EIyy)

3.3 懸停直升機整機頻率計算

為了驗證MSTMM方法計算的準確性，對圖2直升機模型進行驗證計算.直升機各部件的參數(shù)如下，槳葉密度ρ=334 kg/m3，長度L=6 m，橫截面長b=0.5 m，高h=0.04 m，彈性模量E=7.1 MPa，剪切模量G=2.730 8 MPa；槳轂密度ρ=7 850 kg/m3，尺寸為長和寬為0.5 m，高0.3 m；傳動軸密度ρ=7 850 kg/m3，尺寸為直徑0.16 m,，高為1 m，彈性模量E=2.5 MPa，剪切模量G=9.615 4 MPa；機身密度ρ=170 kg/m3，長3 m，寬1.8 m，高1.6 m，質(zhì)心與機身傳動軸連接點在X軸上的投影距離0.4 m；尾梁密度ρ=140 kg/m3，截面高和寬為0.8 m，長為4 m，彈性模量E=2 MPa，剪切模量G=7.692 3 MPa.尾梁末端采用固定約束，旋翼系統(tǒng)的轉(zhuǎn)速為36.651 9 rad/s. ANSYS Workbench模型的節(jié)點數(shù)88 260，16 056個單元. 前12階頻率見表3.

表3 使用MSTMM方法計算旋轉(zhuǎn)狀態(tài)直升機固有頻率與ANSYS仿真結(jié)果對比

計算結(jié)果與仿真結(jié)果基本一致.3次相同計算條件下的平均時間，使用MATLAB編程的計算時間為11.5 s，ANSYS Workbench的計算時間是81.2 s.計算速度提高了7.1倍.由此可以使用MSTMM方法計算無約束條件即懸停狀態(tài)下直升機模型的固有頻率，前8階的計算結(jié)果見表4.

表4 懸停狀態(tài)下直升機模型固有頻率

4 結(jié) 論

1)本文推導了旋轉(zhuǎn)梁在揮舞、擺振和扭轉(zhuǎn)3個自由度的運動方程，得到其傳遞矩陣，算例通過與ANSYS仿真結(jié)果對比，誤差在1.5%以內(nèi)，驗證了結(jié)果的準確性.

2)推導了旋轉(zhuǎn)軸的傳遞矩陣，算例與參考文獻結(jié)果對比，誤差不超過0.15%，驗證了準確性.

3)MSTMM可以快速準確地計算動力學問題.并且相較于傳統(tǒng)動力學軟件Workbench ANSYS，結(jié)果相近，計算時間大大縮短，本文算例計算時間縮短了7倍以上.

4)對直升機旋翼/機身耦合系統(tǒng)驗證計算，與仿真結(jié)果基本一致，并得到了懸停狀態(tài)下的前8階固有頻率，對直升機設(shè)計具有一定參考價值.