二維非遞歸的低成本FIR濾波器設計方法

鐘燕清,閻躍鵬,孟 真,田 易,劉 謀,李繼秀

(1.中國科學院 微電子研究所,北京 100029； 2.中國科學院大學,北京 100049)

FIR數字濾波器為對稱型結構，階數和量化位寬是決定數字濾波器硬件資源的兩個重要因素，通常情況下，階數越高、量化位寬越大，硬件資源消耗越多.考慮到FIR濾波器的參數是固定的，人們引入了固定乘數優化算法進行優化處理[1]，即將乘法分解成加法和移位計算，降低運算復雜度.在已有的數字濾波器的固定乘數優化算法中，加法深度LD(logic depth)和加法器個數LA(logic adder)是衡量算法優劣性的兩個重要指標.降低加法器個數需要盡可能復用系數中的公共項，從而帶來加法深度的增加；降低加法深度則意味著降低公共項的復雜度，帶來加法器LA的增加.LD和LA的結果不僅取決于系數的量化位寬、階數，也取決于用戶的優化方式，是一個綜合性的優化問題.考慮到常系數乘法的加法器個數與系數非零項直接相關，Park等[2-3]提出采用CSD、MSD表示法表示濾波器系數，在后續的算法中得到了廣泛應用.在此基礎上,人們提出了采用遞歸式算法和非遞歸式算法的不同公共項提取思路來降低電路中的加法器消耗.前者[4-9]以BHM[4]、RAG-n[5-6]、HARTLEY[7]和HCUB[8]為代表，采用迭代運算窮舉固定系數的所有公共項，可以達到最優的降低MCM加法器的效果.RAG-n、BHM和HCUB算法均采取圖形啟發式方式進行優化，即先對系數進行排序，以最小的系數為公因子，窮舉各個系數的公因子組合方式，選取代價最小的作為最優解.其中Bull等[4]最早提出采用圖形化的方法來從小到大組合濾波器系數，取得了較好的效果；Dempster等[5]在此基礎上進行了改良，擴展了系數范圍，提出了BHM算法；而RAG-n則更進一步，采用查表法遍歷了所有可能，所以加法器個數LO最少，但是代價是需要預存分解表，算法復雜度最高，運算時間最長，加法深度最高. HCUB算法則是在此基礎上，引入了中間變量算子，降低了算法對分解表的要求，是目前最優的啟發式優化算法. 然而，上述圖形啟發式優化方法均存在算法復雜度高、求解時間隨量化位數增加急劇上升的問題，同時由于采用公共項的多次復用，邏輯深度居高不下，引入大量的路徑延時，對后期電路的設計和綜合非常不友好.非遞歸式[10-16]則以直接提取公共項進行有限次數迭代，具有算法復雜度低、可綜合性好等優點，代表性的有NR-SCSE、HSSE、VSSE算法等.其中Peiro等[14]提出的非遞歸有符號公共項消去算法(Non-recursive signed common sub-expression elimination, NRSCSE)，采用一維搜索頻次最高的公共項的算法，算法復雜度低，邏輯深度低，取得了非常好的同時降低LO和LD的效果.為了達到降低邏輯深度的目的，該算法只啟用包含2個非零項的公共項，具有最低邏輯深度特性. 然而，上述非遞歸式算法均只進行了一維的共同項(單獨的系數矩陣的行公共項或者單獨的列公共項)的提取，并沒有考慮到系數矩陣的二維特性，在加法器個數的指標上整體落后于遞歸算法.

為了達到邏輯深度和加法器個數的雙重優化效果，本文提出了一種新的二維非遞歸優化算法. 其在一維非遞歸式算法的基礎上，對系數矩陣的第2個維度進行公共項提取，從而達到進一步降低加法器個數的效果.仿真結果表明，相比于一維的NRSCSE，本文設計的濾波器優化算法(后文簡稱ONRSCSE)可以降低10%左右的系數加法器數量，具有良好的推廣價值.

1 一維非遞歸算法

數字濾波器的濾波效果是通過輸入信號與濾波系數的卷積運算來實現的，具體來說，輸入信號x進入一個N階的數字FIR濾波器后，需要與N-1個系數進行乘法運算，之后進行累加，得到輸出值.假定N階FIR濾波器的系數由低階到高階分別為：h(0),h(1),…，h(N-1),則有該濾波器的響應為

(1)

式中：x(n)、y(n)分別為濾波器的輸入和輸出.假定濾波器的系數矩陣為H，H=[h0,h1,…,hN-1]，當前輸入為x(n)，則輸出Y=H×X，X=x(n)×[z0,z-1,z-2,z-3]為輸入矢量.

考慮到FIR濾波器的系數對稱性，通常采用優化的轉置式實現，假定FIR為I型濾波器，N為奇數，則實現的濾波器結構如圖1所示.由于其系數對稱性，即h0=hN-1，h1=hN-2，對系數的優化只需要對其前1/2系數h0，h1，…，h(N-1)/2進行即可.

圖1 FIR濾波器的優化轉置結構

傳統的非遞歸優化算法在將系數hi采用CSD法表示后，對各個系數的非零項進行統計，依次提取出現頻率最高的間距相同、符號相同/相反的非零項作為公共項，對系數進行分解，直到系數無法再提取公共項為止，通常為一維搜索算法.以NRSCSE[14]算法為例，其只搜索系數內的任意間距2個非零位公共項，在量化位數為b時，單個系數最多存在2×(b-1)個公共項，邏輯深度最多為「log2b/2?.由于只需要搜索和消去運算，NRSCSE算法復雜度非常低，非常適合于普通濾波器的優化.然而，由于只用到了系數內的冗余項，在系數非零項為單數時必然會出現單個的1/-1不能復用，而導致2n個非零項和2n-1個非零項的優化效果一樣，增加加法器的消耗.以4個系數為例說明此問題：

h(0)=1 288,h(1)=776,h(2)=1 077,

h(3)=1 189.

(2)

將其表示為12 bit的CSD數后，系數如下：

h(0)=0x508=(010100001000)CSD,

h(1)=0x308=(010-100001000)CSD,

h(2)=0x435=(0100010-10101)CSD,

h(3)=0x4a5=(010010100101)CSD.

(3)

采用NRSCSE提取公共項101/10-1后，得到剩余矩陣(后文稱為殘余矩陣)為

(4)

則整體表示法為

(5)

式中:公共項S0=x0?2+x0，S1=x0?2-x0，如圖2中紅色方框內所示.共需要加法器8個，邏輯深度(系數中最大加法器個數+1)為2層.

圖2 濾波器系數的NRSCSE優化示例

考慮到經過系數內的公共項提取后，系數殘余矩陣內還存在冗余信息，如圖2中藍色圓框所示，可以進一步進行優化.

2 二維非遞歸優化算法

二維非遞歸優化算法(Optimized non-recursive signed common sub-expression elimination，ONRSCSE)是行公共項和列公共項提取的結合，是一種典型的非遞歸固定乘數優化方法.其大致思路為：首先采用CSD法表示FIR濾波器的前1/2系數，將系數表示為{-1，0，1}的初始系數矩陣；然后采用行公共項提取的方法依次分解系數矩陣的行系數，直到滿足行分解的終止條件為止；之后對分解后剩余的非0系數矩陣(后文稱為殘余矩陣)進行列公共項分解，直到滿足終止條件為止；最后將系數表示成分解出的行與列公共項的移位與加法組合，完成整個算法優化.

以一維優化為例，本文在一維非遞歸算法的基礎上，對上述殘余矩陣式6進行列公共項的提取，得到列公共項[1 1]T，記為S2=x0+x0[-1]，[-1]表示對系數進行一個單位的延時，則濾波器此部分的輸出為

(6)

整體實現一共需要加法器7個，邏輯深度2層. 因此，相比于一維的NRSCSE算法，本算法(ONRSCSE)增加了列系數的非零項搜索，節省了 1個加法器資源.

不難推算，NRSCSE算法優化的殘余矩陣中非零項越多，列公共項出現次數越多，本算法的優化效果越顯著.

2.1 名詞定義

2.1.1 系數矩陣

由CSD表示后的濾波器系數組成的矩陣，矩陣元素為{-1，0，1}，假定濾波器系數量化位寬為b，階數為n，本算法通常取前1/2系數第0～m階組成系數矩陣(如果n為偶數，m=n/2；如果n為奇數則m=(n-1)/2).系數矩陣記為Hi，下標i代表第i次系數分解，H0為初始化系數矩陣.

2.1.2 殘余矩陣

系數矩陣減去公共項元素后剩余的非0矩陣.

2.2 算法描述

在系數矩陣的基礎上，對公共項進行二維搜索，遵循規則為——先迭代搜索行公共項，再搜索列公共項.

2)對系數矩陣Hi進行行系數分解，方法為統計在整個系數矩陣中出現次數最多的行公共項，將其作為最優公共項；

3)在系數矩陣Hi中消去最優公共項，得到殘余矩陣Hi+1，則Hi可以表示為Hi+1與最優公共項的移位和加法組合；

4)返回步驟2)繼續分解殘余矩陣Hi+1，直到滿足行分解的終止條件——公共項矩陣中最優公共項出現次數小于2為止，進入步驟5).假定此時已經進行了j次迭代，得到了殘余矩陣Hj；

5)對殘余系數矩陣Hj進行列分解，方法為統計在整個系數矩陣中出現次數最多的列公共項，將其作為最優公共項；

6)在系數矩陣Hj中消去最優公共項，得到殘余矩陣Hj+1，則Hj可表示為Hj+1與最優列公共項的移位和加法組合；

7)返回步驟5)繼續分解殘余矩陣Hj+1，直到滿足列分解終止條件為止，進入步驟8)；

8)將濾波器的輸出y表示為所有行、列公共項的移位和累加*輸入的組合.

2.3 算法復雜度分析

3 結果及分析

3.1 實驗數據集

本文采用通用的濾波器設計方法，一共設計了19個不同特性的濾波器，并對其進行不同量化位寬、不同階數的例化，產生了共82個濾波器，此為算法優化的對象.

其中為對比本算法與一維非遞歸算法，采用MATLAB的FDAtool工具產生了12組數字FIR帶通濾波器，階數從37階到649階，并對每組濾波器系數進行了12、16 bit的量化，覆蓋了常用的數字濾波器范圍，此為數據集1.

為對比本算法與遞歸型優化算法，采用Parks-McClellan法設計7種不同階數的數字帶通濾波器，每種階數內有10組不同的濾波器系數，分別對應不同的帶通特性，此為數據集2.采用Voronenko等[18]提供的優化算法庫對數據集2內的濾波器進行優化. Voronenko[18]算法庫為卡內基梅隆大學SPIRAL算法庫的一部分，濾波器優化部分由HCUB算法的提出者Voronenko[18]提供，是一個集成多個主流遞歸式濾波器優化算法的經典算法實現庫，已經被Vinod等[16-17]多位學者引用，可以實現包括BHM、RAG-n、HCUB在內的3種遞歸式濾波器優化算法，量化位寬支持到12 bit，濾波器階數支持到100階左右.由于Parks-McClellan設計法和算法庫的限制，只產生了70組30-100階的濾波器，量化位寬均為12 bit.

3.2 本算法與一維非遞歸算法及傳統CSD表示法的對比

對數據集1內的18組濾波器進行了優化，統計采用CSD表示法、NRSCSE算法和ONRSCSE算法時運算需要的加法器資源，得到結果見表1、2.

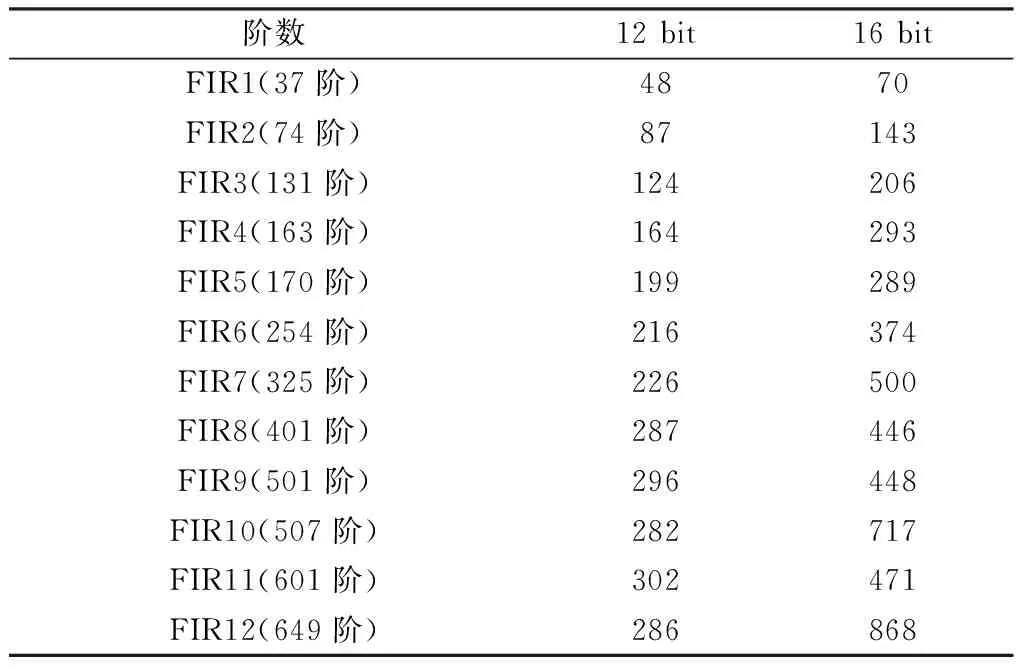
表1 CSD表示法的加法器資源

表2 NRSCSE與ONRSCSE算法優化后的加法器資源

可以看到，與CSD表示法相比，NRSCSE與ONRSCSE優化效果都很顯著.在階數低于100時，優化后的加法器資源均控制在傳統CSD表示法的30%左右；階數高于100時，優化后的加法器資源控制在傳統CSD表示法的50%以內.

比較NRSCSE與ONRSCSE的優化效果發現，同等情況下，ONRSCSE均優于NRSCSE，優化效率見表3.可以看到，ONRSCSE對NRSCSE的優化效率不隨著濾波器階數和量化位寬線性變化，而是主要取決于濾波器經過一維非遞歸優化后的加法器資源.普遍來說,同樣量化位寬的條件下,ONRSCSE對NRSCSE的優化效果呈現一定的比例關系，NRSCSE優化后的加法器個數越多，ONRSCSE節省的加法器個數就相對更大.然而由于經過NRSCSE優化后的殘余系數矩陣的非零位在不同濾波器系數矩陣中分布各異，所以優化效果會體現出個體差異，如FIR10與FIR11，12 bit量化時經過NRSCSE優化后加法器個數分別為109/122個，但是ONRSCSE的節省加法器個數卻是12/9個，FIR11的ONRSCSE優化效果略差于FIR10.這是因為FIR11經過行系數公共項提取后，殘余稀疏矩陣非零位分布相對發散，可以提取的列公共項個數少于FIR10.

表3 ONRSCSE對NRSCSE的提升效果

對上述優化結果的加法器資源進行繪圖，得到ONRSCSE與NRSCSE加法器個數對比,如圖3所示.

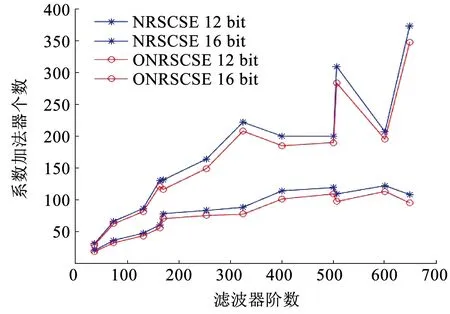
圖3 ONRSCSE與NRSCSE加法器個數對比

與傳統一維非遞歸算法NRSCSE算法相比，采用ONRSCSE算法的優化效果更高，降低加法器資源的比率平均為10.05%(12 bit量化)和7.21%(16 bit量化).同時，優化的效果受階數的變化影響較小，呈現非常穩定的特性.由于ONRSCSE對相鄰系數的共同項提取結果直接通過D觸發器進入下一級運算，對濾波器的邏輯深度沒有影響，因此ONRSCSE和一維非遞歸算法一樣，仍然具有最低邏輯深度特性.

3.3 本算法與傳統算法的比較

對數據集2的7種12 bit量化的濾波器進行優化，分別采用BHM、RAG-n、HCUB、NRSCSE、ONRSCSE算法進行設計，每種濾波器的10組系數優化結果LA與LD進行平均，得到相同階數內濾波器優化的平均優化結果.記錄最終得到的平均加法器個數(Mean logic adder,MLA)和平均邏輯深度(Mean logic depth,MLD)，進行優化效果對比.其中BHM、RAG-n、HCUB的濾波器優化算法由Voronenko[18]提供，優化結果對比見表4.

表4 ONRSCSE與NRSCSE、BHM、RAG-n、HCUB的優化效果對比

對優化結果的加法器資源和邏輯深度進行繪圖，得到算法性能對比如圖4所示。可以看到，在31～101階的一共70組12 bit系數量化濾波器中，非遞歸的濾波器優化算法NRSCSE算法相比于遞歸式算法HCUB、BHM、RAG-n，邏輯深度最低，加法器資源最高，優化后的ONRSCSE算法邏輯深度與NRSCSE算法相同，均保持為最低，但是加法器資源已經明顯優于HCUB、BHM、RAG-n，取得了最好的效果.由于ONRSCSE只依靠系數內的公共項，不利用系數值進行下一步的系數優化，系數間不存在依賴關系，不會對后續的綜合產生影響，非常有利于算法的綜合與實現.

圖4 ONRSCSE/NRSCSE/HCUB/BHM/RAG-n算法的加法器資源與邏輯深度對比

4 結 論

1)本文首次提出了結合系數行公共項優化和列公共項優化的系數矩陣二維優化方法，并將其運用到了非遞歸的FIR濾波器優化算法中，取得了較好的效果. 首先將系數用CSD法表示，降低了系數中的非0值個數；然后對系數矩陣進行行系數分解，降低行系數中的加法器個數；之后對殘余矩陣進行公共項提取，進一步降低整體加法器個數.

2)相比于現有的一維非遞歸算法，本算法可節省10.05%(12 bit量化)和7.21%(16 bit量化)加法器個數.在低階濾波器的優化中，加法器使用量降低到了傳統的CSD表示法的30%左右.仿真結果表明，在階數低于100、量化位寬為12 bit時平均加法器個數和深度指標均優于已發表的NRSCSE、BHM、RAG-n、HCUB算法.