例談小學數學教學中促進深度學習的策略

胡文蘭

摘要：深度學習具有積極參與、充分體驗、意義建構、遷移應用等特征。在小學數學教學中，可以采取以下策略促進學生的深度學習：利用問題驅動，促進積極參與;設計豐富活動，促進充分體驗;抓住知識聯系，促進意義建構;設計變式練習，促進遷移應用。

關鍵詞：深度學習;小學數學;問題驅動;知識聯系;變式練習

北京師范大學郭華教授指出，深度學習“是指在教師引領下，學生圍繞具有挑戰性的學習主題，全身心積極參與、體驗成功、獲得發展的有意義的學習過程”。西北師范大學安富海教授認為：“深度學習是一種基于理解的學習，是指學習者以高階思維的發展和實際問題的解決為目標，以整合的知識為內容，積極主動地、批判性地學習新的知識和思想，并將它們融入原有的認知結構中，且能將已有的知識遷移到新的情境中的一種學習。”綜合看來，深度學習具有積極參與、充分體驗、意義建構、遷移應用等特征。因此，筆者在小學數學教學中，主要采取以下策略促進學生的深度學習。

一、利用問題驅動，促進積極參與

深度學習是積極參與、主動探究的學習。“學起于思，思源于疑。”教師可以利用問題驅動，促進學生積極參與、主動探究。特級教師黃愛華說過：“大問題的一個核心追求是讓學生不教而自會學，不提而自會問。”所以，教師可以設計一些指向核心知識（教學重、難點）的“大問題”，引領整節課的教學，促使學生不僅分析和解決問題，而且發現和提出問題，從而構建“問學現場”，即圍繞各種問題展開深度學習。

例如，《圓的認識》一課伊始，筆者提出如下問題：（1）有4個人參加投球入簍游戲，如圖1、圖2所示的兩種站位設計（圖中正方形中心為球簍所在，字母標示處為投球者站位）公平嗎？為什么？（2）如果是8個人參加投球入簍游戲，如圖3所示的站位設計（圖中正方形中心為球簍所在，字母標示處為投球者站位）公平嗎？為什么？（3）學習了今天的內容后，你能不能為他們找到公平的站位設計方案呢？

這組問題層層遞進，最終指向這節課的核心知識，即圓的特征：同一個圓的半徑都相等。課堂伊始提出這個問題，促使學生全程積極參與、主動探究。認識了圓的特征后，學生就迫不及待地提出：可以將球簍放在圓心位置上，投球的人站在圓上任意一點位置上投球，這樣根據圓的半徑處處相等的特點，可以確定每個人投球的距離一樣，游戲具有公平性。

筆者順勢問道：你還能提出哪些和圓的這個特征相關的問題來考一考大家？學生稍作思考后，七嘴八舌地拋出了自己的問題：為什么車輪要設計成圓形，而不設計成正方形、三角形等其他形狀？怎樣在操場上畫一個直徑是10米的圓？……這樣的“問學現場”促使學生主動探究，深化了學生的思維，提升了學生對圓的特征的認識。

二、設計豐富活動，促進充分體驗

深度學習是充分體驗、激發感悟的學習。“我聽到了，我忘記了;我看到了，我記住了;我做過了，我理解了。”活動，是認識發展的直接源泉和根本途徑。因此，教師應該設計多感官參與的活動，讓學生親身經歷，促進學生充分體驗、激發感悟。

例如，教學《時、分、秒》一課時，讓學生在一分鐘內完成跳繩、做口算題、朗讀課文、寫字等活動，體驗1分鐘有多長;教學《千克與克》一課時，讓學生掂一掂重約1克的回形針，掂一掂重約50克的雞蛋，提一提重約1千克的一袋面粉，搬一搬重約5千克的一袋大米，體驗千克與克分別適用于什么物體的重量計量;教學《米和厘米》一課時，讓學生用米尺分別標記1米高在自己身體上的位置、在教師身體上的位置，體驗1米的不變性與人體的多樣性;教學《面積單位》一課時，讓學生緊挨著站在一起感受1平方米有多大，讓學生手拉手圍成一圈感受100平方米的大小……這樣的活動體驗不僅能促進學生對較小計量單位的感知理解，而且能為學生想象理解較大計量單位奠定基礎。

再如，教學“正、反比例”內容后，筆者組織學生分組完成設計樹木“身份證”的活動：首先引導學生猜想、驗證“同一時間、同一地點，物體的影長與實際高度的比值一定”，然后引導學生據此測量、計算樹木的實際高度，作為樹木“身份證”中的一項重要信息。這樣手腦并用的活動體驗激活了學生的高階思維，促進了學生的深度學習。

三、抓住知識聯系，促進意義建構

深度學習是意義建構的學習，應從個人的原有認知結構出發，加工新的知識，并將其融入原有認知結構。因此，教師要抓住知識之間的聯系，促進學生利用舊知獲得新知（溫故知新），完成意義建構。此外，還要啟發學生抓住知識之間的聯系，靈活轉換知識，獲得解題思路。

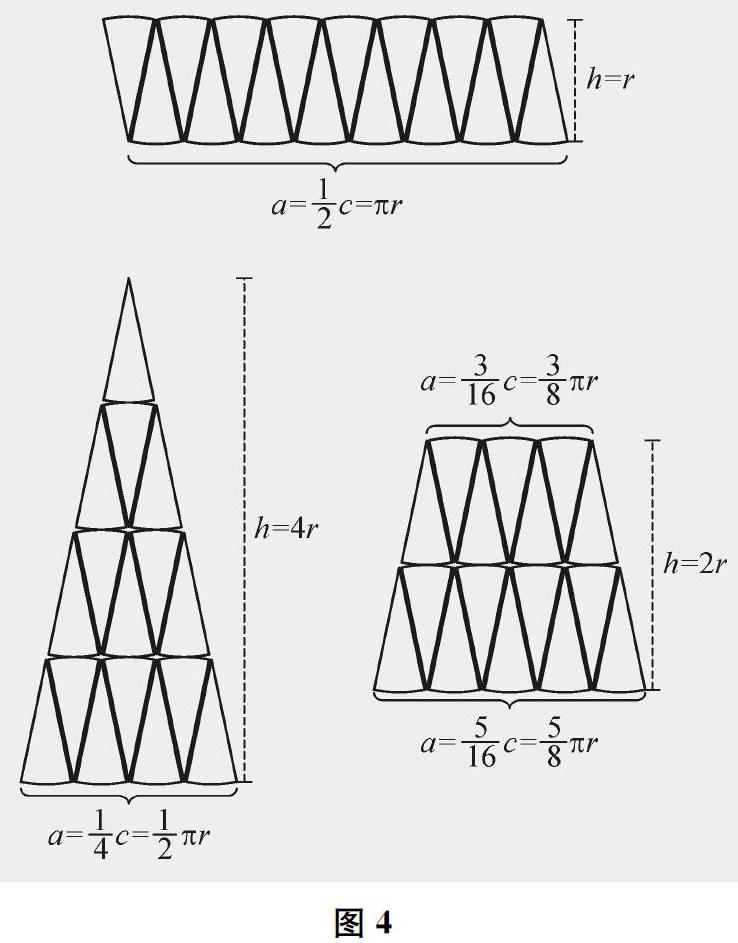
例如，教學《圓的面積》一課時，筆者引導學生開放思考：除了像教材給出的那樣將圓轉化為長方形，還可以將其轉化為什么圖形，從而推導出其面積計算公式？學生積極思考與嘗試，進而在分享與交流中，理順了圓與平行四邊形、三角形、梯形的轉化關系（參見圖4），還將其與轉化為長方形的方法做比較，從而完善了知識結構，培養了發散思維，實現了深度學習。

再如，解決有關分數的實際問題一直是學生學習的難點，很多學生常常無法正確判斷單位“1”，導致在計算的選擇與量率的對應上出錯。為了突破這個難點，教學《比的認識》一課后，筆者精選學生易錯的有關分數的實際問題，編制題組練習，引導學生根據分數與比的關系，將分數關系轉化為比的關系，通過尋找不變量搭橋，找準對應份數來解決。例如，一組練習為：“學校開展興趣小組活動。第一周，美術組的人數是音樂組的23。（1）第二周，又有12人參加了音樂組，這時美術組的人數是音樂組的12，則原來美術組和音樂組各有多少人？（2）第二周，美術組的4人調到了音樂組，這時美術組的人數是音樂組的12，則原來美術組和音樂組各有多少人？”在筆者的引導下，學生得到如圖5所示的解法。這里，學生不僅理順了分數與比的關系，而且通過分數與比的轉化，找到了解決此類問題的有效方法。

四、設計變式練習，促進遷移應用

深度學習是遷移應用的學習，應將已有知識遷移到新的情境中，用來解決新的問題。一般來說，新的情境問題相對于生成已有知識的情境問題都會發生變化。因此，遷移應用可能是積極有效的（正遷移），也可能是消極無效的（負遷移）。對此，教師要設計多樣的變式練習（包括近遷移題、中遷移題、遠遷移題），提升學生掌握相關知識的概括化程度和遷移應用的靈活性，幫助學生打破思維定式，實現正遷移。

例如，教學“正、反比例”內容后，筆者創編如下題目：“電視機屏幕的規格是指對角線的長度，一般用英寸來表示（1英寸≈2.54厘米），屏幕的長寬比為16∶9，如50英寸是指電視屏幕的對角線長50英寸，其長約為112厘米，寬約為63厘米。那么，65英寸電視機屏幕的長約是（）厘米，寬約是（）厘米。”面對繁多的題目信息，學生先是一籌莫展，然后想到剛學習的正比例知識，試圖利用屏幕的長寬比為16∶9來解決，但是，發現要求長和寬兩個量，僅用這個條件是不夠的。于是，有學生關注到對角線長65英寸，試圖將其化為厘米后運用超前學習的初中知識——勾股定理來解決。筆者提示學生畫圖，學生終于想到更早學習的圖形放大、縮小和比例知識，從而利用兩種電視機屏幕的長、寬、對角線成比例來解決。

再如，教學《比較分數的大小》一課時，學生掌握同分母分數比較大小和通分后，面對異分母分數比較大小的題目，總是想到轉化成同分母分數再比較。對此，筆者設計變式題組，引導學生學會根據不同的分數特征，選擇不同的比較方法：（1）一個真分數和一個假分數，直接比;（2）和1相差相同個分數單位的兩個分數，和中間量 1比;（3）一個大于12，一個小于12，和中間量12比;（4）分母較大的兩個分數，分子通分后再比較;（5）兩個假分數，轉化成帶分數后，先比較整數部分，再比較真分數部分;（6）多個分數、小數排序，轉化成小數再比較。

參考文獻：

[1] 沈重予，王林.小學數學內容分析與教學指導[M].南京：江蘇鳳凰教育出版社，2015.

[2] 郭華.深度學習及其意義[J].課程·教材·教法，2016（11）.

[3] 安富海.促進深度學習的課堂教學策略研究[J].課程·教材·教法，2014（11）.

[4] 張姝華，喻平.問題解決中遷移的心理學研究及其對中學數學教學的啟示[J].教育研究與評論（中學教育教學），2019（9）.