橋梁渦振幅值響應質量阻尼敏感性影響研究
周 帥 鄒云峰 方 聰 牛華偉
(1.中國建筑股份有限公司,北京 100013;2.湖南大學,長沙 410082;3.中南大學,長沙 410075)
隨著現代橋梁抗風理論的進一步完善,顫振、馳振等一類發散性的風致振動在大跨度橋梁中得到了有效的防治。但渦激共振作為一類限幅流固耦合振動,在大長細比鈍體橋梁構件中易發、頻發,影響橋梁結構的正常使用,引發構件疲勞振動風險[1-2]。如何提高幅值的估算水平,準確預測工程結構的渦振幅值響應,提前制定好控制措施,將渦振幅值響應控制在可接受的量值范圍內,成為了工程應用研究的方向之一[3-4]。
目前,國內、外專家學者作了大量的研究,Euro Code[5-6]針對鈍體橋梁構件的渦振幅值估算做了系統的研究工作,提出了基于質量阻尼參數(Scruton數)為基礎的幅值估算經驗公式[7-8]。文獻[9]認為渦激共振幅值是結構斷面幾何參數、質量阻尼參數的函數,渦振幅值與質量阻尼呈反比例關系。文獻[10]的研究表明,質量、阻尼是影響渦振幅值的唯一參數,同時基于大量實測數據開展多項式擬合得出了基于質量阻尼參數和Reynolds數的渦振幅值估算經驗公式。Tamura、Scanlan[11-12]等基于不同的渦激力模型同樣得到了幅值估算公式,其中,渦振幅值與質量阻尼參數并非呈現明確的線性關系。文獻[13-14]研究表明質量、阻尼對于渦激共振幅值的影響是不獨立的,兩者不能組合成Scruton數對渦振幅值進行評估。
綜上所述,關于質量、阻尼參數對渦激共振幅值的影響獨立性及權重敏感性有待進一步研究。本文基于一組矩形截面節段模型,通過調整模型系統質量、阻尼、剛度,在Reynolds一致的情況下,單參數變化等效質量和阻尼,開展測振風洞試驗,實測渦激共振幅值響應,研究相關問題。
1 渦振幅值估算理論模型
單自由度渦激力模型渦激氣動力可表述為:
(1)
式中:P(t)——渦激氣動力;
ω——振動圓頻率;
ψ——結構位移響應與渦激力的相位差;
t——時間;
ρ——空氣密度;
D——截面橫風向尺寸;
U——來流速度;
CL——升力系數均方根。
渦激共振狀態下,結構振動卓越頻率與尾流渦脫頻率一致,相位相同,結構渦激共振位移響應可表述為:
Y(t)=Ymax×sin(ωt+ψ)
(2)
式中:Y(t)——渦激振動位移響應;
Ymax——位移響應幅值。
由結構動力學方程可得渦激在氣動力作用下結構位移幅值為:
(3)
式中:h——渦激力展向相關長度;
φn(x)——結構第n階振型;
Mn——結構第n階等效質量;
ωn——結構第n階固有圓頻率;
ξn——結構第n階固有阻尼比。
結構第n階振型無量綱渦振位移幅值為:
(4)
式中:K——結構第n階模態振型修正系數;
St——結構橫截面Strouhal數,St=fnD/U;
m*——勻質結構每延米物理質量;
Sc——結構Scruton數,Sc=4πm*ξn/(ρD2);
fn——結構第n階模態固有工程頻率;
Kw——相應的渦激力展向相關性系數。
式(4)為Euro Code渦振幅值估算經驗公式的理論基礎[15],從式中可以看出,渦激共振幅值與Scruton數呈反比例關系,等效質量、阻尼比對渦振幅值的影響權重相同。
2 試驗模型及參數
2.1 風洞試驗模型
彈性懸掛剛性節段模型如圖1所示。8根豎向安裝彈簧懸掛二維剛性節段模型,提供節段模型系統豎向剛度和扭轉剛度。模型系統存在豎向(Heaving)、扭轉(Pitching)、搖擺(Rolling)三種不同的振動形態,通過調節懸掛彈簧的橫向間距,提高扭轉剛度,可以使模型振動為純豎向(Heaving)振型。通過配重增減可以實現節段模型系統等效質量的調節,阻尼比的調節通過在彈簧纏繞膠帶的方式實現。
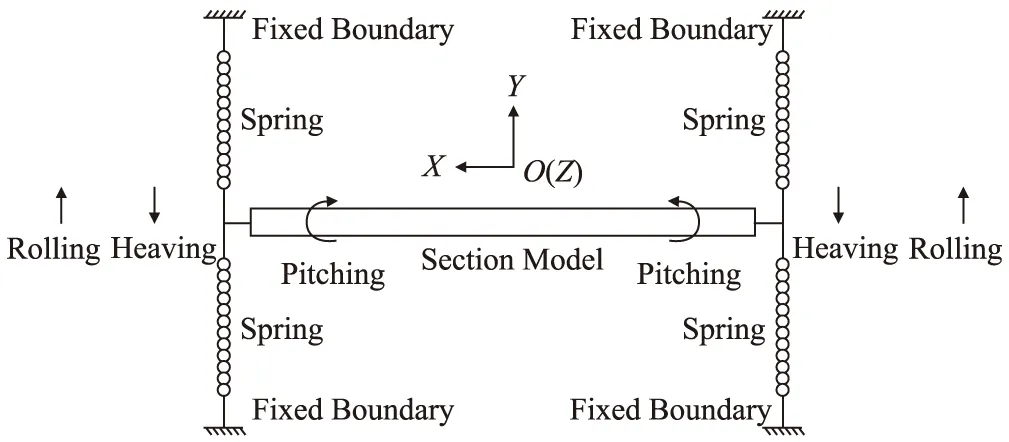
圖1 風洞試驗節段模型系統圖
矩形截面節段模型尺寸為100 mm×120 mm×1 530 mm。調整模型截面至短邊迎風、長邊迎風狀態,可實現截面寬高比B/D=1.2、0.83兩組不同的試驗工況。測振試驗采用加速度傳感器,4個傳感器布置在節段模型水平連桿上,分布在前后左右4個不同的位置,如圖2所示。基于4個通道加速度響應的相位信息判別模型振動豎向(Heaving)、扭轉(Pitching)、搖擺(Rolling)振型,取均值可得到豎向振動響應,取差值可分別得到扭轉、搖擺振動響應。試驗過程中,渦激共振鎖定區間內,4個加速度傳感器時程曲線相位一致,模型振動為豎向振型,振動頻率卓越(與豎向固有頻率一致),為標準的單頻簡諧振動,可以方便地由加速度響應計算得到位移響應。
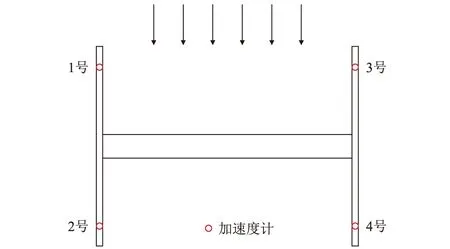
圖2 測振傳感器安裝圖
2.2 主要工況及參數
通過調整節段模型系統等效質量、阻尼和剛度參數,可得到工況及參數列表如表1所示。等效質量分別為12.66 kg/m、17.95 kg/m、24.60 kg/m三組不同的量級,同步更換懸掛彈簧,對應調整等效剛度,使得不同質量參數下模型系統豎向(Heaving)固有頻率一致,均為2.93 Hz。豎向阻尼比分為0.146%、0.200%、0.284%、0.500%共4組不同的水平。優化組合節段模型系統截面寬高比(B/D)、質量、阻尼、彈簧剛度參數,實現C1~C16共計16組不同的試驗工況,Scruton數范圍12.4~82.5,可以實現對單一變化質量參數、單一變化阻尼參數、以及Scruton數相同(24.1)不同質量阻尼參數組合工況下渦激共振幅值響應的對比研究。
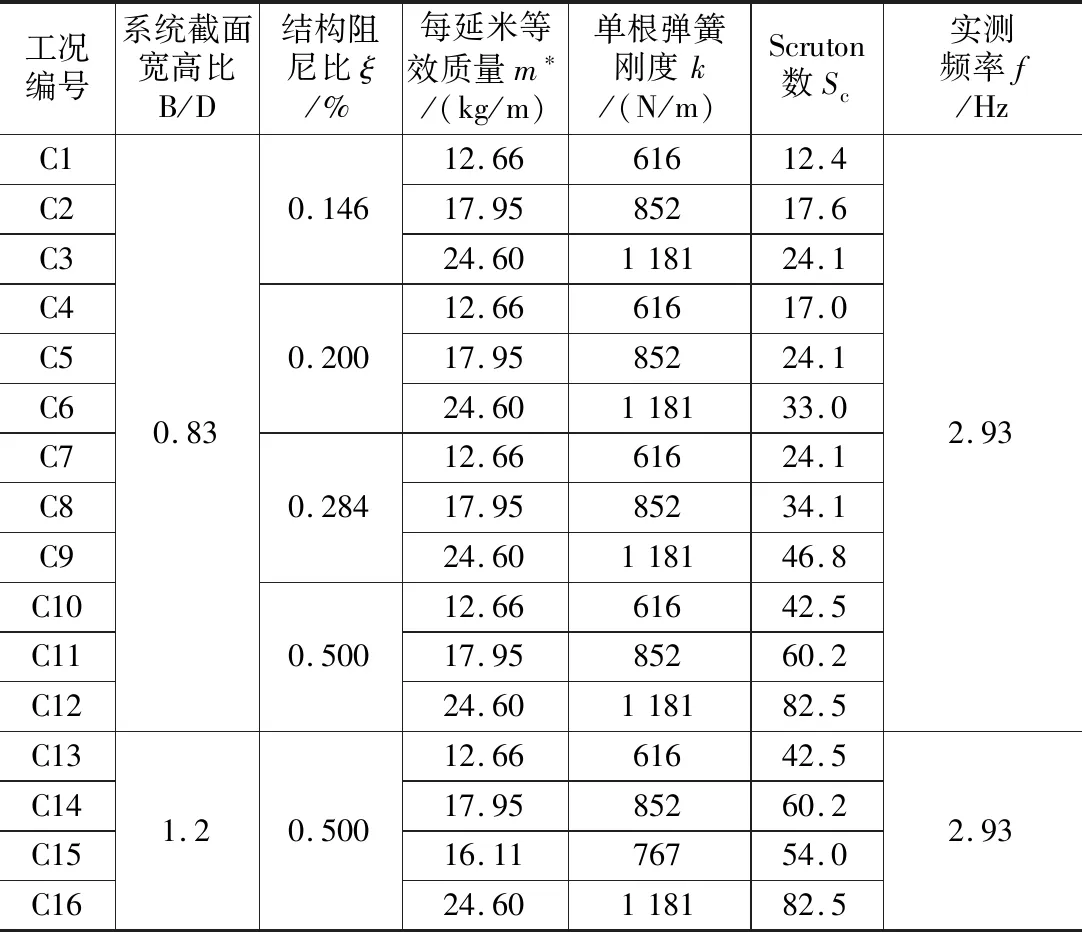
表1 研究工況及參數表
3 結果及分析
測振風洞試驗實測到了表1所示的C1~C16工況不同狀態的風致振動響應,包括渦激共振鎖定區間響應、渦激氣動力與準定常馳振氣動力耦合作用產生的“軟馳振”響應以及發散性的馳振響應等不同狀態響應,限于篇幅,本文將主要列舉產生了渦激共振響應的試驗工況,對比分析質量、阻尼參數對渦振幅值的影響。
3.1 質量參數影響
試驗實測節段模型系統風致振動典型時程曲線及頻譜如圖3、圖4所示,對應C13工況渦激共振鎖定區間幅值響應點,無量綱風速11.9,無量綱位移幅值0.176。加速度響應曲線顯示基本為等幅振動狀態,頻譜分析卓越頻率2.93 Hz,與模型系統豎向固有頻率一致,為單頻振動狀態。
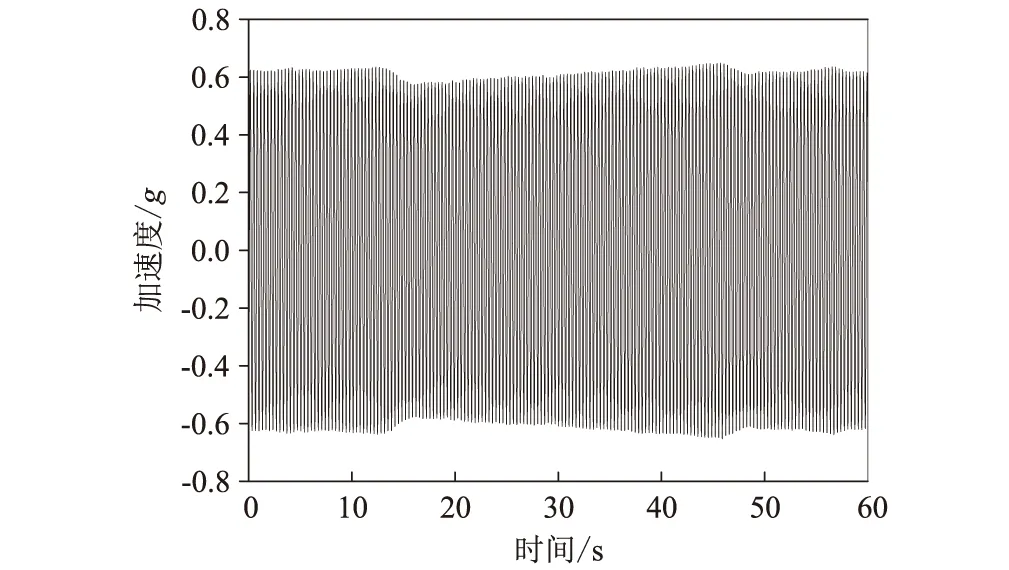
圖3 工況C13渦振幅值點時程圖
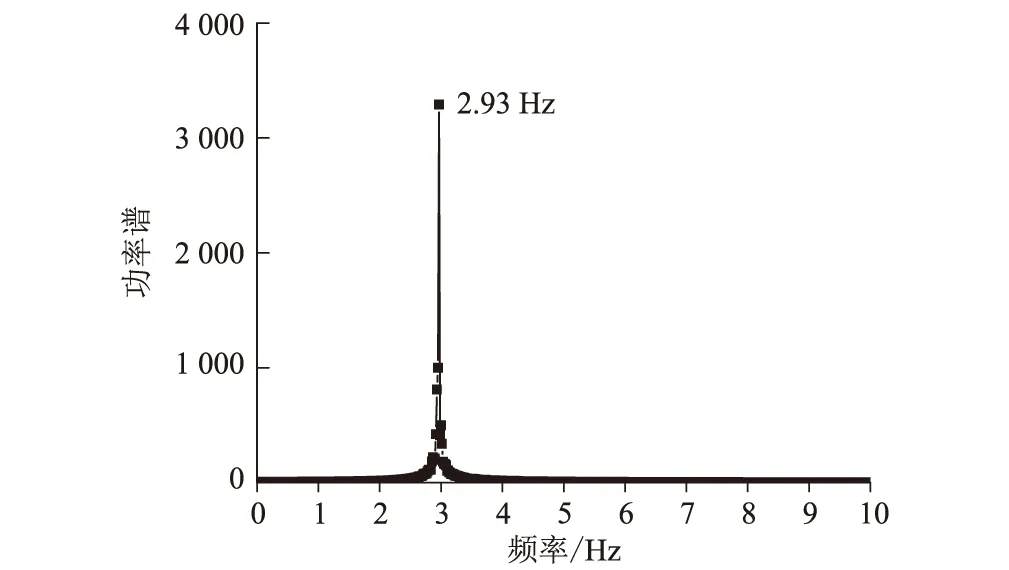
圖4 工況C13渦振幅值點頻譜圖
對應C13~C16工況,相同阻尼比(ξ=0.500%),不同等效質量(m*=12.66 kg/m、16.11 kg/m、17.95 kg/m、24.60 kg/m)組合參數下,無量綱風速-位移響應曲線如圖5(a)所示。隨著風速的增加,風振響應曲線出現了渦激共振鎖定區間和“軟馳振響應”,渦激共振鎖定區間放大如圖5(b)所示。從圖5可以看出,渦激共振幅值隨著質量的增加而減小,等效質量參數量值由12.66 kg/m增大到24.60 kg/m,增大比例關系為1.9,實測渦振幅值由0.176降低到0.016,幅值降低比例達到11.0,渦振幅值的降低幅度遠大于質量增加的幅度。
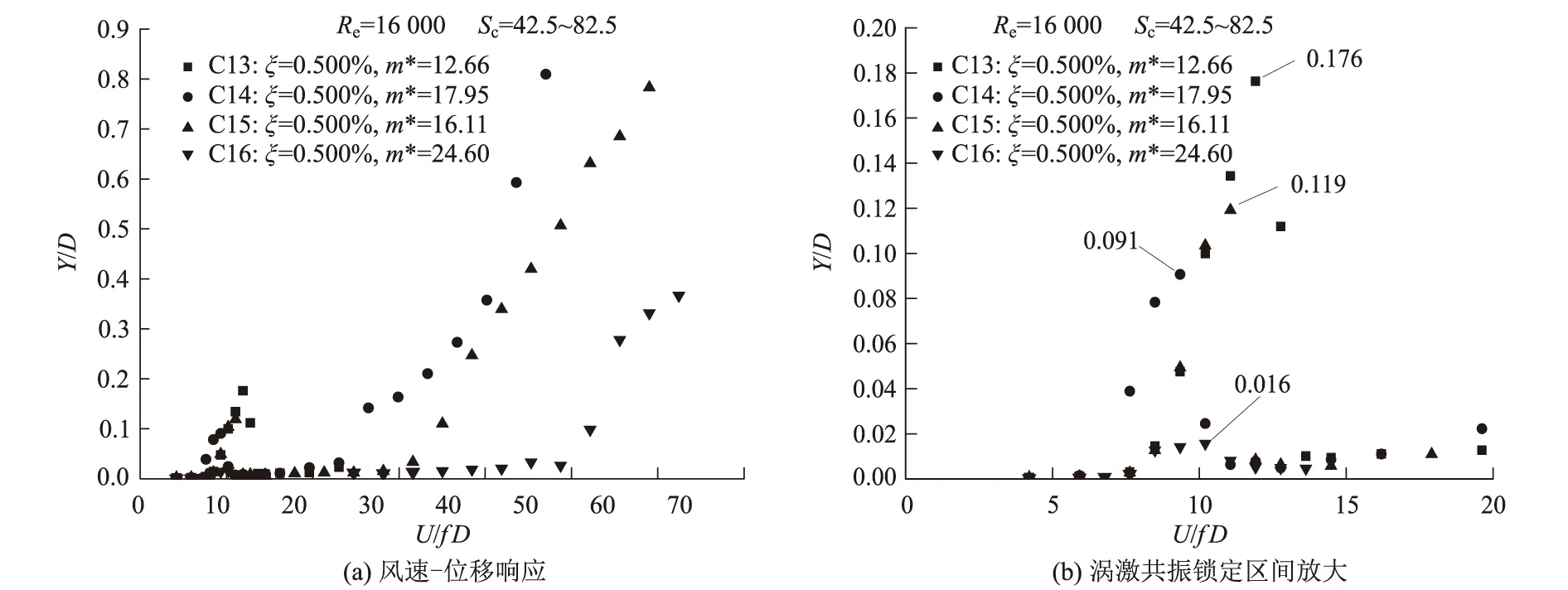
圖5 ξ=0.500%不同質量響應對比圖
3.2 阻尼參數影響
單參數變化阻尼,實測渦激共振響應如圖6~圖8所示。對應C3、C6、C9、C12工況,等效質量m*=24.60 kg/m,阻尼比分別為ξ=0.146%、0.200%、0.284%、0.500%。典型的風致振動時程曲線如圖6、圖7所示,對應C3工況渦激共振鎖定區間最大幅值響應點,無量綱風速、幅值分別為9.9和0.083,從圖7、圖8可以看出,模型振動為單頻振動,振動卓越頻率與豎向固有頻率一致,時程曲線為非等幅狀態,有小幅的“拍現象”,通過對固定時長60 s取方差的方式對幅值響應進行評估。
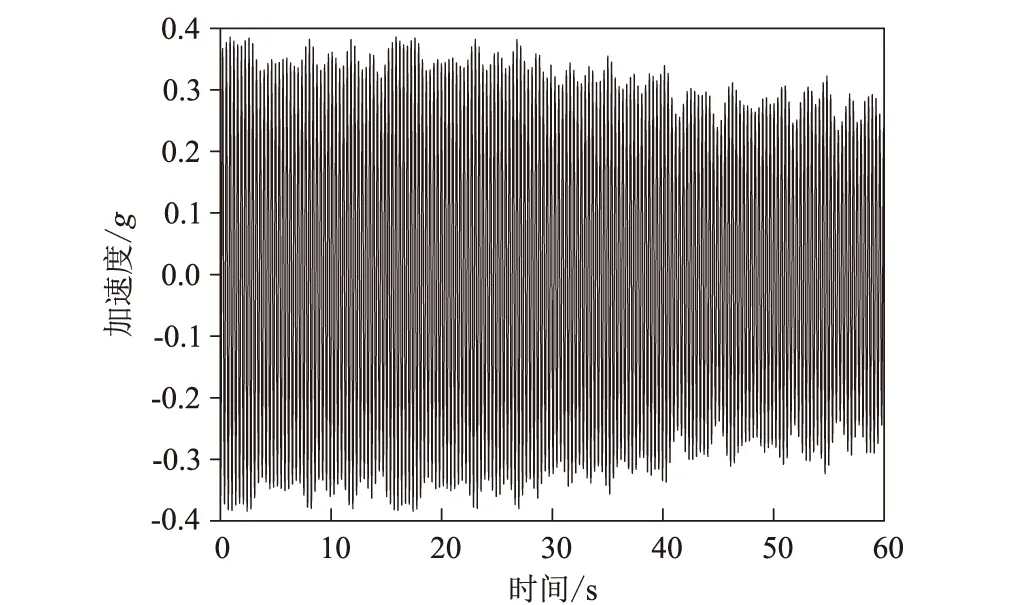
圖6 工況C3渦振幅值點時程圖
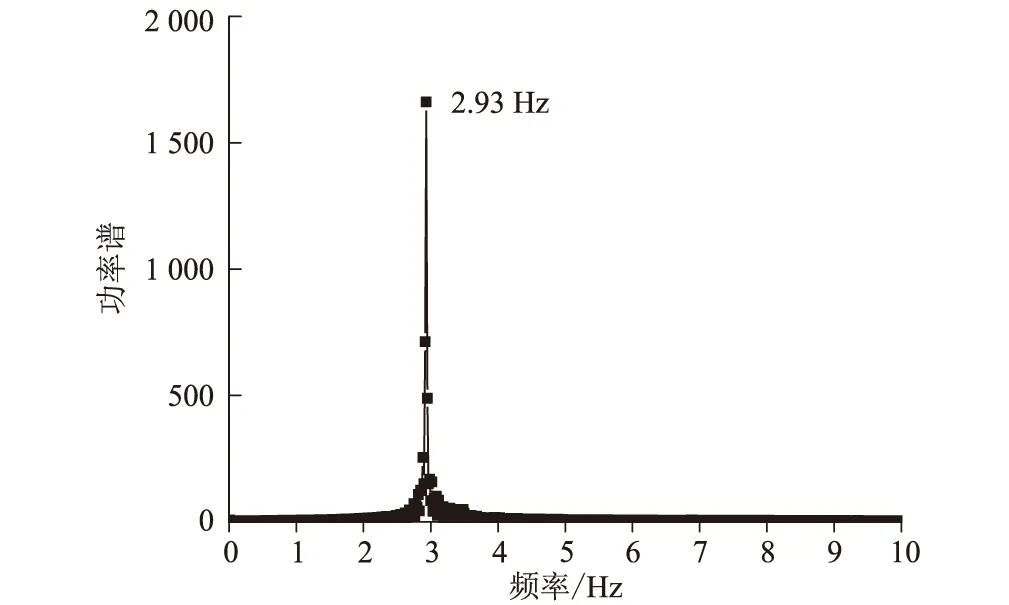
圖7 工況C3渦振幅值點頻譜圖
從圖8可以看出,阻尼比變化范圍較大,由0.146%增大到 0.500%,變化幅度達到3.4倍,對應實測渦激共振鎖定區間內無量綱位移幅值響應從小到大分別為0.029、0.043、0.066、0.083,最大、最小幅值比為2.9,與阻尼增大幅度基本相當。
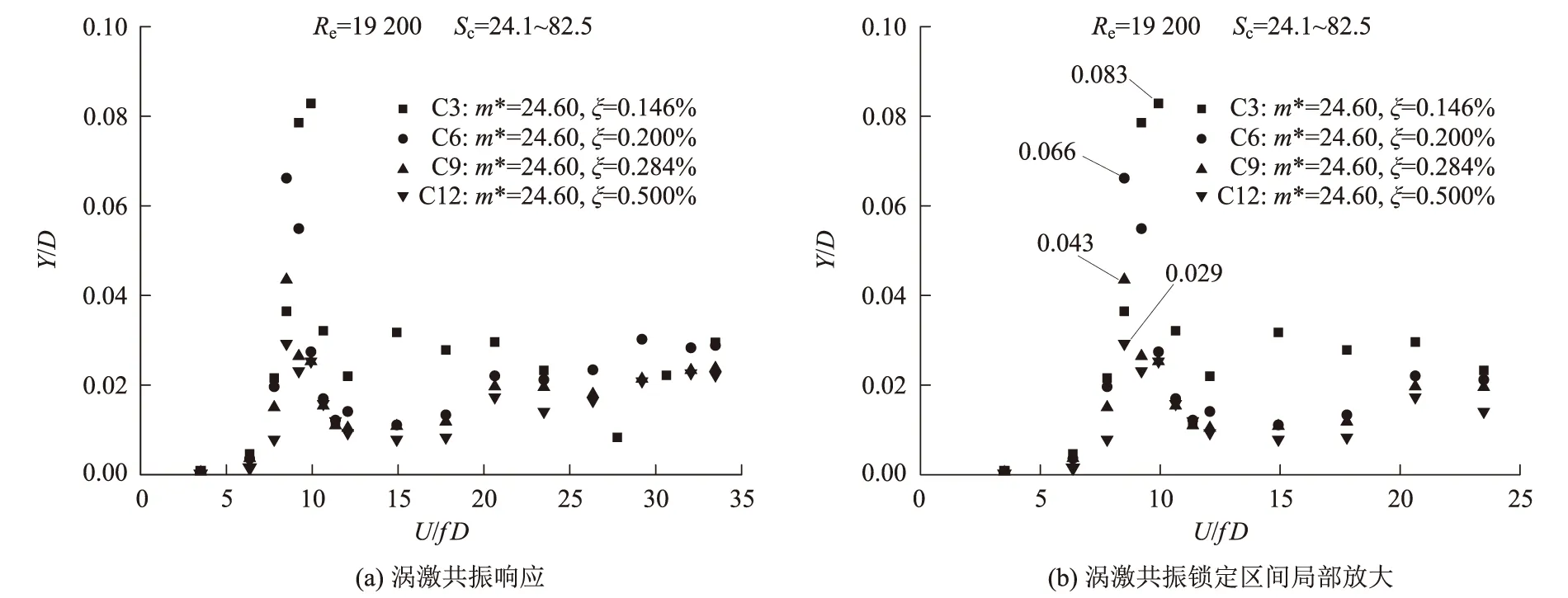
圖8 m*=24.60 kg/m不同阻尼響應對比和渦振響應圖
3.3 敏感性分析
從工況列表中選取相同Scruton數情況下(24.1)不同質量、阻尼參數組合工況風振響應曲線對比如圖9(a)所示,渦激共振鎖定區間局部放大如圖9(b)所示。C3、C5、C7工況,等效質量分別為m*=24.60 kg/m、17.95 kg/m、12.66 kg/m,相應阻尼比分別為ξ=0.146%、0.200%、0.284%,質量阻尼參數組合下Scruton均為24.1,其余結構和流場參數豎向固有頻率、Reynolds數、模型截面迎風高度、風攻角、紊流度等均相同。從圖9中可以看出,無量綱渦激共振位移幅值響應分別為0.031、0.049、0.083,最大、最小幅值比達2.7,并沒有因為Scruton數相同而呈現出渦振幅值相同的狀態。
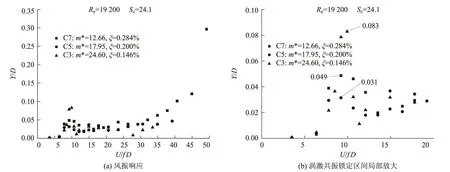
圖9 Sc=24.1不同質量阻尼組合響應和渦振響應圖
各工況對比風洞試驗實測結果顯示,渦激共振幅值響應隨著質量、阻尼的增大而減小。將最小實測渦振幅值和單參數變化質量、阻尼進行歸一化對比,得到敏感性分析如表2所示。表2中,計算值為基于Euro Code渦激共振幅值估算理論,得出位移幅值響應與質量、阻尼呈反比例關系,再根據各工況參數,以最小質量、阻尼為基礎歸一化的比值關系[15]。實測值為以各工況最小實測渦振幅值為基礎歸一化的比值關系。
從表2中可以看出,隨著單參數從小到大變化等效質量(m*)由1.0增大到1.9,實測渦振幅值由1.0降低到1/11.0,幅值降低幅度遠大于質量增加的幅度,并非呈線形反比例關系。單參數增加阻尼比由1.0增至3.4,實測渦振幅值由1.0逐步降低到1/2.9,渦振幅值的降低幅度與阻尼的增加幅度基本相當。現有Euro Code渦激共振理論認為質量、阻尼對于渦激共振幅值的影響權重是一致的,將實測數據對比分析可知,渦激共振幅值的質量敏感性遠大于阻尼敏感性。
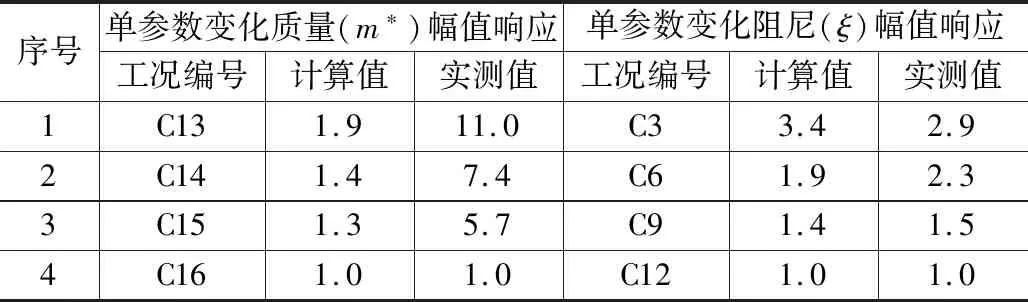
表2 渦振幅值響應質量阻尼參數敏感性分析表
4 結論
本文開展測振風洞試驗,實測渦激共振幅值響應進行對比研究,得出以下主要結論:
(1)實測渦振幅值響應隨著質量、阻尼的增大而減小,定量比例關系分析表明渦振幅值響應的質量敏感性大于阻尼。
(2)相同Scruton(24.1)數不同質量(12.66 kg/m、17.95 kg/m、24.60 kg/m)、阻尼(0.146%、0.200%、0.284%)參數組合工況下,實測渦振幅值響應各不相同,最大最小幅值響應比值達到2.7,驗證了質量、阻尼參數對渦振幅值的影響權重不相同。
(3)單參數變化節段模型系統等效質量,等效質量由1.0增大1.9倍,實測渦振幅值響應由1.0降低到1/11.0,比例關系顯著放大;單參數變化模型系統阻尼,阻尼由1.0增大到3.4,實測渦振幅值由1.0降低到1/2.9,比例關系基本持平。

