鐵路建筑限界曲線加寬通用計算方法研究

趙振剛

(中鐵工程設計咨詢集團有限公司濟南設計院，濟南 250022)

1 現行鐵路建筑限界曲線加寬規定、存在的問題及研究現狀

目前，鐵路行業建筑限界執行《鐵路技術管理規程》和GB 146.2《標準軌距鐵路建筑限界》的規定。計算車型為二軸車，車體長度l=26 m，車輛定距S=18 m，車輛前懸、后懸q= 4 m。規范規定了圓曲線地段內外側限界加寬方法，即在直線-緩和曲線-圓曲線過渡段可采用階梯型方式或曲線圓順方式，雖給出了階梯型加寬的具體方法，但未明確曲線圓順加寬的具體方法。

目前，許多專家學者開展了相關研究，周兵和[1]創造性地繪出了緩和曲線內外側限界加寬值分布示意圖，提出了緩和曲線鐵路建筑限界加寬方法，對加寬曲線中曲線部分采用了直線擬合的方式，車型采用鐵路行業規定的計算車型。趙振剛[2]繪制了緩和曲線段加寬值曲線示意圖，采用多項式擬合的方法對加寬值線的曲線部分進行擬合，分段給出了加寬值計算式。但僅適用于鐵路行業標準計算車型。李長準、李明煒[3-4]利用數學分析方法，創造性地提出了不同車型參數，不同線路平面參數下，直-圓過渡段、直-緩-圓過渡段鐵路建筑限界加寬計算方法，公式簡單，方法明確，較好地解決了方法的通用性問題。但經驗證，在小半徑曲線條件下，在緩和曲線起點處誤差較大。在緩和曲線與圓曲線連接處加寬值線與實際不符，誤差值較大。張徐[5]利用MATLAB軟件，分析了地鐵車輛在圓曲線、緩和曲線及曲線過渡段的限界加寬量，繪制了內外側加寬值曲線。溫雙義[6]通過幾何分析方法，闡述了緩和曲線與圓曲線加寬值的比值成正比例關系，提出限界緩和曲線地段加寬計算的比值加寬法。

作為鐵道行業基礎性標準，對直-圓過渡段、直-緩-圓過渡段建筑限界加寬計算方法進行研究，明確過渡段加寬值變化規律，提出適應不同車型、不同線路平面參數的曲線加寬值計算方法是必要的。筆者利用VB軟件編制了建筑限界曲線加寬值計算程序，可進行不同車輛尺寸、不同線路平面參數曲線內、外側及超高加寬計算，可生成線路平面及車體動態中心線圖解圖形、內外側加寬值曲線圖形，導出各里程點的加寬值。

2 技術路線

2.1 研究目標

提出不同車輛定距、不同車輛懸長、不同曲線半徑、不設緩和曲線或不同緩和曲線長度、不同計算里程共五個變量條件下，建筑限界曲線內外側加寬值計算式。

2.2 技術路線

(1)不設緩和曲線時，結合站場手冊規定的加寬公式，以計算機程序生成的不同計算條件的圖解法大數據為基礎，繪制加寬值曲線圖，利用MATLAB軟件分析總結各加寬值變化規律，提出不設緩和曲線時，曲線內外側通用加寬計算式。

(2)設緩和曲線時，以計算機程序生成的圖解法大數據為基礎，繪制不同計算條件下加寬值曲線圖，利用MATLAB軟件分析曲線特征點(如交點)規律，提出特征點計算式；在特征點計算式基礎上，結合參考文獻中的資料，利用MATLAB軟件，分段分析提出設緩和曲線時，曲線內外側通用加寬計算式。

(3)與計算機程序生成的圖解法數據進行對比，驗證通用計算式的誤差和正確性。

限于篇幅，本文間隔列出部分圖解法基礎數據和分析過程。驗證不列具體過程，僅給出結論。為便于驗證、理解，給出的計算式未化簡。

3 建筑限界曲線加寬計算參數

3.1 計算變量及符號

包括曲線半徑R、緩和曲線長l、車輛定距S、車輛懸長q、計算點里程x共5個變量。車型按二軸車，即不考慮轉向架的曲線橫向偏移量。

3.2 里程及單位約定

本文中以ZY點、ZH點里程為+000，ZY點、ZH點前里程為負值。除加寬值單位以mm計外，其他尺寸單位均以m計。

4 不設緩和曲線時建筑限界曲線加寬

4.1 不設緩和曲線時建筑限界曲線內側加寬

4.1.1 圖解法數據及內側加寬值示意圖

主要影響變量為車輛定距S及半徑R。通過圖解法數據，得出R=600 m、S=12 m；R=600 m、S=14 m；R=600 m、S=16 m；R=600 m、S=18 m；R=600 m、S=24 m；R=300 m、S=16 m不設緩和曲線時各點的內側加寬值，如表1所示。以R=600 m、S=18 m為例繪制不設緩和曲線時內側加寬值示意圖，如圖1所示。

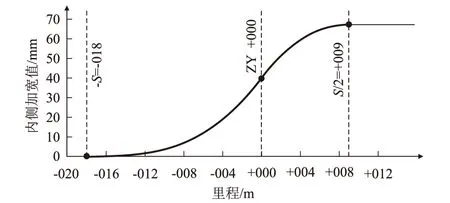
圖1 R=600 m，S=18不設緩和曲線時內側加寬值示意圖

《鐵路工程設計技術手冊 站場及樞紐》規定了不設緩和曲線時直線與圓曲線過渡地段變加寬計算方法：

(1)不設緩和曲線時曲線內側變加寬(m)

以ZY點前18 m為里程0點，曲線ZY點前18 m至ZY點曲線內側變加寬為：

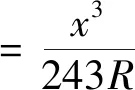
(1)

ZY點至ZY點后9 m曲線內側變加寬為：

(2)

(2)不設緩和曲線時曲線外側變加寬(m)

以ZY點前22 m為里程0點，曲線ZY點前22 m至ZY點前4 m，曲線外側變加寬為：

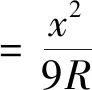
(4)

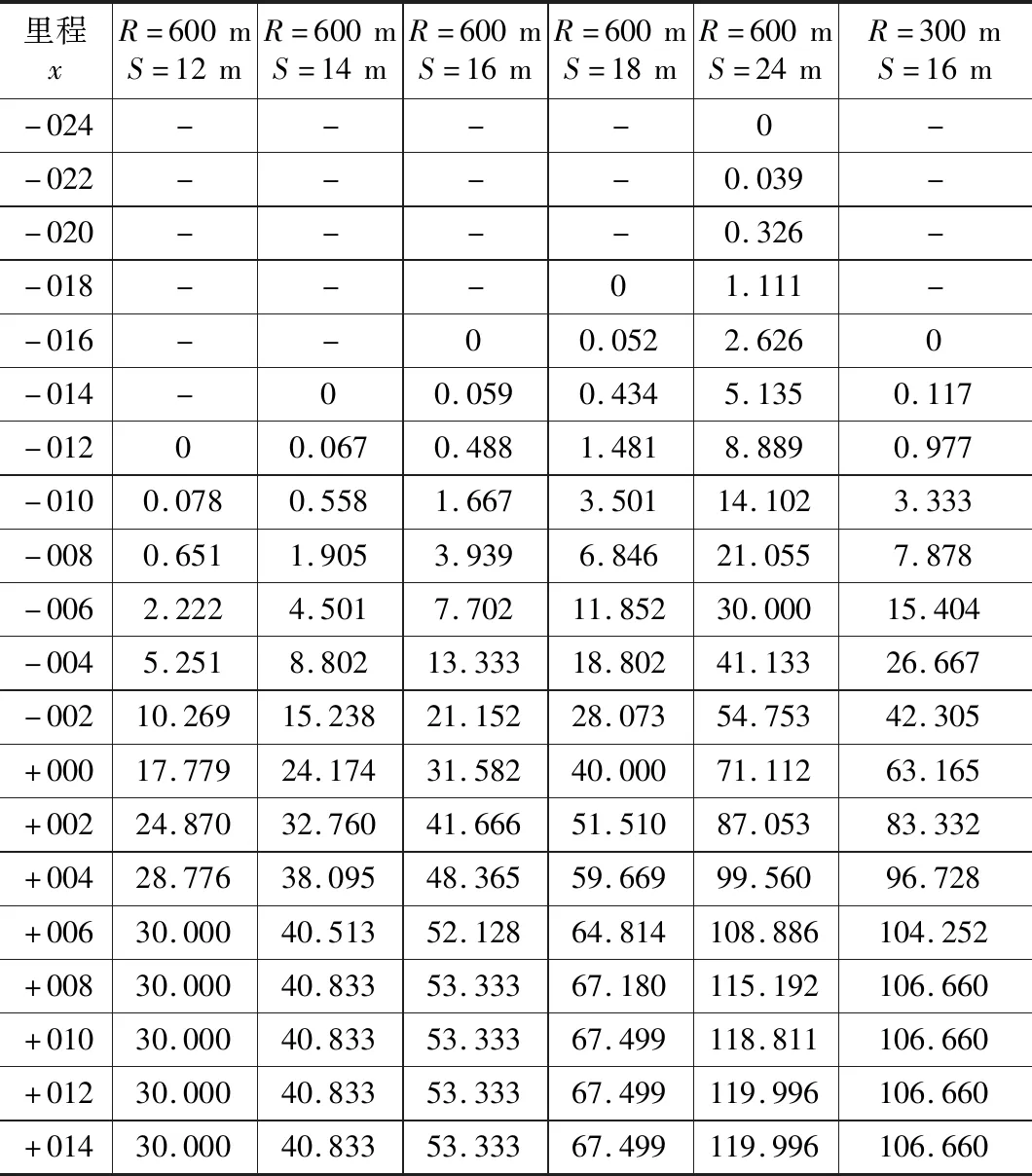
表1 不設緩和曲線時內側加寬值表(mm)

(3)

ZY點前4 m至ZY點，曲線外側變加寬為：

4.1.2 內側加寬值特征點及分段分析

(1)根據圖1和式(1)，特征點定為ZY點前定距點、ZY點和ZY點后1/2倍定距點。

(2)ZY點前定距點至ZY點：利用MATLAB軟件輔助分析，將ZY點(即表1中里程為+000點)加寬值參照式(1)格式進行整理，如表2所示。

表2 不設緩和曲線地段ZY點內側加寬值表

參考式(1)，可得出不設緩和曲線時ZY點前定距點至ZY點曲線內側加寬計算式為：

(5)

經驗證，采用式(5)計算結果與表1中各組合加寬值差值在0.045～-0.002 mm之間。

(3)ZY點至ZY點后1/2倍定距點

利用MATLAB軟件，ZY點后1/2倍定距點處加寬值參照式(2)、式(5)整理，如表3所示。

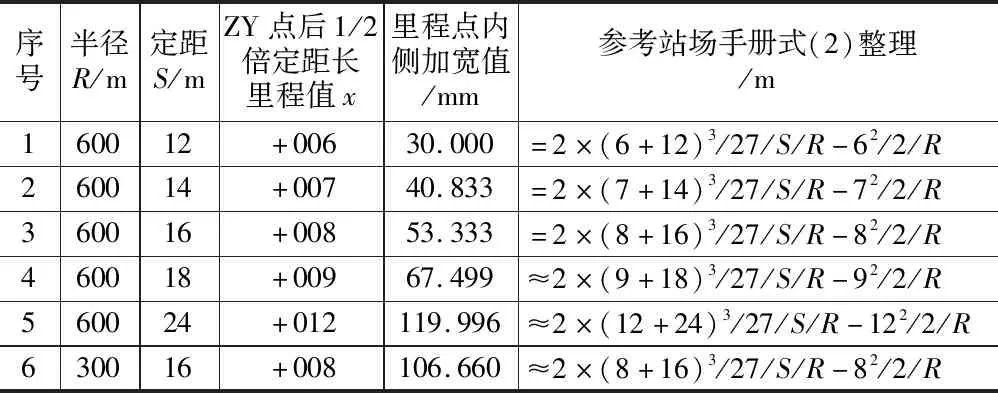
表3 不設緩和曲線地段ZY點后1/2倍定距長處內側加寬值表

參考式(2)、式(5)，可得出不設緩和曲線時ZY點至ZY點后1/2倍定距點曲線內側加寬計算式：

(6)

經驗證，采用式(6)計算結果與表1中各組合加寬值差值在0.069～0 mm之間。

4.2 不設緩和曲線時建筑限界曲線外側加寬

4.2.1 圖解法數據及外側加寬值示意圖

主要影響變量為車輛定距S、懸長q及半徑R，通過圖解法數據，得出R=600 m、S=12 m、q=4 m；R=600 m、S=16 m、q=4 m；R=600 m、S=18 m、q=4 m；R=600 m、S=16 m、q=5 m；R=300 m、S=16 m、q=5 m、R=300 m、S=18 m、q=6 m不設緩和曲線時各點的內側加寬值，如表4所示。以R=600 m、S=18 m、q=4 m為例繪制不設緩和曲線時外側加寬值示意圖，如圖2所示。

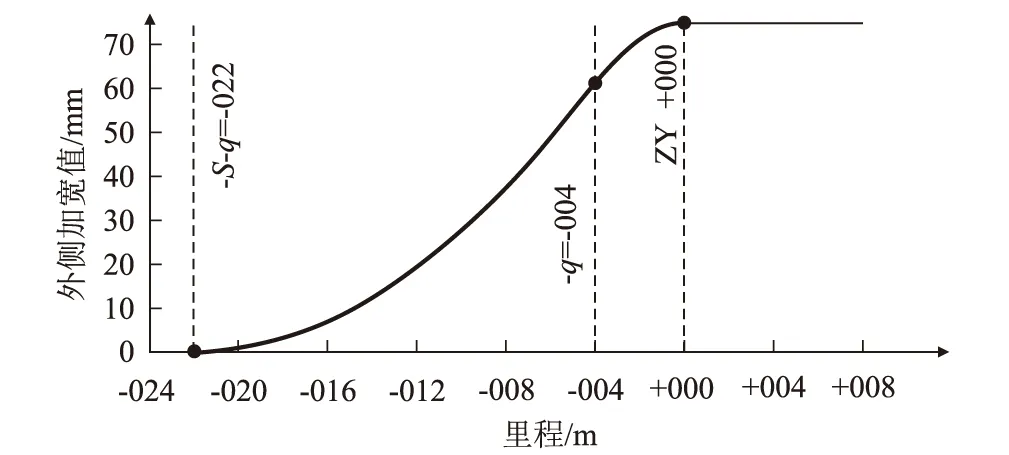
圖2 R=600m，S=18，q=4 m不設緩和曲線時外側加寬值示意圖

4.2.2 外側加寬值特征點及分段分析

(1)結合圖2和式(3)，特征點定為ZY點前定距加懸長點、ZY點懸長點和ZY點。

(2)ZY點前定距加懸長點值ZY點前懸長點：利用MATLAB軟件，將ZY點前懸長點加寬值參照式(3)進行整理，如表5所示。

參考式(3)分析整理后，可得出不設緩和曲線時ZY點前定距加懸長點至ZY點前懸長點曲線外側加寬計算式：

(7)

經驗證，采用式(7)計算結果與表4中各組合加寬值差值在0.007～-0.000 4 mm之間。

(3)ZY點前懸長點至ZY點：利用MATLAB軟件，對ZY點前懸長點至ZY點外側加寬值參考式(4)、式(7)整理，如表6所示。

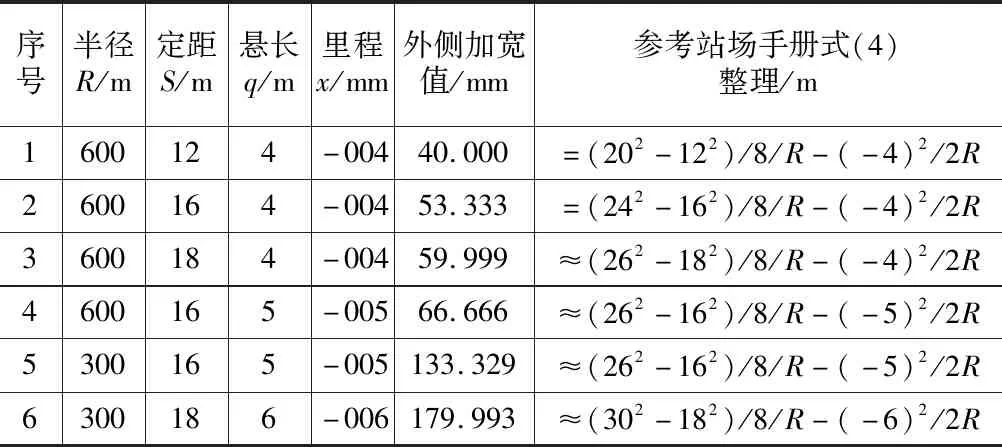
表6 不設緩和曲線ZY點前懸長點外側加寬值表

參考式(4)、式(7)分析整理后，可得出不設緩和曲線時ZY點前懸長點至ZY點曲線外側加寬計算式：

(8)

經驗證，采用式(8)計算結果與表4中各組合加寬值差值在0.018～0 mm之間。

5 設緩和曲線時建筑限界曲線內外側加寬

5.1 設緩和曲線時建筑限界曲線內側加寬

5.1.1 圖解法數據及內側加寬值示意圖

影響變量為半徑R、緩和曲線長l及車輛定距S。通過圖解法數據，得出不同車輛尺寸、不同線路平面參數設緩和曲線時內側加寬值如表7所示。以R=600 m、l=100 m、S=20 m為例繪制設緩和曲線時內側加寬值示意圖，如圖3所示。

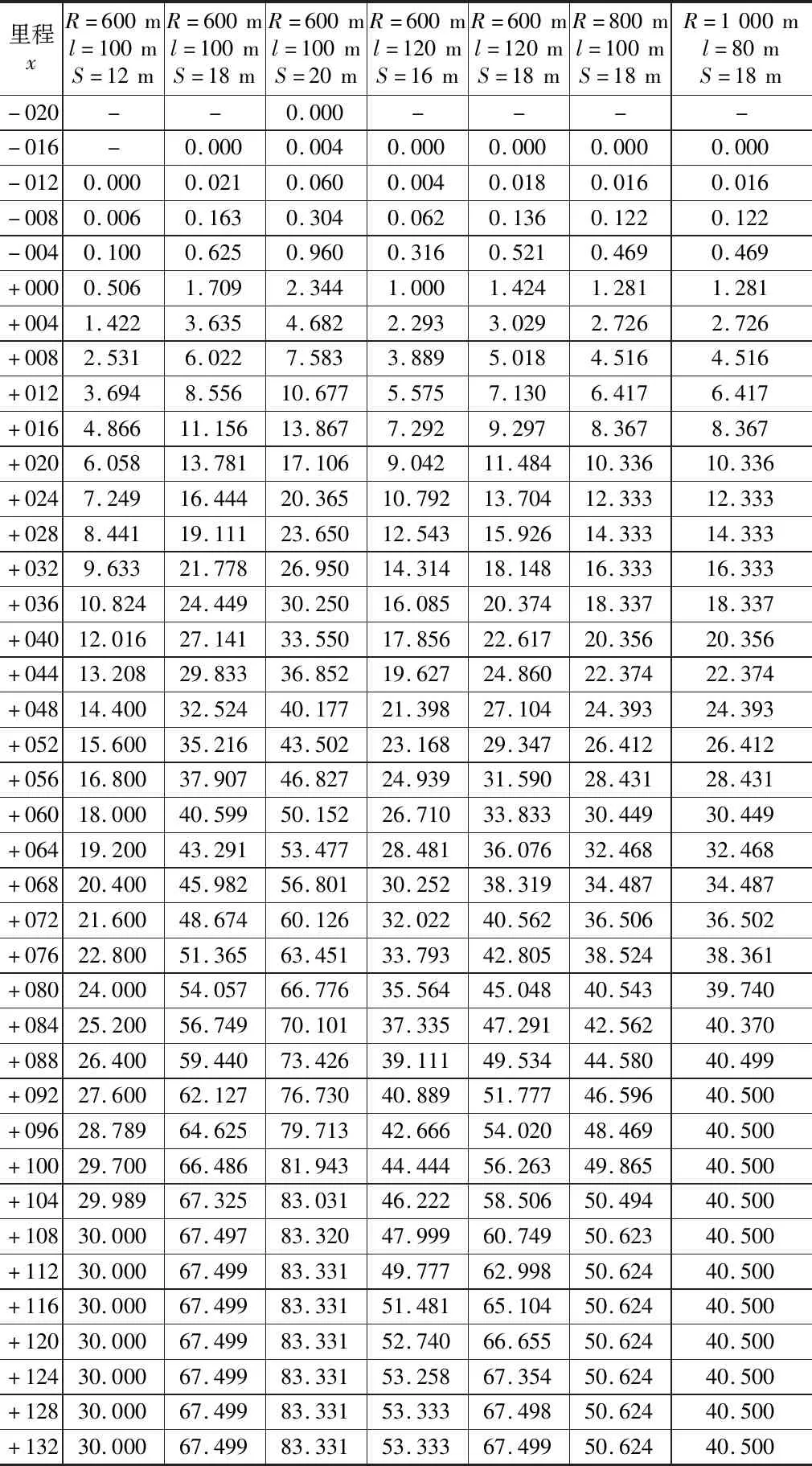
表7 R=600 m，S=12～24 m設緩和曲線時內側加寬值表(mm)

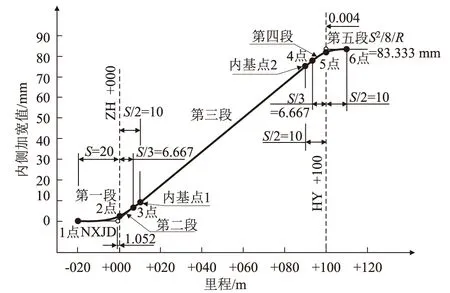
圖3 R=600 m，l=100 m，S=20 m設緩和曲線時內側加寬值示意圖

5.1.2 內側加寬值曲線特征分析

(1)內側加寬值曲線的交點

從圖3可以看出，設緩和曲線時內側加寬值曲線近似為反向曲線。經過對程序生成的內外側加寬值曲線圖形進行分析，中間一段可近似為直線。為便于分析，考慮平衡誤差以及適應短夾直線的計算條件，按ZH點后1/2倍定距點(命名為內基點1)、HY點前1/2倍定距點(命名為內基點2)作為擬合該直線的基點。內基點1、2間直線與0加寬值水平線、圓曲線段加寬值水平線有兩個交點，命名為NXJD和NSJD。從圖3可以看出，確定NXJD、NSJD坐標即可基本確定加寬曲線形狀。

圖3中內基點1里程取+010，內基點2里程 為+090。經測量程序導出的加寬值線圖形，下交點NXJD坐標為(-1.052,0)，上交點NSJD坐標為 (99.996，83.333)。

為分析NXJD和NSJD變化規律，測量得出其他計算條件下NXJD、NSJD坐標，如表8所示。

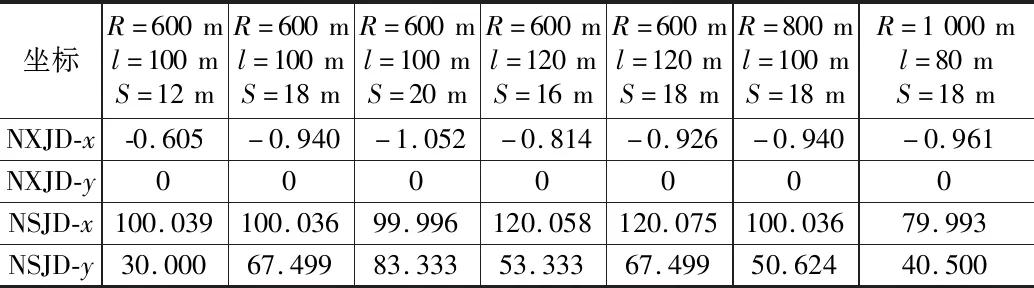
表8 內側加寬曲線NXJD、NSJD坐標值表

利用MATLAB軟件，結合其他計算條件圖解法數據，分析下交點x坐標關于定距和緩和曲線長的變化規律，得出x坐標可近似為：

(9)

上交點x坐標與緩和曲線長差距小于0.1，經驗證對加寬值曲線影響較小，上交點x坐標取為緩和曲線長。

xnsjd=1

(10)

(2)內側加寬值曲線特征點

結合參考文獻[3]，將內側加寬值曲線分為5段，特征點有6個，如表9所示。

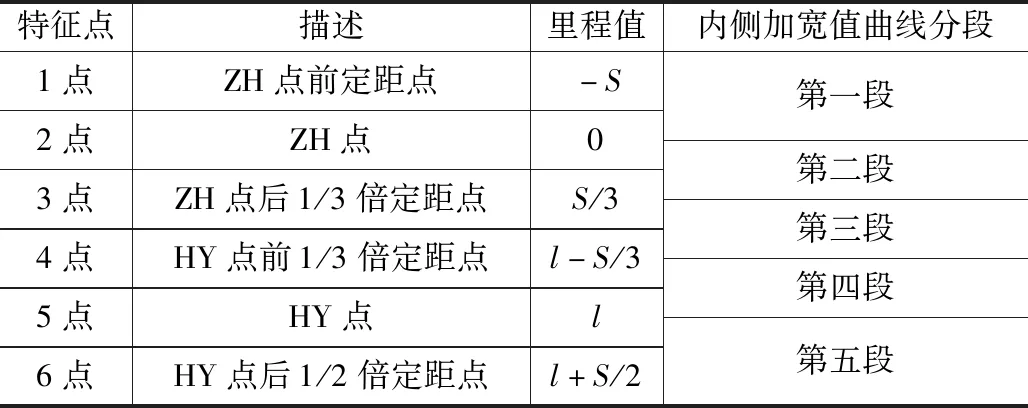
表9 設緩和曲線時內側加寬值曲線分段表

5.1.3 內側加寬值曲線分段分析

(1)第一、二段(從ZH點前定距點至ZH點、至ZH點后1/3倍定距點)

利用MATLAB、Excel軟件，對參考文獻[3]中兩段計算式進行驗證分析，經驗證與表7中各組合加寬值差值在 0.000 5 mm～-0.000 4 mm之間。整理得出則第一、二段加寬計算式為：

(11)

(12)

(2)第三段(從ZH點后1/3定距點至HY點前1/3定距點)

根據圖3及加寬曲線NXJD、NSJD坐標，采用內插法，得出第三段加寬式為：

(13)

經驗證，采用式(13)計算結果與表7各組合加寬值差值在0.322 mm～-0.120 mm之間。

(3)第四、五段(從HY點前1/3倍定距點至HY點至HY點后1/2倍定距點)

參考前述分析，第五段加寬計算式應較第四段簡單，因此先分析第五段。利用MATLAB軟件，對HY點至HY點后1/2倍定距點內側加寬值進行分析、按w=S2/8/R+a(x-l-S/2)3格式進行整理，如表10所示。

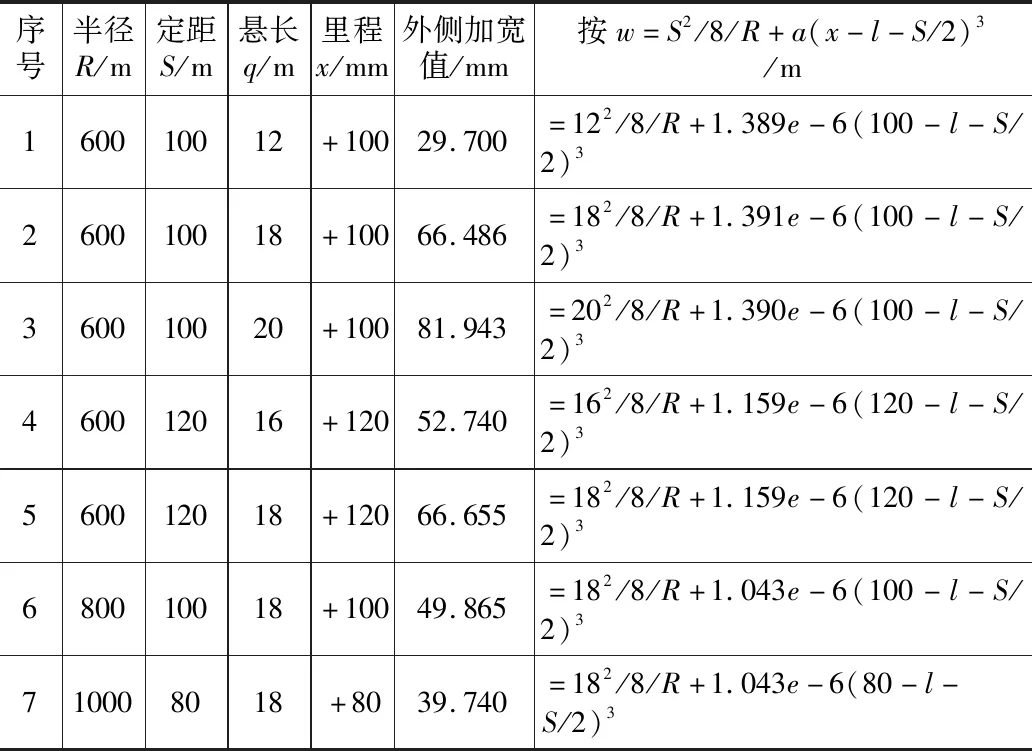
表10 不設緩和曲線HY點后1/2倍定距長點內側加寬值表

從表10可以看出，a值與定距無關，與R、l成反比，對a值進行整理，初步得a=1/(12Rl)。

第四段，利用MATLAB軟件，對HY點前1/3倍定距點至HY點內側加寬值進行分析、結合初擬第五段計算式，按w=S2/8/R+a(x-l-S/2)3+b(x-l)3格式進行整理，如表11所示。

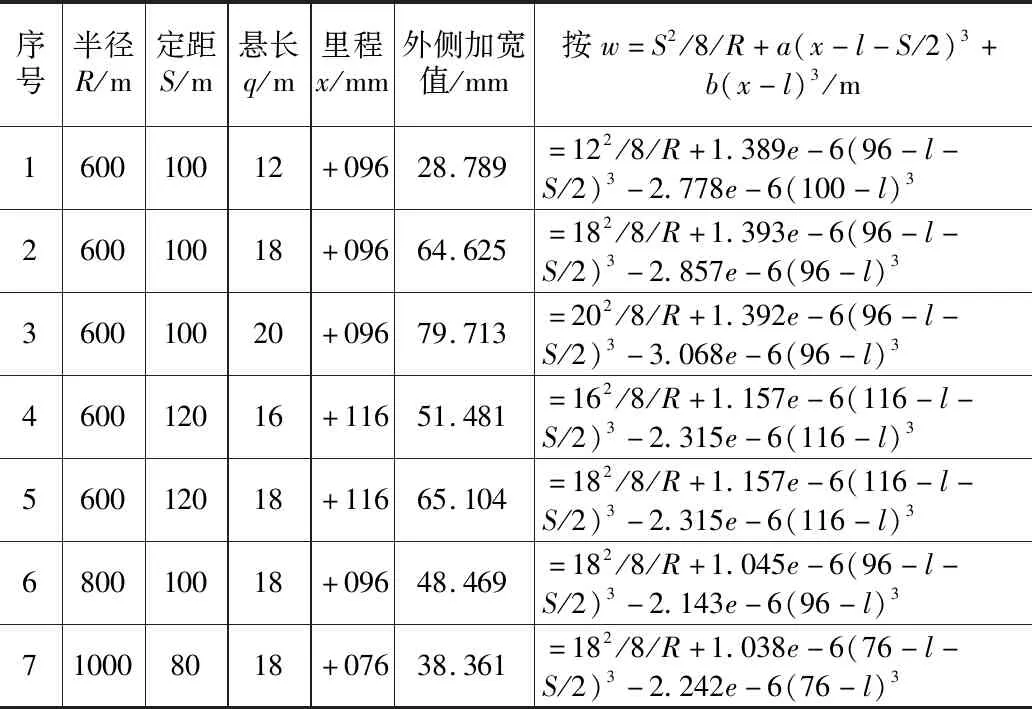
表11 不設緩和曲線HY點前內側加寬值表

從表11可以看出，a值與表10中a值基本相同，b值與半徑無關，約等于a值的-2倍，對b值進行整理，初步得b=-1/(6Rl)。

將上述a，b值進行第四、五段內側加寬值驗算，發現當半徑、緩長取值較小時誤差較大，如當R=200，l=20，S=18，x=14及20時，按該式計算加寬值為123.188 mm、187.313 mm，而圖解法計算加寬值為146.064 mm、188.344 mm，誤差值較大。說明a、b直接按與R、l取反比不嚴謹。因此利用大數據分析的方法，重新分析a，b取值。研究了半徑采用R=200、300，l=20～100，S=18時a，b取值，如表12所示。

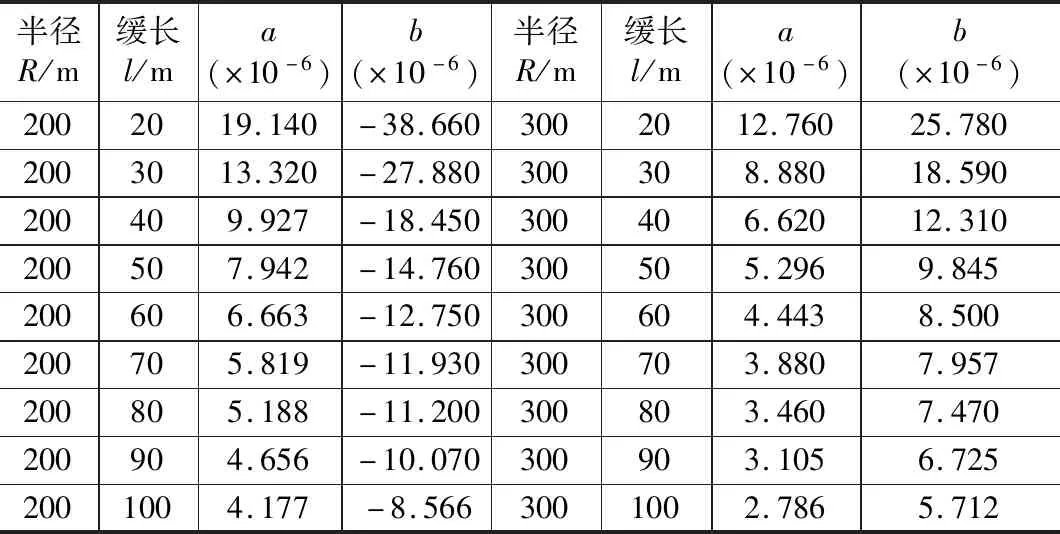
表12 設緩和曲線第四、五段a、b值表

利用MATLAB軟件，分析a、b值規律，得出a、b值與R成反比，與l成非線性遞減，b≈2a。擬合整理為：

(14)

則得出第四、五段加寬計算式：

(15)

(16)

經驗證，采用式(15)、式(16)計算結果與表7各組合加寬值差值在0.018～-0.007 mm之間。與R=200、300，l=20～100，S=18時各組合加寬值差值在0.929～1.043 mm之間

5.2 設緩和曲線時建筑限界曲線外側加寬

5.2.1 圖解法數據及外側加寬值示意圖

影響變量為半徑R、緩長l、車輛定距S及懸長q。通過圖解法數據，得出不同車輛尺寸、不同線路平面參數設緩和曲線時各點的外側加寬值，如表13所示。以R=600 m、l=100 m、S=18 m、q=4 m為例繪制設緩和曲線時外側加寬值示意圖，如圖4所示。

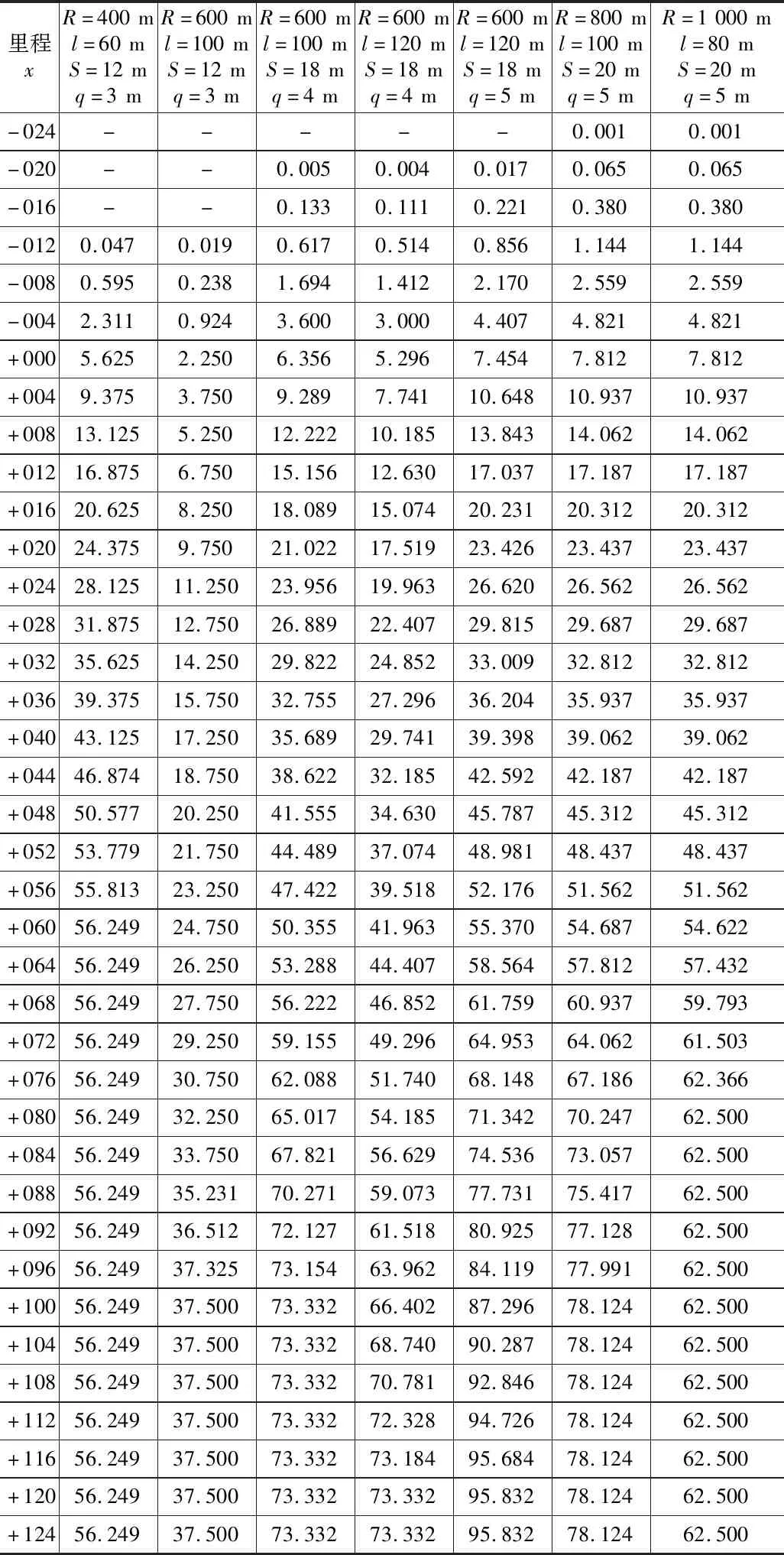
表13 設緩和曲線時外側加寬值表(mm)

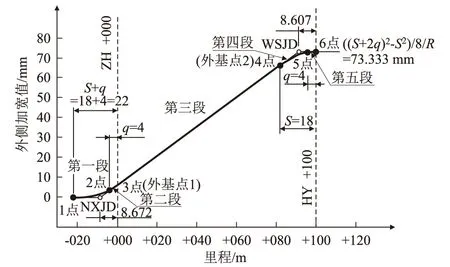
圖4 R=600 m，l=100 m，S=18 m，q=4 m設緩和曲線時外側加寬值示意圖

5.2.2 外側加寬值曲線特征分析

(1)外側加寬值曲線的交點

從圖4可以看出，設緩和曲線時外側加寬值曲線也近似為反向曲線,中間一段可近似為直線。與內側類似，按ZH點(命名為外基點1)、HY點前1倍定距點(命名為外基點2)作為擬合該直線的基點。下部和上部交點命名為WXJD和WSJD。

圖4中外基點1里程取為+000，外基點2里程取為+082。經測量程序導出的加寬值線圖形，下交點WXJD坐標為(-8.672,0)，上交點WSJD坐標為 (91.393，73.333)。

為分析WXJD和WSJD變化規律，測量得出其他計算條件下WXJD、WSJD坐標，如表14所示。

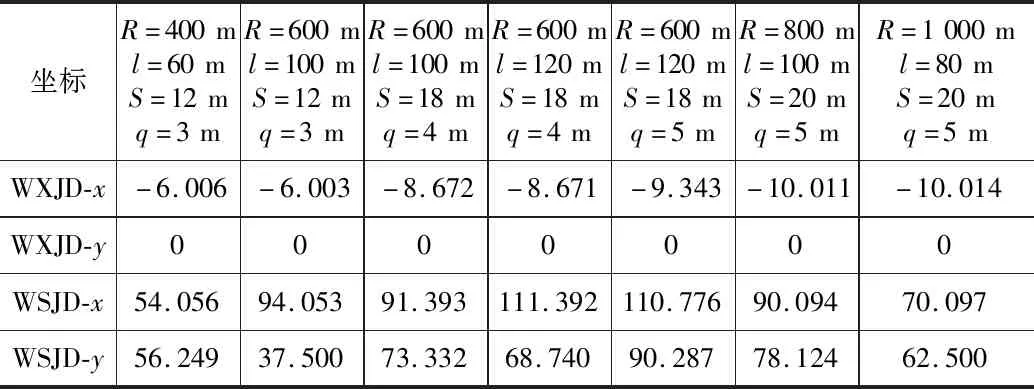
表14 外側加寬曲線WXJD、WSJD坐標值表

利用MATLAB軟件，結合其他計算條件圖解法數據，分析得出WXJD-x坐標可近似采用式(17)。上交點WSJD-x坐標可近似采用式(18)。

(17)

(18)

(2)外側加寬值曲線特征點

結合參考文獻[3]，將外側加寬值曲線分為5段，特征點有6個，如表15所示。

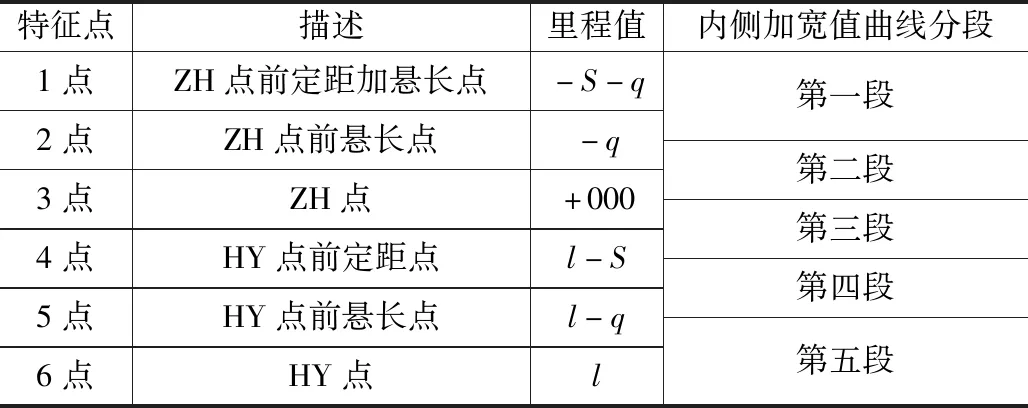
表15 設緩和曲線時外側加寬值曲線分段表

5.2.3 外側加寬值曲線分段分析

(1)第一、二段(從ZH點前定距加懸長點至ZH點前懸長點、至ZH點)

利用MATLAB、Excel軟件，對參考文獻[3]兩段計算式進行驗證分析，經驗證與表13中各組合加寬值差值在0.014 mm～ -0.209 mm之間。整理得出則外側加寬第一、二段加寬計算為：

(19)

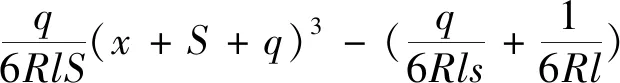
(x+q)3[-q≤x≤0]

(20)

(2)第三段(從ZH點至HY點前定距點)

根據圖4及加寬曲線WXJD、WSJD坐標，采用內插法，得出第三段加寬計算式：

[0≤x≤l-S]

(21)

經驗證，采用式(21)計算結果與表7各組合加寬值差值在0.322 mm～ -0.120 mm之間。

(3)第四、五段(從HY點前定距點至HY點前懸長點、至HY點)

與內側類似，先從第五段分析。利用MATLAB軟件，對HY點前懸長點至HY點外側加寬值進行分析，按w=((S+2q)2-S2)/8/R+c(x-l)3格式進行整理，如表16所示。

結合表16和其他計算條件圖解法數據，利用MATLAB對c值進行分析，得出c=1/(6Rl)。

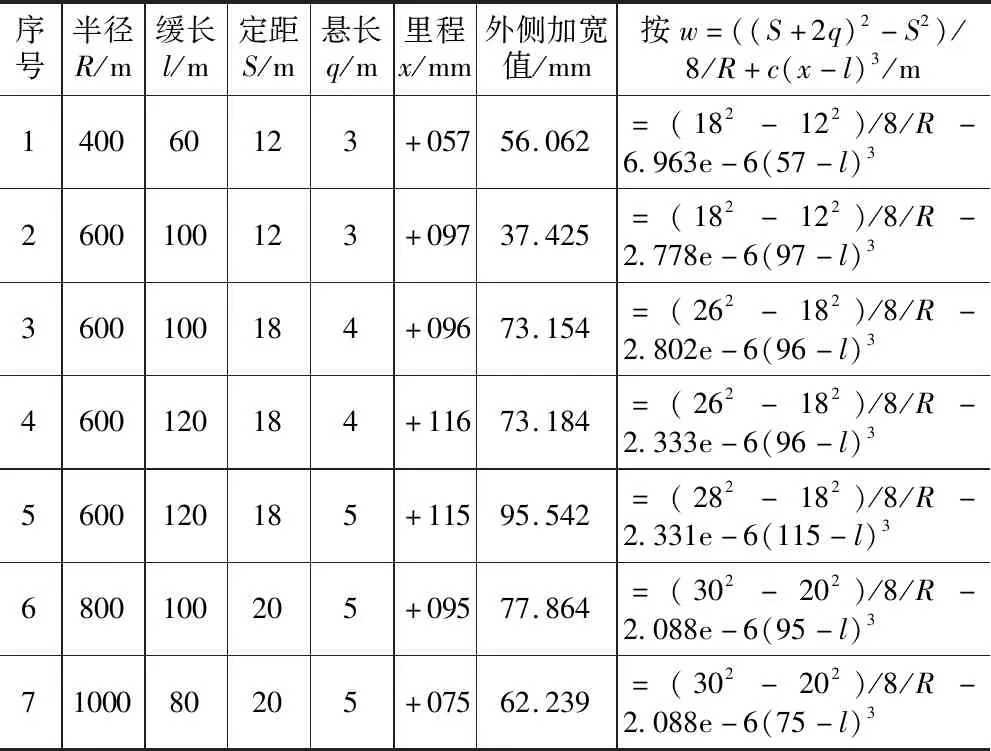
表16 設緩和曲線HY點前懸長點外側加寬值表

第四段，利用MATLAB軟件輔助，對HY點前定距點至HY點前懸長點外側加寬值進行分析、結合初擬的第五段計算式，按w=((S+2q)2-S2)/8/R+c(x-l)3+d(x-l+q)3格式進行整理，如表17所示。

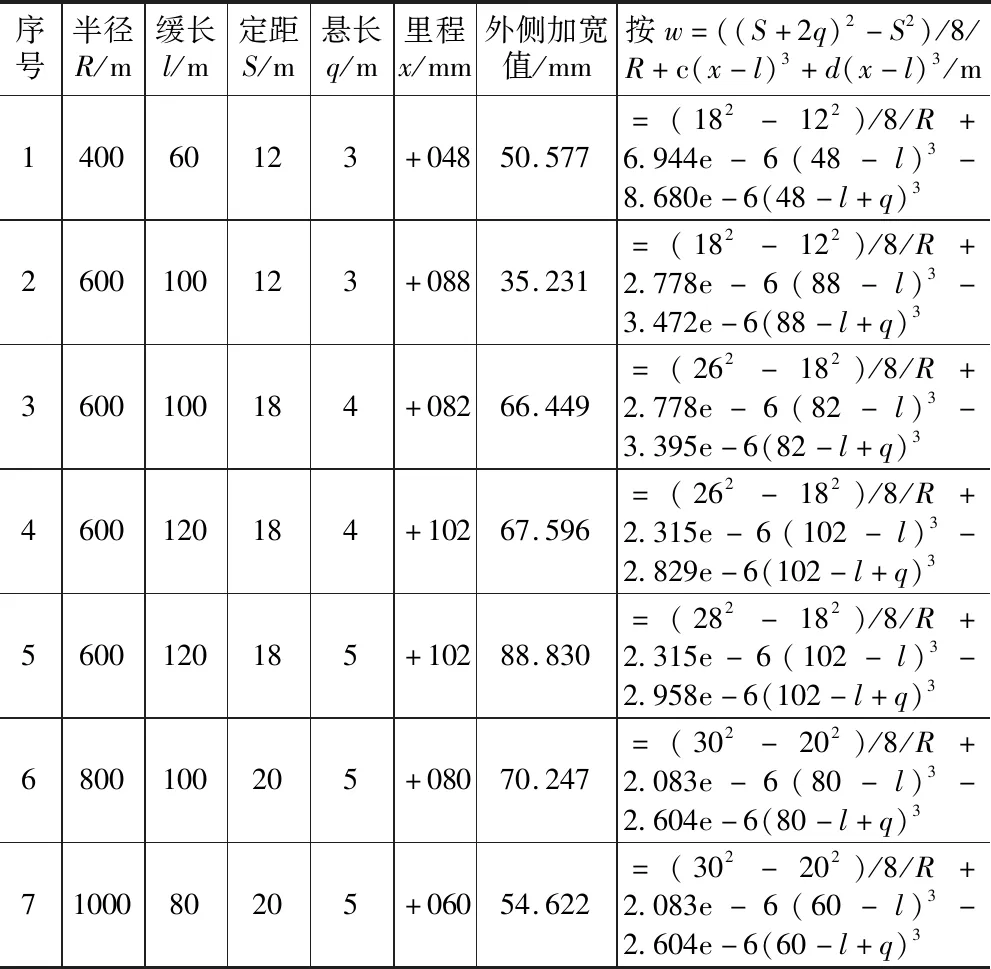
表17 不設緩和曲線HY點前定距點外側加寬值表

利用MATLAB軟件，分析c、d值規律，得出c、d值與R、l成反比，c與R、l成線性遞減，d與與R、l成非線性遞減。擬合整理為：

(22)

則第四、五段加寬計算式為：

(23)

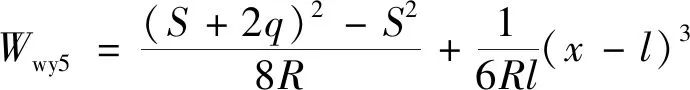
[l-q≤x≤l]

(24)

經驗證，采用式(23)、式(24)計算結果與表13各組合加寬值差值在0.019 mm～ -0.000 2 mm之間。

5.2.4 運動附加超高

曲線內側加寬還應考慮超高影響，在超高順坡段起點，除線路超高外，還存在著運動附加超高。其影響變量為車輛定距S、緩和曲線長l及超高值h。

結合參考文獻[2]，利用MATLAB軟件輔助，對既有資料進行整理，得出設緩和曲線時各點的計算超高(已包含運動附加超高)值計算式為：

(25)

(26)

6 結束語

本次研究利用計算機程序生成的不同計算條件建筑限界加寬值圖解法數據，繪制了不同車輛尺寸、不同線路平面參數的直-圓、直-緩-圓過渡段建筑限界曲線內外側加寬值示意圖，分析明確了各加寬值示意圖的特征，提出了各特征點計算方法。在研究借鑒參考文獻的基礎上，完善、提出了建筑限界曲線加寬通用計算式，并與圖解法數據對照，驗證了通用計算式的正確性。本次研究針對鐵道行業底層性、基礎性的技術問題，研究成果可以推廣至不同軌距鐵路、地鐵、市域鐵路等軌道交通領域。