基于相似度的蟻群聚類算法?
沈興鑫 楊余旺 肖高權 徐益民 陳響洲
(1.南京理工大學計算機科學與工程學院 南京 210094)
(2.湖南云箭集團有限公司 懷化 419500)
1 引言
聚類[1](Clustering)是一種重要的數據挖掘分析方法,主要目標是在海量數據中找出相似的數據并按照相似度分為不同的類,從而使得一個集群內的數據項彼此相似,不同集合中的數據盡量不同。從生物學到社會學再到計算機科學等眾多領域都存在相同的需求,因此聚類算法得到了廣泛的應用。
蟻群聚類(Ant Colony Clustering)是一種受蟻群啟發的聚類算法。意大利學者Dorigo M[2]在模仿螞蟻群體行為的基礎上提出了蟻群算法,根據蟻群的信息素機制尋找蟻穴和食物間的最短路徑,并有效地解決TSP問題。Deneubourg J[3]基于人工蟻群模型結合螞蟻的堆尸行為提出了聚類算法(Basic ant colony clustering model,BM)。Lumer E D和Fa?ieta B[4]在BM模型的基礎上改變螞蟻移動速度提出了LF模型,很好地解決了大數據量時的聚類問題。
相比于其他的聚類算法,蟻群聚類有以下幾個優點,如靈活性、魯棒性、分布性和自組織性。因此該算法被更多的人研究并改進。Bin W和Zhong?zhi S[5]研究了相似系數,并提出了一種更簡單的概率轉換函數。王慧和甘泉[6]加入了參數自適應調整策略,提高了蟻群聚類的準確性。喬少杰[7]研究了蟻群的分布式模型在文本聚類中的應用。Tan S C等[8]提出了一種簡化的基于螞蟻的聚類方法,該方法基于現有的基于螞蟻的聚類系統的研究。林金灼[9]結合了主成分分析方法(Principal Compo?nent Analysis,PCA),提高了蟻群的聚類質量。Tao等[10]重新定義了兩個數據對象之間的距離,并改進了螞蟻丟棄和拾取數據對象的策略,從而提出了一種改進的蟻群聚類算法。Xu X等[11]提出了一種約束螞蟻聚類算法,該算法嵌入了基于隨機游走的啟發式步行機制,以解決約束聚類問題。張夢佳[12]采用實時信息素更新規則,提高了蟻群聚類的收斂速度,同時提高了準確度。周峰[13]提出一種結合蟻群聚類和模糊均值聚類思想的聚類算法算法,該算法具有全局優化能力,優化了蟻群聚類易陷入局部最優的缺點。趙寶江[14]利用蟻群聚類算法來進行結構辨識,確定系統的模糊空間和模糊規則數,實現非線性系統的辨識,辨識精度高,可當作復雜系統建模的一種有效手段。
雖然以上方法優化了蟻群聚類算法,但是蟻群聚類前期收斂速度慢的問題未有效的解決。由于螞蟻隨機移動數據項的位置存在多次無效的移動,導致算法計算效率和準確性較低,對于復雜的工程,該問題更為突出。為克服這些缺點,本文提出了一種新的蟻群聚類算法,通過添加相似度矩陣將原算法中螞蟻隨機移動修改成按照相似度矩陣有目的地移動,螞蟻隨機關聯修改成有目的地關聯。通過實際數據集驗證了新算法的性能,并與先前研究中提出的蟻群聚類算法和其他算法進行了比較,驗證了新算法的有效性。
2 蟻群聚類算法
蟻群聚類算法是一種群體智能方法,受到蟻群堆積尸體和排序幼蟲行為的啟發而形成的一種聚類方法。因其靈活性、魯棒性、分散性和自組織性等特點被廣泛研究。
2.1 LF算法基本原理
在LF模型中,將螞蟻的尸體建模為需要聚類的數據項,螞蟻建模為在環境中隨機移動的代理,螞蟻移動的平面建模為一個具有邊界條件的二維網格。分散在平面中的數據項通過代理拾取、搬運和放下從而將相似的數據項放在一起。數據項的取放概率受到該數據項與鄰域內其他數據項的相似性和密度的影響,在拾取時,相似度越低越有可能拾取,相反,在放下時,相似度越高越可能放下。因此在網格上對數據項進行排列,使得相似度越高的數據項在平面上越靠近。
2.2 蟻群聚類算法模型
首先,將N個數據項隨機地映射到一個M×M的二維平面中,并將E只螞蟻分散到數據平面中并為每只螞蟻ei關聯一個數據項,即形成螞蟻到數據項映射:

其中E是螞蟻集合,N是數據項集合,F是螞蟻到數據項的隨機映射函數。
再計算出當前數據項與鄰域內其他數據項的相似度f(ei),相似度計算式(2)所示。

其中α是自定義的參數,用來調節螞蟻間的相似度。V定義了螞蟻的移動速度,vmax代表了最大速度,V隨機分布在[1 ,vmax]中。s是自定義的螞蟻的搜索長度。Neighs×s(r)代表位置r的周圍s×s面積。d( ei,ej)是ei和ej之間的距離。d( ei,ej)采用歐式距離,公式如下:
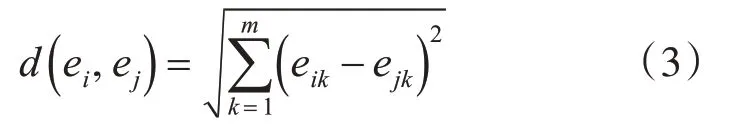
其中m是數據項的維度。
當螞蟻處于空載狀態需要拾起數據項時,按照如下公式計算拾起概率pp:
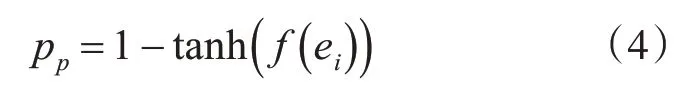
其中f(ei)是ei的相似函數,tanh(x)函數的定義如式(4)所示。

其中c為自定義的常量,用來調節算法匯聚的速度。
當螞蟻處于負載狀態需要放下數據項時,按照如下公式計算放下概率pd:
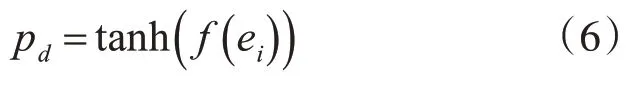
tanh函數和pp概率曲線圖如圖1所示。
在本模型中,螞蟻在拾起或者放下數據項后隨機移動,數據項與領域內的數據項相似度可能不高,因此下次被移動的概率又會增加,從而降低了聚類的速率。同時,當負載的螞蟻放下數據項或者空載的螞蟻沒有拾起數據項而需要重新關聯數據項時,數據項的關聯也是隨機的,增大了再次關聯的概率,導致聚類速率降低。

圖1 tanh函數圖和pp概率曲線圖
針對以上兩個缺點,本文在原有算法基礎上設計了相似度矩陣,讓螞蟻按照相似度有目的地移動,同時在螞蟻需要映射數據項時,根據相似度矩陣有選擇的映射,從而加快聚類的速度。
3 改進的蟻群聚類算法
傳統的蟻群算法移動蟻卵或者關聯蟻卵時都是隨機,存在無效移動與映射,導致聚類效率降低。改進的蟻群聚類算法在原有算法基礎上設計了相似度矩陣,螞蟻按照相似度有目標地移動,同時有選擇地映射到數據項,從而加快聚類速度。
3.1 算法原理
蟻群聚類通過螞蟻移動數據項,使相似度高的數據項在平面上盡可能靠近,從而形成聚類簇。在此過程中,將數據項移動到相似度高的區域附近可以大幅提高聚類速度。螞蟻因放下或者未能拾起數據項時需要重新關聯數據項。此時,當前數據項和鄰域的相似度較高,需要移動的概率較低,因此,關聯相似度低的數據項,增加操作次數可以提高聚類效率。
3.2 算法實現過程
3.2.1 建立相似度序列矩陣
首先計算每個數據項和其他數據項之間的距離。由于余弦相似度計算簡單、直接,對于單獨判斷兩個數據對象的相似度準確率高,因此本算法采用余弦相似度來計算數據項間的距離,其定義如下:
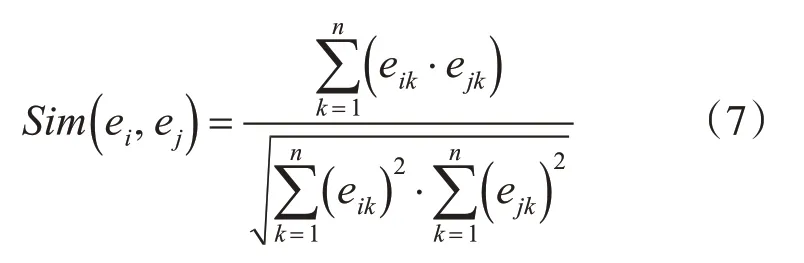
其中ei、ej表示兩個不同的數據項,eik、ejk表示不同數據項所代表的矢量坐標值,n表示數據項的維度。
然后對余弦距離標準化,形成相似矩陣(Simi?larity Matrix)。該矩陣是一個N×N的對稱矩陣,表示N個數據項兩兩之間的相似度,形如:
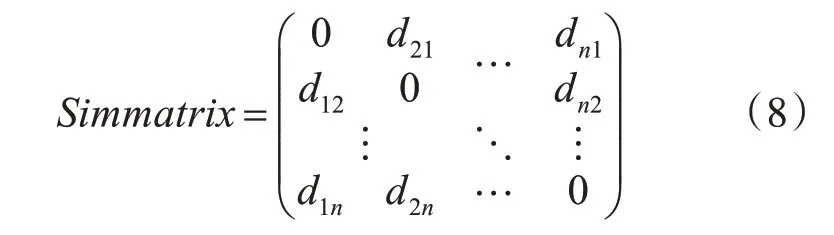
其中,dij是數據項i和對象j之間余弦距離的標準化表示。當數據項i和數據項j越相似,其值越接近0;相反,兩個數據項越不同,其值越接近1。
再以相似矩陣為基礎,以列為單位,按照相似度從高到地的順序進行排序,形成相似度序列矩陣,形如以下公式:

其中函數f(x)是以矩陣x為參數的快速排序函數,sij表示與第i個數據項相似度排序第j個的數據項的序號,sij∈(1…n)。數據項與該數據項的 相 似 度 最 高 ,因 此 [s11s12…sn1]=[1 2…n]。
3.2.2 提高螞蟻的移動目的性
在螞蟻移動數據項時,首先根據以下公式確定當前數據項的鄰域。

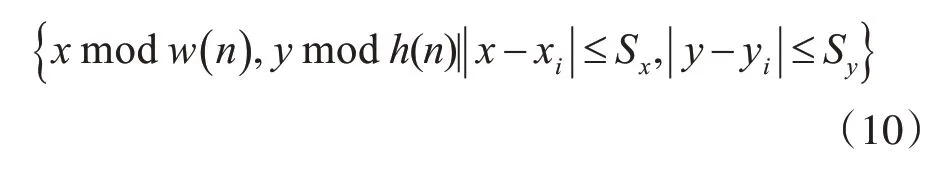
其中anti表示第i只螞蟻,位于( xi,yi),Sx和Sy分別代表該螞蟻水平方向和豎直方向的視野。數據項領域如圖2所示。
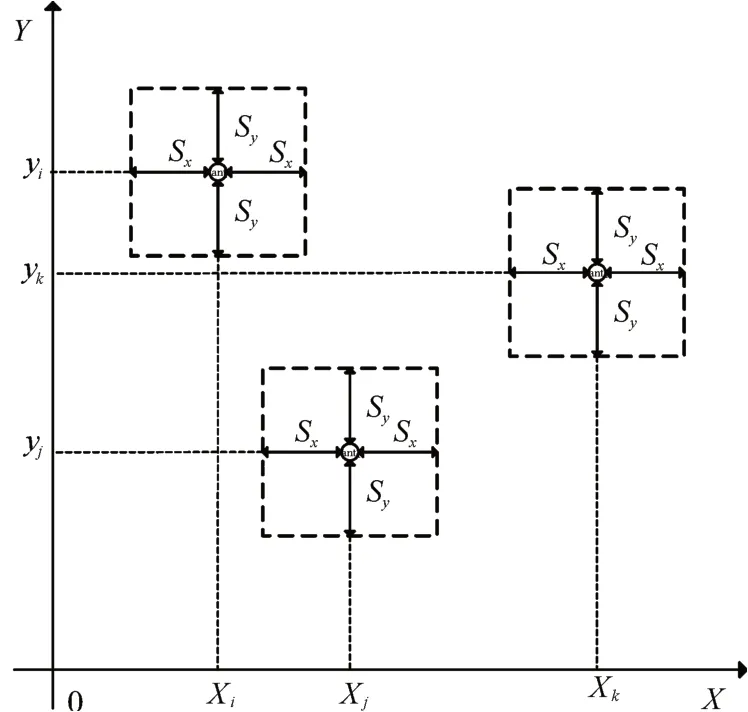
圖2 數據項領域范圍
然后確定鄰域中的數據項,即ej∈N( anti),再按照相似度序列矩陣找出鄰域中相似度最高的數據項,將當前數據項移動到該數據項附近。
Algorithm1:Similar Move
1)Input:Index of current spawn
2)Ouput:Index of most similar spawn
3)Calculate Neighbor Area(N(oi))
4)Get column i of Indexmatix
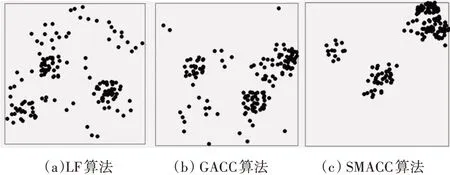
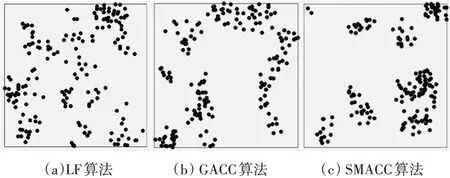
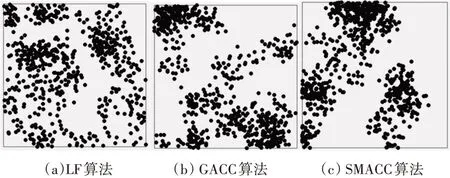
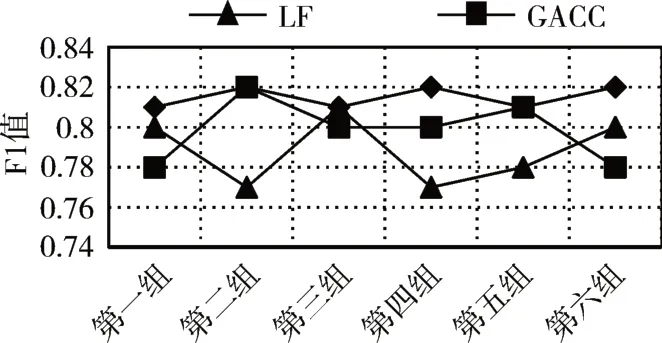
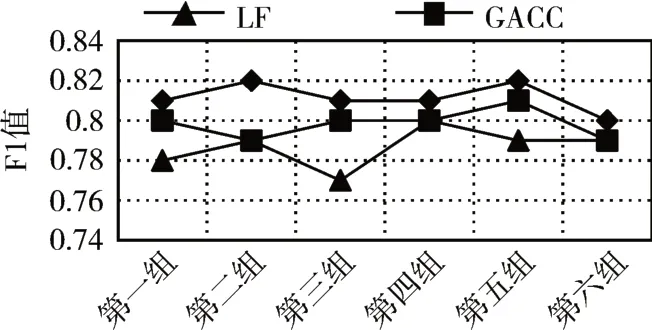
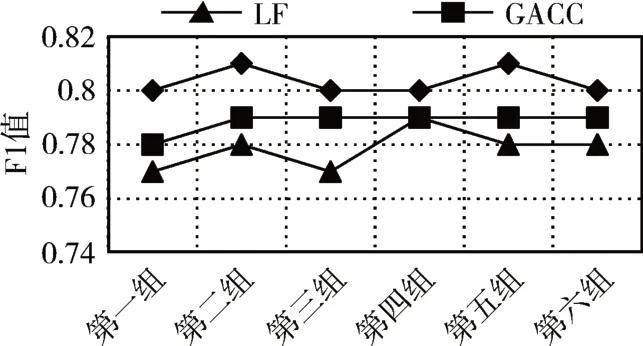
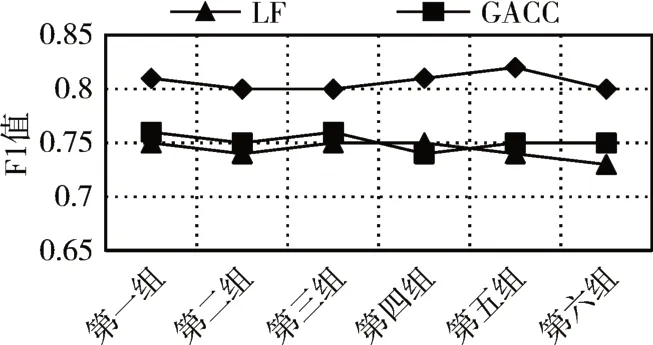
5)For j=1;j 6)k←Indexmatix[i][j] 7)If ok?N(oi) 8) Move oinearby ok 9) Return k 10) Else 11) Continue 12) End if 13)End for 14)Return Spawn number-1 3.2.3 增加關聯的目的性 按照相似度序列矩陣找到和當前數據項最不相似的數據項并映射到該螞蟻,偽代碼如下: Algorithm2:Dissimilar Mapping 1)Input:Index of current ant i 2)Output:Index of most dissimilar spawn k 3)Get column i of Indexmatix 4)For j=Spawn number-1;j>=1;j-- 5)k←Indexmatix[i][j] 6)If oknot occupied 7) Map current antito ok 8) Return k 9)Else 10) Continue 11)End if 12)End for 為驗證改進算法的有效性,本文設計了仿真實驗,通過不同數據集和不同算法的實驗結果對比,驗證了本算法的有效性。 實驗所用的數據集:本實驗采用了UCI數據集中最常用的Iris,Wine,Haberman,Balance-scale數據集,數據集的簡介如表1所示。 表1 樣本參數 本文的算法采用了相似度矩陣(Similarity Ma?trix)提高算法的聚類效率,記改進的蟻群聚類算法為SMACC(Similarity Matrix Ant Colony Clustering)。 用LF算法,文獻[15]中的GACC(GAnt Colo?ny Clustering)算法和SMACC算法對Iris,Wine和Haberman數據集進行聚類,在同樣迭代4000次的情況下,運行結果分別如圖3、圖4、圖5所示。由結果可以看出,對Iris,Wine和Haberman數據集迭代4000次后,SMACC算法聚類結果最明顯,GACC算法有明顯的聚類趨勢,而LF算法僅有聚類趨勢,這表明本算法相對其他兩種算法有較高的聚類效率。Balance-scale數據集的樣本個數遠大于其他數據集,在迭代4000次后很難比較聚類的效果,圖6是三種算法迭代10000次后Balance-scale數據集的聚類結果。結果可以看出,SMACC在大數據集的聚類效果明顯優于其他兩種算法。 圖3 Iris數據集 圖4 Wine數據集 圖5 Haberman數據集 圖6 Balance-scale數據集 Iris數據集和Wine數據集有相似的樣本個數,但Wine數據集的屬性個數遠大于Iris數據集的屬性個數。比較圖1和圖2可知,屬性個數增加,聚類效果有所降低。但是,由于SMACC算法采用余弦距離計算數據項間的相似距離,余弦距離更有利于區分高維度的數據項,因此,SMACC在高維度數據項的聚類效果遠優于其他兩個算法。在相同的迭代次數下,Iris數據集的聚類效果比Wine數據集的聚類效果好。 在一次迭代過程中,如果放下或者未撿起數據項的螞蟻數量占總量的90%時,表明聚類基本完成。三種算法分別在四種數據集上收斂時的六次平均迭代次數如表2所示。 如表2所示,使用相同數據集時,SMACC的平均迭代次數明顯小于其他兩種算法,該結果表明本算法有效地提高了聚類速度。Balance-scala數據集中,SMACC的迭代次數遠小于其他兩種算法,說明該算法更適用于大數據集的聚類。 表2 平均迭代次數比較 F-measure從查準率和查全率綜合的角度衡量聚類算法的結果。其一般形式如式(2)所示: 其中,β是查準率和查全率的權重比,P是查準率,R是查全率。 本文采用F1值比較四種數據集上三種算法的聚類效果,結果如圖7~10所示。 圖7 Iris數據集 圖8 Wine數據集 圖9 Haberman數據集 圖10 Balance-scale數據集 比較三種聚類算法對四種不同數據集的F1值,GACC和SMACC算法與LF算法的聚類效果總體相似,但GACC和SMACC略好于LF算法。隨著數據集中樣本數量的增加,三種算法的F1值總體有所下降,由于SMACC算法在螞蟻移動的過程中有目的地移動,所以數據簇中相似度總體比較高,所以在Balance-scale數據集中F1值明顯高于LF和GACC算法。同時,由于蟻群聚類是基于群體行為的聚類方法,隨著數據量的增加,聚類結果的波動也減小。圖8中,由于數據的維度增加,樣本的區分度有所降低,但SMACC采用余弦距離作為相似距離,所以F1值略高于其他兩個算法。 蟻群聚類是一種利用群體智能的聚類算法,其靈感來自蟻群聚集其尸體的行為。該算法具有魯棒性強,適合分布式等優點,但是因為螞蟻隨機移動數據項而造成多次無效移動以及資源浪費。針對該問題,本文設計了相似度矩陣,使螞蟻在相似度矩陣的指導下有目的地移動和關聯,從而加快聚類速度。 仿真實驗中,對比了本算法和其他兩種算法對UCI數據集中四個實際數據集(Iris,Wine,Haber?man,Balance-scale)的聚類性能。結果表明,新的蟻群聚類算法在保證聚類精度的基礎上,能夠以較高的速度解決聚類問題,同時具有很好的計算穩定性。但是SMACC依然存在局部優化的問題,在接下來的工作中希望通過參數的動態調整來解決該問題。4 實驗結果與分析
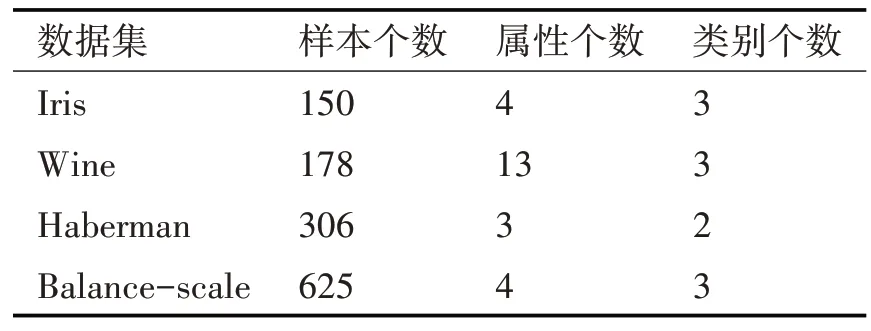
4.1 實驗環境與實驗數據集
4.2 實驗結果與分析



5 結語

