基于雙曲切比雪夫逼近的光譜模板構造?

于 苗 蔡江輝 楊海峰

（太原科技大學計算機科學與技術學院 太原 030024）

1 引言

郭守敬望遠鏡（LAMOST）［1～4］是一種特殊的反射施密特望遠鏡，有效孔徑為3.6m～4.9m，焦距為20m，視場為5°，其焦面上可防止4000根光纖，因此在一次曝光中LAMOST可以同時觀測到4000條光譜。在恒星和星系的科學研究方面，LAMOST有著巨大的研究前景和價值。LAMOST巡天得到的光譜復雜多樣，有各種類型的光譜。對天體光譜的分析首先需要進行光譜的自動識別，因此研究恒星自動識別與分類方法具有重要意義［5～6］。

恒星自動識別與分類系統的正確率和可信度取決于恒星光譜模板庫的質量。目前常用的恒星光譜模板庫主要有MAFAGS［7］、MARCS［8～11］、Kurucz理論模板庫［12］。MAFAGS模板庫是一套步長較細的網格光譜數據，MARCS模板庫只包含F、G、K型星模型并且對冷星更適用，Kurucz模板庫是恒星大氣模型網格數據。共包含約9561個模型，大部分為正常恒星模型。該恒星理論光譜庫的構建分成兩部分包括大氣模型的計算和理論光譜的合成，即從大氣模型的輸入量：表面有效溫度Teff、表面重力加速度g、元素豐度（［M/H］）到光譜的輸出量：流量（x），波長（λ），這是一個非常復雜的非線性映射過程。

上述三種恒星模板庫的構造方法適用于所有來源的恒星光譜來構造相應模板庫。然而將其運用于LAMOST巡天得到的恒星光譜數據時并不能很好地對恒星光譜數據進行自動識別和分類。基于以上缺陷，韋鵬［13］等在構造了包含183條模板光譜，61個不同的子類型的適用于LAMOST的恒星光譜模板庫，該模板庫是韋鵬從約100萬條LA?MOST DR1恒星光譜數據中經過一系列操作篩選出來的，被廣泛應用于LAMOST光譜分類工作中，該模板庫的構造方法復雜。

上述現存的恒星理論光譜模板庫構造方法較為復雜，給恒星光譜自動識別和分類帶來了一定的困難。因此本文提出了一種基于切比雪夫雙曲線逼近的恒星光譜模板構造方法。該方法首先將光譜數據分段，分為多個小光譜段，得到具有多個波段并提取波長流量信息，然后依據波長流量信息基于切比雪夫雙曲線逼近提取每類光譜數據特征譜線的形狀特征，最后將提取出的光譜數據特征譜線的形狀特征與標準光譜特征譜線比較。

2 理論基礎

2.1 函數逼近與一致逼近

函數逼近［14］就是用簡單函數逼近已知的復雜函數。通常步驟為首先通過復雜函數在有限點集上給定函數值，再在包含該點集的區間上用公式給出函數的簡單表達式。即對于函數類A中給定的函數（fx），要求在另一類較簡單的便于計算的函數類B中找到一個函數p（x），使p（x）與（fx）的誤差在某種度量意義下達到最小。函數類A通常是區間［a，b］上的連續函數，記作C［a，b］，而函數類B通常為n次多項式等。

將函數逼近問題中的逼近函數與給定函數之間的逼近方式給出一種定義，換言之，一致逼近［15］是度量連續函數（fx）和逼近多項式p（x）之差的一種標準，即對于區間［a，b］上的連續函數（fx），對于給定的任意小正數ε>0，存在多項式p（x），使不等式

成立，則稱多項式p（x）在區間［a，b］上一致逼近于函數（fx）。顯然，如果精確度越高，即ε越趨近于0，則用來逼近的多項式p（x）的次數一般也越高。

2.2 切比雪夫逼近

切比雪夫逼近［16～17］是切比雪夫基于一致逼近提出的確定逼近的最快的多項式的方法。切比雪夫逼近的思想是：不讓逼近多項式的次數n趨向于無窮大，而是先把n固定。

定義（偏差）：次數不超過n次的實系數多項式的集合為pn，p(x)∈pn，f(x)∈C[a，b]，f(x)與p(x)的偏差定義如下：

定義（切比雪夫逼近）：對于函數f(x)，在pn中尋找一個多項式p*n(x)，使其滿足：

此時p*n(x)對f(x)的偏差和其他任一p(x)對（fx）的偏差比較時是最小的，我們稱p*n(x)為f(x)在［a，b］上的切比雪夫逼近。

在切比雪夫逼近中，逼近多項式p*n(x)的選擇很多種，包括代數多項式、三角多項式以及有理分式函數等。

3 基于切比雪夫雙曲線逼近的分段式模板構造方法

3.1 切比雪夫雙曲線逼近

顯然，切比雪夫逼近定義是用一個多項式逼近一個連續函數。將切比雪夫逼近的思想擴展到用一個多項式逼近一組連續函數，得到該組連續函數的切比雪夫逼近多項式，可描述為對于區間［a，b］上的l個連續函數f1(x)，…，fl(x)，p*n(x)為該組連續函數的切比雪夫逼近，則p*n(x)滿足：

此時，pn*(x)對每一個連續函數fi(x)的偏差和不超過n次的實系數多項式的集合pn上其他任意多項式p(x)與fi(x)的偏差相比時都是最小的。

因為任意曲線都可通過擬合近似表示得到函數表達式，因此將每個連續函數fi(x)看作區間［a，b］上的曲線Si(t)，那么對于l個連續函數求切比雪夫逼近就轉化為對l條曲線求最佳逼近。在此基礎上，切比雪夫雙曲線逼近最初來源于上述對多條曲線的切比雪夫逼近。其中心思想是將對多條曲線的切比雪夫逼近等價到對兩條曲線的切比雪夫逼近上，這兩條曲線分別是最大值曲線和最小值曲線。此時式（4）可轉化為

每一條曲線與最佳逼近之間的偏差最小簡化為最大值函數或最小值函數與最佳逼近之間的偏差最小。其中，Smax(t)為該組曲線在區間［a，b］上的最大值曲線，其定義為

Smin(t)為該組曲線在區間［a，b］上的最小值曲線，其定義為

S*(A，t)為該組曲線的切比雪夫雙曲線逼近。得到S*(A，t)的方法是先用函數來假設該最佳逼近，然后求出系數的值，具體的函數表達式就可知了。用函數形式表示最佳逼近，假設最佳逼近的形式表示為

此外，為求解式（5）引入一個變量z，該變量z表示任意一條曲線與最佳逼近間的最小差值，其表示為

此時，解決上述最佳逼近函數的問題轉化為解決線性規劃的問題。該線性規劃可表示如下：

目標函數為

約束條件為

通過求解該線性規劃問題可得最小偏差z和最佳逼近函S(A，ti)。

3.2 算法描述

基于切比雪夫雙曲線逼近的分段式恒星光譜模板構造方法，將所有光譜按類分組，相同類型的恒星光譜視作一組并提取各組光譜的波長和流量信息，對每一組光譜數據進行分段，使每一組光譜分為具有若干段的同類型光譜組，對于各段的波長流量信息，將波長作為自變量，流量作為因變量，得到相關曲線。對每一條曲線進行歸一化，再分別通過式（6）、（7）計算該組曲線的最大值曲線和最小值曲線。引入變量z，用多個未知參數和多項式基的代數和的形式表示該組光譜的切比雪夫雙曲線逼近，用最大值曲線、最小值曲線和式（9）定義變量z，運用式（10）、（11）線性規劃的方法在每段光譜上做切比雪夫雙曲線逼近，得到各組的整體態勢。具體步驟如下。

算法：基于切比雪夫雙曲線的恒星光譜模板構造方法

輸入：LAMOST數據集D，光譜類數X，分段長度T，光譜維度W

輸出：各類恒星光譜模板

1）對每條光譜歸一化

2）將每條光譜按T分段，總段數為S

S=「W/T?

3）for x=1 to X do

4） 根據式（6）、（7），計算得到Smax（t）and Smin（t）

5）for s=1 to S do

6） 根據式（10）、（11），計算min z，S(A，ti)

7） end for

8）end for

9）該組光譜的切比雪夫雙曲線計算完成

本文的算法內容主要包括兩個部分，第一部分是光譜數據分段，第二部分是在每類已分段的光譜數據實現切比雪夫雙曲線逼近。光譜數據分段的時間復雜度為O（n），實現切比雪夫雙曲線逼近的時間復雜度為O（n2），算法的整體時間復雜度為O（n2）。

4 實驗分析

在1臺Inter（R）core（TM）i7-6500U@2.50GHz筆記本電腦，Windows 7操作系統中使用Python語言在PyCharm平臺實現了基于切比雪夫雙曲線逼近的分段式恒星光譜模板構造方法。

4.1 實驗數據選擇

本實驗主要在LAMOST DR5恒星光譜數據上進行實驗得到適用于lAMOST恒星光譜數據的恒星光譜模板。每條LAMOST光譜數據都有相應的波長和流量信息，波長范圍在3700～9000。本實驗選取原本由pipeline分類得到的A、F、G、K、M五類恒星光譜數據，信噪比不低于20。具體數量如表1所示。

表1 恒星數據情況

4.2 實驗結果與分析

4.2.1 各類恒星模板光譜

本實驗在上述數據集上進行操作，得到的各類恒星模板光譜如圖1～5所示。

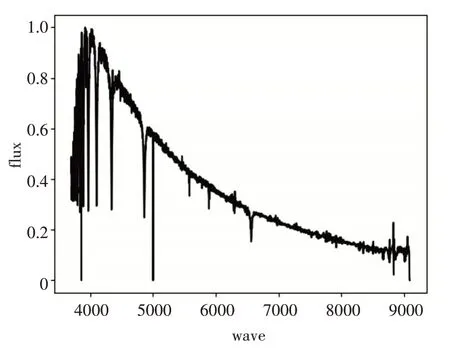
圖1 A型光譜模板

圖2 F型光譜模板

圖3 G型光譜模板

圖4 K型光譜模板

圖5 M型光譜模板

4.2.2 整體態勢分析

從上述模板光譜中看出不同類型的恒星光譜模板譜整體走勢是不相同的，具有明顯的差異性。具體分析圖1～5，從A型光譜到F型光譜再到G型光譜，大致來看藍端高紅端低并且峰值逐漸向紅端移動。K型光譜，已經變成紅端高藍端低，再到M型光譜完全變成紅端與藍端的差距加大，并且藍端變得非常高。上述計算所得的各類恒星光譜模板譜的整體態勢與互相過渡變化滿足各類光譜整體走勢理論。因此，本文所提方法構造的恒星模板譜具有可信度。

4.2.3 與其他光譜模板的比較（數量）

該實驗在A、F、G、K、M五種恒星光譜數據情況下實驗具體選取了A1IV、F0、G0、K0、M0共5個子類的數據。在現行的韋鵬等構造的183恒星光譜模版中，子類A1IV的模板譜數量為4，子類F0的模板譜數量為4，G0的模板譜數量為2，子類K0的模板譜數量為3，子類M0的模板譜數量為10。每一個子類的模板譜的數量皆大于1條。然而運用上述方法對每一個子類恒星光譜都可以得到唯一一條模板譜。模板譜數量減少，大大提高了恒星自動識別和分類的效率。

5 結語

本文提出了一種切比雪夫雙曲線逼近的分段式恒星光譜模板構造方法，該算法采用將整條的光譜劃分為多段子光譜，提取其相應的波長和流量信息，并得到光譜的最大值曲線和最小值曲線。通過切比雪夫雙曲線逼近利用偏差的最小值z和最佳逼近的代數表達式，最大值和最小值曲線通過線性規劃的方法得到一組曲線的切比雪夫雙曲線逼近，將其作為該類恒星光譜的模板譜，最終通過該方法得到恒星光譜的模板譜。采用恒星光譜數據集驗證了方法的有效性。本文下一步的研究方向為考慮如何能提高算法的運行速度，加快實現各子類恒星光譜模板譜的構造。