應用譜域迭代算法計算理想導電腔體的RCS

郭華昌，汪平平，史俊峰

（西安愛生技術集團公司，陜西西安，710065）

0 引言

精確預估目標的RCS特征在現代軍事上有著非常重要的意義[1-3]。大量研究結果顯示，各類腔體結構（噴氣式發動機的進氣道、尾噴口，背腔天線以及機體上的縫隙，接口等）對飛行器的總體的RCS特征有非常顯著的貢獻[1]。

對于電大尺寸開口腔體的電磁散射計算，目前常用的方法以高頻射線方法為主，但其精度和效率較低。近年來，譜域迭代算法的研究有了很大進展[4]，該方法利用Fourier變換把三維空間場的場量變成譜域中的一維空間場量，然后用傳輸線理論，可以求解復雜腔體的電磁散射問題。譜域迭代法的實質是將空間域的積分方程變換為譜域中的代數方程，對于待求解的場量或電流，如果假設的分布和實際的分布比較接近，并滿足邊界條件，那么所需要求解的矩陣方程的階數很小，很方便獲得近似解或數值解。

本文應用譜域迭代方法，對理想導電腔體結構的電磁散射進行了有效的分析。論文重點討論了腔體邊緣繞射場的計算方法，給出了計算類矩形截面的鏡像源法和計算任意截面的幾何繞射理論方法，為了改進后者計算精度，引入了等效電磁流方法。所得結果與其它方法（模式混合法）結果吻合很好。

1 自由空間場的平面波譜分解

在無源空間中，電場和磁場滿足標量波動方程，給定的場量可以通過傅立葉變換轉換為譜域的表示形式[6]：

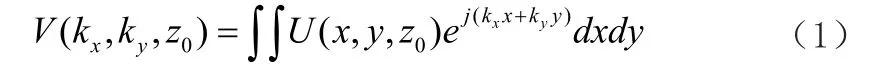
2 等效電磁流法處理任意截面形狀腔體的口徑場

電磁波在腔體中傳播時是經過有限尺寸的口徑向內輻射，當照射場照射到腔體口徑邊緣時，會在口徑面上產生邊緣繞射場，對耦合進口徑面的場產生影響，所以計算時必須采取措施將邊緣繞射場計算在內。

對于任意口徑形狀的腔體而言，腔體曲邊緣繞射會使繞射射線產生焦散區，而幾何繞射理論的主要缺點就是不能計算焦散區的場，一致性幾何繞射理論只解決了使繞射場算式在幾何光學陰影邊界過渡區中保持有效地問題，但它仍不能用以計算繞射射線焦散區的場。本文在此引入等效電磁流法（MEC）[6]來計算腔體口徑邊緣所產生的繞射場。MEC修正了GTD方法不能計算繞射射線焦散區場的缺點。

根據高頻場的局部性原理，將MEC方法應用在曲邊緣上時，將腔體口徑邊緣的局部等效為直劈。這一直劈的兩個面和構成曲劈的兩個曲面在繞射點相切，且等效直劈的邊緣和曲邊緣在繞射點相切。則在口徑邊緣任一點Q的等效邊緣電磁流為：

將入射場同口徑邊緣繞射場相疊加，就可得到整個入射平面的入射電場。

3 波譜在腔體中的傳播

決定模型形狀的因素主要有腔體幾何形狀的復雜程度，光滑度，以及所擁有的計算機資源和所要求的精度。根據腔壁截面形狀的變化，需將腔體形狀近似分解為由一系列矩形波導組成的階梯波導，從而建立計算模型。

以圖1所示的簡單腔體模型為例介紹波譜在腔體中傳播的模式以及迭代過程。圖中虛線為實際腔體邊界，粗實線為近似矩形腔體邊界。為了調整不同截面口徑上的場的采樣，并且保證滿足導體邊界上的邊界條件，在相鄰兩段不同截面的波導之間，要對前一段波導的終端場進行修正。

圖1 波譜在腔體內的傳播

迭代過程可分為兩個部分。第一部分是第一次傳播過程，亦即一次迭代。第二部分為高次迭代。當波譜從口徑場向終端傳播時（前向傳播），如圖3中所示，在第一個接口處，第二部分截面增大，這時，將截面上1，2兩部分的入射場記為零。當波譜傳輸到第二個接口時，第三部分截面減小，記錄（1），（3）兩部分的反射場的采樣。當波譜從終端向口徑場傳播時（后向傳播），在第一個接口處，將在前向傳播過程中記錄的（1），（3）兩部分采樣計入波譜，在第二個界面處，記錄1，2處的反射波采樣，以備下次迭代時使用。當波譜傳輸到入射口徑面時，第一次迭代完成。這時已可以計算后向散射場，但由于傳播過程中，腔體截面發生變化處會產生多次反射，因此應對其進行高次迭代，記錄每次迭代對口徑場出射波的貢獻，以提高精度。

經過多次迭代，口徑場的精度達到要求后，就可利用kiechhoff積分算出遠區散射場，公式如下：

4 典型腔體結構的算例

應用本文算法，計算了一個S形腔體模型的RCS，計算中，采用了等效電磁流法計算口徑繞射場。本文結果與模式混合法的結果進行了比較，在正負20度范圍內吻合很好。腔體模型參數及其RCS計算結果如圖2所示。

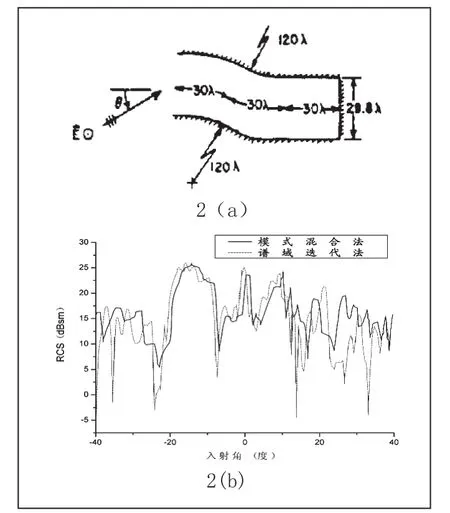
圖2 S形腔體模型及其RCS計算結果（TM極化）

本文方法在一定角度范圍內具有了很好的精度，在工程上，可以進行很實用的預估；一般數值方法（如有限元，矩量法等）計算量很大，計算時間和占用內存的消耗量大。采用本文的譜域迭代法計算上述模型，在PIV3.0臺式計算機上，計算一個數據點僅需時8分鐘左右。顯著提高了計算效率，具有較高的實際應用價值。

5 結束語

譜域迭代法作為一種高效的低頻方法在電磁領域中有著廣泛的應用。本文對在任意截面形狀腔體中應用譜域迭代法計算理想導電腔體RCS的方法進行了探討。通過對一種典型的S形腔體的計算，驗證了方法的正確性。