微壓力表測量不確定度的評定及CMC表達探討
黃健勇
(廣東省臺山市質(zhì)量技術(shù)監(jiān)督檢測所,廣東臺山,529200)
0 引言
根據(jù)《計量標準考核規(guī)范》中明確提出的規(guī)定,分析評定微壓力測量表的不確定度;按照《法定計量檢定機構(gòu)考核規(guī)范》中的內(nèi)容,測量機構(gòu)需要將參與項目的全部量程與參數(shù)都需要計算相應的校準測量能力。考慮到微壓力測量表對于不確定度的評定與對校準測量能力的表達之間的關(guān)系較為不清晰。因此,將在實例測量、判定的基礎(chǔ)上,對二者展開工作的過程與需求進行闡明。
1 計量標準考核中的測量不確定度
在相應的規(guī)則章程中,對微壓力測量表的不確定度評定的定義是:基于計量檢定規(guī)定,通過計量標準,將典型的被評定或被校準的對象進行檢定后得出的不確定度。因此,在不確定度的評定中,還應將被測對象與測量影響進行納入,且必須保證被測對象具備一定的代表性與典型性,微壓力表在計量標準考核中測量不確定度的評定與常規(guī)條件下的不確定度評定具有一定的重復性,但是在實際的評定與分析中,應明確以下兩點:第一,如果計量標準能夠?qū)Χ鄠€參數(shù)進行測量,需要分別提供每個參數(shù)的微壓力表測量不確定度評定流程;第二,如果被測對象的分度值或不確定度不同,那么需要采取的評定方式也應進行調(diào)整匹配,假設(shè)測量點之間沒有較大差距,則可以提供典型的不確定評定過程,在實際的評定中,應針對項目的特征對其進行不確定度的測量[1]。
2 實驗室的校準測量能力
為保證實驗室或相關(guān)機構(gòu)開展校準測量能力的正確評定,首要任務(wù)是明晰校準測量能力的應用含義。對于校準測量能力的定義是:向用戶提供高質(zhì)量的校準測量,通過因子k=2或者置信概率為p=0.95的擴展不確定度來表達。此外,在實驗室中也可以將校準測量能力稱作最佳測量能力。專業(yè)的歐洲認可組織對于校準測量能力的闡述是:實驗室的校準測量能力在其認可標準范圍內(nèi),當用于規(guī)定、實現(xiàn)、保存一個或多個值的測量標準處于理想狀態(tài)下,并將其進行常規(guī)校準時,能夠?qū)⑽毫Ρ頊y定不確定度降至最低;當用于測量數(shù)值的儀器處于理想狀態(tài)下,并將其進行常規(guī)校準時,能夠?qū)y量儀器的不確定度降至最低。基于以上定義可知,微壓力測量表的校準測量能力主要應用于特定、具體的量的測算中,即測量結(jié)果。因此,微壓力表校準測量能力是求測量結(jié)果的不確定度,屬于連接測量結(jié)果的參數(shù)。
從理論層面上來看,校準測量能力是實驗室將不確定度最低的“理想被校”通過測量后得出的最小測量不確定度。但是,“理想被校”非常少見。為解決這一問題,通常會采取以下兩種被校方式進行替代。第一種,選取穩(wěn)定性與重復性強的被校來替代“理想被校”。在校準測量能力評定的過程中,將樣本標準差進行歸并;第二種,選取穩(wěn)定性非常強并對測量結(jié)果分散性貢獻只由分辨力誤差產(chǎn)生的被校替代“理想被校”。在校準測量能力評定過程中,將不確定度的貢獻部分轉(zhuǎn)變?yōu)榉直媪y量結(jié)論不確定度的貢獻部分。
在測量短時間的分散性貢獻時,可以將量塊、砝碼、電阻等相對平穩(wěn)的被校進行忽略。以上被校與理想被校之間的差距微乎其微。因此,可以將以上被校的校準測量能力與不確定度劃等號。對于校準測量能力的表述方法與測量不確定度的評定方法相對一致。例如:當不同量程或測量點的被校結(jié)論不一致時,就不能應用同一個被校值,應根據(jù)不同分段,提供不同的校準測量能力,或給予校準能力范圍,同時,提供典型量程及測量點的校準測量能力[2]。
3 微壓力表測量不確定度評定和校準測量能力表達分析
3.1 標準不確定度評定
首先,確定DWRER4級的(0-60)Pa且分度值為2Pa的為微差壓表為評定設(shè)備,在此基礎(chǔ)上開展不確定度的評定工作;其次,將標準補償式微壓計產(chǎn)生的不確定度進行分量,并記為U1。微壓計生成的不確定度分量主要由二等微壓計的壓力誤差產(chǎn)生,此微壓計的不確定度分量的分布是較為均勻的,符合B類不確定評定,由標準補償式微壓計產(chǎn)生的分量誤差范圍是±0.8Pa;最后,將由重復性測量產(chǎn)生的不確定度進行分量,并記為U2。當標準器處于30Pa狀態(tài)時,對微壓力表進行10次重復性試驗,將十次測量結(jié)果進行平均值計算,結(jié)果為:=30.08Pa。單次的檢測標準差的計算過程及計算結(jié)果如公式1所示:
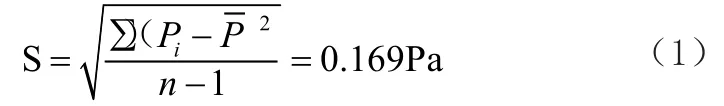
而平均值的實驗標準偏差的計算過程及計算公式如公式2所示:
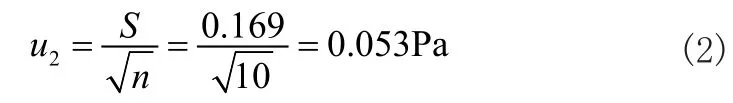
通過測量值進行估讀與引入的不確定度進行分量,記為U3。遵照測量標準,對微差壓表進行數(shù)值讀取時,應讀至標準分度值的處。結(jié)合指針深度與人工視覺誤差,對于誤差的估讀應按照不可靠性的分度值估計。此誤差的分布屬均勻形態(tài),因此,讀數(shù)的標準不確定度分量的計算過程及結(jié)果如公式3所示:
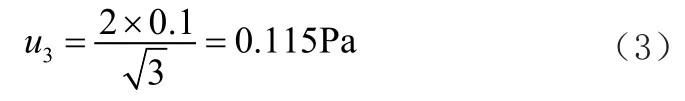
考慮到重復性計算產(chǎn)生的誤差,只保留最大的影響分量u3。
3.2 合成標準不確定度
在對合成標準的不確定度展開計算時,各個影響分量均應選取其中較大的數(shù)值。計算過程如公式4所示:
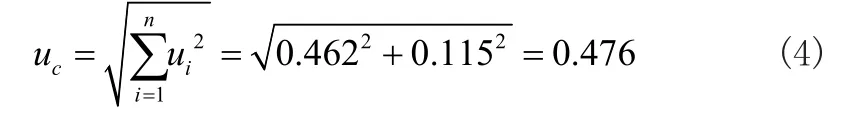
對標準不確定度的計算進行擴展時,首先需要確定k的取值,當k=2時,將不確定度擴展為:

3.3 微壓差計標準裝置校準的不確定度評估
根據(jù)相關(guān)規(guī)程,常規(guī)校準應做到對微差壓表中的全部測量點進行校準,允許誤差與之前一致,且儀表的分度值的量程范圍也不存在變化,從而確定不確定度的值為1.0Pa。
當校準壓力表的等級與分度值出現(xiàn)差異時,不確定度的分量u2與u3均會出現(xiàn)一定的不同。考慮到儀表分度值過大導致重復性降低的原因會間接影響不確定度關(guān)于分度值的函數(shù)[3]。結(jié)合標準儀器的允許誤差及校準點,可以確定:當校準點為0-1500Pa時,不確定度的表達方程為;當校準點為1500-2500Pa時,不確定度的表達方程為此公式滿足規(guī)程條件,公式中d代表被校準儀器的分度值。
3.4 校準測量能力的表達
結(jié)合以上測量不確定度的評定過程與內(nèi)容,DWYER微差壓表是補償式微壓計標準裝置的理想被校微壓力表。因此,校準項目的校準測量能力為:校準點處于0-1500Pa階段時,校準測量能力的不確定度的表達為;準點處于1500-2500Pa階段時,校準測量能力的不確定度的表達為。
4 結(jié)語
綜上研究證實,計量標準考核中,微壓力表測量不確定度的評定是對典型被測對象開展校準時得出結(jié)論的不確定度,此不確定度必須具備一定程度的代表性與普遍性。校準測量能力是全部測量結(jié)果中最小的不確定度,反映的是標準條件下的最高測量水平。

