Temperature and doping dependent flat-band superconductivity on the Lieb-lattice?

Feng Xu(徐峰) Lei Zhang(張磊) and Li-Yun Jiang(姜立運)

1School of Physics and Telecommunication Engineering,Shaanxi University of Technology,Hanzhong 723001,China

2Institute of Graphene at Shaanxi Key Laboratory of Catalysis,Shaanxi University of technology,Hanzhong 723001,China

Keywords: flat-band superconductivity, strong electron–electron interaction, superfluid weight, Berezinskii–Kosterlitz–Thouless(BKT)transition temperature

1. Introduction

Flat bands can be realized in the bipartite lattice, and a simple bipartite lattice featuring a strictly flat band is the Lieb lattice (Fig. 1(a)). It is a line-centered square lattice consisting of three atoms (A, B, C) which tight-binding dispersion is characterized by three band branches, and the middle energy band is a strictly flat bandEk=0.[8]Some theoretical works on the Lieb lattice focus on the ferromagnetic properties; the celebrated flat-band ferromagnetism was first studied by Lieb.[8–11]The studies about superconductivity on the Lieb model show that the high density of states enhances the superconducting critical temperature for fixed interaction strength,[7,12–16]while its topological properties are another interesting topic.[17–20]On the experimental side,the Lieb lattice has been realized using ultracold atoms,photonic lattices and also electronically.[21–23]

Another interesting flat band system is the twisted bilayer graphene. The surprising superconducting state in the twisted bilayer graphene is relevant to flat bands, which arouses new interest in flat-band superconductivity.[1–5,24]There is another simple way to get flat-band superconductivity in graphene by including periodic strain.[25–27]As these systems are twodimensional, they cannot undergo a conventional phase transition to a superconducting state owing to thermal fluctuation.The superconducting critical temperature is determined by the Berezinskii–Kosterlitz–Thouless temperature rather than the vanishing of the superfluid weight.[28–30,36]Therefore, it is crucial to examine the BKT transition on the Lieb model with a strong correlation to understand superfluid in the ultracold atoms or the superconductivity in the high-Tcsuperconductors.

Fig. 1. (a) The Lieb lattice and its unit cell, The sublattice in the unit cell are labeled by τ =A,B,C. The thick lines represent internal bonds hopping energy (1+κ)t, while the thin lines represent external bonds hopping energy (1 ?κ)t. The mean feild parameters χ and ?used in this paper are set as shown, χ is related to the bond order,?is related to the superconducting order, and the d-wave symmetry of the superconducting order is used. (b)–(c) The energy dispersion as a function of quasimomentum for κ =0(b)and κ =0.2(c). The middle band is strictly flatEk,0=0 for any κ while the upper and lower band has a gap

In this paper,we investigate the superconducting properties of Lieb lattice in the strong electron–electron correlation limit based on thet–Jmodel using the Gutzwiller renormalization mean-field method. The hole-doping and temperaturedependent superconductivity has been shown. Similar to hightemperature superconductivity in the CuO2planes,the superconducting region can be divided into the under-doped region and the over-doped region. The superconducting order amplitude increases linearly with doping level in the lightly doped region in the zero-temperature limit,showing almost irrelevant to electron–electron interaction strength because of the main dependence on the hole-doping level.We obtain the superfluid weight and BKT transition temperature for the d-wave superconducting state on this system. It is shown that the BKT transition temperature is much lower than the gap-opening temperature in the lightly doping level. This phenomenon characterizes the pseudogap state in high-temperature superconductors. As a comparison, the superfluid weight and BKT transition temperature in the optimal hole-doping level have been given. The BKT transition temperature has the same order as the energy gap and superfluid weight disappeared temperature.The BKT transformation temperature versus hole-doping level shows a similar tendency as the doping-dependent superconducting order in the zero-temperature limit. The prominent characteristic in flat-band superconductivity is the linearly increasing relation between superconducting critical temperature and the coupling strength, and we show the BKT transition temperature linearly increases with the electron–electron interaction strength.The effect of the staggered hoping parameter is discussed in the end. It remarkably reduces the superconducting region and the superconducting order in the zerotemperature limit. This paper is organized as follows. In Section 2,we describe the basic theoretical model and Gutzwiller renormalization mean-field method along with the formulation for computing the superfluid weight and the BKT transition temperature. In Section 3, we present our numerical results and discuss their physical meanings. Finally, some conclusions are drawn in Section 4.

2. Model and methodology

We study the extendedt–Jmodel on the Lieb lattice(see Fig.1(a)),governed by the following Hamiltonian:

The d-wave superconducting state has been considered in our work,so the mean-field order on they-direction is considered as shown in Fig.1(a),and the superscriptνindicates that these quantities are related to the physical order parameters. The superconducting order parameter is given by?=gtij?νij,and the bond order is also be rescaled. This project is similar to the slave-boson method, where?νequivalents to the average of spinon pairing operators. We perform a discrete Fourier transformation to the mean-field Hamiltonian with

whereψnkandEnkare the eigenfunction and eigenvalue of the mean-field Hamiltonian,kBis the Boltzmann constant,andTis temperature.

To obtain the superfluid weight, we examine the current response to a vector potential with linear response theory.[33,34]In the presence of the vector potentialAx(r,t)=Ax(q)exp(iqr ?iωt),the linear current is given by

and the kinetic energy density associated with thex-oriented link at positionris given by

The current–current correlation function is then given by Since the superfluid densityns(T) is obtained by numerical calculating, it is equivalent to the definition in terms of the stiffness of the superconducting order parameter in the thermodynamic potential.

3. Results and discussion

As mentioned above,we can achieve the strong constraint of forbidding double occupancy of two electrons on the same site using Gutzwiller factors, then study the superconducting properties of Lieb-Lattice on the mean field level.In our work,the pair field?νrepresents the local electron pairing order,and bond orderχνis the kinetic hopping term. We first show the superconducting order amplitude versus hole-doping level in the zero-temperature limit with various electron–electron coupling strengths in Fig.2. Here we chooseκ=0,which shows no energy gap between the upper and lower energy band in the normal state and the mean field values?ν1=?ν2, χν1=χν2according to the symmetry. There are two distinct regions for different hole-doping levels analogous to hole-doped dependent in the high-temperature superconductivity in the CuO2planes. The physical superconducting order linearly increases with the hole-doping levelδfor various electron–electron coupling strengths in the under-doped region. The doping levelδis defined asδ=δA+δB+δC; whenδ=0, the flat band is half filled, and whenδ=1, the flat band is empty. The superconducting order amplitude mainly depends on the holedoping level, so there is almost no difference with various electron–electron coupling strengths. The optimum doping level increases with the effective attraction strength between electrons and the maximum value of superconducting order.The superconducting region conspicuously reduces with the enhancement of the Hubbard interactionU, and the superconducting order rapidly declines with the doping level in the over-doped region.In particular,it should be noted that the superconducting order includes the contributions from all energy bands;however,the middle flat energy band plays an essential role.

Fig. 2. The superconducting order near-zero temperature varies with the hole-doping level δ, and κ =0 shows no energy gap between the upper and lower energy band in the normal state. The superconducting order is dominated by the hole-doping level when δ ≤0.038,and they linearly increase with δ with various Hubbard interaction U. Up to a maximum value, the superconducting order increases with the doping level,after that,rapidly decreases with it. The superconducting region decreases with the effective attraction strength J=4t2/U between pair electrons.

The enigmatic pseudogap state in high-temperature superconductors has long been recognized as a central puzzle in the research of cuprate superconductivity. It is widely proved that the pseudogap opens below a temperature much above the superconducting transition temperature in the under-doped region. We obtain the superfluid weight and BKT transition temperature with the help of linear response theory. The temperature-dependent physical orders in the lightly doping levelδ=0.03 withκ=0,U=4tare shown in Fig.3(a),and the superconducting order ?decreases with temperature increasing.In Fig.3(b),we show the superfluid weight as a function of temperature and get the BKT transition temperature. It is found that the superfluid weight decreases almost linearly with temperature due to the quasi-particles energy spectrum being gapless. The BKT transition temperature is determined by the intersection of2ns(T)/m?with 8kBT/π. The BKT transition is noteworthy lower than the temperature of the superfluid weight disappearance. As shown in Fig. 3, the gap opening temperatureT?is much higher than the superconducting critical temperatureTBKTwith ratioT?/(TBKT)≈10. The considerable disparity betweenT?andTBKTis similar to the pseudogap state in the high-temperature cuprate superconductors and may be used to understand the anomalous behavior of the superfluid weight in the high-Tcsuperconductors. The status for the optimum doping levelδ=0.086 withU=4t,κ=0 has been shown in Fig. 4 as a comparison. The critical temperature of the superconducting order is almost equal to the temperature of the superfluid weight disappearance.

Fig.3. (a)The superconducting order and the bond order evolution as a function of temperature at the lightly hole-doping level δ =0.03,U =4t,κ =0.(b)The superfluid weight decreases with the temperature and the BKT transition temperature point.

Fig.4. (a)The superconducting order and the bond order evolution as a function of temperature at the optimal hole-doping level δ =0.086,U=4t,κ=0.(b)The superfluid weight decreases with the temperature and the BKT transition temperature point.

The BKT transition temperature versus the hole-doping levelδis shown in Fig.5(a). Clearly, it exhibits a dome-like shape in resemblance to the superconducting dome observed in the high-Tccuprate superconductors and a recent similar situation discovered in the twisted bilayer graphene. The superconductivity emerges fromδ=0.01, the BKT transition temperature near zero under this doping level,and there is no physical realistic superconducting state under this condition.It is in accord with the consensus that there is no superconductivity in a strong correlation system near the half-filled.The superconducting critical temperatureTBKTincreases with the doping level in the under-doped region,while it decreases with the doping level in the over-doped region. The flatband superconductivity in this system is very different from other flat band systems;its superconducting region with holedoping level is much smaller than twisted bilayer graphene and strained graphene. This significant difference is caused by the strong ferromagnetic fluctuation on the Lieb lattice even under hole doping; however, the magnetic fluctuation in the twisted bilayer graphene and strained graphene is suppressed rapidly with the increase of the hole-doping level.As shown in Fig. 5(b), The BKT transition temperature linearly increases with the effective electron–electron attractive interactionJ=4t2/Ufor the strong Hubbard interaction fromU=4ttoU=6t. The linear relationship betweenTBKTandJis a characteristic of the flat-band superconductivity in contrast to the relation for the critical temperatureTc～e?1/gin the conventional superconductors. Even in the presence of the strong and repulsive correlation effect,the flat-band superconductivity is a potential route to high-temperature superconductivity.

Fig.5. (a)The BKT transformation temperature versus hole-doping level δ with U =4t,κ =0. (b) The BKT transition temperatures linearly increase with the coupling constant with δ =0.06,κ =0,U =4t to 6t.

Finally,we discuss the staggered effect in the lattice with the staggered hoping parameter on the superconducting state in the zero-temperature limit. Clearly,the superconducting region remarkably dwindles withκ=0.2. The main relationship between the superconducting order and the doping level is the same as the symmetry condition(κ=0);however,the superconducting state disappears with the maximal doping levelδ=0.029. The superconducting order is much smaller than the symmetry case with three orders of magnitude as shown in Fig.6,and the staggered hoping parameter makes the mean field value?1/=?2, χ1/=χ2. The superconducting state on the staggered Lieb lattice is restricted and hard to realize.

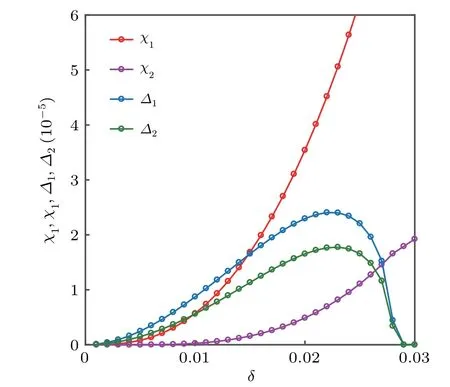
Fig.6.The superconducting order and the bond order in the zero-temperature limit versus the hole-doping level δ with staggered hopping parameters κ =0.2,U =4t.

4. Conclusion

In summary, we have shown the d-wave superconducting state on the Lieb lattice with a flat-band spectrum in the normal state in the strong electron–electron correlation limit.The superconducting order amplitude mainly depends on the hole-doping level and increases with it for various electron–electron coupling strengths in the lightly doped region, but rapidly decreases with doping level after reaching its maximum value. The hole-doping dependent superconducting properties of Lieb lattice are similar to the case in the cuprate superconductors. We study the thermal behavior of superfluid weight and get the BKT transition temperature which is used as the superconducting critical temperature because this system is two-dimensional. The conspicuous difference between gap opening temperatureT?andTBKTin the under-doped region is helpful to understand the enigmatic pseudogap state in the high-temperature superconductors. The dome-like shape of the BKT transition temperature versus hole-doping level is shown in resemblance to the superconducting dome observed in the high-Tccuprate superconductors and twisted bilayer graphene. The BKT transition temperature depends linearly on the electron–electron interaction strength,which shows the flat band plays a dominant role in the superconducting state on the Lieb lattice. The staggered effect on the lattice remarkably reduces the superconducting region. Lastly, a highly tunable Lieb lattice can be realized with ultracold gases in the experiment, and our results can examine and promote the understanding of the anomalous behavior of the superfluid weight in the high-Tcsuperconductors. The flat-band ferromagnetism brings strong ferromagnetic fluctuation on the Lieb lattice even under hole doping, so we will consider the ferromagnetic effect on the superconductivity under strong electron–electron correlation in future work.

Acknowledgement

We thank professor C.Y.Mou for the fruitful discussions.