基于Morris法的供水管網全局靈敏度分析

黃樂烽 杜坤 宋志剛 盧慢 董云程 許丁

(1.昆明理工大學建筑工程學院 昆明 650500； 2.云南省設計院集團有限公司 昆明 650000)

0 引言

供水管網模型可以模擬管網系統在一系列工況下的運行狀態，是實現供水系統現代化管理的重要工具。當在管網模型基礎上進行分析和設計時，比如模型校核、管徑優化設計以及監測點布置等，模型輸出結果存在不確定性，可能影響決策的有效性，部分原因是輸入參數的不確定性。不確定的輸入參數包括節點流量、管道阻力系數以及閥門狀態等。對大型供水管網進行分析時，眾多的參數意味著高維的輸入空間，對問題的求解需要大量計算資源。已有研究表明[1-2]，管網模型分析結果主要受部分關鍵參數的影響。因此，通過靈敏度分析辨別關鍵參數，重點圍繞關鍵參數進行分析，可有效降低問題復雜性和減少工作量。

靈敏度分析定性或定量評估輸入參數的不確定性對模型輸出結果的影響，可輔助基于模型進行的分析和設計。靈敏度分析包括局部靈敏度分析(LSA)和全局靈敏度分析(GSA)。LSA可以分析參數變化對模型輸出的局部影響，在供水管網研究領域應用較多。BUSH C A等[3]通過求導法計算參數靈敏度矩陣，用于優化管網水壓監測點布置。吳雙利等[4]利用有限差分法研究管道摩阻變化對水壓的影響，只對關鍵管道進行校核。與LSA相比，GSA是在整個參數定義域內，評估輸入參數單獨作用及交互作用對模型輸出的影響，更適用于非線性的管網模型。全局靈敏度分析方法主要有多元回歸法、Morris法、傅里葉幅度靈敏度檢驗法、Sobol’法等[5]。其中的 Sobol’法近年開始應用于供水管網領域。信昆侖等[6]利用Sobol’法對管網模型中的管道摩阻進行靈敏度分析，選取靈敏度較大的管道進行校核，其余管道摩阻則取經驗值，提高了校核效率且達到了預定的精度要求。在管網多目標優化設計方面，FU G等[1]以兩個基準管網為例，利用Sobol’法篩選出對管網性能影響較大的管道，再對問題進行簡化，提高了進化算法對該優化問題的求解速度。

然而，Sobol’法局限性在于計算量需求大。根據SALTELLI A等[7]的建議，Sobol’法宜在輸入參數不超過20個且單次模型運行時間小于1 min時使用。當管網模型中有成百上千個參數時，使用Sobol’法分析需耗費大量的計算時間。而GSA中的Morris法能以較小的計算代價獲取參數靈敏度大小的排序以及參數相互作用的定性描述，還鮮有應用于管網模型研究。

針對以上問題，本文提出采用Morris法對管網模型中參數進行全局靈敏度分析，識別關鍵參數，降低問題復雜性。通過紐約隧道管網案例，將Morris法和Sobol’法的靈敏度分析結果進行對比分析，驗證Morris法靈敏度分析的有效性。最后，對管網模型靈敏度分析方法的選擇提出建議。

1 全局靈敏度分析方法

1.1 Morris法

為高效地篩選出模型中的少數重要參數，Morris于1991年提出一種GSA方法[8]。假設模型y(X)有k個參數，對于給定輸入參數X=[x1,x2,…,xk]，第i個參數的一個基本效應為：

EEi=[y(x1,…,xi+△,…,xk)-y(X)]/△

(1)

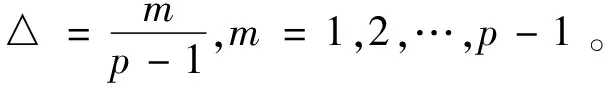
構造m×k(m=k+1)的矩陣B：

(2)

顯然，將B中相鄰兩行作為輸入參數，可計算得到k個基本效應，分別與k個參數對應。矩陣B可稱為參數空間中的一條軌跡。在實際操作中，進行一隨機過程，生成多條軌跡，以充分探索整個參數空間。隨機過程詳見參考文獻[8]。按照預設軌跡數r，計算各參數基本效應的均值μi和標準差σi。μi的值越大，xi對模型輸出的影響越大；而σi的值大，則說明xi對模型輸出的影響是非線性的，或者xi與其他參數存在交互作用，反之亦然。

1.2 Sobol’法

Sobol’法是一種基于方差的全局靈敏度分析方法[9]，能定量評估參數對模型輸出不確定性的貢獻度。其核心是將目標函數的總方差分解成每個參數的方差以及參數之間相互作用的方差。

假設有k個參數的模型目標函數為：

y=f(X)=f(x1,x2,…,xk)

(3)

模型輸出方差D可表示為：

(4)

式中，Di為xi單獨作用造成的輸出方差；Di,j是xi和xj間相互作用的方差；D1,2,…,k為k個參數間相互作用的方差。

將上式左右兩邊同除以D得：

(5)

式中,Si=Di/D，稱為一階靈敏度；Si,j=Di,j/D，稱為二階靈敏度；S1,2,…,k是k階靈敏度。總靈敏度STi=∑S(i)表示xi對模型輸出的總影響，其中S(i)為所有包含參數i的靈敏度。STi-Si可用于表征xi與其他輸入變量之間的交互作用對模型輸出的影響。

通常用Si和STi來評估參數對模型輸出的影響。對于Si和STi的計算，采用Saltelli推薦的方法[10]，需運行模型N(k+2)次。此外，Sobol’方法要求樣本覆蓋整個參數空間，為此采用拉丁超立方抽樣對參數空間進行抽樣。

2 案例分析

以紐約隧道管網為例，展示Morris法和Sobol’法在管網優化設計中的應用，并從計算精度和計算量兩個方面對上述兩個方法進行對比分析。

2.1 紐約隧道問題

紐約隧道問題是由SCHAAKE J C等[11]于1969年提出的，其管網布局如圖1所示，包含1個水源、20個節點和21個管段。為滿足用戶用水需求，需對該管網進行擴建，可在現存的管道旁平行敷設新管。新增管道有16種管徑可選，不同的管徑造價不同。管網多目標優化設計的目的是兼顧經濟性和可靠性，尋求最優解決方案。對于這種優化問題，通常利用進化算法進行求解。但其高維度的參數空間對計算量的需求很大，導致算法搜索效率低下。利用靈敏度分析找出該問題的關鍵參數有助于提高進化算法的搜索效率。

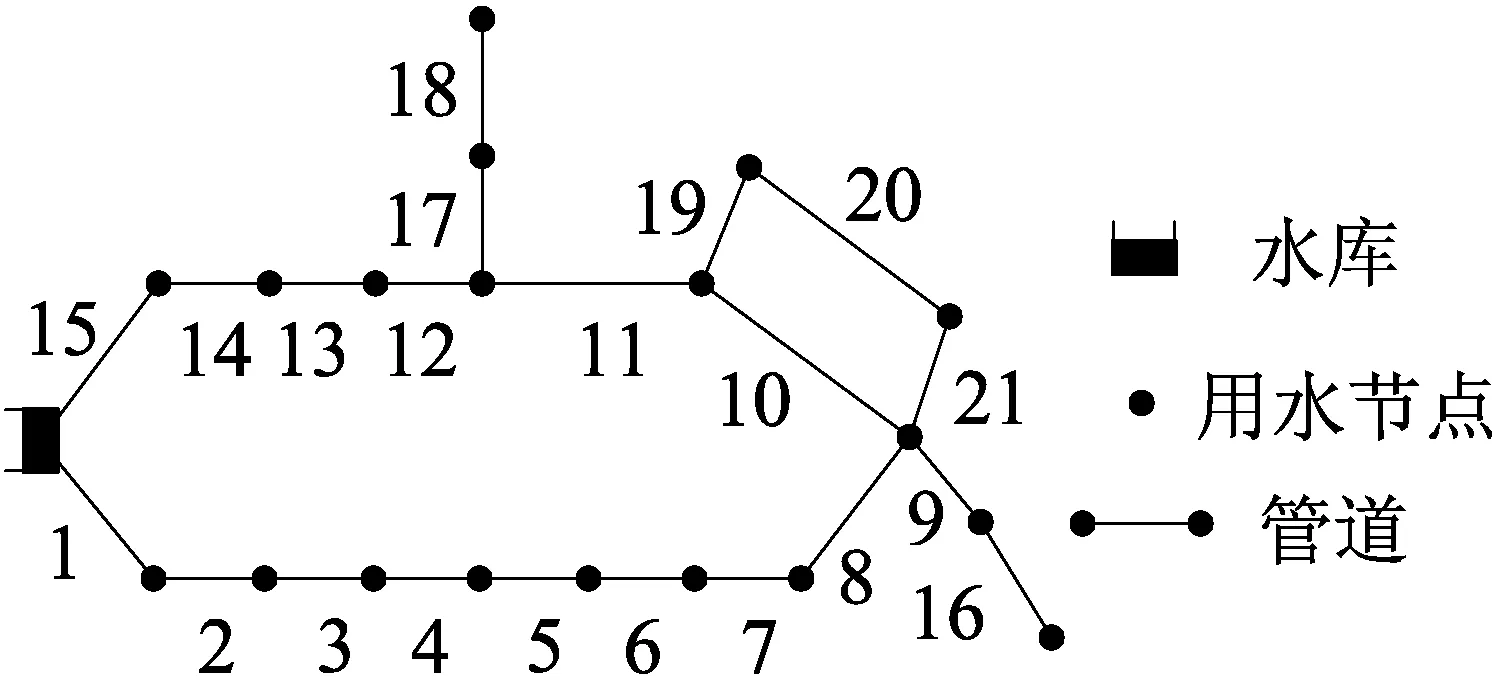
圖1 紐約隧道管網

2.2 目標函數和輸入參數

采用TODINI E[12]提出的一個指標Fresilience來評估管網擴建方案的可靠性，并將該指標作為輸出變量，其計算方法如下：

(6)

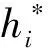
2.3 結果與討論

2.3.1 Sobol’法分析結果

經過多次取樣計算測試穩定性后，取樣本次數為N=2 000，共需運行模型N(k+2)=46 000次。分析結果如圖2所示，各參數一階靈敏度和總靈敏度具體數值見表1。為便于區分，對新增管道進行編號，方法如下：1號新增管道即與1號管道平行敷設的新增管道，依此類推。

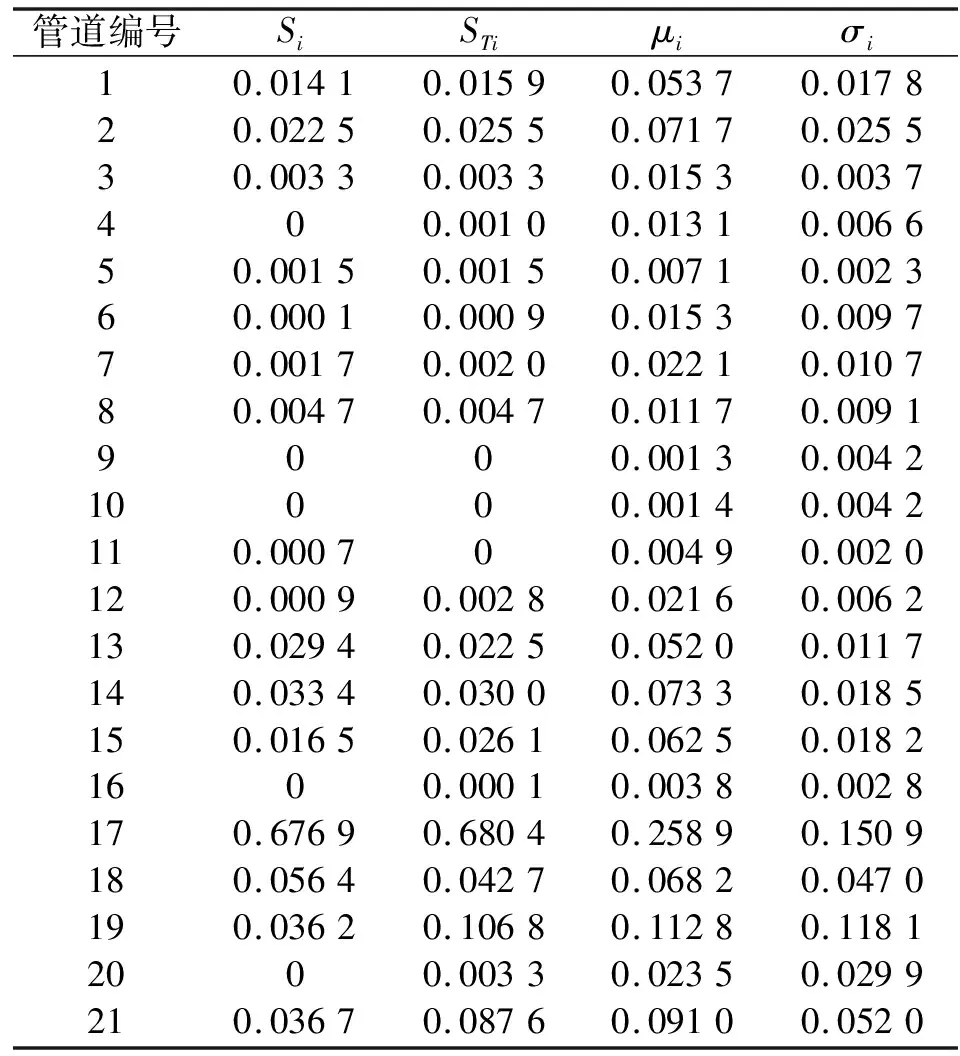
表1 各管道靈敏度值

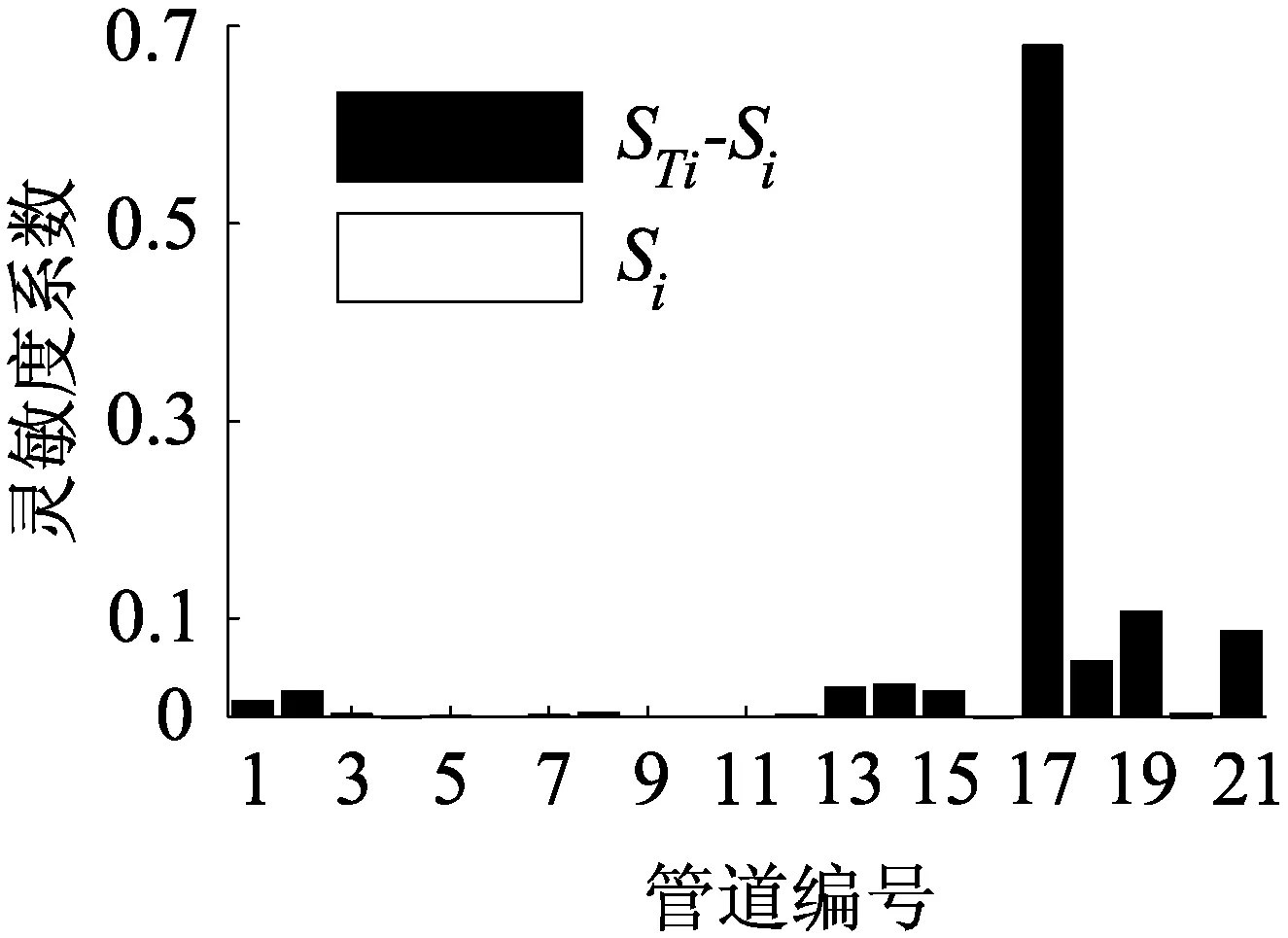
圖2 Sobol’法的分析結果

由圖2可知，目標管網的可靠性受17號新管管徑變化的影響最大，其次為1、2、13、14、15、18、19和21號新增管道，而其余新增管道對管網可靠性的影響非常小，可以忽略；總體上來說，參數間的交互作用對該管網可靠性影響不大。

為驗證Sobol’法分析結果的準確性，設置如下4種情況。Case1：考慮所有新增管道的不確定性，即輸入變量包括所有新增管道；Case2：只考慮1、2、13～15、17～19和21號新增管道的不確定性，其余新增管道管徑取值為8 in(可選管徑的中間值)；Case3：只考慮17號新增管道的不確定性，其余新增管道管徑取值為8 in；Case4：考慮3～12、16和20號新增管道的不確定性，其余新增管道管徑取值為8 in。通過蒙特卡洛模擬對以上4種情況進行不確定性分析，對每種情況均隨機取樣2 000次，計算后得到紐約隧道管網可靠性的經驗累積分布函數(CDF)曲線如圖3所示。

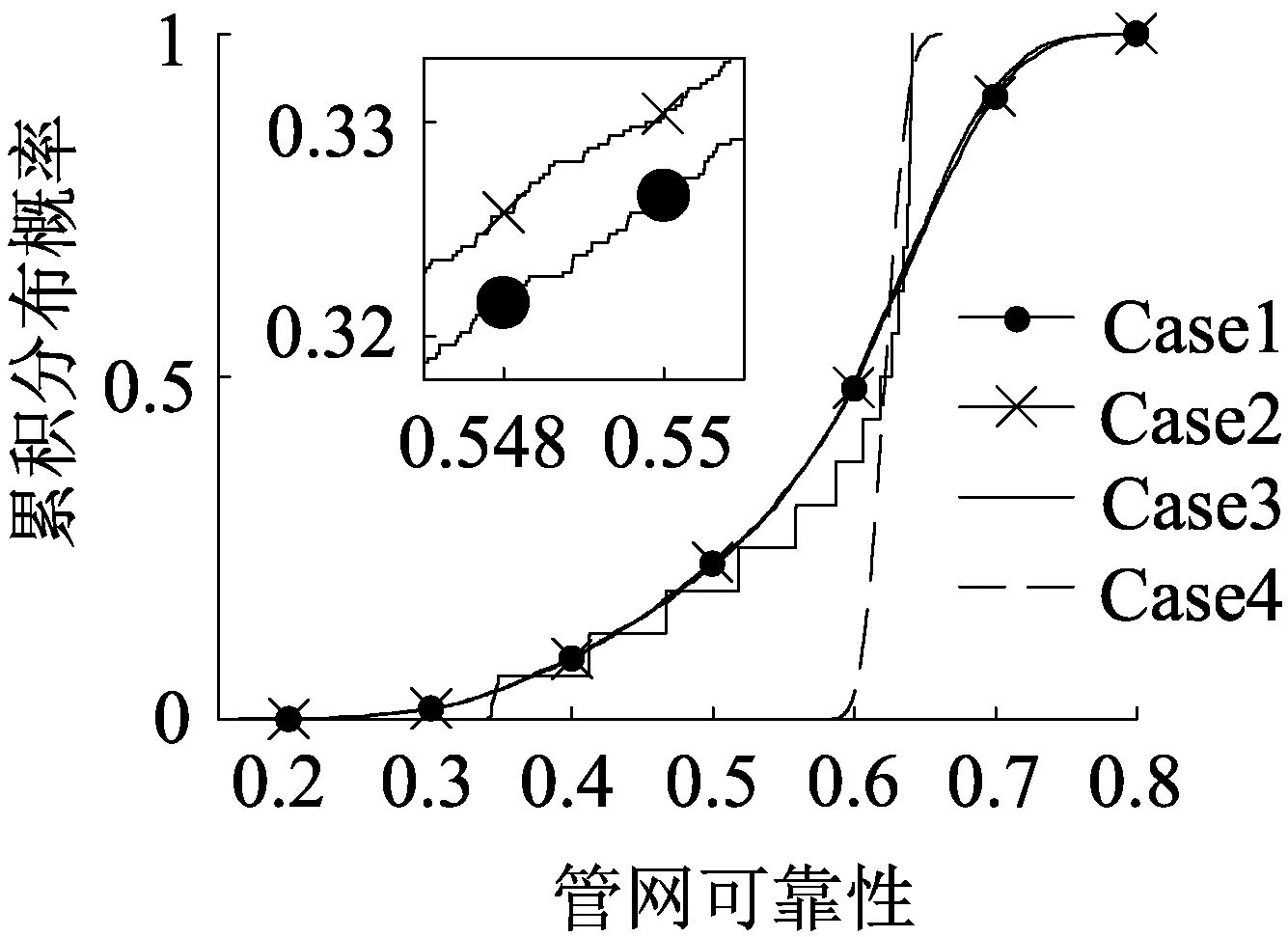
圖3 4種情況的累積分布曲線

由圖3可知，當僅考慮最重要參數的不確定性(Case3)時，其CDF曲線與考慮所有參數不確定性(Case1)的CDF曲線相比，趨勢大致相同；當只考慮重要參數的不確定性(Case2)時，CDF曲線與考慮所有參數不確定性(Case1)的CDF曲線基本一致；而僅考慮不重要參數(Case4)時，其CDF曲線接近于直線，管網可靠性的變化非常小。因此，由Sobol’法分析得到的參數靈敏度是可靠的。

根據總靈敏度對重要管道進行排序，Sobol’法分析得到的管道排序依次為17、19、21、18、14、15、2、13和1。

2.3.2 Morris法分析結果

Morris法參數設置：p=4，r=10。共運行模型r(k+1)=220次，Morris法分析結果如圖4所示，各管道靈敏度具體數值如表1所示。由圖表可知，3～12、16和20號新增管道的μi和σi值都很小，表明其對管網可靠性的影響很小, 是不重要參數；其余新增管道的μi值和σi值相對較大，表明它們對管網可靠性的影響較大，且其效應的非線性程度較高或與其他參數間存在交互作用，是重要參數。根據μi值對重要管道進行排序，Morris法分析得到的管道排序依次為17、19、21、18、14、15、2、1和13。

圖4 Morris法的分析結果

2.3.3 Morris法與Sobol’法的對比分析

對3～12、16和20號新增管道，Morris法和Sobol’法的分析結果一致，是不重要參數；對于其余重要參數，Morris法分析得到的參數靈敏度排序與Sobol’法所得排序大致相同，但Morris法不能對參數間的交互作用進行詳細分析。值得注意的是，雖然Morris法的精度稍差于定量分析的Sobol’法，但其所需樣本量遠小于后者。也就是說，相對于Sobol’法，Morris法能以較小的計算代價識別重要參數，并獲得比較準確的參數靈敏度排序。

3 結論與建議

根據已有研究表明：在基于供水管網模型的分析和設計中，輸出結果的不確定性主要受少數重要參數的影響。為提高識別模型中重要參數的效率，本文提出采用Morris法進行全局靈敏度分析。通過紐約隧道案例，從計算效率、計算精度方面對Morris法和Sobol’法進行詳細對比，結果表明：Sobol’法雖然能定量評估輸入參數對模型輸出的影響，但所需計算量大；Morris法精度稍差，但能以較小的計算代價獲得參數靈敏度的定性描述，其計算量遠小于Sobol’法。

根據管網模型復雜程度和使用目的，對全局靈敏度分析方法的選擇提出以下建議：

(1)當管網模型參數較少時(不多于20個)，若需要對各參數的作用進行詳細分析，可選擇Sobol’法；若只需大致的參數靈敏度排序，可選擇Morris法進行分析。

(2)當管網模型輸入參數眾多時，可考慮先采用Morris法篩選出模型的重要參數，再采用Sobol’法定量分析重要參數對模型輸出的影響，以降低計算時耗。