基于優化灰色模型的南海鳶烏賊資源豐度預測

周茜涵，吳洽兒，周艷波，謝恩閣，馬勝偉

（1.中國水產科學研究院南海水產研究所/農業農村部南海漁業資源開發利用重點實驗室，廣東 廣州 510300；2.西安電子科技大學數學與統計學院，陜西 西安 710100）

鳶烏賊 (Sthenoteuthis oualaniensis) 隸屬于槍形目、柔魚科、鳶烏賊屬，廣泛分布于印度洋、太平洋的赤道和亞熱帶海域，其中南海和印度洋西北部海域分布數量較多。巨大的開發潛力與經濟價值，使其在我國南海海洋漁業中的地位日益凸顯，近年已逐漸成為我國南海重要經濟種之一[1]。海洋環境和氣候均會對南海鳶烏賊的相對資源豐度產生影響，如海表面溫度 (Sea surface temperature, SST)、海平面高度 (Sea surface height, SSH)、海表葉綠素a濃度 (Sea surface chlorophyllaconcentration, Chla)、海表鹽度 (Sea surface salinity, SSS)、厄爾尼諾現象[2]、月相等[3]，掌握南海鳶烏賊單位捕撈努力量漁獲量 (Catch per unit effort, CPUE) 與海洋環境間的變化規律，對準確預測鳶烏賊的資源豐度有重大意義。但由于鳶烏賊資源開發較晚，漁獲量統計數據缺少長時間與大范圍的積累，且漁民自主填報數據質量較差，傳統方法難以對其資源豐度進行準確預測[4]。灰色系統模型由我國鄧聚龍教授首創，旨在解決“部分信息已知，部分信息未知”的不確定性系統問題，對時間序列較短的數據和具有不確定因素的復雜系統的預測效果較好[5]，近年來已被廣泛應用于漁業研究領域[6]。普通GM (1,1) 模型每次僅能觀測1個變量，無法體現環境因子的作用；GM (1,N) 模型雖能考慮多個變量的影響作用，體現出多因素共同作用下的趨勢預測，但建模精度存在較大偏差，穩定性不足[7]。針對上述問題，許多學者對灰色模型進行了優化改進，如構建無偏模型[8]、優化灰作用量[9]、重構背景值[10]、優化參數估計[11]以及殘差序列修正[12]等。本文以2013—2019年春夏季南海鳶烏賊CPUE為資源相對豐度指標，構建鳶烏賊CPUE與環境因子間的灰色預測模型GM (1,N)[13]，并對原始預測模型進行優化，以提高預測精度。

1 材料與方法

1.1 數據來源

南海鳶烏賊生產統計資料來自于廣西壯族自治區北海市水產推廣站漁撈日志，數據包括船名、主機功率、日期、作業水深、經度、緯度、漁區、作業時長、漁獲量 (kg) 等，因本文選取的漁船參數變化較小，故暫未考慮漁船參數對CPUE的影響[14]。時間分辨率為天 (d)，空間分辨率為經緯度0.5°×0.5°。研究區域為 106°E—120°E、6°N—20°N，時間為2013—2019年。根據鳶烏賊的汛期，本文以每年2—6月汛期為研究對象[15]。

本研究選取SST、SSH、Chl-a、SSS和海表面風速 (Sea surface wind, SSW) 5種與鳶烏賊活動密切相關的環境因子[16]，其中SST、SSS、Chl-a和SSW數據來源于美國海洋大氣局NOAA氣候觀測網點https://oceandata.sci.gsfc.nasa.gov/，時間分辨率均為月，SSS和SSW的空間分辨率為0.25°×0.25°，SST和Chl-a的空間分辨率為4 km。SSH數據來源于http://marine.copernicus.eu，時間分辨率為月，空間分辨率為0.083°×0.083°。在ArcGis 10.2中將空間分辨率統一處理為0.5°×0.5°，若存在未記錄的環境數據，則采用克里格插值計算得到相應站點的環境數據[17]。

1.2 研究方法

1.2.1 數據預處理 本研究以CPUE作為鳶烏賊資源相對豐度的指標，計算歷年各月平均CPUE，計算公式為：

1.2.2 灰色關聯分析 灰色關聯分析是根據灰色系統中各因素間發展趨勢來確定各因素間關聯性，對系統的變化趨勢作量化度量[19]。本文設序列為2013—2019年各年平均CPUE序列，設序列為歷年各月環境因子序列，之間的關聯度計算參考余勝威[20]。

各指標對CPUE的影響程度大小與關聯度成正比，關聯度越大說明影響越大，反之越小。通常關聯度大于0.9說明兩者之間具有強相關，大于0.8說明兩者之間顯著相關，大于0.7說明具有相關性[20]。

1.2.3 GM (1,N) 模型預測原理 GM (1,N) 模型是多變量情況下考慮觀測點間相關性的動態關聯分析模型，能反映系統參數間的影響作用，適用于系統整體分析。設各年平均CPUE序列為，其相關海洋環境因素序列為模型的具體構建計算參考文獻[21]。

最終得到G M (1,N) 的響應函數為：

累減還原預測值：

1.2.4 因子重要性分析 因子重要性分析是通過關聯度分析和因子組合共同確定因子重要性的方法，即為比較不同環境因子對資源相對豐度預測的效果，模型建立時考慮不同因子的組合模型，擬構建以下6種模型[13]：

模型1：包含所有因子的GM (1,6) 模型；

模型2：不包含SSH的GM (1,5) 模型；

模型3：不包含SST的GM (1,5) 模型；

模型4：不包含SSS的GM (1,5) 模型；

模型5：不包含Chl-a的GM (1,5) 模型；

模型6：不包含SSW的GM (1,5) 模型。

通過相對誤差判斷模型有效性，即比較以上所有模型的相對誤差大小來間接說明該環境因子的重要性[22]。

1.2.5 基于Simpson公式的背景值優化 GM(1,N) 模型的預測值依賴于原始數據序列及其背景值，因此背景值的合理構造將對提高模型預測精度起重要作用。通常使用的兩點間中值誤差較大，且會造成預測值數據不夠平穩，故此選用Simpson公式對背景值進行改造[21]。

新的背景值寫作[23]：

1.2.6 基于Fourier級數的殘差修正 灰色GM(1,N) 模型在進行中長期預測時預測精度會衰減，針對這個問題，可以基于構建殘差的GM (1,1) 模型[24]、Markov鏈[25]、自適應濾波法[26]等方法修正。本文采用Fourier級數對預測誤差做擬合修正。定義灰色GM (1,N) 模型的殘差序列為：

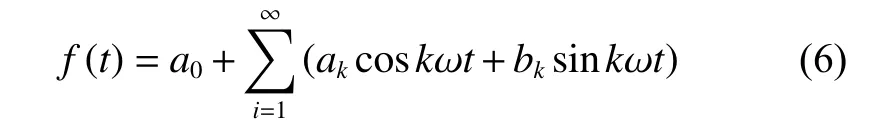
其中模型相應參數可通過Matlab 2017a軟件求解[27]。

2 結果

2.1 CPUE年際變化規律

南海鳶烏賊年CPUE存在較大的變動，2013—2015年逐年增加，在2015年達到最高值(2.66 t·d?1)后下降至 2016 年的 1.93 t·d?1，隨后在 2017—2019年間呈穩步增長的趨勢 (圖1)。

圖1 2013—2019年南海鳶烏賊單位捕撈努力量漁獲量變化Figure 1 CPUE of S.oualaniensis in South China Sea from 2013 to 2019

2.2 灰色關聯分析

環境因子中Chl-a、SST和SSW的關聯度皆大于0.8，屬于顯著相關；SSS和SSH的關聯度大于0.7，具有相關性 (表1)。其中影響最大的因子是Chl-a，其灰色關聯度平均值為0.953 5；其次為SST，平均關聯度為0.848 0；第三為SSW，平均關聯度為0.833 8。

表1 環境因子序列與單位捕撈努力量漁獲量的灰色關聯度分析結果Table 1 Grey relational analysis of environmental factor sequence and CPUE

從月份因素分析，3月的Chl-a和SSW、2月的SST、5月的SSH和SSS分別為各因子中關聯系數最大的月份，因此在之后GM (1,N) 模型構建中，采用上述5項因子作為南海鳶烏賊資源GM(1,N) 模型建模的備選因子。

GAM模型分析表明 (圖2)，鳶烏賊CPUE集中分布在 Chl-a質量濃度介于 0.07～0.19 mg·m?3的區域，最適宜 Chl-a質量濃度為 0.09～0.13 mg·m?3；鳶烏賊CPUE集中分布的SST介于24～31 ℃，最適宜SST為27～29 ℃；鳶烏賊CPUE集中分布的SSW介于 2.0～10.0 m·s?1，最適宜風速為 4.5～7.0 m·s?1。

圖2 海表面葉綠素質量濃度、海表面溫度和海表面風速對單位捕撈努力量漁獲量的影響Figure 2 Effects of sea surface Chl-a concentration, sea surface temperature, sea surface wind speed on CPUE

2.3 灰色預測模型

選定指標后，用2013—2018年CPUE和環境因子數據建立灰色預測模型，多種因子組合模型的平均相對誤差見表2。從平均相對誤差上看，模型M6 (不包含SSS) 和模型M3 (不包含SSW) 相對誤差值較大，模型M1 (包含全部因子) 相對誤差最小，即模型M1為最優預測模型，能夠較好地模擬南海春、夏季鳶烏賊的資源豐度。

表2 多因素預測模型得到的單位捕撈努力量漁獲量擬合值與真實值的相對誤差Table 2 Relative error between CPUE predictive value and real value obtained by multi-factor prediction model

2.4 優化的 GM (1,N) 模型

表3為CPUE真實值與普通GM (1,6) 模型、基于Simpson優化的GM (1,6) 模型和基于Fourier級數修正的GM (1,6) 模型3種模型擬合結果的比較。因數據列較短，在此只選用2019年的數據作驗證。

表3 3種模型的擬合結果與單位捕撈努力量漁獲量真實值的相對誤差Table 3 Relative error between predictive values of three models and real CPUE value

普通GM (1,6) 模型平均相對誤差為7.78%，預測的2019年CPUE誤差為4.79%。

根據公式 (4) 計算基于Simpson公式的GM(1,N) 模型，平均相對誤差為7.69%，預測的2019年CPUE誤差為3.46%。

根據公式 (6) 使用2013—2018年殘差擬合Fourier級數得到級數表達式為：

模型殘差平方和SSE=0.025，擬合優度值R2=0.879，均方根誤差RMSE=0.158 2，此時基于Fourier級數修正的GM (1,N) 模型的平均相對誤差僅為2.62%，預測的2019年CPUE相對誤差僅為1.87%。

普通GM (1,6) 模型的結果不平穩，在2014和2017年的擬合上出現了較大的誤差；基于Simpson優化的GM (1,N) 模型預測數據平穩但仍有誤差；而基于Fourier級數殘差修正的灰色GM (1,N) 模型基本能擬合真實值 (圖3)。

圖3 3種模型的擬合結果與單位捕撈努力量漁獲量真實值的比較Figure 3 Comparison between fitting results of three models and real CPUE value

3 討論

本研究以CPUE為指標，結合海洋環境因子，采用灰色系統理論預測春夏季南海鳶烏賊的資源豐度，并用數值積分中的Simpson公式和Fourier級數對模型的背景值和殘差進行修正，得到較普通灰色模型精確度更高的預測方法。

3.1 環境因子對CPUE的影響

灰色關聯度結果表明，Chl-a對鳶烏賊CPUE的影響最大，其灰色關聯度平均值為0.953 5。在漁場的變化中，Chl-a濃度決定了海域生產力高低以及攝食環境優劣，而攝食環境是決定鳶烏賊補充量的重要因素[13]。本研究結果顯示，鳶烏賊集中分布在 Chl-a質量濃度介于 0.07～0.19 mg·m?3的區域，最適宜 Chl-a質量濃度為 0.09～0.13 mg·m?3。這與余景等[16]報道的中西沙鳶烏賊最適Chl-a質量濃度為 0.10～0.13 mg·m?3的結果一致。

鳶烏賊的生存環境與溫度密切相關[14]。徐紅云等[28]報道南海鳶烏賊中心漁場最適宜SST為26.4～29.6 ℃；晏磊等[29]研究認為不同季節鳶烏賊對溫度的適宜性范圍也有所變化，春季最適SST為25.6～29.6 ℃，秋季為27.6～30 ℃。本研究中SST對CPUE的影響僅次于Chl-a，關聯度為0.848，主要分布在27～29 ℃，與上述研究結果基本一致。

SSW的平均關聯度為0.833 8。本研究中鳶烏賊 CPUE分布在 SSW 介于 2.0～10.0 m·s?1的區域，其中最適宜SSW為4.5～7.0 m·s?1。風速對鳶烏賊CPUE的影響與燈光罩網作業的特點有關，大風天氣會嚴重影響罩網漁船捕撈作業，在海上風速較大時其捕撈活動較少。

此外，有研究表明，SSH也是影響鳶烏賊資源豐度的一個重要因子，SSH高于平均海面有利于海水的輻散上升，帶來豐富的營養物質，使浮游生物大量繁殖，充足的餌料可促進中上層魚類的生長、繁殖[30]。但本研究將整個海域SSH進行了平均，且研究時間僅2—6月，弱化了SSH對CPUE的影響[13]。

3.2 優化灰色模型的作用

灰色GM (1,N) 模型結果顯示，包含所有因子的模型M1對鳶烏賊資源豐度有較好的預測效果，能較準確地反映CPUE的變化趨勢。灰色系統模型突破小樣本數據的局限，對時間序列較短的數據也有良好的預測效果，對數據缺乏的漁業科學具有重要意義。

針對普通灰色模型預測誤差較大的問題，本文首先使用Newton-Cotes公式改造背景值，用Simpson公式代替梯形公式，降低背景值帶來的誤差。將GM (1,N) 模型的平均相對誤差由7.78%降至7.69%，使預測數據序列更平穩；且與普通GM(1,N) 模型相比，使2019年CPUE的預測誤差從4.79%降至3.46%，因此改造背景值對于優化預測結果有一定意義。此外，用Fourier級數對GM(1,N) 模型的殘差作擬合，利用其良好的數據逼近能力對預測誤差進行修正，將數據序列的平均相對誤差由7.78%降至2.54%，將2019年CPUE的預測誤差從4.79%降至1.87%，說明Fourier級數修正能夠有效地提高模型精度，減少相對誤差，使結論更具實際價值。

綜上所述，本研究通過灰色關聯分析法構建鳶烏賊CPUE與環境因子間的關聯度，選取合適因子構建灰色預測模型對南海鳶烏賊資源CPUE進行預測，并對其結果進行修正，使優化后的模型較之前的精度有明顯提高，這對更準確預測鳶烏賊資源豐度提出了一種新思路。但本文未考慮因子交互項對南海鳶烏賊CPUE的作用，加上灰色系統模型本身的局限性，如快速衰減和遞增的屬性，使長期預測結果的準確性較低。本研究因GM (1,N) 模型對加入的影響因素的限制，在計算CPUE時采取了平均的算法，降低了樣本量。因此，今后可嘗試其他預測模型，如神經網絡模型[31]和回歸樹模型[32]，兩者均具有良好的非線性映射能力和學習能力，在大樣本量條件下能獲得更高的預測結果；此外，支持向量機模型[33]能根據有限的樣本信息在模型的復雜性和學習性之間尋求最佳解，在小樣本情況下得出較好的預測結果，從而獲得更加準確的南海鳶烏賊CPUE預測模型。