Symmetry Classification of Partial Differential Equations Based on Wu’s Method
TIAN Yi (田 毅), WAN Jianxiong (萬劍雄)
1 College of Data Science and Application, Inner Mongolia University of Technology, Hohhot 010080, China
2 Inner Mongolia Autonomous Region Engineering & Technology Research Center of Big Data Based Software Service, Hohhot 010080, China
Abstract: Lie algorithm combined with differential form Wu’s method is used to complete the symmetry classification of partial differential equations(PDEs) containing arbitrary parameter. This process can be reduced to solve a large system of determining equations, which seems rather difficult to solve, then the differential form Wu’s method is used to decompose the determining equations into a series of equations, which are easy to solve. To illustrate the usefulness of this method, we apply it to some test problems, and the results show the performance of the present work.
Key words: Lie algorithm; differential form Wu’s method; determining equation; symmetry classification; partial differential equation(PDE)
Introduction
In the past decades, a wealth of methods have been developed to deal with exact solutions of partial differential equations (PDEs). Some of the most important methods are the homotopy perturbation method[1-3], variational iteration method[4-6], Taylor series method[7]and variable separation method[8-9], a new direct method[10],etc. The exp-function method[11-13]is used to obtain generalized solitonary solutions and periodic solutions for nonlinear evolution equations arising in mathematical physics using symbolic computation, the method is straightforward and concise, and its applications are promising. The semi-inverse variational method[14]is systematically studied and many examples are given to show how to establish a variational formulation for a nonlinear equation. At present, symmetries of PDEs are widely used in mechanics, mathematics and physics fields, from symmetries of PDEs, one can obtain more important information on solving PDEs, such as exact solutions, conservation laws and integral factors. Hence the topics finding symmetries of PDEs have being brought the interest of more and more people. We have done some work on symmetries of PDEs. In Ref. [15] the Wu’s method is used to complete symmetry classification of PDEs, the approach is not the same as the Wu’s method used in this paper. In Ref. [16] the traditional Lie algorithm is used to complete symmetry classification of the diffusion-convection equation. In Ref. [17] the Wu’s method is used to simplify the symmetry computation of PDEs and a special symmetry reduction approach is used for a class of wave equations.
In symmetry analysis of PDEs, the problems of determining symmetry can be come down to solving over-determined PDEs (determining equations). However the over-determined PDEs are usually large and not easy to solve directly. For a well understanding, in the next, we briefly review the symmetry computation problem of PDEs[16-17]. In this paper, differential form Wu’s method is used to decompose the determining equations into a series of equations, which are easy to be solved. This is also an application of Wu’s method in the field of differential equations.
1 Lie Algorithm
Consider the following PDE
F(x,u, ?u, ?2u, …, ?ku)=0,
(1)
wherex=(x1,x2, …,xn) denotes the coordinates corresponding to itsnindependent variables,udenotes the coordinate corresponding to its dependent variables, and ?judenotes the coordinates with components ?ju/(?xi1?xi2…?xij)=ui1i2…ij,ij=1,2, …,nforj=1,2, …,k, corresponding to alljth-order partial derivatives ofuwith respect tox.
Definition1The one-parameter Lie group of point transformations
(2)
leaves invariants Eq. (1),i.e., Eq. (2) is a point symmetry admitted by Eq. (1), if and only if itskth extension leaves invariant the surface Eq. (1).
Theorem1Let
(3)
be the infinitesimal generator of Lie group of point transformations of Eq. (2). Let
(4)
be thekth-extended infinitesimal generator of Eq. (3). Then one-parameter Lie group of point transformations Eq. (2) is admitted by Eq. (1),i.e., Eq. (2) is a point symmetry admitted by Eq. (1), if and only if
X(k)F(x,u, ?u, ?2u, …, ?ku)=0,
(5)
whenF(x,u, ?u, ?2u, …, ?ku)=0.
2 Differential Form Wu’s Method
Suppose determining equations (DTEs) and nonzero coherent differential polynomial (IP) are differential polynomials system (DPS), introduce the following notations:
Tzero(DTEs)= all solutions ofDTEs=0;
Tzero(DTEs/IP)= all solutions ofDTEs=0, such thatIP≠0;
Tzero(DTEs,IP)= all solutions ofDTEs=0, such thatIP=0;
Premd(DTEs/DCS)= the set of pseudo-remainders ofDTEswith respect to chainDCS.
ISdenotes the initials and separants products for differential polynomials calledISproducts.
In the following, we list the basic results of differential form Wu’s method[15,18-19].
Definition2A lowest rank differential chain contained in a dps is called a basic set of the DPS.
Theorem2LetDPSbe a finite DPS, there is an algorithm (Wu’s method) which permits one to determine a differential chainDCS, called characteristic set of systemDPS, such that
Tzero(DCS/IS)?Tzero(DPS)?Tzero(DCS),
Premd(DPS/DCS)=0,
Tzero(DPS)=Tzero(DCS/IS)∪Tzero(DPS,IS),
whereISis a product of initials and separants of the characteristic setDCS.
Theorem3For a given finite DPSDPS, Wu’s algorithmic yield finite differential characteristic setDCSkofDPSwith initials and separants productsISksuch that the following zero decomposition
is held.
The algorithm to determine characteristic setDCSis listed as follows.
InputA DPSDPS.
OutputA differential characteristic setDCS.
StartLeti=0.
Step1Select a basic setDBSifromDPSi.
Step2Compute all the nonzero coherent DPS ofDBSi, and put them in setT′i.
Step3?IP(nonzero coherent differential polynomial) ∈T′i, computePremd(IP/DBSi){0}, and put the results in set T i.
Step4Compute Ri=Premd((DPSiDBSi)/DBSi){0}, and let J i=T i∪R i.
Step5 IfJi=?(empty set), thenDCS=DBSi, and stop, elsei=i+1 andDPSi=DPSi-1∪Ji-1, go to step 1.
3 Results and Discussion
In this section, we perform tests for the algorithm described in previous sections.
Example1Consider the following equation
ut+f′(u)ux+uxxx=0,
(6)
and suppose that the infinitesimal generator admitted by Eq. (6) is
From Eq. (5), the determining equations forXare
Taking left hand of each equation inDTE,we have
Step1ComputeTzero(DPS).
Under the rankx DCS1={ξu,ξt,ξx,ηu,ηt,ηx,τ} withISproductsI1·I2≠0, and I1=f(3)(u)2f(4)(u)-2f″(u)f(4)(u)2+f″(u)f(3)(u)f(5)(u), I2=6f(3)(u)3f(4)(u)2-12f″(u)f(3)(u)f(4)(u)3- 4f(3)(u)4f(5)(u)+12f″(u)f(3)(u)2f(4)(u)f(5)(u)+f″(u)2f(4)(u)2f(5)(u)-2f″(u)2f(3)(u)f(5)(u)2-2f″(u)f(3)(u)3f(6)(u)+f″(u)2f(3)(u)f(4)(u)f(6)(u). Then, we get Tzero(DPS)=Tzero(DCS1/I1·I2)+Tzero(DPS,I1)+Tzero(DPS,I2), in which Tzero(DCS1/I1·I2)={ξ=c1,η=c2,τ=0}, andc1,c2are arbitrary constants. Step2I1=0, computeTzero(DPS,I1). Obtain the characteristic set withISproductsI3≠0, and I3=-2f(3)(u)2+f″(u)f(4)(u). Then, we getTzero(DPS,I1)=Tzero((DCS2,I1)/I3)+Tzero(DPS,I1,I3), in which with the corresponding function Step3I3=0, computeTzero(DPS,I1,I3). Obtain the characteristic set withISproductsI4≠0, and I4=f(3)(u). Then, we get Tzero(DPS,I1,I3)=Tzero((DCS3,I1,I3)/I4)+Tzero(DPS,I1,I3,I4), in which with the corresponding function Step4I4=0, computeTzero(DPS,I1,I3,I4). Obtain the characteristic set withISproductsI5≠0, and I5=f″(u), Then, we get Tzero(DPS,I1,I3,I4)=Tzero((DCS4,I1,I3,I4)/I5)+Tzero(DPS,I1,I3,I4,I5), in which Step5I5=0, computeTzero(DPS,I1,I3,I4,I5). Obtain the characteristic set withISproducts ? (empty set). Then, we get Tzero(DPS,I1,I3,I4,I5)=Tzero(DCS5,I1,I3,I4,I5), in which and and with the corresponding functionf(u)=c1u+c2, andc1,c2,c3are arbitrary constants. Step6ComputeTzero(DPS,I2) Obtain the characteristic setDCS1withISproductsI6≠0, and I6=f(3)(u)2f(4)(u)-2f″(u)f(4)(u)2+f″(u)f(3)(u)f(5)(u). Then, we get Tzero(DPS,I2)=Tzero((DCS1,I2)/I6)+Tzero(DPS,I2,I6), in which Tzero((DCS1,I2)/I6)=Tzero(DCS1/I1·I2). Step7I6=0, computeTzero(DPS,I2,I6). Obtain the characteristic setDCS2withISproductsI3≠0.Then, we get Tzero(DPS,I2,I6)=Tzero((DCS2,I2,I6)/I3)+Tzero(DPS,I2,I6,I3), in which Tzero((DCS2,I2,I6)/I3)=Tzero((DCS2,I1)/I3). Step8I3=0, computeTzero(DPS,I2,I6,I3). Obtain the characteristic setDCS3withISproductsI4≠0.Then, we get Tzero(DPS,I2,I6,I3)=Tzero((DCS3,I2,I6,I3)/I4)+Tzero(DPS,I2,I6,I3,I4), in which Tzero((DCS3,I2,I6,I3)/I4)=Tzero((DCS3,I1,I3)/I4). Step9I4=0, computeTzero(DPS,I2,I6,I3,I4). Obtain the characteristic setDCS4withISproductsI5≠0.Then, we get Tzero(DPS,I2,I6,I3,I4)=Tzero((DCS4,I2,I6,I3,I4)/I5)+Tzero(DPS,I2,I6,I3,I4,I5), in which Tzero((DCS4,I2,I6,I3,I4)/I5)=Tzero((DCS4,I1,I3,I4)/I5). Step10I5=0, computeTzero(DPS,I2,I6,I3,I4,I5). Obtain the characteristic setDCS5withISproducts ? (empty set). Then, we get Tzero(DPS,I2,I6,I3,I4,I5)=Tzero(DCS5,I2,I6,I3,I4,I5), in which Tzero(DCS5,I2,I6,I3,I4,I5)=Tzero(DCS5,I1,I3,I4,I5). ConsideringSteps1-10, we have Tzero(DPS)=Tzero(DCS1/I1·I2)+Tzero((DCS2,I1)/I3)+Tzero((DCS3,I1,I3)/I4)+Tzero((DCS4,I1,I3,I4)/I5)+Tzero(DCS5,I1,I3,I4,I5). Example2Consider the following equation (7) Suppose that the infinitesimal generator admitted by Eq. (7) is From Eq. (5), the determining equations forXare Under the rankx f′(u)f″(u)f(4)(u). Then, we get in which andc1,c2,c3are arbitrary constants. Obtain the characteristic set Then, we get in which with the corresponding function Obtain the characteristic set Then, we get in which Obtain the characteristic set withISproducts ? (empty set). Then, we get in which and with the corresponding functionf(u)=c1u+c2, andc1,c2, …,c6are arbitrary constants. ConsideringStep1toStep4, we have In this paper, we use Lie algorithm to determine the symmetry of given PDEs with parameters. Firstly, we obtain over-determined PDEs (determining equations), which are rather difficult to solve. Then the differential form Wu’s method is used to decompose the determining equations into a series of equations (characteristic set), which are easy to solve. Examples show that this method is effective to compute the symmetry of PDEs and applicable to nonlinear PDEs in different cases.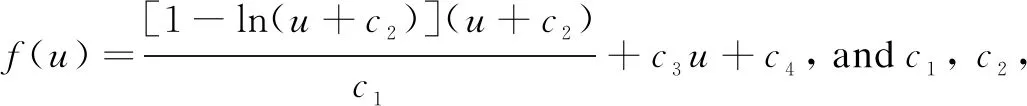
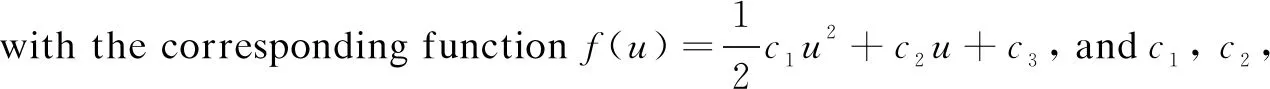

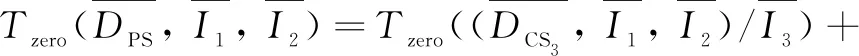
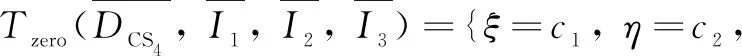
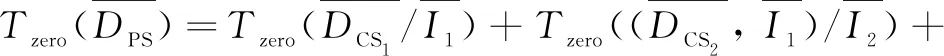
4 Conclusions
 Journal of Donghua University(English Edition)2021年2期
Journal of Donghua University(English Edition)2021年2期
