均勻帶電半球面軸線上場強的計算*
白春華 高國明 文麗敏
(云南大學地球科學學院 云南 昆明 650500)
1 均勻帶電球面和半球面電場強度的相關計算
電磁學教學中電場強度的計算是一個重要且基礎的問題.有關電場強度的計算可以總結歸納出幾種常用方法[1,2]:(1)場強疊加原理;(2)高斯定理;(3)電場和電勢的梯度關系.上述各種方法中,場強疊加原理是求解電場強度最基本的方法,適用于求解各種電荷分布的帶電體的場強分布;高斯定理在求解電荷分布具有高度對稱性(球對稱、軸對稱、平面對稱)的幾何體的電場時非常簡便.除此之外,還可以利用電勢和電場強度的梯度關系先求電勢再求電場分布.近年來,學者們對均勻帶電球面電場的求法以及能否求解球面上的電場進行了反復分析和討論[3~6].由于不能把高斯面取在帶電表面上,所以面上的場強不能由高斯定理直接求出.雖然均勻帶電幾何面兩側的場強會發生躍變,但面上的電場強度也有唯一的確定值.
我們在教學中發現,當遇到所求問題為均勻帶電球面、圓柱面、多層同心球面、同軸柱面等,學生利用高斯定理很容易就能求解出空間電場的分布,但對半球面電場該如何求解并不是很清楚.因為半球面上的電荷分布沒有整個球面那樣高度的球對稱性,所以我們不能利用高斯定理求解.一般而言,適用球面電場的計算方法大多適用于計算半球面的電場.張曉燕等根據疊加原理求解了均勻帶電半球面底面上的電勢分布和電場強度[7].何海衛等分析了均勻帶電半球殼軸線上的電場及其增減性[8].林建福先利用積分法求出均勻帶電半球面軸線上的電勢表達式,然后利用電場強度與電勢的關系導出均勻帶電半球面軸線上的電場強度[9].王世芳等利用圓環帶法、電勢梯度法等多種方法求解均勻半球面球心處的電場強度[10].
上述研究利用多種解法給出了均勻帶電半球面的電場強度.作為一種補充,下面我們直接利用庫侖定律和場強疊加原理,通過球面積分的方法計算均勻帶電半球面在球心、球面上以及球面內外的電場分布,并給出電場分布的E-z曲線.
2 用場強疊加原理計算均勻帶電半球面軸線上的電場強度
【例題】設均勻帶電半球面電荷面密度為σ,半徑為R,求半球面軸線上電場強度的分布.
2.1 均勻帶電半球面在球心處的電場強度
取如圖1所示的xyz坐標系,半球面位于z軸正半軸.場點P點為半球面軸線上一點,當P點取在球心O處時,在半球面上任取一面積元dS.
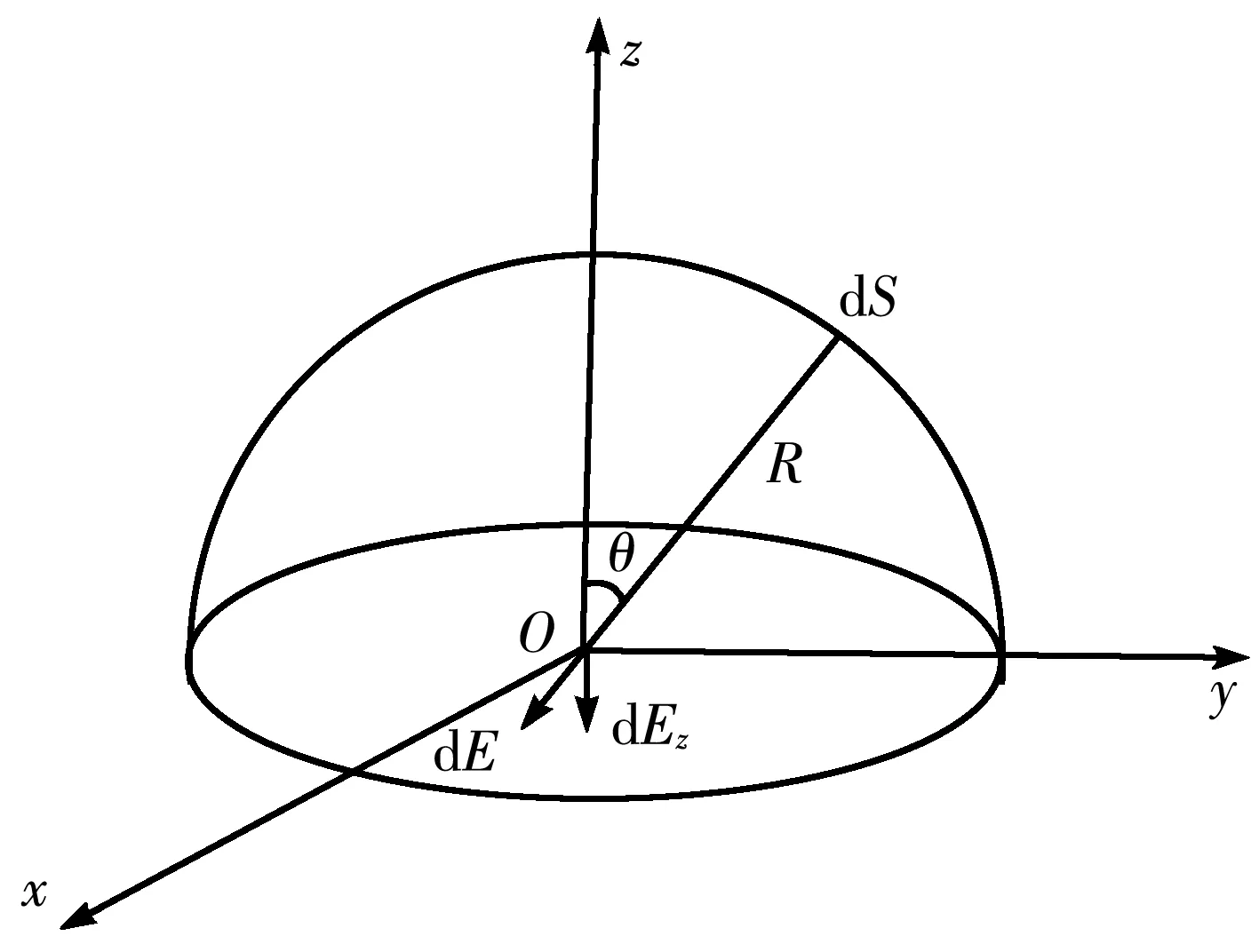
圖1 半球面球心處的電場
dS=R2sinθdθdφ
面積元dS所帶電荷量dq=σdS,在球心O處所產生的場強為
由對稱性分析可知,dE垂直于z軸方向的分量相互抵消,沿z軸方向的分量為dEz.
(1)
球心處電場強度的方向沿z軸負方向.
2.2 均勻帶電半球面軸線上一點P(0,0,z)的電場強度
圖2為場點P位于z軸上不同位置的幾種情況.
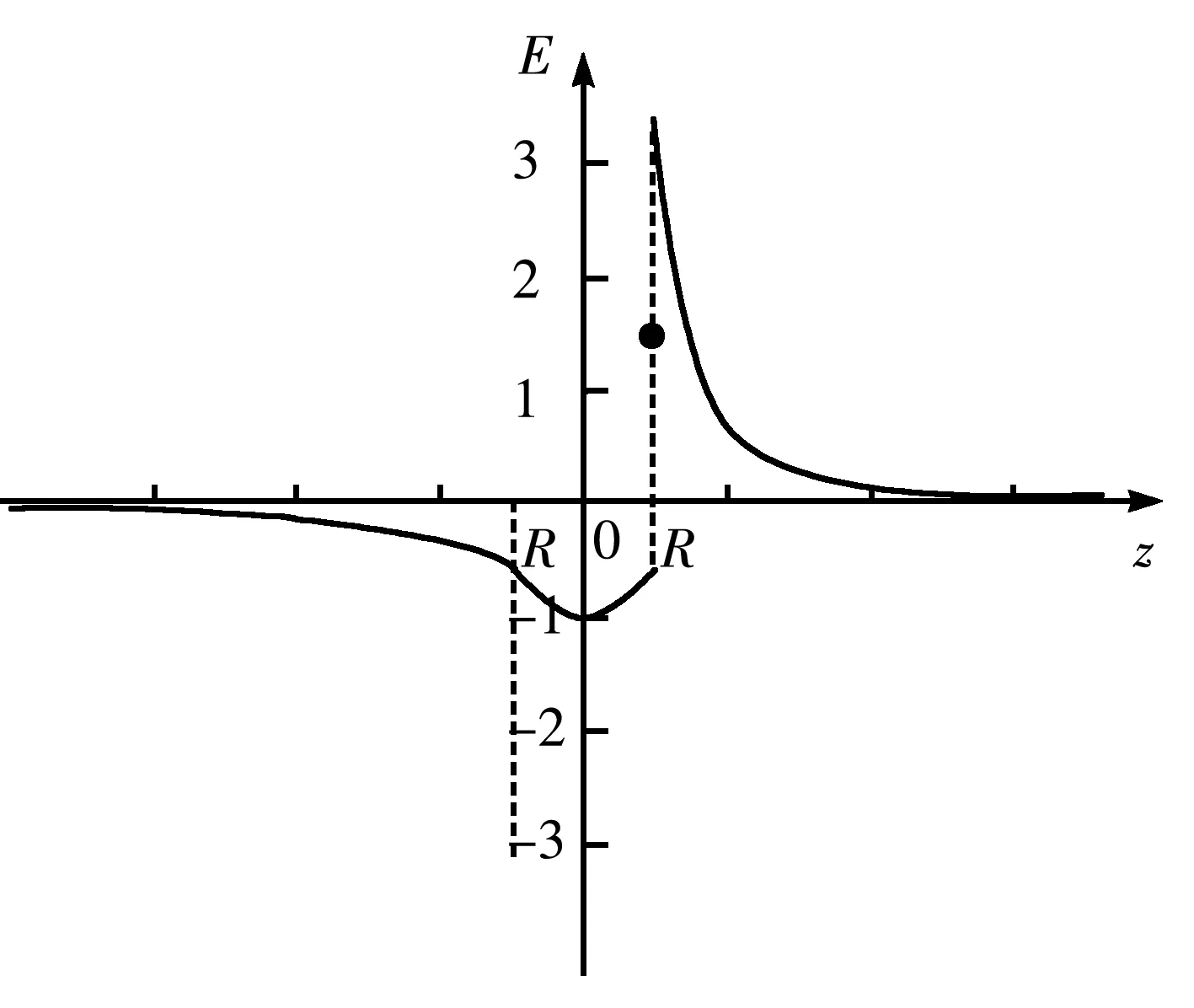
(1)若0 圖2 均勻帶電半球面P點處的電場 (2) 采用換元法,令 t2=R2-2Rzcosθ+z2 (3) 由式(3)可得 對式(3)兩邊分別求導得 tdt=Rzsinθdθ 代入式(2),得 (4) 該電場強度的方向沿z軸的負方向. (2)若z>R,場點P位于半球面外 (5) 該電場強度的方向指向z軸的正方向. (3)當z=R,即P點在半球面上時 (6) 場強方向沿z軸正方向. (4)若0>z>-R,場點P位于球內z軸負半軸,則 (7) (8) 電場強度的方向指向z軸的負方向. (5)若z<-R,被積函數與式(7)形式相同,在z=-R上沒有電荷,場強在這點連續,場強表達式與式(8)相同,只是z的取值范圍不同. (9) 該電場強度的方向沿z軸的負方向. (6)當z=-R,P點在z軸負半軸與球面交點上 (10) 場強方向沿z軸負方向. 綜上,均勻帶電半球面軸線上的電場強度分布為 圖3是用Matlab軟件模擬的均勻帶電半球面軸線上的電場強度E隨z變化的曲線. 圖3 均勻帶電半球面軸線上的E-z曲線 對于均勻帶電的半球面來說,電荷分布不像整個球面電荷那樣高度對稱分布,不能用高斯定理求解.其他求解的方法也有多種,最基本的方法還是利用場強疊加原理,再通過面積分求出帶電半球面軸線上的場強大小.類似的方法包括分割圓環帶法、電勢梯度法等.雖然這些解法稍有不同,最終都可歸為場強疊加方法的運用.當然,直接用場強疊加原理求解計算量相對要大些,但這種方法適用性最廣.同樣的解題思路也適用于求解均勻帶電球冠電場強度等相關問題.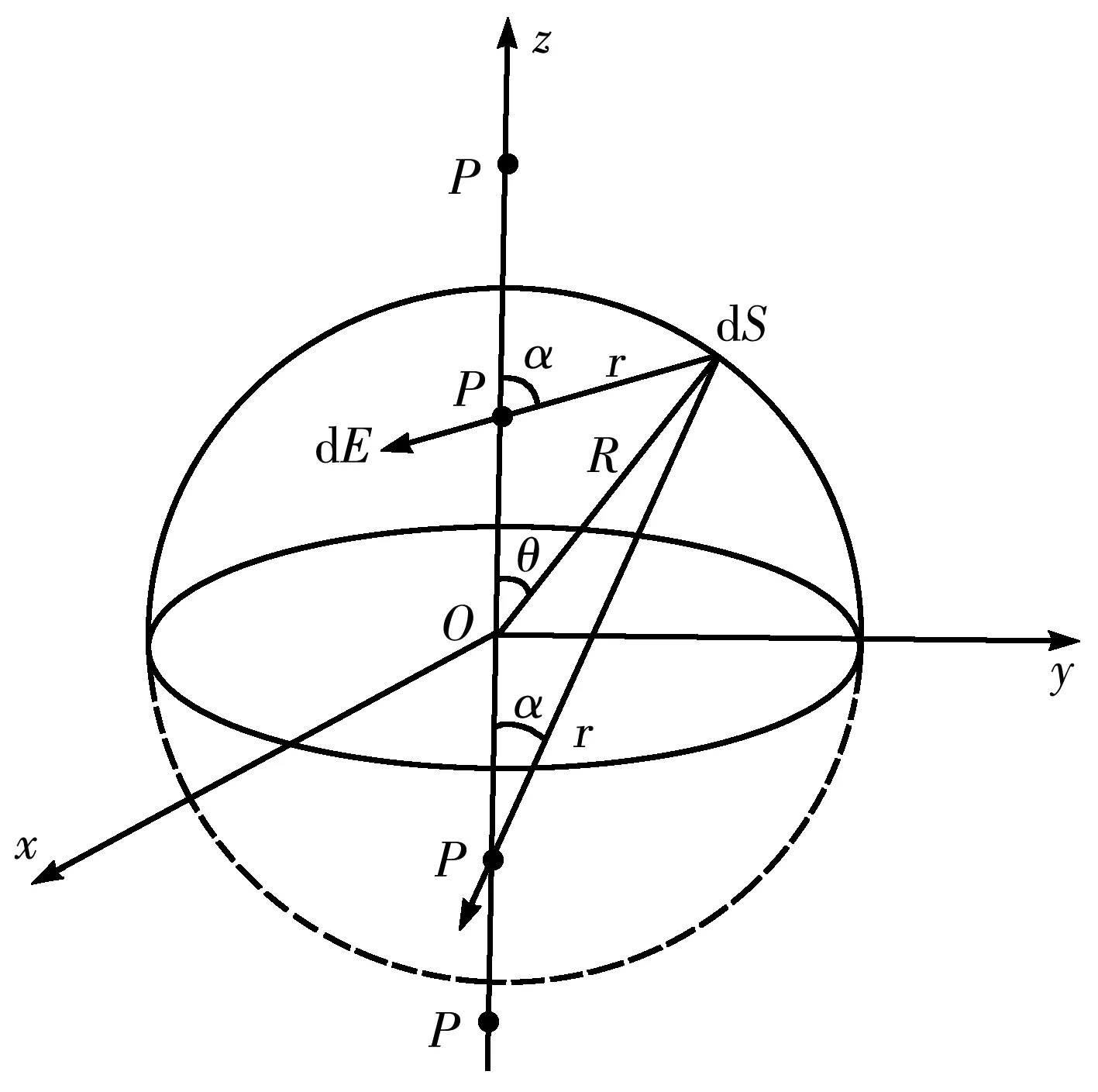
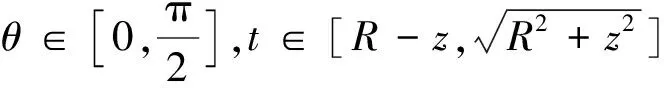
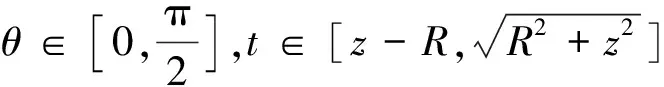
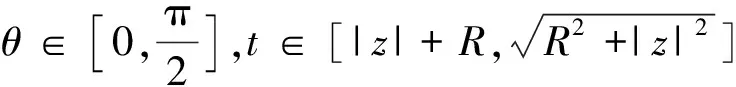
3 分析與結論
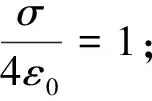
4 總結

