基于降階濾波器的鎖相方法

閔晶妍 陳紅兵

摘要 準確、快速檢測電網相位是并網變流器的關鍵技術，目前常用的閉環鎖相技術普遍存在動態延時長、濾波算法復雜、在電網受諧波污染時鎖相精度低等問題。針對上述不足，研究了降階濾波器及其分序機理和實現方法，在此基礎上，研究了基于降階濾波器的鎖相方法，并整定了環路濾波器的參數。實驗結果表明，所研究的鎖相技術在電網電壓跳變的情況下，相位檢測沒有暫態過程，鎖相精度不受電壓幅值突變的影響;在電網中存在3次諧波電壓時，鎖相精度提高了21%;頻率跳變不影響鎖相過程和鎖相精度，但是暫態過程約為20 ms，同時該鎖相環還能檢測單相電網的相位，較好地克服了常用的閉環鎖相技術存在的問題。

關 鍵 詞 降階濾波器;分序算法;環路濾波器

中圖分類號 TM46? ? ?文獻標志碼 A

Abstract The accuracy and rapidly detecting the phase of a grid is a key technology for grid-connected converters. There were some disadvantages in the common close loop PLL， such as a long dynamic response， complicated filter algorithms and low accuracy of the phase locked under distorted utility conditions. According to the above-mentioned disadvantages， the decomposing sequence method based on a reduce order filter， decomposing sequence mechanism and realization way have been analyzed. On that basis， the locked phase method based reduce order filter have been investigated. Parameters of the loop filter have been tuned. Lastly， the studied phase-locked technology has no transient response when the grid voltage dipped; Locked phase accuracy has been enhanced by 21% when the grid voltage component composes of the 3th harmonic wave voltage; The grid frequency fluctuation has no influence on locked phase accuracy and process， but there was a transient process of the 20ms. the investigated phase-locked technology can detect the phase of single-phase grid. The method has overcome the disadvantages of the common close loop PLL.

Key words reduce order filter; decompose sequence algorithm; loop filter

0 引言

準確、快速檢測電網相位是并網變流器的關鍵技術。相位檢測系統性能的優劣不僅關系到并網變流器的正常運行[1]，而且還影響新能源電力系統的安全穩定[2]。因此，研究相位檢測技術既有工程價值，也有學術意義。目前，相位檢測技術分為2大類，即開環鎖相技術和閉環鎖相技術。

開環鎖相技術沒有調節過程，鎖相過程短，這是開環鎖相技術的優點。但是，對于電壓嚴重畸變的電網，該方法不適合。閉環鎖相技術穩態性能好、電網適應性能強，是當前研究、應用的主流技術。閉環鎖相技術是運用反饋控制原理檢測電網的頻率和相位，它具備良好的幅值、相位和頻率自適應能力。常見的閉環鎖相技術多為基于同步旋轉坐標系的鎖相環（SRF-PLL）[3]。為了消除不對稱電壓分量對SRF-PLL的干擾，在鎖相環中引入低通濾波器，雖然低通濾波器降低了負序電壓分量對鎖相精度的影響，但是也降低了PLL的暫態響應速度[4]。因此，文獻[5-6]提出用滑動平均濾波（MAF）代替低通濾波器，以此提升鎖相環的動態性能。文獻[7]采用解耦思想將負序和正序分離，產生了雙同步坐標系鎖相環（DSRF-PLL）。在此基礎上，進一步衍生出能同時消除多個高次諧波影響的多解耦PLL。此后，相繼出現了基于二階廣義積分器的PLL[8]、基于自適應濾波器的PLL[9]等多種鎖相技術。上述鎖相技術采用低通濾波器或較復雜的濾波算法來降低負序分量或諧波分量的不良影響。如低通濾波器和二階廣義積分器的窄帶寬顯著影響了鎖相環的動態性能。如當電壓幅值變化時，鎖相過程長達2個基波周期;特別在頻率突變時，暫態過程更長，高達4個基波周期;當電網中存在諧波時，鎖相精度低。為了克服上述不足，本文研究了基于降階濾波器分序算法的鎖相技術。

下文將依次研究基于降階濾波器的分序算法、鎖相環的參數整定方法和性能。

1 基于降階濾波器的分序算法

本文研究的鎖相環，其框圖如圖1所示，三相電網電壓[uabc]經過Clarke變換，得到電壓分量[uα]和[uβ]，電壓分量[uα]和[uβ]經過分序算法處理，得到電壓的正序分量[u+αβ]，正序電壓分量經過Park變換，得到dq坐標系下的電壓分量[u+q]，用環路濾波器處理電壓分量[u+q]，再加上頻率的前饋量，得到電網頻率的估計值[ω0]，對頻率積分，得到電網相位[θ]。將[ω0]送入分序算法，使分序算法的頻率跟隨電網頻率變化，從而提高了分序精度。

本文采用降階濾波器實現分序，降階濾波器具備如下特征：在基波頻率[ω0]處，分序濾波器的幅頻特性為1，相頻特性為0;在其他頻率處，幅頻特性為0（迅速衰減為0或0以下）。文獻[10]研究表明，轉折頻率為[ωc]的降階濾波器滿足上述特性。[ωc]既決定降階濾波器的帶寬，也影響它的動態特性。綜合考慮濾波效果及其動態特性，文中[ωc]取314. 16 rad/s（電網額定頻率），分序算法如式（1）所示。

將鎖相環的參數歸一化之后，再根據式（5）整定環路濾波器的參數（即[kp=120]，[ki=800]）。將參數代入式（4），鎖相環的開環頻率特性如圖4所示。從圖4可知，鎖相環在200 Hz處的增益為-24 dB，表明對5次和5次以上的諧波（電網電壓的最大諧波分量是5次諧波）具有非常強的衰減作用。

3 實驗研究

本文分別研究了電網電壓幅值突變、頻率突變、電壓波形畸變和電網單相運行等4種工況的鎖相效果，具體效果如下。

當電壓幅值突降為原值的80%時，實驗結果如圖5所示。實驗結果表明，電壓幅值突變不影響鎖相過程和鎖相精度，在此工況下，相位檢測沒有暫態過程，鎖相精度也不受幅值突變的影響。

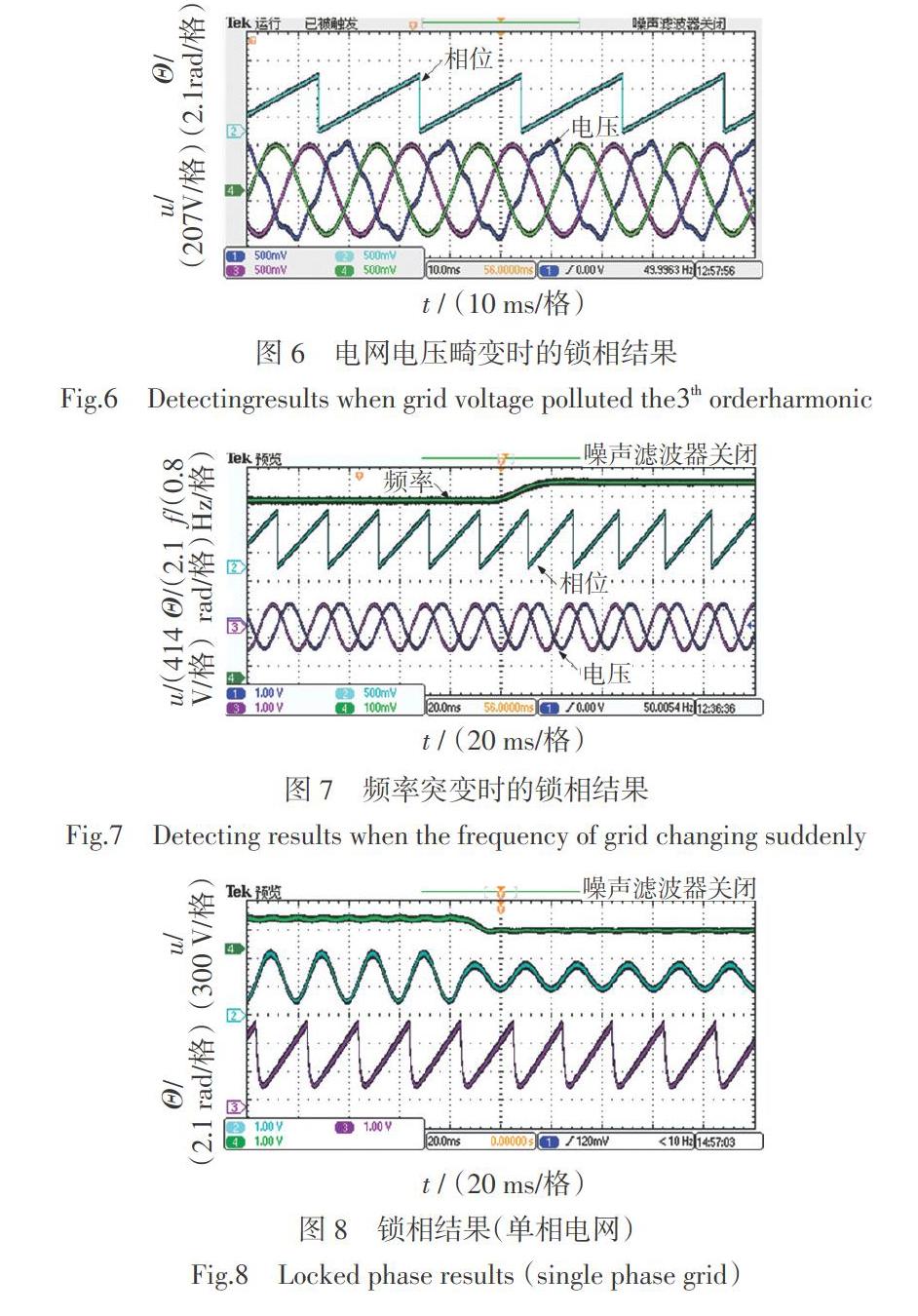
當C相電壓畸變（含3次諧波）時，實驗結果如圖6所示。經過分析和計算，鎖相精度提高了21%，由此說明，在電網電壓畸變時，本文研究的鎖相技術仍然滿足快速性、鎖相精度的要求。

當電網頻率由50 Hz突變為52 Hz時，鎖相環檢測的頻率[ω0]跟隨電網頻率變化，使分序算法能精確分離出電壓正序分量，根據正序分量檢測電網相位。雖然頻率突變不影響鎖相過程和鎖相精度，但是，檢測頻率有一個暫態過程，暫態時長約為20 ms，如圖7所示。

當用于檢測單相電網的相位時，其檢測結果如圖8所示。實驗結果表明，即使單相電網電壓的幅值突變，也不影響鎖相精度，并且相位檢測沒有暫態過程，這一特點與工況一類似。

4 結論

快速、準確檢測電網相位是并網設備的關鍵技術，為此，本文研究了一種基于頻率自適應降階濾波器的鎖相技術。研究結果表明本文所研究的鎖相方法提高了相位、頻率檢測精度，縮短了鎖相暫態過程。尤其針對頻率和幅值突變的工況，該鎖相法有效解決了SRF-PLL鎖相環的延時和電壓波形畸變導致閉環鎖相精度低的問題。

參考文獻：

[1]? ? 熊凌飛，韓民曉，姚蜀軍. 鎖相環對多端柔性直流穩定性作用分析及參數選擇研究[J]. 電工技術學報，2015，30（16）：203-212.

[2]? ? 曾正，趙榮祥，湯勝清，等. 可再生能源分散接入用先進并網逆變器研究綜述[J]. 中國電機工程學報，2013，33（24）：1-12.

[3]? ? 杜雄，劉延東，王國寧，等. 采用正弦幅值積分器的單同步參考坐標系同步信號檢測方法[J]. 電工技術學報，2015，30（8）：167-175.

[4]? ? LEE K J，LEE J P，SHIN D，et al. A novel grid synchronization PLL method based on adaptive low-pass notch filter for grid-connected PCS[J]. IEEE Transactions on Industrial Electronics，2014，61（1）：292-301.

[5]? ? GOLESTAN S，FREIJEDO F D，GUERRERO J M. A systematic approach to design high-order phase-locked loops[J]. IEEE Transactions on Power Electronics，2015，30（6）：2885-2890.

[6]? ? GOLESTAN S，FREIJEDO F D，VIDAL A，et al. A quasi-type-1 phase-locked loop structure[J]. IEEE Transactions on Power Electronics，2014，29（12）：6264-6270.

[7]? ? RODRIGUEZ P，POU J，BERGAS J，et al. Decoupled double synchronous reference frame PLL for power converters control[J]. IEEE Transactions on Power Electronics，2007，22（2）：584-592.

[8]? ? 辛振，趙仁德，陳晨，等. 基于雙二階廣義積分器-鎖頻環的異步電機同步角頻率估計方法[J]. 中國電機工程學報，2014，34（27）：4676-4682.

[9]? ? 孫士杰，閆海城. 基于新型二階廣義積分器的單相鎖相環設計[J]. 電力電子技術，2017，51（3）：111-113.

[10]? GUO X Q，WU W Y，CHEN Z. Multiple-complex coefficient-filter-based phase-locked loop and synchronization technique for three-phase grid-interfaced converters in distributed utility networks[J]. IEEE Transactions on Industrial Electronics，2011，58（4）：1194-1204.

[11]? 陳紅兵，閔晶妍. 基于正交信號發生器的單相鎖相環的研究[J]. 電力電子技術，2014，48（11）：23-25.