端部參數(shù)激勵下水中懸浮隧道錨索振動響應(yīng)分析

王金龍 巫志文

作者簡介：

王金龍（1988—），工程師，從事橋梁隧道施工管理工作;

巫志文（1984—），博士，講師，從事海洋橋梁隧道工程研究工作。

文章通過建立參數(shù)激勵系統(tǒng)理論模型進行理論分析和數(shù)值仿真計算，研究了端部參數(shù)激勵下水中懸浮隧道錨索的振動響應(yīng)，并對不同阻尼比、垂度、錨索長度、水流速度、傾斜角度、管體重浮比等關(guān)鍵敏感性參數(shù)對錨索的振動響應(yīng)影響作用進行分析，主要得到以下結(jié)論：在相同錨索長度、垂度的情況下，阻尼比越小，錨索中跨位移均方根值越大;隨著錨索長度、垂度的增加，錨索中跨位移均方根值也越來越大;隨著水流速度的不斷增加，錨索中跨位移均方根值呈現(xiàn)出先增大后減小，并最終趨于平穩(wěn)的狀態(tài);隨著傾斜角度的不斷增加，錨索中跨位移也隨之不斷增加，這表明選擇合適的傾斜角度對于控制結(jié)構(gòu)的振動響應(yīng)也很重要;在實際錨泊系統(tǒng)設(shè)計時，可以通過增加預(yù)張力的方式來控制錨索的運動響應(yīng)，但增加預(yù)張力會導(dǎo)致錨索固有頻率的改變，使結(jié)構(gòu)共振頻率比增加，導(dǎo)致其疲勞屈服損傷加深。

懸浮隧道;錨索;參數(shù)激勵振動

U459A351195

0 引言

隨著現(xiàn)代科技與社會的發(fā)展，生產(chǎn)和生活水平的提高，人們越來越渴望更加高效、便捷的交通方式，正是這樣的需求促進著懸浮隧道等新型交通設(shè)施的提出和研究。

水中懸浮隧道，學(xué)名Submerged floating tunnel（SFT），是依據(jù)阿基米德原理（hydrostatic thrust）采用靜壓推力構(gòu)思出來的新穎的交通結(jié)構(gòu)[1]，以隧道的形式穿越大型深水域，因此更廣泛使用的名字是阿基米德橋。它的主體是滿足公路及鐵道交通要求的管狀結(jié)構(gòu)，由海床上的錨固系統(tǒng)或水上浮箱等方式加以固定，懸浮在水中一定深度，與兩岸的建筑結(jié)構(gòu)相連接，受自身重力、水體浮力和支撐結(jié)構(gòu)的錨固力來穩(wěn)定在構(gòu)筑位置上。

根據(jù)目前的研究設(shè)計，懸浮隧道最有可能采取的是墩柱式、錨固式這兩種支撐體系。關(guān)于這兩種體系的相關(guān)分析，學(xué)者[2-5]在結(jié)合了波浪、海流、地震等因素以及其他環(huán)境作用下，研究了它們的穩(wěn)定性和相應(yīng)的承載力。比較重要的因素是環(huán)境動荷載作用，因此國內(nèi)外專家學(xué)者在這方面的研究也更為廣泛。

P.Fogazzi和F.Perotti[6]嘗試建立墨西拿海峽水中懸浮隧道的有限元模型，由于存在變化的軸力作用，需要研究錨索單元的橫向振動，并將實際應(yīng)用中的錨固系統(tǒng)模型化，視為兩個桿件面積和柔度都相等的5個自由度的平面鉸接桿單元。為了得到該單元剛度矩陣還需要一些其他假設(shè)：可忽略轉(zhuǎn)動及橫向位移;軸向變形足夠小，并且不沿桿長改變，是關(guān)于節(jié)點位移的一個二次函數(shù);材料是彈性的。為了完善模型，在桿件單元底部的數(shù)值和水平方向分別設(shè)了兩個彈簧和兩個平行于彈簧的線性阻尼。雖然其地震激勵下的動力響應(yīng)分析結(jié)果不足以配合工程要求，但仍非常具有參考意義。

麥繼婷等[7]采取了另一種簡化方式，為計算參數(shù)激勵頻率對張力腿一階渦激動力響應(yīng)的影響，將張力腿簡化為豎向簡支梁有如下假設(shè)：張力沿錨桿方向的變化很小;將參數(shù)激勵項的頻率視為與車輛響應(yīng)頻率相同;以流向為x軸正方向。在此假設(shè)下應(yīng)用渦激振動方程，考慮非線性流體阻尼、參數(shù)激勵，結(jié)合伽遼金法、數(shù)值積分法，可以達到計算目的。

秦銀剛[8]等最先使用Lyapunov函數(shù)計算參數(shù)激勵下張力腿穩(wěn)定性，包括振動階次、張力腿軸向剛度、參數(shù)激勵頻率、張力腿長度、初始張力大小、動張力系數(shù)對張力腿穩(wěn)定性的影響。

懸浮隧道的振動參數(shù)問題一直是可行性研究的重點。懸浮隧道豎向的穩(wěn)定主要是靠自身的重力和錨索的拉力來平衡其浮力，而其水平方向的平衡則主要是靠斜拉錨索的拉力來平衡其所受到的波浪力和水流力，因此，錨索的穩(wěn)定問題也就顯得越來越重要了[9]。由此，研究懸浮隧道錨索在渦激振動下的穩(wěn)定性，具有一定的工程應(yīng)用價值。

本文詳細(xì)研究了端部參數(shù)激勵下水中懸浮隧道錨索振動分析，通過理論分析和數(shù)值仿真計算，對不同阻尼比、垂度、錨索長度、水流速度、傾斜角度、管體重浮比等關(guān)鍵敏感性參數(shù)對結(jié)構(gòu)的振動響應(yīng)影響作用進行深入研究。

1 理論基礎(chǔ)

1.1 建立參數(shù)激勵系統(tǒng)理論模型

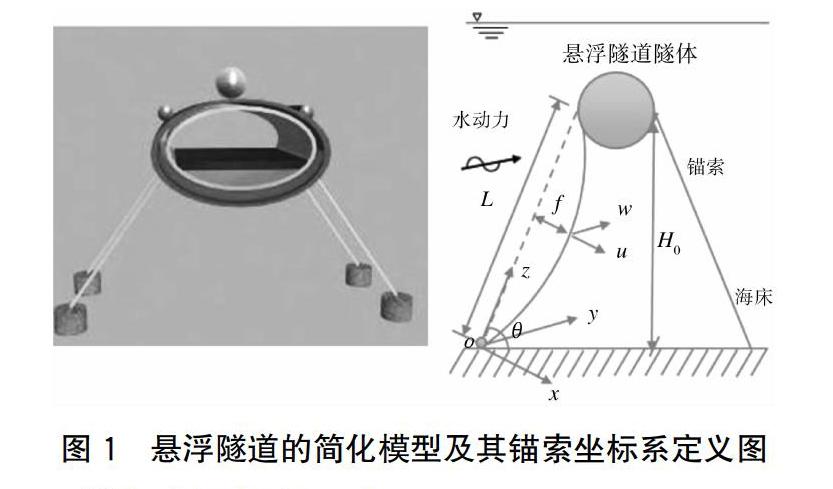
根據(jù)實際錨索設(shè)計，建立如圖1所示的坐標(biāo)系。

錨索端部激勵方程：

Z=ZccosωTt（1）

式中：Zc——幅值;

ωT——頻率。

此外有以下假設(shè)：不考慮錨索的抗彎剛度;考慮水體附加慣性力以及水體阻尼力;考慮垂度。

關(guān)于垂度的討論：錨索的跨中垂度f應(yīng)小于錨索的無應(yīng)力長度L的1/8。假設(shè)錨索在初始狀態(tài)處于拋物線型，則有[10]：

x=4fzL1-zL（2）

式中：LE——靜力狀態(tài)下錨索長度;

θ——傾角;

E——彈性模量;

A——橫截面積;

m——無應(yīng)力狀態(tài)下單位長度質(zhì)量。其中：

LE=L1+8f/L2

（3）

設(shè)靜力狀態(tài)下錨索的張力為：

T0=T0（s）（4）

式中：s——弧長坐標(biāo);

u——沿錨索軸向的法線方向由靜力平衡位置開始的位移，可以用來表示動荷載下的動力構(gòu)型。

由相關(guān)原理可以得到最終的錨索振動方程：

m2ut2+Csut-ΔH2xz2-H0+ΔH2uz2=FD

（5）

ΔH=EALEZccosωTt+8fL2L0udz+12L0uz2dz

（6）

f=γfVsL2cosθ8T0（7）

式中：Cs——錨索黏性阻尼系數(shù);

FD——錨索振動引起的水體對其的作用力;

H0——沿z向的錨索初張力。假設(shè)垂度很小，有T0≈H0，且ds≈dz;

ΔH——振動引起的附加錨索張力;

f——錨索跨中垂度;

γf——錨索浮容重;

Vs——錨索單位長度的體積。

考慮水體的附加慣性力和阻尼力時，由于錨索直徑與入射波的波長相比尺度非常小，計算水體的作用力時可以應(yīng)用Morison方程。用附加慣性力和水體阻尼力之和來表示錨索橫向振動產(chǎn)生的水體對單位長度的作用力：

FD=-πD24ρWCmü-12ρWDCD||（8）

式中：ρW——水的密度;

D——錨索外直徑;

CD——拖拽力系數(shù)，取CD=0.7;

Cm——附加質(zhì)量系數(shù)，取Cm=1。

考慮到錨索的垂跨比很小，可以近似地取標(biāo)準(zhǔn)線的振動模態(tài)：

uz，t=∑Nn=1untsinnπzL

（9）

將式代入，采用伽遼金法化簡，可得：

L0Rz，tsinjπzLdz=0 j=1，2，…，∞（10）

式中：R（z，t）——留函數(shù)。

Tagata由實驗指出，對于張緊的弦，在其端部激勵振動中占主要部分的是基本模態(tài)，因此可將下式作為一階振動模態(tài)的化簡式：

ü+2ωsξs+ω2s+EAπ2mL2LEZccosωTtu+24fEAπmL3LEu2+ EAπ44

mL3LEu3+32fEAmL2LEπZccosωTt+2DnL·m=0（11）

其中：

Dn=12ρWDCDL0sinπzL2sgnsinπzLsinπzLdzm=m+πD24ρWCm，為單位長度質(zhì)量與附加質(zhì)量之和;

ω2s=T0mπL2+512f2EAmL3LEπ2

，ωs為一階固有頻率;Cs=2mωsξs，ξs為阻尼比。

若不考慮垂度的影響，也可以得到不含垂度的振動方程：

ü+2ωsξs+ω2s+EAπ2mL3ZccosωTtu+EAπ44mL4u3+2DnL·m=0（12）

若將式（11）與式（12）做比較可以發(fā)現(xiàn)，不考慮垂度則振動方程中少了u2項和32fEAmL2LEπZccosωTt項。u2項是為了使錨索振動偏離平衡位置，32fEAmL2LEπZccosωTt項表示端部激勵在振動方程中即充當(dāng)參數(shù)激勵的作用，也充當(dāng)外部振動荷載。

若對比錨索在空氣中的振動方程，可得：

ü+2ωsξs+ω2s+EAπ2mL2LEZccosωTtu+24fEAπmL3LEu2+EAπ4mL3LEu3+32fEAmL2LEπZccosωTt=0（13）

這個方程可以看作是關(guān)于錨索自身質(zhì)量的部分，另一部分是水中的附加質(zhì)量，此外錨索還受阻尼力作用。計算錨索跨中垂度需要利用浮容重，因此若其他條件不變，水中的垂度會小于空氣。

1.2 方程數(shù)值解的求解

為求非線性常微分方程的數(shù)值解，考慮采用Matlab中的ode45函數(shù)。ode45函數(shù)采用的方法是4階RungeKutta算法，用5階公式做誤差估計來調(diào)節(jié)步長，是一種自適應(yīng)步長（variablestep變步長）的常微分方程數(shù)值解法，也是求非剛性常微分方程數(shù)值解的首選方法。RungeKutta法是一種高精度單步算法，易于改變步長，比較穩(wěn)定，在工程上應(yīng)用廣泛，但計算量較大。四階RungeKutta法精度更高，也是最為常用的一種。

由于誤差累計，Matlab中的ode45是經(jīng)過改造的，其基礎(chǔ)是經(jīng)典的4階RungeKutta公式[11]，見式（14）：

k1=fxi，yi

k2=fxi+12，yi+h2k1

k3=fxi+12，yi+h2k2

k4=fxi+1，yi+hk3

yi+1=yi+h6k1+2k2+2k3+k4

（14）

求解高階常微分方程時，不能直接應(yīng)用ode45求解，需先將方程化為一階常微分方程組。對于式（13），用兩個新的變量來代換u和，才可以達到這一目的。為了方便表示清晰，先將方程簡化為式（15）：

ü+A+Btu2+Cu2+Du3+Et=0（15）

再分別設(shè)u1=u，u2=，可將原二階常微分方程轉(zhuǎn)化為如下一階常微分方程組，見式（16）：

1=u2

2=-Au2+Btu21+Cu21+Du31+Et

（16）

式（16）即成為可以由ode45求解的形式。

2 數(shù)值分析與結(jié)果

錨索端部參數(shù)激勵振動方程的計算主要通過Matlab編程實現(xiàn)，采用四階Runge-Kutta法計算式（13）的數(shù)值解。基本參數(shù)的確定是根據(jù)國外懸浮隧道設(shè)計方案中的參數(shù)來選取適當(dāng)范圍，并設(shè)定相應(yīng)的參數(shù)。取標(biāo)準(zhǔn)參數(shù)如表1所示。

2.1 特定參數(shù)的變化對振動的影響

本章節(jié)通過理論分析和數(shù)值仿真計算，對不同阻尼比、垂度、錨索長度、水流速度、傾斜角度、管體重浮比等關(guān)鍵敏感性參數(shù)對結(jié)構(gòu)的動力響應(yīng)影響作用進行深入研究。

2.1.1 阻尼比、垂度及錨索長度的影響

根據(jù)國外設(shè)計方案中的擬建數(shù)值，阻尼比取值為0.001 6。在阻尼比參數(shù)的一系列對比中，選取的變化范圍是0.001 0～0.002 2。

如圖2所示，在三種不同的阻尼比的情況下，均表現(xiàn)出當(dāng)錨索長度<180 m時，錨索中跨位移均方根值保持在一個較穩(wěn)定的值，當(dāng)長度超過180 m，錨索中跨位移均方根值出現(xiàn)陡增式的增長。另一方面，比較不同的阻尼比可以發(fā)現(xiàn)，在相同的錨索長度下，阻尼比越大，錨索中跨位移均方根值越小。

隨著錨索長度地不斷增大，錨索中跨位移均方根值也在不斷增大，這說明錨索的長度對結(jié)構(gòu)的穩(wěn)定性有著重要的影響，長度超過一定限度范圍，將降低結(jié)構(gòu)的穩(wěn)定性，并且這種對穩(wěn)定性的破壞呈現(xiàn)出指數(shù)型的增長。另一方面，隨著錨索阻尼比的增大，錨索中跨位移不斷減少，說明阻尼比對結(jié)構(gòu)穩(wěn)定性有著一定影響，并且阻尼比越大，結(jié)構(gòu)越穩(wěn)定。

如圖3所示，在三種不同阻尼比的情況下，隨著錨索垂度的增加，錨索中跨位移均方根值也在不斷地增大。另一方面，比較不同的阻尼比可以發(fā)現(xiàn)，在垂度相同的情況下，阻尼比越大，錨索中跨位移均方根值越小。

因此在實際工程應(yīng)用中，可以通過合理設(shè)計及選取懸浮隧道錨索材料、調(diào)節(jié)適當(dāng)?shù)腻^索長度、垂度關(guān)鍵參數(shù)，在錨索及隧體安裝阻尼器等方式增加結(jié)構(gòu)的阻尼比，從而提高懸浮隧道錨泊系統(tǒng)整體的穩(wěn)定性和安全性。

2.1.2 傾斜角度的影響

如圖4的計算結(jié)果所示，隨著水流速度的增大，錨索中跨位移也有著較大的波動。當(dāng)水流速度達到約2 m/s時，錨索動力響應(yīng)最強烈，錨索中跨位移達到最大值。當(dāng)水流速度繼續(xù)增大時，錨索中跨位移則迅速減小直至穩(wěn)定狀態(tài)。另外，隨著傾斜角度的不斷增加，錨索中跨位移也隨之不斷增加，這表明選擇合適的傾斜角度對于控制結(jié)構(gòu)的動力響應(yīng)也很重要。

2.1.3 管體重浮比的影響

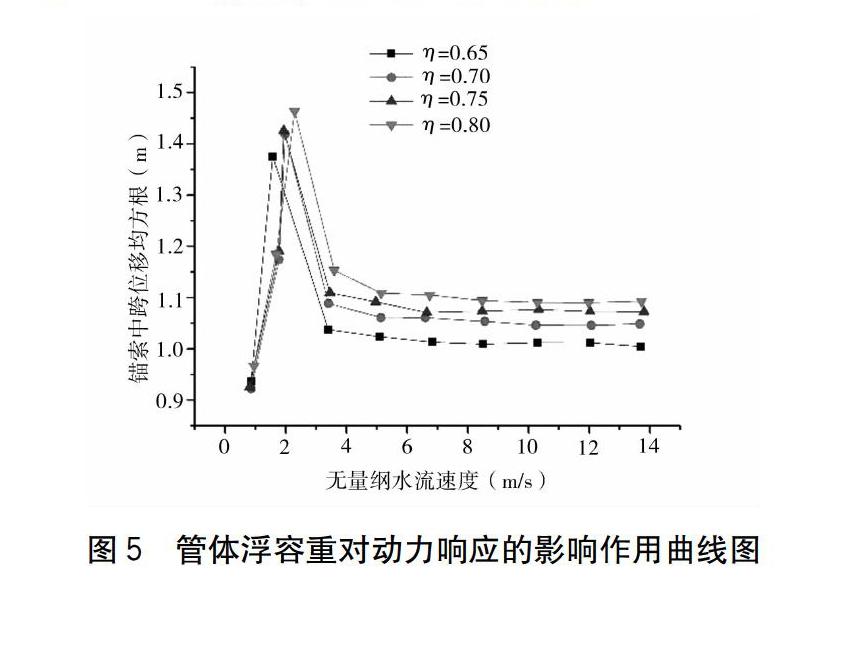
管體重浮比是懸浮隧道設(shè)計中一個很重要的設(shè)計參數(shù)，因此有必要對其進行相應(yīng)的研究。如圖5所示，隨著水流速度的增大，錨索中跨位移均方根值表現(xiàn)出先不斷增大，后逐漸減小并最終趨于平穩(wěn)的趨勢。大約在水流速度為2 m/s時，錨索中跨位移達到最大值。另一方面，在相同水流速度的條件下，隨著重浮比的增加，錨索中跨位移均方根值也隨之不斷減小，這說明重浮比也會顯著影響控制結(jié)構(gòu)的動力響應(yīng)。

2.1.4 預(yù)張力和頻率比的影響

如圖6所示，在三種不同預(yù)張力下，錨索中跨位移均方根值都是先增加后減小，并且隨著預(yù)張力的增大，峰值處的ωs/ω1值也在變大。對比圖6和圖7可以發(fā)現(xiàn)，當(dāng)ωs/ω1=1時，三種預(yù)張力下其峰值大小相差不大，但當(dāng)ωs/ω1=2，預(yù)張力為T0時，其峰值明顯比預(yù)張力為1.4T0和1.8T0時的值要增大很多。

由此可見，在實際錨泊系統(tǒng)設(shè)計時，可以通過增加預(yù)張力的方式來控制錨索的動力響應(yīng)，但是務(wù)必注意的是，增加預(yù)張力會導(dǎo)致錨索固有頻率的改變，使結(jié)構(gòu)共振頻率比增加，但是會導(dǎo)致其疲勞屈服損傷加深。因而，工程設(shè)計應(yīng)同時考慮結(jié)構(gòu)運動響應(yīng)及屈服強度，利用結(jié)構(gòu)優(yōu)化控制策略來確定合理的預(yù)張力。

3 結(jié)語

文章詳細(xì)研究了水中懸浮隧道錨索端部參數(shù)振動，通過理論分析和數(shù)值仿真計算，對不同阻尼比、垂度、錨索長度、水流速度、傾斜角度、管體重浮比等關(guān)鍵敏感性參數(shù)對結(jié)構(gòu)的動力響應(yīng)影響作用進行深入研究，主要得到以下結(jié)論：

（1）在相同錨索長度、垂度的情況下，阻尼比越小，錨索中跨位移均方根值越大;隨著錨索長度、垂度的增加，錨索中跨位移均方根值也越來越大。

（2）隨著水流速度的不斷增加，錨索中跨位移均方根值呈現(xiàn)出先增大后減小，并最終趨于平穩(wěn)的狀態(tài)。

（3）隨著傾斜角度的不斷增加，錨索中跨位移也隨之不斷增加，這表明選擇合適的傾斜角度對于控制結(jié)構(gòu)的動力響應(yīng)也很重要。

（4）在實際錨泊系統(tǒng)設(shè)計時，可以通過增加預(yù)張力的方式來控制錨索的動力響應(yīng)，但是務(wù)必注意的是，增加預(yù)張力會導(dǎo)致錨索固有頻率的改變，使結(jié)構(gòu)共振頻率比增加，但是會導(dǎo)致其疲勞屈服損傷加深。

[1]蘇志彬，孫勝男.參數(shù)激勵下水下懸浮隧道錨索的穩(wěn)定性研究[J].中南大學(xué)學(xué)報，2013，44（6）：2 549-2 553.

[2]董滿生，趙佳佳，牛忠榮，等.隨機地震激勵作用下水中懸浮隧道錨索的動力響應(yīng)[J].合肥工業(yè)大學(xué)學(xué)報（自然科學(xué)版），2013，36（1）：74-78.

[3]DONG M，MIAO G，YONG L，et al.Effect of escape device for Submerged Floating Tunnel（SFT）on hydrodynamic loads applied to SFT[J].Journal of Hydrodynamics，Ser. B，2012，24（4）：609-616.

[4]Luca Martinelli， Gianluca Barbella， Anna Feriani. A numerical procedure for simulating the multi-support seismic response of submerged floating tunnels anchored by cables[J].Engineering Structures，2011（33）：2 850-2 860.

[5]田雪飛，董滿生，逄煥平.海洋內(nèi)波和洋流聯(lián)合作用下水中懸浮隧道的動力響應(yīng)[J].應(yīng)用數(shù)學(xué)和力學(xué)，2014，1（35）：71-79.

[6]Di Pilato M， Perotti F，F(xiàn)ogazzi P. 3D dynamic response of submerged floating tunnels under

seismic and hydrodynamic excitation[J]. Engineering structures，2008，30（1）：268-281.

[7]麥繼婷，楊顯成，關(guān)寶樹.懸浮隧道和支撐結(jié)構(gòu)的響應(yīng)分析[J].鐵道工程學(xué)報，2009（7）：67-71.

[8]秦銀剛，周曉軍.張力腿型懸浮隧道渦激響應(yīng)影響因素分析[J].鐵道工程學(xué)報，2009（1）：77-81.

[9]陳健云，王變革，孫勝男.水流作用下懸浮隧道錨索的動力響應(yīng)[J].工程力學(xué)，2007，24（10）：229-234.

[10]孫勝男，蘇志彬，白衛(wèi)峰.軸向激勵下懸浮隧道錨索參數(shù)振動分析[J].工程力學(xué)，2011，6（28）：170-174.

[11]趙佳佳.地震作用下懸浮隧道的動力響應(yīng)研究[D].合肥：合肥工業(yè)大學(xué)，2013.