“泛在智能”時代熱力學與統計物理教學設計實踐
——以卡諾循環教學設計為例

塔金星

(東北林業大學理學院，哈爾濱 150040)

在熱力學與統計物理的卡諾循環教學中，理想氣體的卡諾循環是重點教學內容。在分析過程中，會利用到很多公式，能夠考察學生對功的公式的理解程度。等溫過程中需要利用到物態方程，絕熱過程中涉及焦耳定律、泊松方程、絕熱方程的合理運用，這兩個過程還都要用到數學中的微積分公式。

隨著“泛在智能”時代的到來，越來越多的教師已經完全采用了課件等多媒體形式進行授課，優點顯而易見，包含豐富多彩的圖片、音頻、視頻，在聽覺和視覺等方面可以強烈刺激學生的感官，引起學生共鳴。但對學生的思維引導有所欠缺，除了利用課件授課以外，傳統板書教學依然很有必要。

1 多媒體課件內容設計

教學從基本概念講起，然后過渡到理論公式的推導及其意義分析。當基本概念和圖示較多時，不適合傳統板書教學。為提高課堂教學效率，該部分采用課件形式進行授課，具體設計如下：

①循環：經歷一系列變化后又回到初始狀態的整個過程。

②表示法：P-V圖中的封閉曲線，如圖1、圖2所示。

③分類：正循環(系統對外做功)、逆循環(外界對系統做功)。

④代表：卡諾循環、斯特林循環，如圖1、圖2 所示。

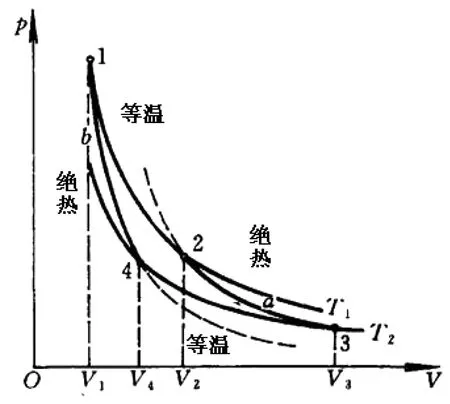
圖1 卡諾循環

圖2 斯特林循環

卡諾循環由兩個準靜態的等溫過程與兩個準靜態的絕熱過程構成。斯特林循環由兩個準靜態的等溫過程與兩個準靜態的等體過程構成。在這部分課堂教學中，只分析卡諾循環，學生學會了分析方法后，要求學生課后獨立分析斯特林循環，鞏固所學內容。還可以添加熱機介紹視頻，使學生更直觀地了解熱機工作情況。

2 傳統板書內容設計

以1 mol理想氣體為研究對象，分別分析卡諾循環中等溫過程與絕熱過程的做功和傳熱。

2.1 等溫過程

利用物態方程、準靜態做功微分式、熱力學第一定律微分式聯立可得：

(1)

討論：當體積膨脹時，做功為負，系統吸收熱量保持等溫。當體積壓縮時，做功為正，系統放熱保持等溫。這一部分難度不大，學生能夠理解。

2.2 絕熱過程

思維引導主要體現在定律及公式的合理運用，需要利用作功公式、泊松方程、絕熱指數與等容熱容關系、積分技巧。

方法一：由絕熱方程pVγ=C變形可得：

(2)

利用積分技巧、絕熱方程、絕熱指數與等容熱容關系可得：

(3)

在得出具體結果前，為啟發學生思考，提出了引導性問題：

①在計算功時，為什么用泊松方程中的形式去表示壓強P？而不用物態方程？

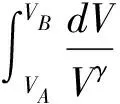
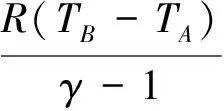
⑤結果CV(TB-TA)有具體的物理意義嗎？進而引出更簡潔的計算方法二。

方法二：絕熱過程無熱量交換，根據熱力學第一定律及焦耳定律可得：

(4)

積分結果與式(3)相同。該方法不需要復雜的數學積分及泊松方程等難點知識，計算過程簡潔明了，更能體現物理思維過程。

3 結語

“泛在智能”時代可以為教師教學提供豐富多彩的課程背景資料和良好的授課環境。但熱力學與統計物理課程理論性較強，公式繁多，除了借助現代化技術手段的多媒體課件以外，傳統的板書教學仍然是很主要的教學形式。針對具體的教學內容和學生的接受程度，多媒體課件和板書教學的應用比例需不斷調整，不能完全依賴多媒體。