高等數學教學效果優化策略研究

佟珊珊，陳 森，路 寬

(1.陜西師范大學 數學與統計學院，西安 710119；2.西北工業大學 力學與土木建筑學院，西安 710072)

1 高等數學教學存在的問題

1.1 學生對高等數學認知不足

與初等數學相比，高等數學具有更高的抽象性、概括性。高等數學開設在大學一年級課程中，學生很難理解高等數學中的抽象表述并靈活運用，例如極限的“ε-δ”語言等知識。在課堂教學中，教師通常更注重知識的傳遞，理論證明往往占用大部分課堂時間。但學生對理論證明的興趣不高、關注度不夠，難以真正理解定義及定理所蘊含的數學真理，只能死記硬背概念或結論，不能活學活用，這在一定程度上挫傷了學生學習高等數學的積極性。

1.2 傳統教學方式存在局限性

部分教師為了追求教學內容的嚴謹性，強化核心知識的講解，主要采用傳統的教學方法。傳統教學方式以教師講解為主，教師與學生課上互動較少，學生參與感不足。對于較為復雜的定理證明，學生很難跟上教師的講授思路。教師與學生課下交流不足，不能及時了解學生對知識的理解和運用情況。此外，在高等數學教學過程中，教師忽視在教學中融入趣味性元素，難以激發學生的學習熱情。

1.3 缺乏數學實際應用的探究

高等數學具有高度的抽象性，學生不了解高等數學知識在實際問題中發揮的作用。“用”的概念不強，“學”的動力不足。教師注重對學生計算能力的鍛煉，但在一定程度上忽視了應用能力的培養。傳統的考核制度側重于利用公式直接計算，而對利用所學知識解決物理、經濟、工程等實際問題的能力考核評價較少，導致學生不夠重視對高等數學實際應用能力的訓練。

2 高等數學教學效果優化策略

2.1 融入數學史的學習

數學史是研究數學發展和規律的一門學科，它不僅追溯數學史料，而且蘊含著深刻的數學思想。在高等數學授課過程中融入數學史，適當介紹數學家的軼事、數學定理證明的發展歷史等，能夠活躍課堂氣氛，增強學生學習數學的興趣。通過學習數學史，也能讓學生認識到數學來源于生活，是認識世界的重要工具。此外，通過了解數學家的生平，學生能夠學習數學家們在追求數學真理過程中展現出的優秀品質，有助于培養學生的數學素養。

教師可以在講授定義、定理前，通過相關的數學問題、數學家軼事作為引言，將數學史融入到教學中[1]。例如，在講授極限的概念時，可以借助經典問題吸引學生的關注，提高教學效果。如《莊子·天下篇》中的“一尺之棰，日取其半，萬世不竭”。意思是一尺長的木棍，每天截取它的一半，把每次截取的長度排成數列，無限制地進行下去，當天數無限增加趨于正無窮時，截掉的長度就無限接近于零，則零就是這個數列的極限。這個故事生動形象地描述了極限的概念，便于學生理解和掌握數學問題。

2.2 結合問題驅動教學模式

問題驅動教學模式是以問題為導向的教學方法，通過設立一系列環環相扣的問題，激發學生的探索熱情，引導學生在主動分析問題、解決問題的過程中學習新知識。高等數學中許多概念、定理的得出都是受問題驅動而展開的猜想、假設、推理和驗證。因此，在高等數學教學過程中適當采用問題驅動的教學模式有利于提高學生的學習熱情和學習動力，培養學生自主學習，善于探索和勇于實踐的能力。

在教學過程中，教師可遵循抽象內容具體化、以舊知識帶動新知識、聯想類比等基本原則設立問題情境[2]。例如，在導數定義的教學活動中，要以學生為主體，教師為主導，知識為主線。以恰當的問題為紐帶，給學生創設自主探究、合作交流的空間，指導學生類比探究形成導數概念，讓學生在參與中獲取知識，拓展思維。

以如下問題作為引言，即“同學們在乘坐高鐵時，在高鐵車廂前面可以看到一塊顯示高鐵時時運行速度的電子顯示屏，這樣的瞬時速度該如何計算”。將這一問題轉化為數學問題，如圖1所示。

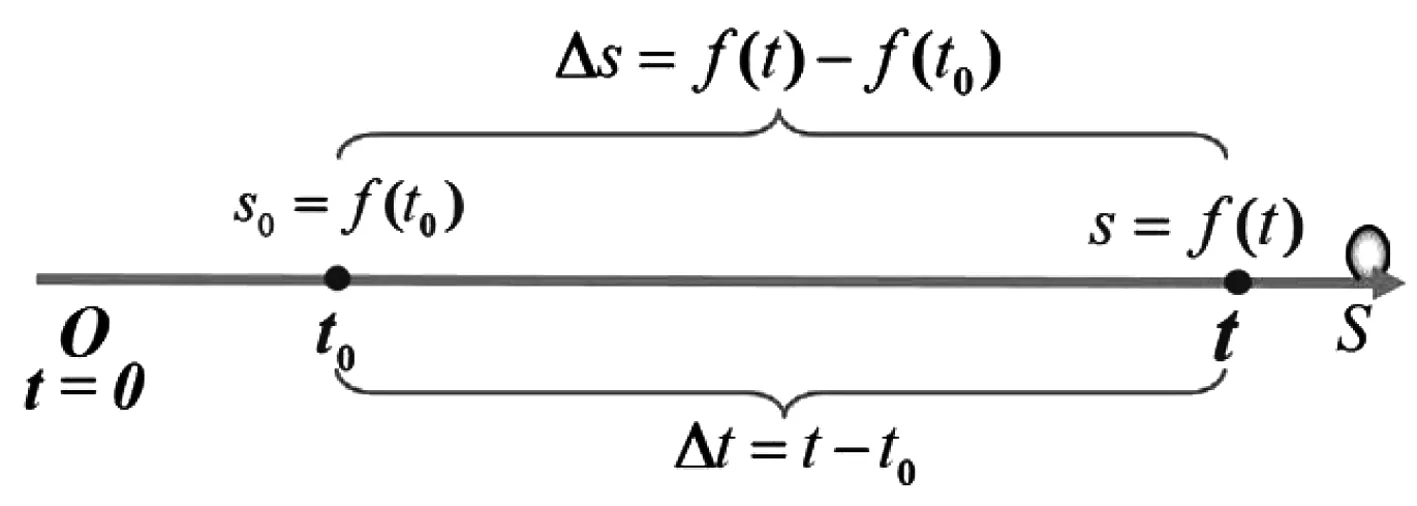
圖1 瞬時速度計算

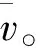
從平均速度循序漸進到瞬時速度，遵循知識的延續和遷移，從舊知識出發激發了學生的學習興趣。通過實際問題鞏固學生對導數物理意義的掌握，加深對知識的理解。

2.3 有效利用思維導圖

思維導圖是簡單、高效表達發散性思維的工具，通過圖文并重的方法將各級主題之間的相互聯系清晰地展現出來[3]。學生能夠掌握單一的知識點，但很難建立起各個章節之間知識點的聯系，在解題過程中思維不夠靈活和拓展。針對這一問題，教師在復習總結時，應運用知識思維導圖建立各章節知識點框架，幫助學生建立一條能夠貫穿各章節的知識線，完成知識點的銜接，提高學生對高等數學的綜合認識，培養學生靈活運用知識點解決問題的能力。

以一元函數微分學為例，思維導圖如圖2所示。圖2分層次展示了教材中一元函數微分學所包含的重要知識點，有助于學生系統地、綜合地掌握各個知識點，提高學習效率。

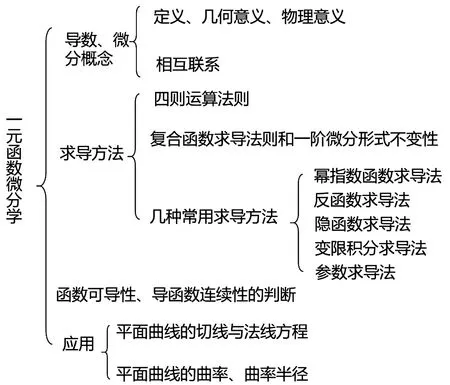
圖2 一元函數微分學思維導圖

2.4 注重理論與實際相結合

高等數學雖然抽象性較強，但其來源于實際問題，是對實際問題探索的成果。因此，在高等數學教學過程中，教師應重視抽象理論知識在實際問題中的應用，培養學生解決實際問題的能力，拓展學生的數學思維[4]。除了進行理論知識地講授，教師可適當探討其與實際生活的聯系，介紹知識點在實際問題中的應用。例如，利用常微分方程建立傳染病模型，對傳染病的傳播情況進行預測。SIS(Susceptible-Infective-Susceptible Model)模型是經典的傳染病模型之一，該模型考慮感染者恢復后可能會出現反復感染的情況，如日常感冒、發燒等。設t時刻，S(t)為易感染者，I(t)為感染者，N(t)為總人口，β為傳染率，r表示在單位時間內感染者接觸到的易感者人數，γ表示感染者康復的概率，則SIS模型可表示為

初始條件S(0)=S0,I(0)=I0。通過求解方程，對傳染病的傳播行為進行預測，以指導對傳染病的預防和控制，如通過建立華支睪吸蟲病SIS模型，研究預防性化療措施對疾病控制的長期效果[5]。將理論知識與實際應用相結合，一方面使學生認識到數學在實際生活中的應用性，激發學習數學知識的動力，另一方面能夠拓展學生的數學思維，提升數學素養。

3 結語

在高等數學教學過程中，教師應充分認識到學科的重要性，培養學生的數學素養，為學生的專業發展夯實基礎。在闡述高等數學教學現狀的基礎上，從引入數學史、問題驅動教學模式、利用思維導圖及理論與實際相結合等方面探討了優化高等數學教學效果的策略，有效提升了教學質量和教學效果。