盾構機姿態調整算法及仿真研究

薛永健

摘要：針對工程用的盾構機械在掘進的過程中的姿態問題，在分析傳統掘進姿態調整問題的基礎上，提出一種基于BP的專家控制方法。在該方法中，首先提出盾構機掘進的運動學模型，從而分析盾構機掘進的原理;其次構建基于BP+專家系統的控制方法，通過BP神經網絡的學習能力為專家系統提供實例，而通過專家系統的實例，直接對盾構機姿態進行控制。最后，通過仿真驗證了上述方法的可行性，為工程用盾構機掘進提供了實踐參考。

關鍵詞：盾構機;BP神經網絡;專家系統;姿態控制

中圖分類號：U455.3⁺9 文獻標識碼：A 文章編號：1001-5922（2021）02-0192-04

在隧道挖掘等大型地下工程中經常要用到盾構機。現階段隧道工程中，土壓平衡盾構機是使用率最高、使用范圍最廣的機械，其前端加裝的密封土艙具有穩定的切削面，在不斷向前掘進的過程中，刀盤不斷切削土體，液壓缸同步推進，機身沿著預定軌跡向前掘進。可見，在土壓平衡盾構機的掘進過程中，要想實現掘進軌跡與隧道設計軸線保持一致，就必須做好盾構機姿態的精確預測及控制。本研究則在分析盾構機姿態影響因素的基礎上，嘗試構建一個基于神經網絡的姿態調整算法，通過姿態的預測修正盾構機運行的方向，從而提高盾構機掘進的精度。

1問題的提出

盾構機在掘進時，地層條件相對均勻，且盾構機會采取直線掘進的方式進行施工。由于地層條件變化不大，因此盾構機在作業過程中承受的由地層造成的載荷是相對穩定的。可由于盾構機自身結構特征，在重力作用下容易出現“低頭”趨勢。此外，由于盾構機自身因素的影響，包括其左右受力不均，以及外殼的摩擦力矩與刀盤轉矩不平衡等，很容易造成盾構機姿態參數發生規律性變化。為解決該問題，傳統的做法是在工作狀態下通過全站儀實時檢測偏航角和俯仰角，并將檢測結果反饋給控制系統。控制系統通過調節推進液壓缸的壓力，實現盾構機的姿態糾偏。同時盾構機為實現滾轉角的有效糾偏，在每次掘進施工后，每次拼裝管片前，都必須執行反轉刀盤這一操作。可基于控制系統的糾偏方式時效性差，而手動調節容易誘發局部受力過大的問題。如何借助現有的智能算法對盾構機的姿態進行糾偏和調整，對化解盾構機掘進過程難題具有積極作用。結合以上問題，筆者認為在結合盾構機負載模型的基礎上，引人神經網絡在學習能力方面的優勢，構建一個基于神經網絡的專家控制系統，從而實時修正盾構機掘進方向。

2盾構機負載模型構建

在盾構機工作中，要保障盾構機按照設計的軸線運行，就需要分析盾構機在掘進過程中的可能受力問題。而研究認為，盾構機在掘進中與自身的結構、地質條件等有很大的關系，包括自身重力（F1）、盾尾作用力（F2）、盾尾千斤頂作用力（F3）、正面土體阻力（F4）、盾構機周圍土體作用力（F5）、后接臺車牽引阻力（F6）等作用。根據動量定理，得到：

3神經網絡的專家系統構建

3.1構建思路

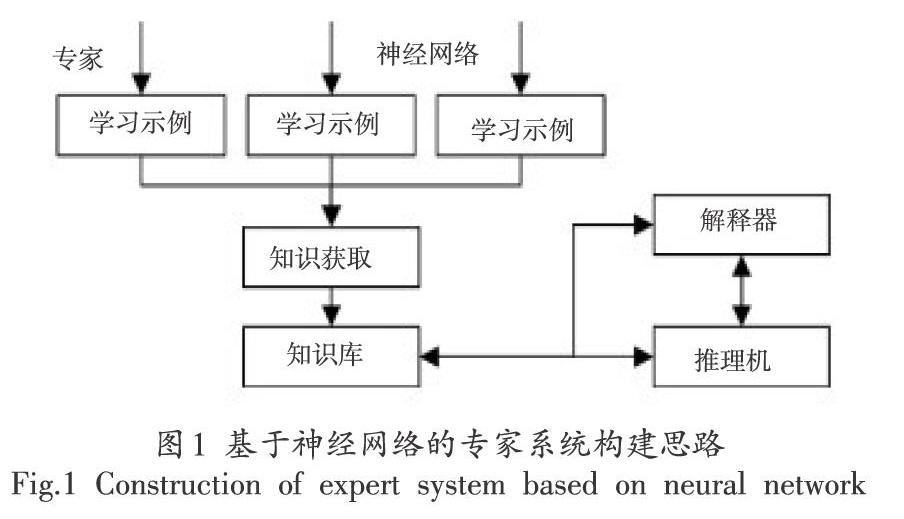
在專家系統的構建中，充分利用專家系統和神經網絡的優勢。其中通過神經網絡的學習能力構建實例，而專家系統則利用實例，為盾構機參數的調節提供基礎。具體用圖1表示。在這個過程中，神經網絡專家系統存儲掘進施工過程中的設備狀態信息和地層條件數據，從而對盾構機在當前地層條件下的姿態進行預測。如果盾構機掘進的地層條件有所改變，只需要把新的地層條件數據輸入系統，即可快速確定盾構機在新的地層參數下的應有姿態。

3.2神經網絡設計

3.2.1網絡層數的選擇

從理論上來說，神經網絡能夠逼近任何有理函數，該網絡包含線性輸出層、線性隱含層以及偏差等部分。單隱層的網絡可以對閉區間內所有的連續函數進行逼近，由此推進，基于3層網絡能夠實現各種形式的維到維的映射。一般來說，要想提高精度、減小誤差，可行的辦法有兩個，一是增加層數，二是增加隱藏層中神經元的數量。由于增加層數會導致原本復雜的網絡更加復雜，進而使網絡權值的訓練時間更長，降低工作效率，故一般不采用增加層數的方法。所以，提高隱含層中的神經元數量就成為了提高精度的優選辦法。基于此，本文建立3層神經網絡。

3.2.2層數設計

輸入層的主要用途是輸入各類已接收的數據信息，輸出層的主要作用是輸出經過處理后的最終結果。一般來說，輸人層和輸出層的設計主要關聯于應用問題的具體情況，應用問題的輸入數決定了神經網絡的輸入個數，應用問題的輸出數目決定了輸出層的神經元個數。

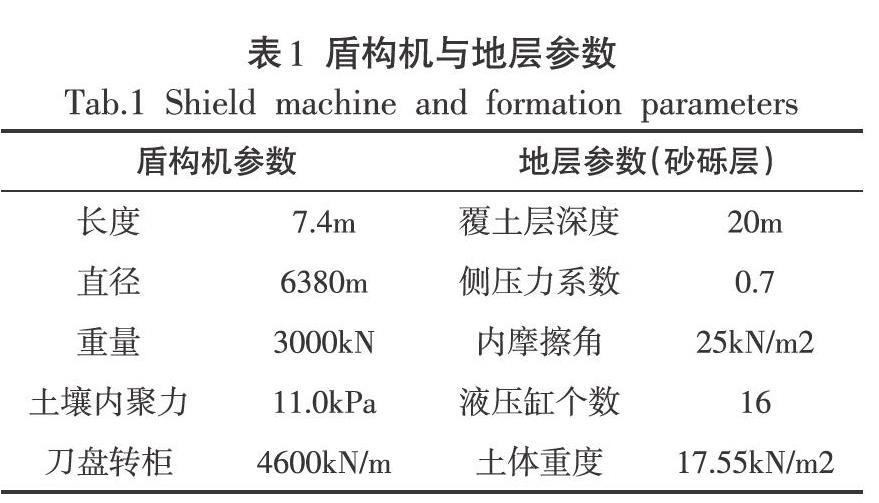
輸入層的輸入參數主要如表1所示。

輸出層提供最終的處理結果，主要是滾轉角、俯仰角和偏航角。

基于地層條件參數，根據盾構機在進行挖掘工作時的受力分布情況，本文設定輸入層有13個神經元，并設定輸出層的神經元數量是3個。

在進行數據處理之前，為提高網絡訓練的效率，本文首先對神經網絡的輸入、輸出數據進行了預處理。通過比較Matlab內置主成分分析、標準化處理以及歸一化處理等多種方法，在權衡以后，本文最終選定了歸一化處理法對數據進行預處理。

“歸一化”指的是把擁有多個尺度、分屬不同區間的樣本矢量的各個分量劃人相應的區間內，由此，可以利用統一尺度對樣本的各個分量進行表征。目前，在神經網絡的訓練中經常應用到歸一化處理法，在實踐中發揮出重要的應用價值。若輸入值在[-1，1]區間外，sigmoid函數的輸出響應對輸入的敏感性較低。而對輸入數據執行歸一化處理以后，可以確保數值較大的輸入能夠分布在sigmoid函數梯度較大的區間內。為了避免在調節權重時造成振蕩或超調等問題，輸入向量的各個分量最好能夠處于同一數量級，而且變化范圍適中。在實操中，并未嚴格要求換算關系，原則上只要能夠轉換為區間[0，1]內的值，即可達成網絡訓練效果，而且不易出現分散的結果。

其中，x表示初始數據，x表示經過預處理后的數據;MinValue表示最小的初始樣本值，MaxValue表示最大的初始樣本值。

在本研究中，選用掘進施工中的第100～119環的20環姿態參數作為樣本，并從每一環中選出10個測量點共200個測量點。通過分析這200組數據，得到俯仰角的最大值5.8和最小值0.1，偏航角的最大值5.173'和最小值0.568，滾轉角的最大值1.231'和最小值0.097'。為了節省篇幅，以下僅展示了第100環的姿態角數據及其歸一化處理后的結果。

前文已述，本文神經網絡的輸入層、輸出層的神經元數量依次是13個和3個，結合以上列出的三個參考公式，針對現實狀況，可以估計本文神經網絡中隱含層的神經元數量取自于5～15。所以，設定隱含層節點數h的值為5-15的自然數。最佳隱含層神經數量的確定需要不斷通過試驗檢測，在本研究中，隱含層神經元數量為7時，達到了最佳狀態。因此，本研究設定隱含層的神經元數量為7。

4預測結果與分析

4.1預測結果

選用第100～119環共20環的姿態參數作為樣本，通過網絡訓練可以得到訓練的參數，并在訓練結束后建立神經網絡模型，并通過該模型對3個姿態角進行預測，所得預測結果依次展示于下圖（2）～圖（4）：

以上圖中的實線表示BP神經網絡的預測結果，圓點表示實測數據。上圖中僅展示了前5環的姿態參數，但是仍然可以窺探出姿態參數的變化規律。

4.2誤差分析

根據上述的預測結果，與實際的掘進位置進行比較，得到表4所示的誤差分析結果。

根據上表4看出，最大誤差是0.0209，如果盾構機在此條件下進行工資，那么直線掘進1000m將會出現5.8mm的位置偏差，說明訓練以后的神經網絡模型能夠較為精準地預測盾構姿態參數。

同時從上述的結果看出，在盾構機向前掘進一個襯砌管片的長度時，盾構機停止掘進，開始拼裝襯砌管片，在重啟刀盤時，受到地層瞬間作用力的影響，盾構機的滾轉角、偏航角及俯仰角瞬時激增。在繼續向前掘進的過程中，控制系統會對偏航角、俯仰角進行調節，使得這兩項姿態參數有所減小，而滾轉角是由反轉刀盤進行調節的，所以滾轉角是在該環結束以后才開始減小的。上圖清晰地展現了盾構機姿態參數在盾構掘進過程中的變化規律，也證實了訓練后的神經網絡模型可以對盾構機姿態參數進行準確預測。

5結語

神經網絡模型能夠檢驗盾構機當前的掘進施工狀態是否正常，還能對盾構機在版圖中地層條件下的姿態參數進行預測，以預測結果作為依據，操作人員可以快速做出反應，及時調整盾構機掘進姿態，降低掘進過程的偏差，最終保證隧道工程質量。