應用激光跟蹤儀的三坐標測量機幾何誤差檢測方法

韓 林，米 良*，劉興寶,3，滕 強，唐 強，夏仰球

(1.中國工程物理研究院 機械制造工藝研究所，四川 綿陽 621900；2.國家機床產品質量監督檢驗中心（四川），四川 成都 610200；3.南京理工大學 發射動力學研究所，江蘇 南京 210094)

三坐標測量機（coordinate measuring machine，CMM）由于測量精度高、效率高等優勢，廣泛應用于精密加工檢測領域。作為高精度的測量基準，幾何誤差直接影響三坐標測量機的測量精度和整機性能，尤其是納米級精度的三坐標測量機[1]。因此，三坐標測量機幾何誤差的快速、高精度檢測技術是其性能提升的關鍵，也是三坐標測量機設計制造過程中的重點研究方向。

目前，常用的機床、三坐標測量機幾何誤差檢測手段主要有高精度實物基準測量法[2]、激光干涉儀測量法[3]、球桿儀測量法[4]、R-test等測量方法[5]。但上述測量方法存在安裝調整困難、對操作者要求較高、測量耗時等缺點，且無法獲取裝備工作空間內的空間位置誤差，不能滿足幾何誤差高精度、高效率的檢測需求。激光跟蹤儀作為一種大尺寸、高精度、便攜的空間測量設備，在數控裝備和三坐標測量機精度檢測領域有廣泛的應用[6]。Schwenke等[7]利用激光跟蹤干涉儀在2 h內完成了三坐標測量機幾何誤差的快速和高精度檢測；王金棟等[8]在4 h內利用激光跟蹤儀對三軸銑床幾何誤差進行了檢測；陳洪芳等[9]優化了激光追蹤儀測量算法，對三坐標測量機空域坐標進行了補償修正；Ibaraki等[10]利用激光跟蹤儀進行了機床空間誤差檢測，并對兩種空間誤差測量方法進行了不確定度分析。

應用激光跟蹤儀進行三坐標測量機/機床幾何誤差檢測的多站測量方法常用求解過程主要包括基站自標定和測量點空間坐標標定[11–13]。上述方法存在如下局限性：1）利用4個激光跟蹤儀間的位置關系建立測量坐標系，實現基站自標定和測量點標定，需要坐標轉換到三坐標測量機/機床坐標系下求解，難以直接分離得到幾何誤差項；2）在三坐標測量機/機床坐標系下進行幾何誤差直接求解時，需要通過理論目標點來實現基站自標定，在精度較差的三坐標測量機檢測過程中容易引入較大的自標定誤差，限制了激光跟蹤儀的使用范圍。

針對上述問題，作者提出了一種基于幾何誤差約束條件在三坐標測量機坐標系下直接求解幾何誤差的方法。首先，結合多體系統理論和齊次坐標變換方法建立三坐標測量機幾何誤差模型；其次，建立應用激光跟蹤儀的幾何誤差檢測數學模型，結合幾何誤差自身約束條件和Levenberg–Marquardt方法實現在三坐標測量機坐標系下幾何誤差的直接求解，進而實現空間位置誤差預測；最后，利用激光干涉儀進行單項定位誤差和體對角線空間誤差檢測對比驗證試驗。

1 三坐標測量機幾何誤差建模

假定三坐標測量機各軸線為理想剛體，在運動過程中存在3項位置偏差和3項姿態偏差。因此，三坐標測量機共存在21項幾何誤差，包括3軸18項位置和姿態誤差，以及3直線軸間的3項垂直度誤差。Y軸的6項幾何誤差如圖1所示，3軸間垂直度誤差如圖2所示。其中：Ehk為k軸在h方向上的線性偏差（h、k為X、Y、Z）；Exy為y軸繞x軸的角度偏差（x為A、B、C，y為X、Y、Z）；EAOZ為YZ軸間的垂直度誤差；EBOZ為XZ軸間的垂直度誤差；ECOX為XY軸間的垂直度誤差。

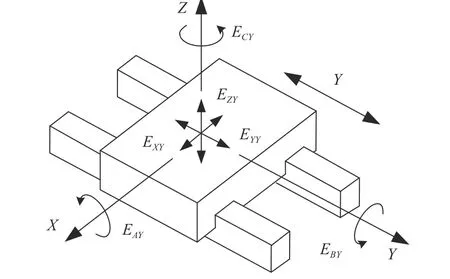
圖1 Y軸6項幾何誤差項Fig. 1 Six geometric errors of Y axis

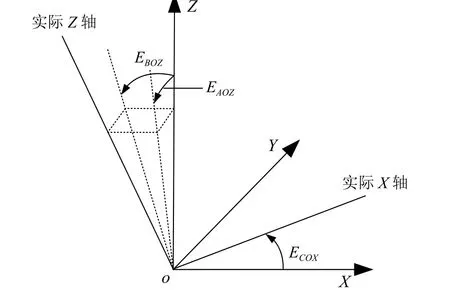
圖2 垂直度誤差分布Fig. 2 Distribution of squareness errors

假定測量點距測頭中心足夠近，可忽略在測頭坐標系下的坐標，此時在誤差建模中僅存在17項幾何誤差，即不包含ECX、EAZ、EBZ和ECZ。幾何誤差建模方法可根據多體系統理論，結合齊次坐標變換的方法，在小角度假設條件下實現，詳見文獻[14–16]。此處給出從工件到測頭運動的傳遞鏈為W工件—F床身—Y軸—X軸—Z軸—T測頭的三坐標測量機的幾何誤差模型，如式（1）所示。

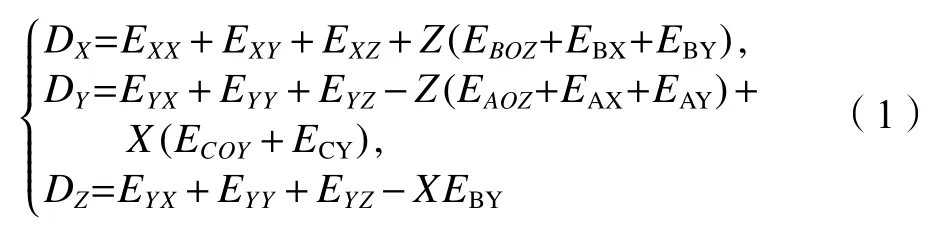
式中，DX、DY、DZ代表測頭中心在X、Y、Z方向的空間位置誤差，X、Y、Z表示三坐標測量機控制各軸移動的坐標指令。

式（1）可以表述為式（2）的矩陣形式：

設定總體空間位置誤差DV為X、Y、Z方向誤差的平方和開根，如式（3）所示。

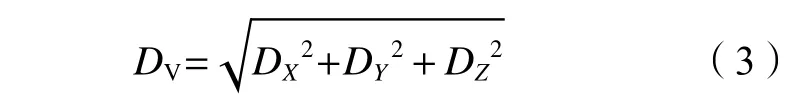
分離得到各項幾何誤差后，可建立各項幾何誤差與各軸位置之間的關系，通過線性插值的方法，利用式（1）預測全域內空間位置誤差分布。因此，式（1）既是幾何誤差分離模型的重要組成部分，又是三坐標測量機工作空間內空間位置誤差的預測模型。

2 跟蹤儀幾何誤差測量與分離原理

將激光跟蹤儀分別放置在三坐標測量機工作臺的若干個位置，控制三坐標測量機移動到空間中若干個點進行測量，應用激光跟蹤儀檢測幾何誤差的原理如圖3所示。

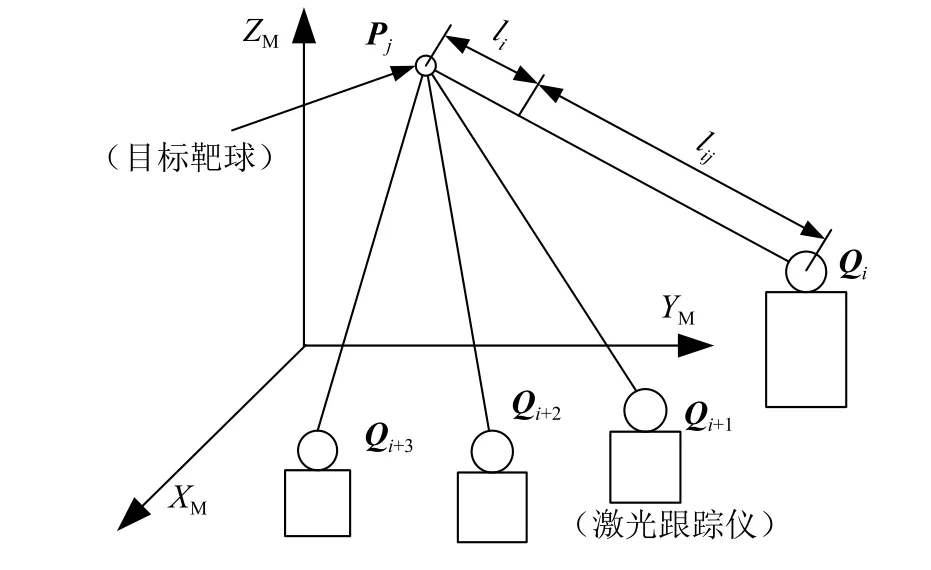
圖3 激光跟蹤儀檢測基本原理Fig. 3 Measurement principle of laser tracer

在三坐標測量機坐標系XMYMZM下，假定空間中有m個激光跟蹤儀站位分別對n個測量點進行跟蹤測量，根據兩點間距離公式，可以將第i個跟蹤儀對第j個測量點的測量過程表達為：

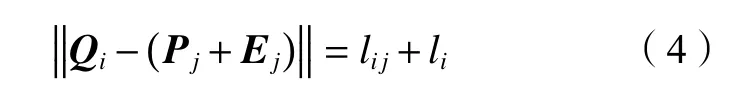
式中：Qi為第i個激光跟蹤儀的空間位置坐標矢量；Pj為第j個測量點的位置坐標矢量；Ej為第j個測量點的空間位置誤差矢量，可由式（2）計算得到；lij為第i個激光跟蹤儀與第j個測量點間的距離讀數；li為死區長度，對于絕對測距激光跟蹤儀此項為0。

整個測量過程可描述為對式（5）進行最優化求解。

為實現式（5）的求解，利用泰勒1階線性展開后可得到：

式中：J為非線性方程組的雅可比矩陣；d為方程中的未知量，包括激光跟蹤儀的坐標位置、三坐標測量機的17項幾何誤差及死區長度；Fd為方程組線性化后常量矩陣。

此類問題求解屬于秩虧自由網平差求解范疇，秩虧為6，需要施加約束條件才能求解。因此，利用幾何誤差特性進行約束，實現在三坐標測量機坐標系下幾何誤差的直接求解，約束條件為三坐標測量機各坐標軸原點處的幾何誤差均為0，在各軸遠端處的直線度誤差為0，可用式（7）表達：

式中，B為僅在約束幾何誤差項所對應的矩陣對角線值為1、其余值均為0的系數矩陣。

結合式（6）和（7）可以得到式（8）：

式中，M=[J B]T，G=[Fd0]T。

式（8）可以通過最優化迭代算法進行求解，如Levenberg–Marquardt方法，該方法每次迭代步驟如式（9）所示。

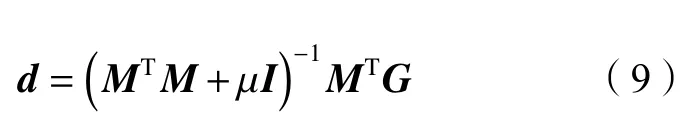
式中，μ為松弛因子，I為單位矩陣。

為保證式（9）方程組存在解和求解冗余性，在實際測量過程中設定激光跟蹤儀站位數m=4；而且激光跟蹤儀4個測量位置坐標不共面，測量點遍布整個測量空間，每個位置處的測量軌跡可不相同。

3 試驗驗證

3.1 激光跟蹤儀幾何誤差檢測試驗

在（20.0±0.5） ℃標準溫度環境下，對FYXZ型式的三坐標測量機進行幾何誤差檢測。三坐標測量機測量過程中，設定參數如表1所示。

表1 三坐標測量機試驗參數Tab. 1 Experimental parameters of CMM

此外，激光跟蹤儀依次放置在工作臺上的4個位置（LT1、LT2、LT3和LT4），目標靶球（R）放置在Z軸端部進行檢測，測量過程中應保證不發生斷光，如圖4所示。激光跟蹤儀在4個位置處的檢測軌跡相同，均為三坐標測量機測量空間形成的長方體的12條棱邊。

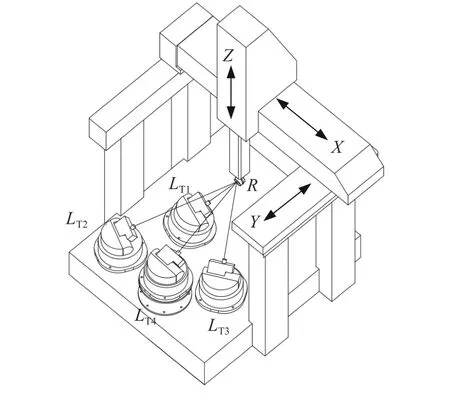
圖4 激光跟蹤儀檢測幾何誤差示意圖Fig. 4 Schematic diagram of geometric error measurement of CMM using laser tracer

三坐標測量機幾何誤差檢測結果如表2所示。表2中：X、Y、Z軸幾何誤差均為檢測結果的最大值與最小值之差，負號表示幾何誤差與X、Y、Z軸正方向相反；垂直度誤差負號表示兩軸間夾角小于90°。X、Y、Z軸定位誤差和XY軸間垂直度誤差較大，可認為是此三坐標測量機的主要誤差來源。

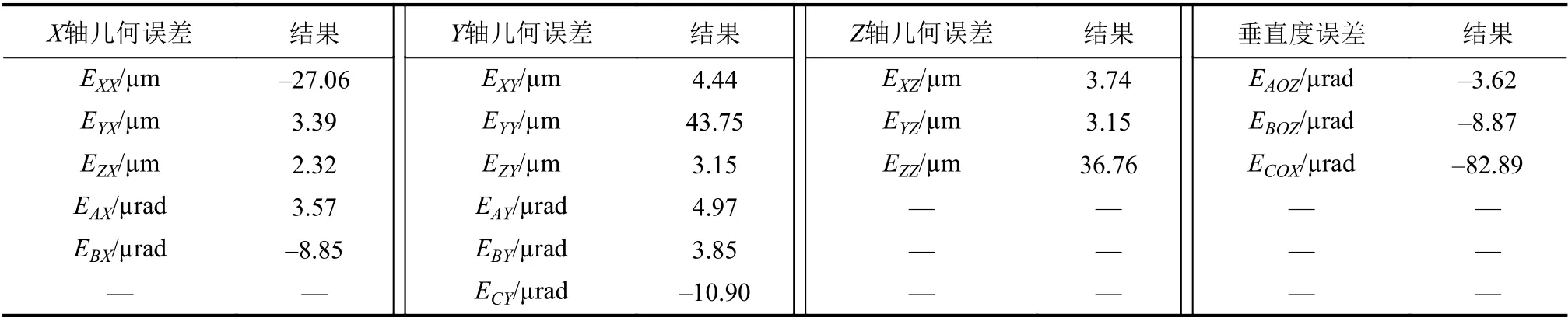
表2 三坐標測量機17項幾何誤差檢測結果Tab. 2 17 geometric error measurement results of CMM

利用計算得到的17項幾何誤差，結合幾何誤差模型和線性插值方法可以預測測量空間內任一點的空間位置誤差，進而利用式（3）可以得到三坐標測量機每個空間位置點的總體空間位置誤差。在工作空間內的總體空間位置誤差預測分布如圖5所示。程中應當盡量避免極限區域，也應當利用空間位置誤差補償方法實現三坐標測量機精度的提升。

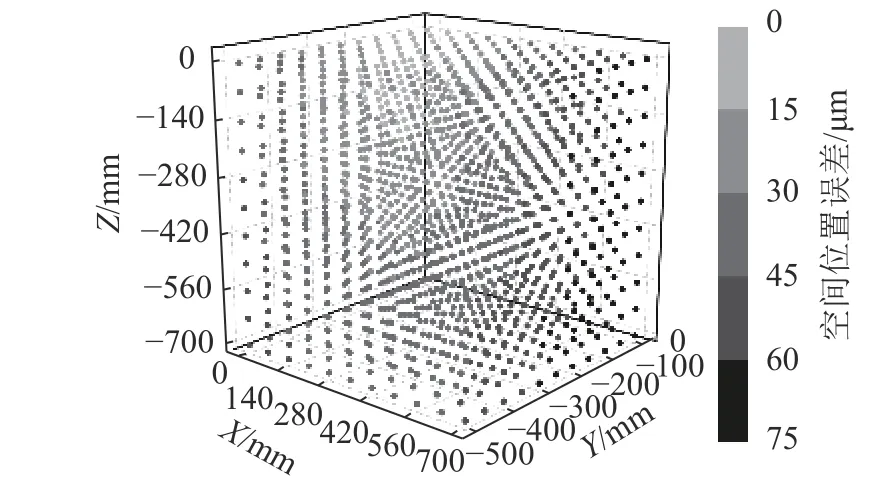
圖5 三坐標測量機空間位置誤差預測分布Fig. 5 Volumetric error distribution of coordinate measuring machine

3.2 單項幾何誤差對比試驗驗證

為了驗證激光跟蹤儀檢測和分離得到的幾何誤差的正確性，在相同環境下利用雷尼紹XL–80激光干涉儀進行XYZ軸定位精度的檢測。激光干涉儀檢測位置與跟蹤儀檢測部分軌跡重合。檢測現場如圖6所示，激光干涉儀檢測過程中相關參數如表3所示。

從圖5可得，三坐標測量機總體空間位置誤差最大為74.64 μm，而且在測量空間極限遠端位置區域的空間位置誤差較大，尤其是右下角區域。后期使用過

激光干涉儀檢測結果為往復5次結果求取平均。激光干涉儀與激光跟蹤儀測量的各軸定位誤差檢測結果如圖7～9所示。

從圖7～9中可以得到：激光跟蹤儀檢測和分離得到的Z軸單項誤差與激光干涉儀檢測結果趨勢和幅值均相近；X軸定位偏差相差4.15 μm，Y軸定位偏差相差7.43 μm，Z軸定位偏差相差5.93 μm。兩者之間的差異是由于激光跟蹤儀通過測量空間軌跡分離得到幾何誤差，而激光干涉儀是測量單條直線所得到的綜合測量結果。但是兩者總體相近，可以驗證該方法的正確性。

圖6 激光干涉儀檢測定位誤差Fig. 6 Positioning error measurement using laser interferometer

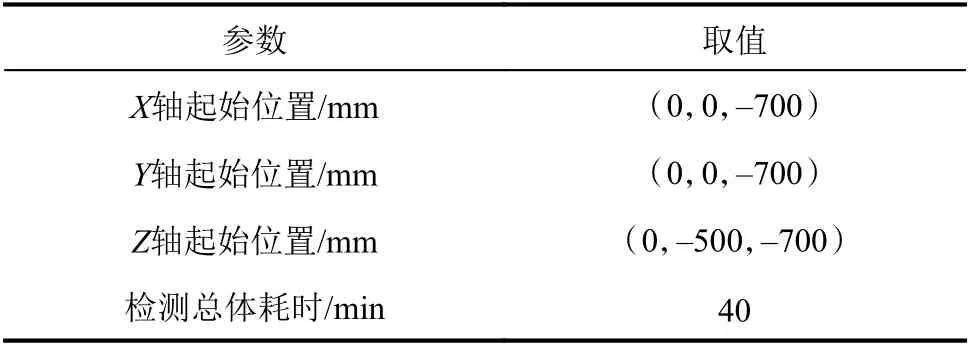
表3 激光干涉儀試驗參數Tab. 3 Experimental parameters of laser interferometer

圖7 X軸定位誤差對比Fig. 7 Comparison of positioning error of X axis

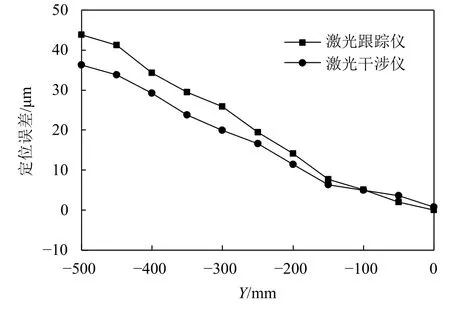
圖8 Y軸定位誤差對比Fig. 8 Comparison of positioning error of Y axis

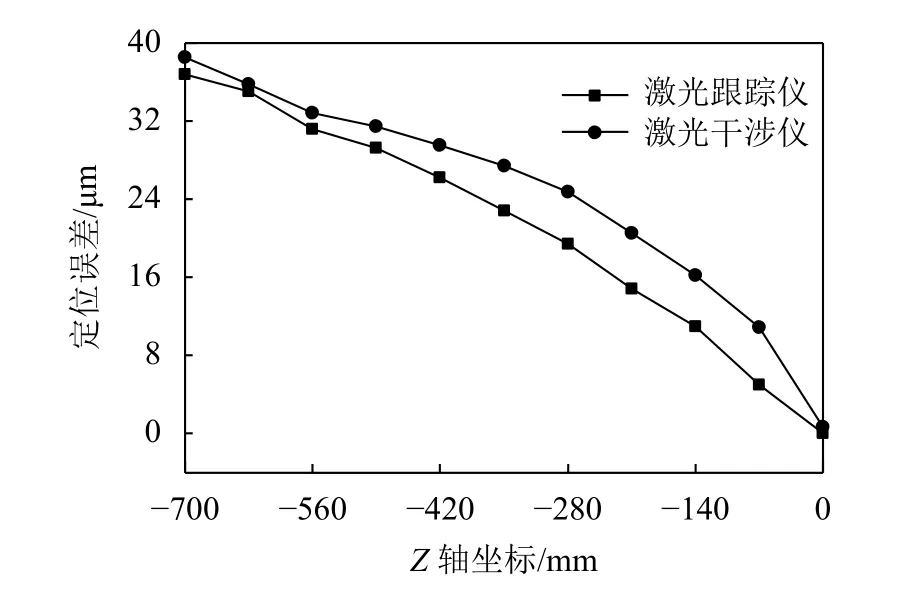
圖9 Z軸定位誤差對比Fig. 9 Comparison of positioning error of Z axis

3.3 空間位置誤差對比試驗驗證

空間誤差是評價三坐標測量機性能的關鍵因素，也是三坐標測量機精度提升的關鍵。因此，在相同檢測條件下，利用本文所提方法與文獻[11,13]所提空間誤差檢測方法，均使用Levenberg–Marquardt方法處理得到實測軌跡的空間誤差與激光干涉儀檢測結果進行對比。激光跟蹤儀與激光干涉儀檢測軌跡與第3.2節中相同，X軸和Y軸空間誤差計算結果如圖10所示。

圖10 不同分離方法的空間誤差對比結果Fig. 10 Volumetric error comparison results of different measurement methods

從圖10中可以得到：文獻[11]方法檢測結果與激光干涉儀檢測結果相比，X最大相差11.14 μm，Y軸最大相差3.21 μm，可能與激光跟蹤儀的布局和測量點的空間分布有關；文獻[13]方法整體與激光干涉儀檢測結果相差較大，X軸最大相差45.5 μm，Y軸最大相差16.61 μm，由于三坐標測量機精度較差，在自標定過程中引入了較大的自標定誤差；本文方法與激光干涉儀檢測結果相比，X軸最大相差2.8 μm，Y軸最大相差5.3 μm。綜上，在相同條件下，本文方法避免了激光跟蹤儀的自標定，能夠較為準確地反映三坐標測量機空間位置誤差的分布。

為驗證利用幾何誤差模型預測得到的空間位置誤差的正確性，根據三坐標測量機生產制造過程中進行精度檢測調整常用的4條體對角線定位誤差，進行激光跟蹤儀預測值與激光干涉儀實測值的對比試驗。三坐標測量機4條體對角線設定見表4。PPP體對角線定位誤差檢測現場如圖11所示，體對角線檢測試驗總體耗時2 h。

表4 體對角線位置設定Tab. 4 Position setting of body diagonals

圖11 激光干涉儀檢測PPP體對角線定位誤差現場Fig. 11 Positioning error measurement of PPP body diagonal using laser interferometer

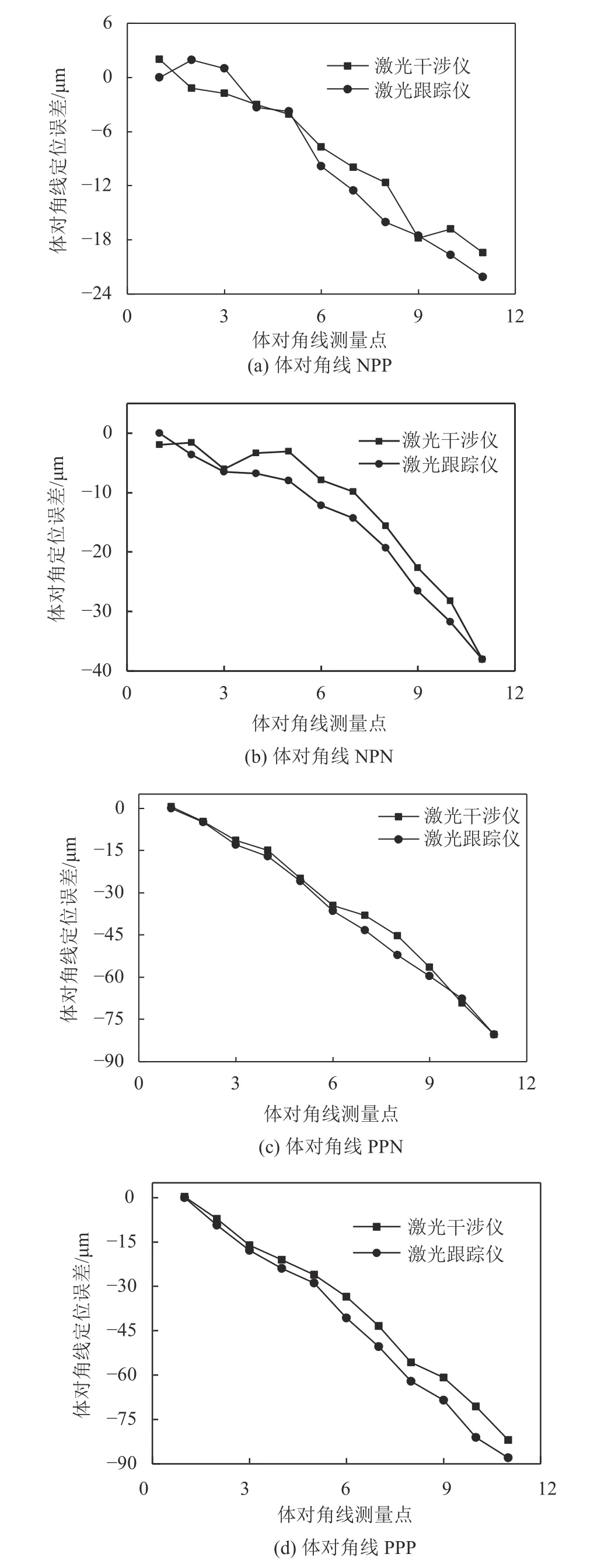
圖12 體對角線預測與實測空間位置誤差對比Fig. 12 Volumetric positioning error comparison of measured and predicted values of body diagonals

將激光干涉儀在每個三坐標測量機位置往復5次的測量結果求取平均作為實測值。利用激光干涉儀進行檢測的體對角線定位誤差與激光跟蹤儀預測值進行對比，結果如圖12所示。

從圖12中可以得到，激光跟蹤儀預測與激光干涉儀實測體對角線定位誤差趨勢相近，且誤差值總體較為接近。其中，預測與實測值中NPP定位誤差最大相差4.42 μm，NPN定位誤差最大相差4.89 μm，PPN定位誤差最大相差6.77 μm，PPP定位誤差值最大相差10.51 μm，可以說明空間位置誤差預測模型的正確性。激光跟蹤儀通過部分軌跡檢測可以預測工作空間內所有位置的空間位置誤差，便于通過誤差補償方式實現三坐標測量機精度的提升。此外，激光跟蹤儀檢測速度快、效率高，較傳統測量方法有更大的優越性。

4 結 論

1）建立了三坐標測量機的幾何誤差模型和激光跟蹤儀檢測原理模型，并利用幾何誤差約束條件，實現了幾何誤差的直接分離。該方法不需要進行激光跟蹤儀位置的自標定，簡化了求解步驟，提高了幾何誤差測量精度。

2）在某三坐標測量機上進行了幾何誤差檢測試驗和空間誤差預測。與激光干涉儀檢測結果相比，三軸定位誤差最大相差7.43 μm，體對角線定位誤差最大相差10.51 μm，驗證了幾何誤差分離方法和空間位置誤差預測模型的正確性。該方法與常用的激光跟蹤儀檢測幾何誤差方法相比有較大優勢，能夠更為準確地反映空間誤差分布。三坐標測量機預測空間誤差最大值為74.64 μm，且位于測量空間極限區域位置。

3）應用激光跟蹤儀的三坐標測量機幾何誤差檢測總耗時2 h，比傳統的激光干涉儀對X軸、Y軸和Z軸定位精度和4條體對角線位置精度的檢測效率高；而且便于三坐標測量機空間位置誤差補償，在三坐標測量機和數控機床精度檢測領域有較大的應用空間。