脈動橫風對高速列車平穩運行的影響

杜家俊，吳一塵，關海寧

（長安大學 工程機械學院，西安 710064）

中國的高速鐵路里程仍在不斷增長，建設布局從中東部逐漸轉移至西部，西南及西北地區的高鐵建設正處于攻堅克難階段，西南的高山深谷、西北的大漠風區，這些殘酷的自然環境使高速列車運行面臨著諸多挑戰［1-2］。高速列車尤其是長大編組形式進入風環境（如橋隧相連區段往往深處高山深谷，峽谷風明顯），突然遭遇橫風激擾，空氣流動帶來阻力、升力、扭轉力矩會極大地影響列車運行狀態，如車輛偏載、橫向平穩性急劇惡化、輪軌接觸狀態變差，甚至強風下出現脫軌、傾覆等情況，不但直接影響乘坐舒適性，甚至危及行車安全，所以橫風下的列車運行平穩性、安全性問題不容忽略。

目前國內外許多學者對于風環境下車輛運行問題有一定討論。Carsten Proppe等［2］研究了非穩態橫風下車輛穩定性，其標準陣風與脈動風速結合的風載模型是一大特點。于夢閣等［3-4］研究了列車在強側風下的安全行駛問題，并進一步分析了橋梁上運行的高速列車側風安全性。張云飛等［5-7］針對山區城市地鐵列車行駛于高架線路跨越江河時遭遇橫風的情況進行了初步探究。郗艷紅等［8-9］利用計算流體力學（CFD）方法對橫風作用下列車安全速度限值進行了分析。

目前文獻中對于完整長大編組列車的研究較少（多為1輛頭車或3輛編組），計算方法多為CFD導致計算速度過慢（大渦模擬對外形精度、網格質量過高），或者風洞試驗方法（成本高、實施困難）。針對這些，將利用在列車動力學模型加載橫風激勵的方法，研究長大編組列車的橫風平穩性問題。結合列車多剛體動力學模型、空間脈動風場載荷激勵模型的計算模型，進行大長編組高速列車在脈動風場中的運行平穩性分析，探究脈動橫風下的列車運行基本特性及該條件下的車速與風速安全限值，以此來為高速列車初期設計階段的性能評價和參數優化提供新思路和快速低成本的模擬方法。

1 高速列車動力學模型

本文所用高速列車精細模型基于多體動力學計算軟件UM進行搭建，如圖1所示。列車模型選用CRH3型高速列車，按照4動4拖形式進行編組，具體形式為［T1+M2+M3+T4+T5+M6+M7+T8］，由于每輛車間橫向、垂向自由度為弱耦合，而橫風作用主要為橫向力作用，故列車模型中弱化了車鉤。車輛簡化為1個車身、2個轉向架及4個輪對組成，7個部件均為剛體，每個剛體有橫移、浮沉2個平動以及側滾、點頭和搖頭3個轉動，整車共35個自由度，整列車為280個自由度［4，7，9］。每輛車具體的自由度設置情況如表1所示。

表1 高鐵車輛自由度設置情況

而車輛內部分層彈簧-阻尼系統中，懸掛系統均為黏性阻尼（垂向液壓裝置均考慮了非線性特性），彈簧考慮為線性模型，另外二系懸掛采用空氣彈簧（考慮為線性彈簧），同時考慮了抗蛇行減振器、垂/橫向減振及橫向止擋等部件（均考慮非線性特性）；并允許輪軌相互脫離，輪軌之間為非線性彈性接觸，并選用相應的非線性接觸處理算法計算［3，7-8］。車輛的動力學參數見表2。

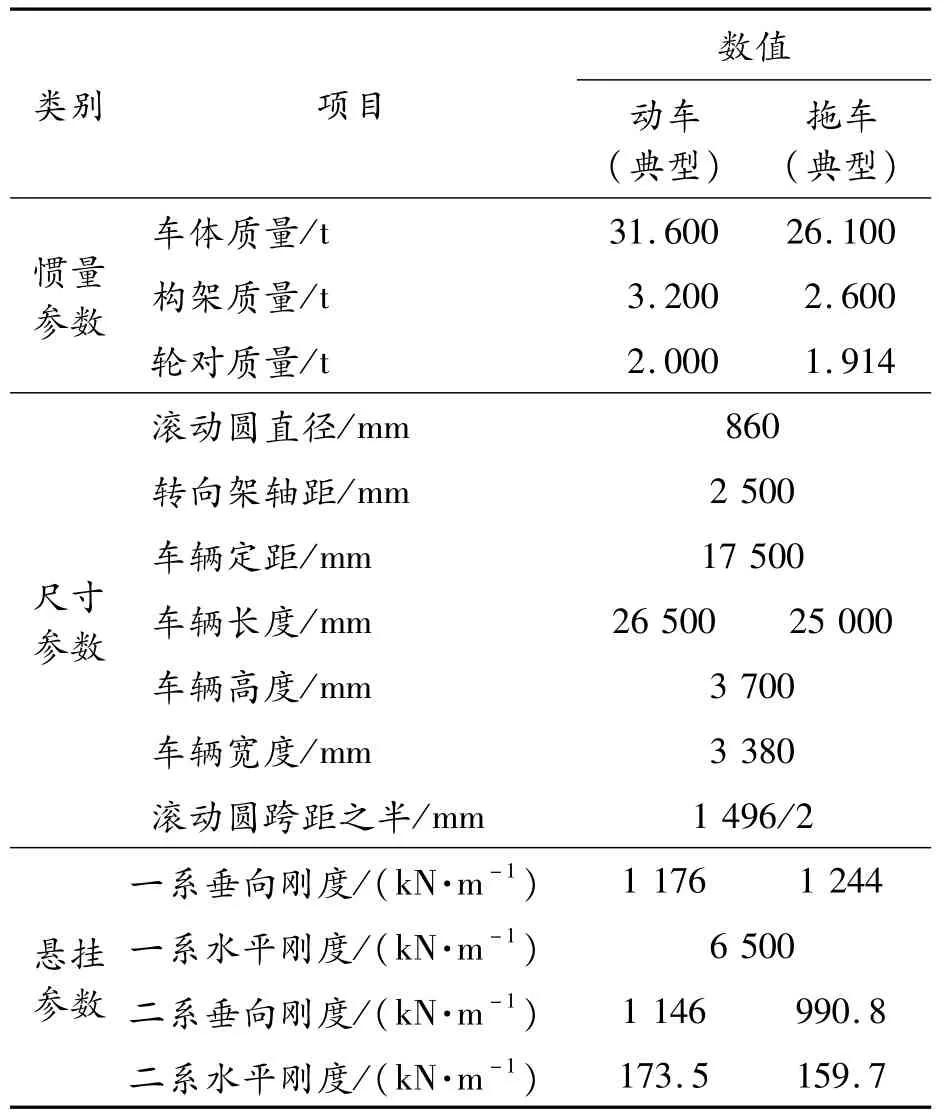
表2 某高速動車組基本動力學參數

由于脈動橫風激勵主要范圍為在7 Hz以內，在此列出車輛的低階模態信息，見表3。

基于此，則橫風激擾下的高速列車車輛的動力學方程可描述為：

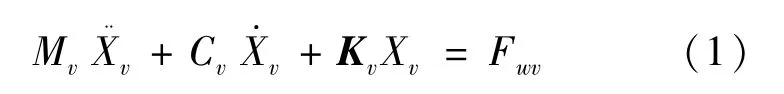
式中：“v”代表車輛；Mv、Cv及Kv分別是車輛的質量、阻尼及剛度矩陣；及Xv分別是車輛的加速度、速度、位移矢量；Fwv為車輛所受風載荷。

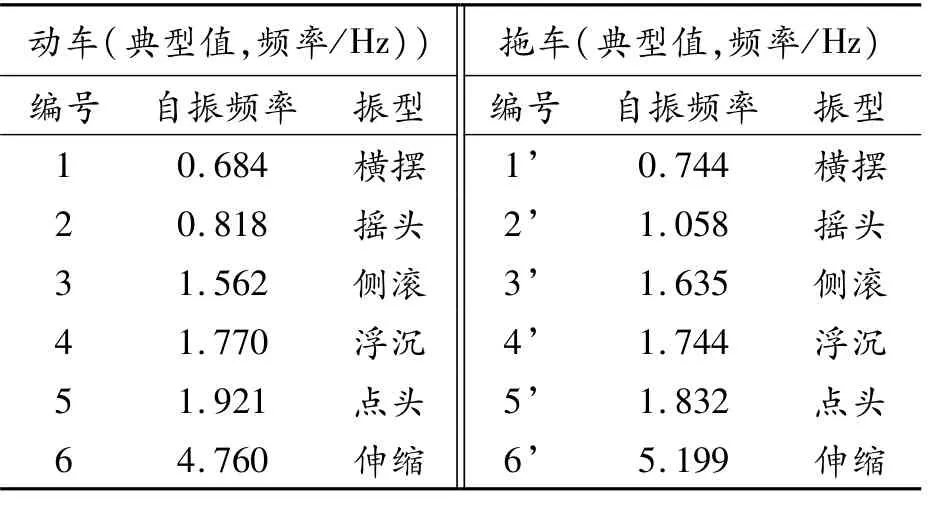
表3 列車10 Hz內低階模態

如圖1所示，鋼軌采用CN-60軌，車輪踏面為LMA型，輪軌接觸模型采用基于FASTSIM蠕滑力算法。確定鋼軌及車輪材料屬性后，可由FASTSIM算法計算輪軌接觸面的主曲率、法向力、橢圓接觸斑半軸、縱向和橫向蠕滑率與自旋的當前數值［4，7，9］。軌道隨機不平順采用某城際高速鐵路段實測不平順，時域樣本如圖2所示。

圖1 高速列車編組的多剛體動力學模型及局部展示

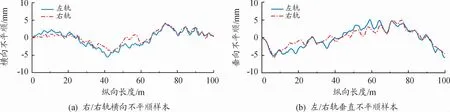
圖2 某城際高鐵軌道不平順時域激勵樣本

2 脈動風場載荷模型

2.1 脈動風速數值模擬及其驗證

Kaimal于1972年提出了沿高度變化的譜密度，其簡化形式可以表示為［10-11］：

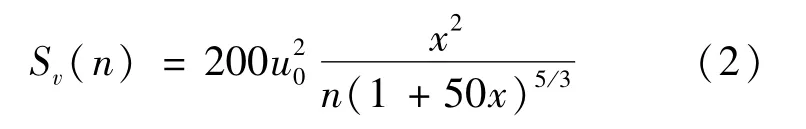
脈動風并非完全同步，與風速及各點的相對位置有關，需考慮互功率譜相干函數。任意2項i、j的風速互功率譜密度可以由下式確定：

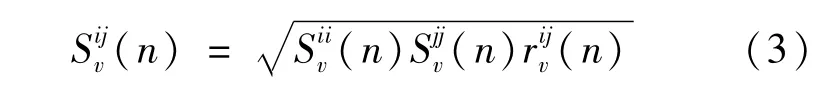
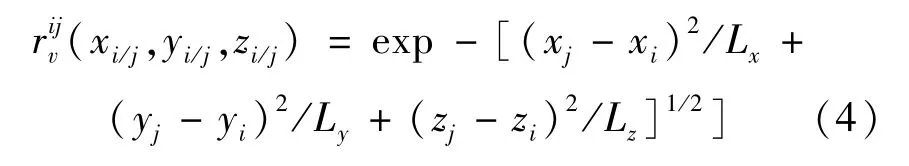
式中：x、y、z為模擬風速點的空間坐標；Lx、Ly、Lz分別為考慮風速空間各方向相關性的系數，取值為Lx=Ly=50，Lz=60。

脈動風隨機過程采用線性濾波法中的自回歸（auto-regressive，AR）模型進行程序編寫，該方法具有模擬精度高、計算速度快、占用資源少等優點，在Matlab中易實現［10-11］。平均風速為12 m/s時的脈動風空間模擬加載點時域樣本見圖3（a）及圖3（b），相應目標譜與計算譜見圖3（c）與圖3（d）。

圖3中光滑曲線為目標譜功率譜曲線，粗糙有毛刺的曲線表示用線性濾波法所得到的脈動風速時程計算譜曲線。通過對比可知，2個典型位置（頭車T1及尾車T8處）時域風速呈現出不同脈動過程，而仿真得到的模擬譜線基本上圍繞在目標譜兩側浮動，計算譜與目標譜規律性一致、數值吻合程度好，可證明AR方法模擬脈動橫風是有效的。

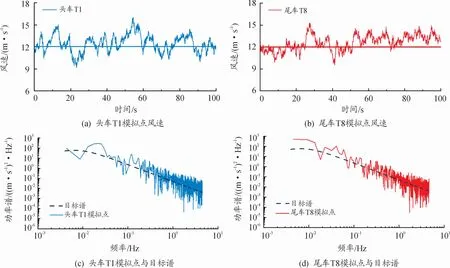
圖3 脈動風速數值模擬及其驗證

2.2 列車氣動載荷模型

當車輛以勻速Uv運行時，車輛受到攻角α的自然風Uw。由速度的矢量合成可以計算出車速、風速和風向角的合成風速UR、合成風向角β［7，12-14］。詳情如圖4所示。

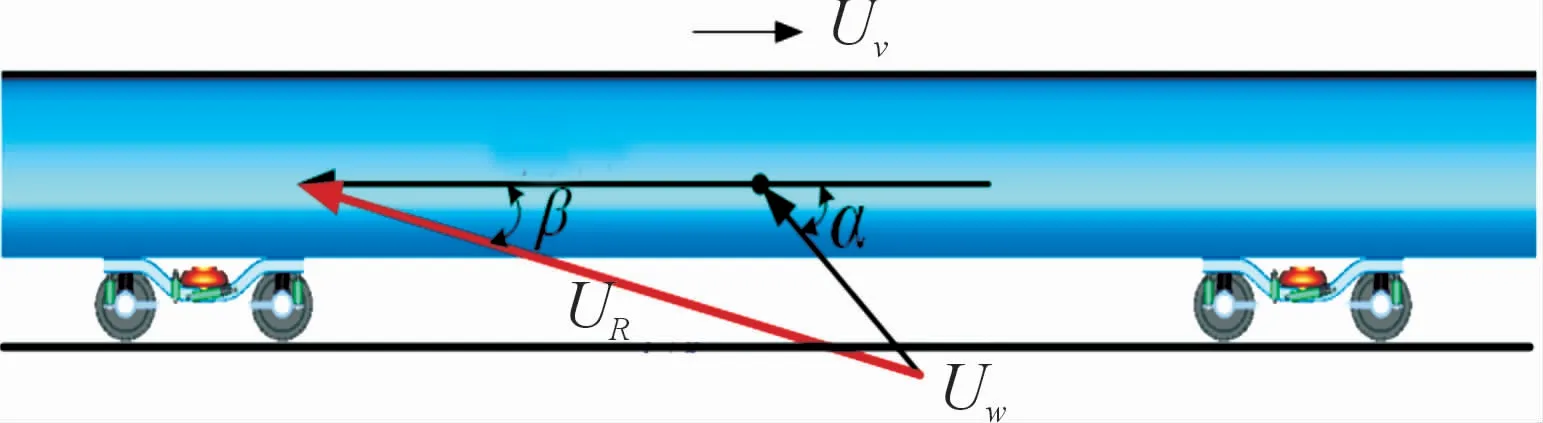
圖4 風速與車速矢量圖

則橫風與車輛移動合成的相對速度Ur及偏航角β可描述為：

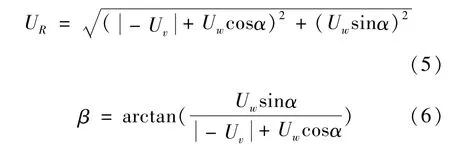
橫風激擾下，作用于高鐵車輛的橫風力系主要由阻力Dv、升力Lv及扭轉力矩Mv組成。則作用于移動車輛車體上的橫風載荷力系為：

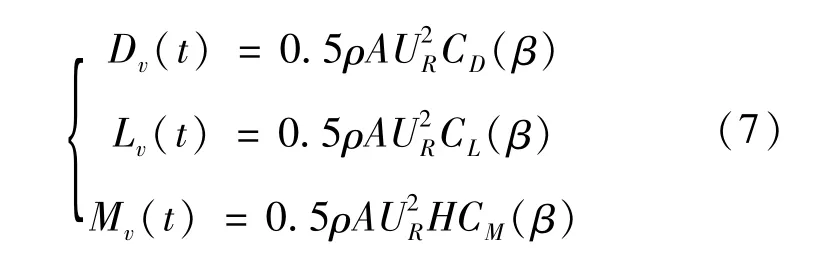
計算車輛風載荷時使用定常系數法，風攻角90°時車輛氣動載荷系數如表4所示［7］。

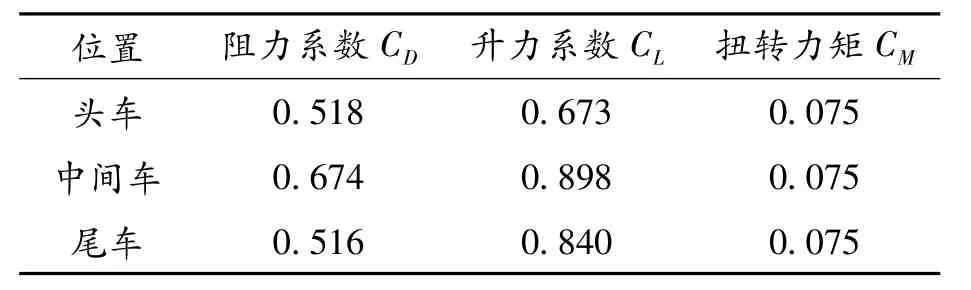
表4 車輛氣動三分力系數

3 脈動橫風下列車運行基本特性

3.1 加載脈動橫風對車輛振動的影響

列車突遇陣風，車體受隨機力向轉向架、輪對傳遞力及力矩，使輪對搖頭運動、列車蛇行運動加劇，嚴重時使輪軌間輪緣接觸擠壓、輪軌橫向作用力加劇磨損，甚至輪軌瞬時分離發生傾覆。選定平均風速12 m/s和風向角α=90°、γ=0°，列車勻速Uv=200 km/h（55.56 m/s），直線行駛。

對比計算列車行車有無陣風激擾，時頻響應分析取頭車T1作為代表，結果如圖5所示。時域上看，無風時列車經過該路段只受軌道不平順激擾，而有風工況時域曲線變為脈動橫風激擾主導成明顯的加載、穩定、卸荷過程，車體動力學響應明顯增大，脫軌系數由0.055增至0.082，車體橫向加速度值由0.032 g增至0.039 g。

圖5 脈動橫風對車輛受迫振動影響

頻域上看，陣風主要激起了車體結構低頻振動，尤其是3 Hz以下模態激發最為顯著，1 Hz前后出現明顯峰值，分析可知陣風作為橫向外力最終作用于剛性輪對，導致左右輪產生輪徑差［15］，輪對未處于徑向位置，因縱向蠕滑的存在，導致輪對產生較大的搖頭運動以抵消橫向外力，此時激勵頻率與二階搖頭模態構成共振，導致在1 Hz左右的頻率幅值猛增。

3.2 脈動橫風對編組內車輛的影響

該列車采用四動四拖八輛編組形式，各車車體參數、轉向架參數、迎風面積，尤其是遭遇橫風時的氣動系數等均有所不同，此時各車輛響應也不盡相同。本節計算中平均風速12 m/s和風向角α=90°和γ=0°，列車勻速Uv=200 km/h（55.56 m/s），直線行駛，計算結果如表5所示。

表5 陣風激擾下車輛動力學響應計算結果

由表5所示結果可以看出，加載脈動橫風后各車響應均大幅增加，車體響應中，車輛橫向加速度、車體垂向平穩性指標等都是頭車T1最為明顯，而車體垂向加速度則是T4最為敏感。輪軌響應中，輪軌橫向力T4受脈動橫風影響最大，垂向力為M6最敏感，輪重減載率為T1最敏感，脫軌系數為M7最大。可以看出，這是由于陣風在空間分布的相關性、車輛參數不同、氣動系數差異等綜合作用結果，多數情況下頭車T1受橫風影響最為顯著。

4 脈動橫風下列車運行限值管理

4.1 脈動橫風下的車速限值

基于上述模型及橫風激擾基本特性，研究脈動橫風下不同車速的影響及其閾值，本節平均風速12 m/s，列車車速Uv從150 km/h（41.67 m/s）到400 km/h（111.11 m/s），其余參數與此前相同，計算后提取頭車計算結果，如圖6所示。

從圖6可以看出，脈動橫風激擾下的頭車T1的動力學響應峰值隨著車速的增大而不同程度地增加，平穩性與車速強負相關。車體橫向平穩性指標（閾值2.75）及輪重減載率ΔP/ˉP（閾值0.8）對脈動橫風激擾下的車速變化最為敏感，臨界車速分別為395和355 km/h，即當預設下（最大風速12 m/s時），最大車速達到355 km/h時輪重減載率已超標［16］。

4.2 脈動橫風下的風速限值

繼續分析脈動橫風不同平均風速的影響及其閾值，本節平均風速為0.1～35 m/s，列車車速Uv=200 km/h（55.56 m/s），其余參數與此前相同，提取頭車計算結果如圖7所示。

由圖7可知，風速規律與車速一致，脈動橫風激擾下的頭車T1的動力學響應峰值隨著風速的增大而不同程度地增加，平穩性與風速負相關。其中輪軌響應中的輪重減載率ΔP/ˉP（閾值0.8）對脈動橫風風速變化最為敏感，臨界平均風速為33.5 m/s，即當預設下（車速200 km/h時），最大平均風速達到33.5 m/s時輪重減載率已超標［16］。

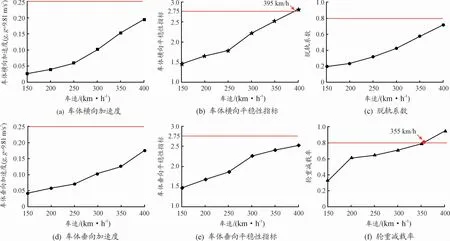
圖6 脈動橫風下的車速影響規律及其限值

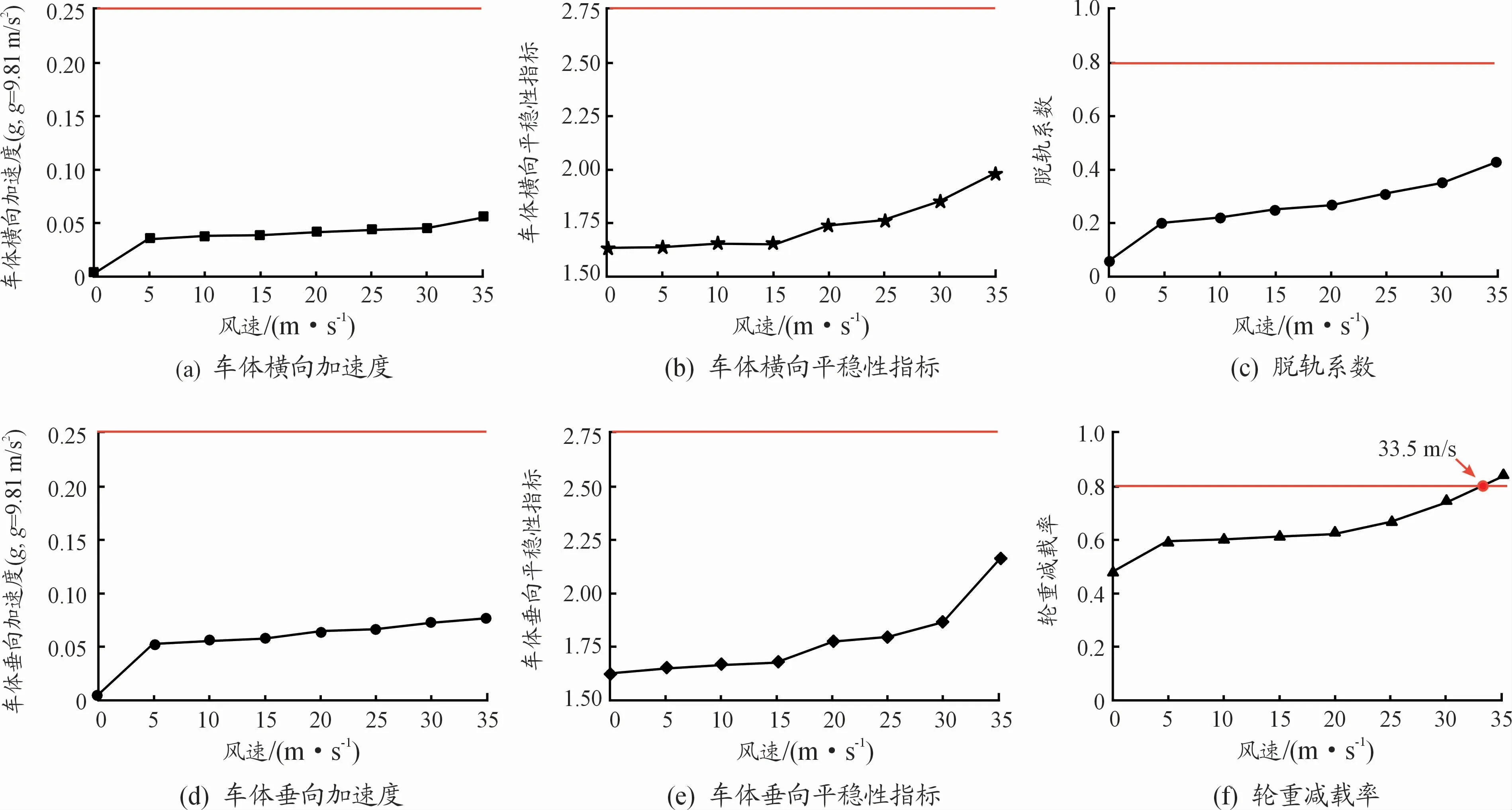
圖7 脈動橫風風速影響規律及其限值

5 結論

1）基于多體動力學方法與隨機風速模擬方法，可以有效脈動橫風下的列車運行特性，并在此基礎上快速獲得列車動力學響應以進行科研分析。

2）空間脈動橫風載荷加劇了車輛3 Hz內低頻振動并激起了1 Hz附近的峰值區，風-車參數差異導致列車編組內響應呈現差異，多數情況下頭車T1對橫風最敏感。

3）車輛運行速度和橫風平均風速的增長都會使車輛平穩性迅速變差，各自計算條件下，最大車速限值為355 km/h，最大風速限值為33.5 m/s。