基于模型預(yù)測控制的電動汽車起步工況仿真與性能評價

李文禮，陸 宇，汪楊凡，鄭維東，嚴海燕，徐 瑞

（1.重慶理工大學(xué) 汽車零部件先進制造技術(shù)教育部重點實驗室，重慶 400054；2.大陸汽車研發(fā)（重慶）有限公司，重慶 404100；3.東風(fēng)汽車股份有限公司 東風(fēng)商品研發(fā)院，武漢 430056）

近年來，電動汽車由于具有節(jié)能、環(huán)保、能量效率高等優(yōu)點，在國內(nèi)發(fā)展迅速。相對于傳統(tǒng)燃油汽車，電動汽車的電驅(qū)動系統(tǒng)沒有離合器的輔助，如果缺乏合理的控制策略，會在啟動過程中出現(xiàn)抖動現(xiàn)象，因此汽車起步工況是電動汽車電驅(qū)動系統(tǒng)的重要工況，其性能反映了電驅(qū)動系統(tǒng)及整車的控制策略優(yōu)劣，對電動汽車起步過程的研究具有重要意義［1-6］。

國內(nèi)外學(xué)者對汽車起步控制進行了較為深入的研究。胡建軍等［4］在考慮駕駛員意圖的基礎(chǔ)上，提出純電動汽車無油門起步和有油門起步兩種模式下的起步控制策略，仿真結(jié)果表明所提出的控制策略充分反映了駕駛員意圖，控制效果理想。吳兵顯等［5］提出一種驅(qū)動電機和制動器相配合的自適應(yīng)起步控制方法，從起步?jīng)_擊度和溜坡距離兩個坡道起步評價指標(biāo)驗證了所提出控制方法的有效性。羅石等［6］根據(jù)加速踏板開度與加速踏板開度變化率制定基于模糊推理的駕駛員意圖解析策略，并基于該策略和車輛實際運行情況制定電機轉(zhuǎn)矩的控制策略，從速度、電機輸出轉(zhuǎn)矩和沖擊度3個方面驗證控制策略的可行性。秦大同等［7］針對不同的駕駛員意圖起步操作模式，分別制定相應(yīng)的控制策略，提高了純電動汽車起步時的動力性和操控性。近年來，很多學(xué)者把模型預(yù)測控制（model predictive control，MPC）策略應(yīng)用在汽車控制領(lǐng)域，獲得了較好的效果。辛喆等［8］利用MPC方法實現(xiàn)了智能汽車的軌跡跟蹤，同時保證了智能汽車行駛穩(wěn)定性和安全性。謝輝等［9］針對具有高度非線性、強耦合的無人駕駛汽車運動控制問題，提出一種基于MPC的橫縱向綜合控制方法，實現(xiàn)了車輛的速度跟蹤。李紹松等［10］提出一種改進型線性時變MPC方法，提高了極限工況下主動前輪轉(zhuǎn)向汽車的穩(wěn)定性。唐小林等［11］在多車速度規(guī)劃與跟馳模型基礎(chǔ)上設(shè)計了MPC算法來規(guī)劃汽車隊列的未來車速，以達到提高混合動力汽車車隊的跟車穩(wěn)定性的目的。

MPC方法可以很好地處理各種帶約束的線性、非線性問題。為提高電動汽車起步工況下的性能，采用MPC方法對電動汽車起步過程進行控制。首先建立純電動汽車整車模型和駕駛員模型，基于MPC方法建立的駕駛員模型利用上層控制器得到期望加速度，下層控制器根據(jù)期望加速度得到加速指令和減速指令，從而對車輛進行起步工況的加、減速控制。給出起步時間、驅(qū)動電機電壓電流和沖擊度3個評價指標(biāo)，分別進行不同坡度（0%，10%和20%）下電動汽車起步工況的仿真試驗，并根據(jù)評價指標(biāo)對試驗結(jié)果進行分析。

1 純電動汽車整車模型

為了進行電動汽車起步工況的仿真試驗，需要建立純電動汽車整車模型，主要包括整車控制器模型、驅(qū)動電機模型、傳動系和輪胎模型［12］。

1.1 整車控制器模型

整車控制器是純電動汽車的核心控制部件，本文中根據(jù)仿真需求對整車控制器模型進行簡化，主要結(jié)構(gòu)包括如圖1所示的根據(jù)踏板開度計算電機轉(zhuǎn)矩需求模塊。

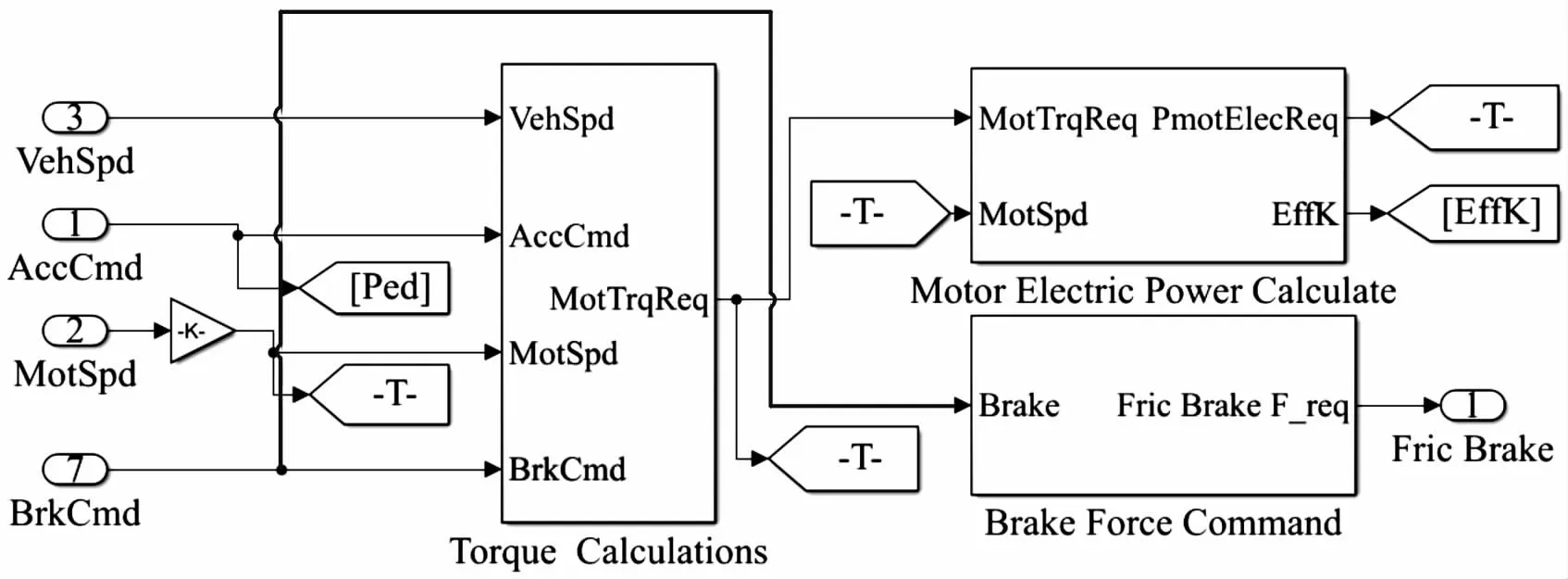
圖1 電機轉(zhuǎn)矩需求計算模塊示意圖

1.2 驅(qū)動電機模型

選取永磁同步電機作為電動汽車驅(qū)動單元進行建模，其數(shù)學(xué)模型主要包括電壓平衡方程、磁鏈方程和轉(zhuǎn)矩方程。一般對驅(qū)動電機數(shù)學(xué)模型進行簡化分析，做以下假設(shè)［13］：

1）定子繞組為Y型連接，三相繞組對稱分布，各個繞組的軸線在空間互差120°；

2）不計轉(zhuǎn)子阻尼；

3）忽略電機中的渦流和磁滯損耗。

4）忽略繞組電阻與電感的變化；

1.2.1 電壓平衡方程

根據(jù)永磁同步電機原理，定子電壓平衡方程表示為：

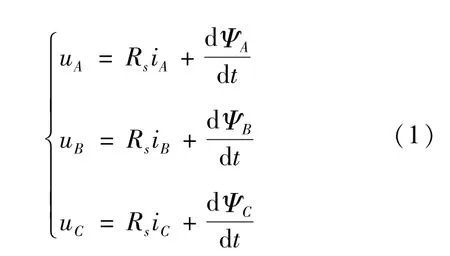
式中：uA、uB、uC為三項繞組各相的電壓；Rs為三相繞組電阻；iA、iB、iC為三項繞組各相的電流；ΨA、ΨB、ΨC為三項繞組各匝鏈磁鏈。

1.2.2 磁鏈方程

磁鏈又稱為磁通匝，其方程表達式為：

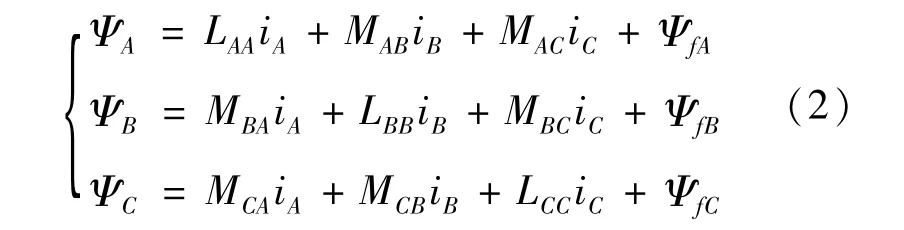
式中：LAA、LBB、LCC為三相定子繞組自感；MAB=MBA、MBC=MCB、MCA=MAC為每項繞組互感；ΨfA、ΨfB、ΨfC為轉(zhuǎn)子勵磁磁場匝鏈至定子繞組的磁鏈。

1.2.3 轉(zhuǎn)矩方程

假設(shè)電機運行時電流一定，電磁轉(zhuǎn)矩可以表示為磁場儲能對機械角度θm的偏導(dǎo)，則電磁轉(zhuǎn)矩Te表示為：

式中：np為極對數(shù)；［L］為電機自感和互感矩陣；［Ψ（θe）］為電機永磁轉(zhuǎn)子磁鏈矩陣；θe為電氣角度。

1.3 傳動系統(tǒng)和輪胎模型

傳動系采用前驅(qū)單速比機械式變速器，驅(qū)動電機輸出動力給變速器，經(jīng)差速器后傳遞給車輪，因此，建立的純電動汽車傳動系統(tǒng)模型如圖2所示。

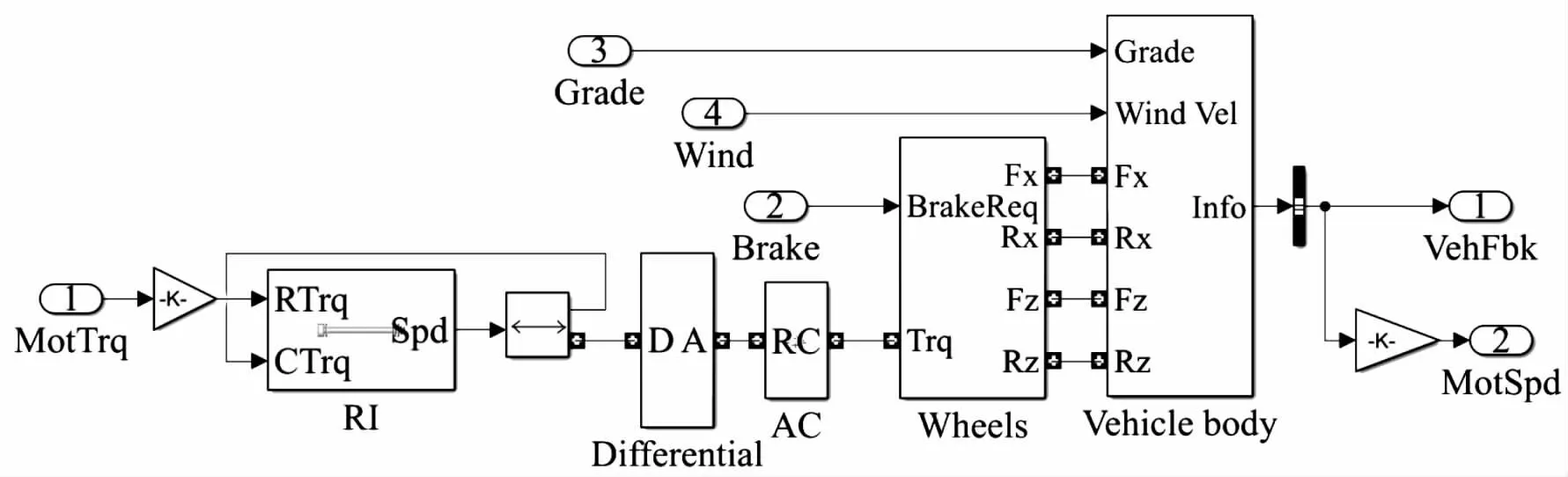
圖2 純電動汽車動力傳動系統(tǒng)模型示意圖

純電動汽車起步過程仿真中，為了更加準(zhǔn)確地反映實際道路情況，對輪胎模型精度有較高要求，這里選取魔術(shù)公式的輪胎模型進行建模。魔術(shù)公式的原理［14］是利用三角函數(shù)組合的形式來擬合輪胎的試驗數(shù)據(jù)，進而得到一套形式相同的公式來表達輪胎的側(cè)向力、縱向力、回正力矩、翻轉(zhuǎn)力矩、阻力矩以及側(cè)向力、縱向力聯(lián)合作用等工況。魔術(shù)公式的一般表達形式為［15］：

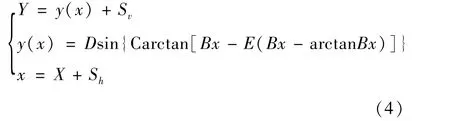
式中：Y為側(cè)向力、縱向力或回正力矩；X為側(cè)偏角或縱向滑移率；D為峰值因子；B為剛度因子；C為曲線形狀因子；E為曲線曲率因子；Sh、Sv分別為曲線水平方向及垂直方向的漂移。

圖3為建立的輪胎動力學(xué)模型示意圖。

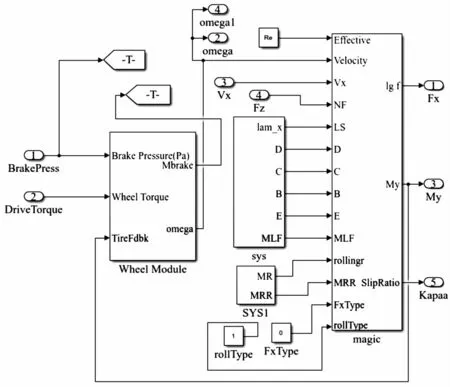
圖3 輪胎動力學(xué)模型示意圖

2 駕駛員模型

2.1 駕駛員意圖解析

車輛在行駛過程中，駕駛員通過將其主觀意愿和周圍實時道路情況相結(jié)合對車輛進行加速、減速和轉(zhuǎn)彎等操作。為了簡化駕駛員意圖，可將其轉(zhuǎn)化為加速踏板開度變化和制動踏板開度變化，即當(dāng)駕駛員期望加速時加大加速踏板、松開制動踏板，當(dāng)駕駛員期望減速時松開加速踏板、加大制動踏板。

2.2 基于MPC的駕駛員模型設(shè)計

圖4為基于MPC的駕駛員模型結(jié)構(gòu)。其中上層控制器基于MPC方法得到期望加速度，下層控制器根據(jù)期望加速度得到加速指令和減速指令，從而對車輛進行自動加、減速控制［9，16-18］。

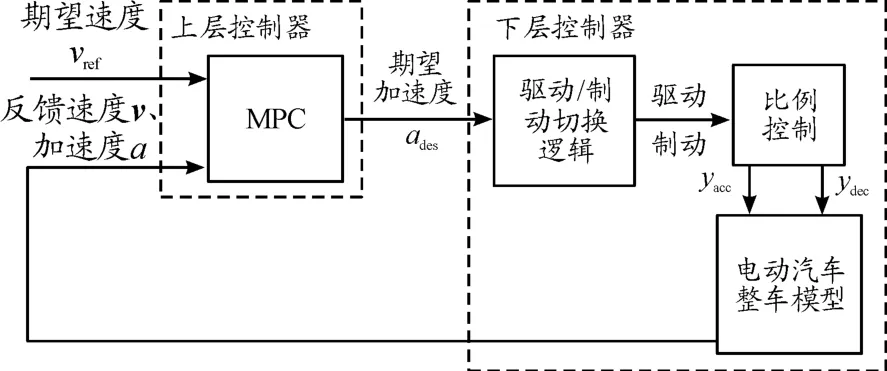
圖4 基于MPC的駕駛員模型結(jié)構(gòu)框圖

2.2.1 層控制器設(shè)計

車輛的期望加速度ades與實際加速度a之間的關(guān)系可由1階慣性環(huán)節(jié)來近似表示［17］：

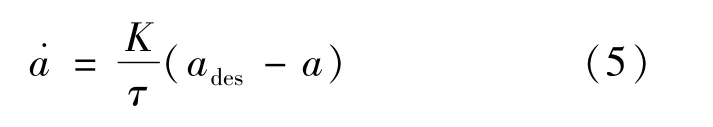
式中：K為系統(tǒng)增益；τ為時間常數(shù)。其連續(xù)系統(tǒng)的狀態(tài)空間方程可表示為：

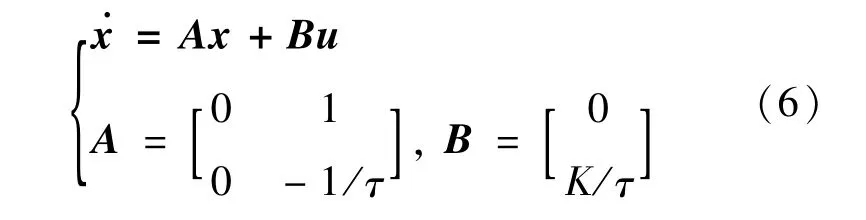
式中：x=［v a］T為系統(tǒng)狀態(tài)變量；u=ades為系統(tǒng)控制輸入。

對式（6）進行離散化處理，得到離散系統(tǒng)的狀態(tài)空間方程為：

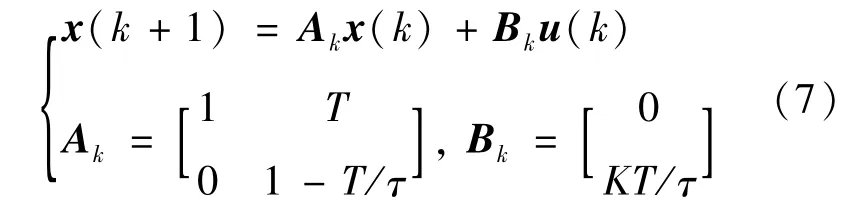
式中：k為當(dāng)前采樣時刻，k+1為下一個采樣時刻；T為采樣周期。

控制系統(tǒng)的輸出變量為速度，則輸出方程可以表示為：

式中，Ck=［1 0］。

考慮到系統(tǒng)控制目標(biāo)為在不產(chǎn)生較大加速度及加速度變化率的前提下實現(xiàn)縱向速度的精確跟蹤，設(shè)計優(yōu)化目標(biāo)函數(shù)為：

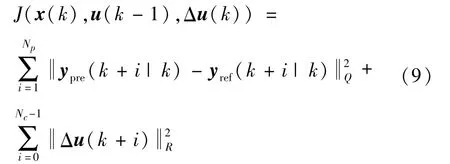
式中：k-1為上一個采樣時刻；Np為預(yù)測時域，Nc為控制時域；ypre（k+i|k）為系統(tǒng)輸出變量的預(yù)測值，yref（k+i|k）為系統(tǒng)輸出變量的參考值，（k+i|k）表示以k時刻的系統(tǒng)輸出量來預(yù)測k+i時刻的值，其中i=1，2，…，Np；Δu（k）和Δu（k+i）分別為k時刻和k+i時刻系統(tǒng)控制輸入增量，即加速度增量，其中i=0，1，…，Nc-1；Q和R為權(quán)重矩陣。

系統(tǒng)需要對控制輸入的加速度及其增量施加約束條件，即：

式中：umin和umax分別為加速度的閾值；Δumin和Δumax分別為加速度增量的閾值。

系統(tǒng)優(yōu)化求解問題即在預(yù)測時域里，式（9）在滿足式（10）的約束條件下達到最小。通過將上述問題轉(zhuǎn)化為Matlab易于求解的二次規(guī)劃問題，得到控制時域內(nèi)的系統(tǒng)控制輸入增量為：

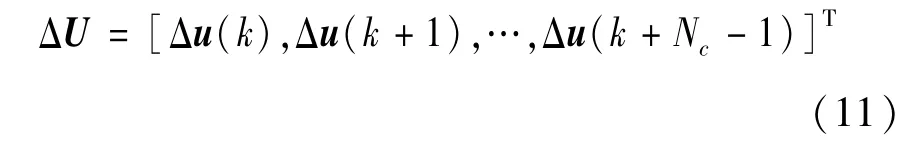
將控制輸入增量的第1項Δu（k）取出，即可得到當(dāng)前時刻系統(tǒng)控制輸入為：

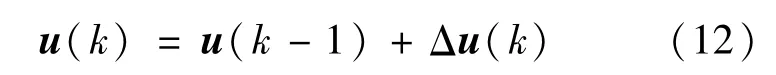
2.2.2 下層控制器設(shè)計

下層控制器由驅(qū)動、制動切換邏輯和比例控制模塊組成［17］。切換邏輯為將從上層控制器獲得的期望加速度ades與0相比較。當(dāng)ades≥0時施加驅(qū)動控制（驅(qū)動模式），當(dāng)ades＜0時施加制動控制（制動模式）。由于用于仿真研究的電動汽車整車模型的輸入量為yacc（即加速踏板開度）和ydec（即制動踏板開度），所以可通過簡單的比例控制計算驅(qū)動、制動控制輸入量。

驅(qū)動模式時，由上層控制器得到ades，則制動控制輸入為ydec=0，加速踏板開度αdes=Kt×ades，Kt為加速踏板開度轉(zhuǎn)換比例，則驅(qū)動控制輸入為：

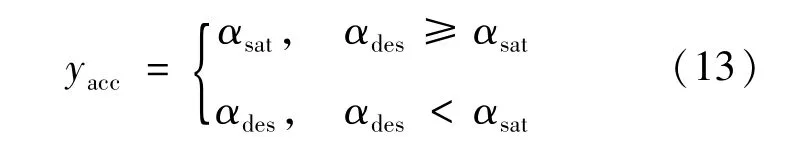
式中，αsat為加速踏板開度閾值。

制動模式時由上層控制器得到ades，則驅(qū)動控制輸入為yacc=0，制動踏板開度βdes=Kb×ades，Kb為制動踏板開度轉(zhuǎn)換比例，則制動控制輸入為：

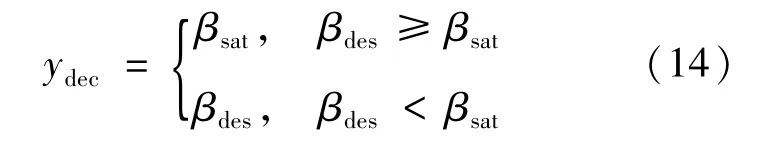
式中，βsat為制動踏板開度閾值。

如圖5所示，上層控制器基于S函數(shù)建立了基于MPC的駕駛員模型。

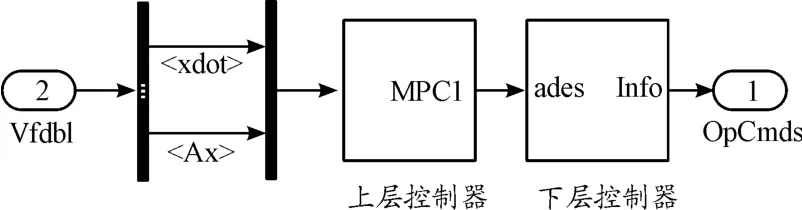
圖5 基于模型預(yù)測控制的駕駛員模型框圖

3 純電動汽車起步性能評價指標(biāo)

為了驗證提出的基于MPC方法的駕駛員模型在純電動汽車起步工況仿真中控制性能的有效性，從起步時間（動力性）、驅(qū)動電機電壓和電流（經(jīng)濟性）、沖擊度（舒適性）3個方面對純電動汽車起步性能進行評價。

3.1 起步時間

由GB/T 28382—2012所要求的動力性能可知，車輛最大爬坡度不低于20%。按規(guī)定的試驗方法對純電動汽車0～80 km/h的起步加速性能進行測試時，起步加速時間不超過25 s。

3.2 驅(qū)動電機電壓和電流

純電動汽車起步過程中，驅(qū)動電機電壓和電流會出現(xiàn)較大波動。當(dāng)驅(qū)動電機電壓過低時，起動轉(zhuǎn)矩不足會導(dǎo)致電機啟動困難；當(dāng)驅(qū)動電機電流過高時，定子線圈會因過流而發(fā)生斷路等故障。因此，車輛起步過程中，驅(qū)動電機電壓和電流不易過高，以免影響其壽命。

3.3 沖擊度

沖擊度是評價純電動汽車起步品質(zhì)的一項重要指標(biāo)，根據(jù)國家對車輛起步時沖擊度的要求，設(shè)定推薦值在10 m·s-3以內(nèi)。根據(jù)汽車行駛方程：

式中：ig為變速器傳動比；i0為主減速器傳動比；η為傳動效率；r為車輪半徑；G為整車重力；f為滾動阻力系數(shù)；θ為道路坡度角；CD為空氣阻力系數(shù)；A為迎風(fēng)面積；v為當(dāng)前車速；δ為車輛旋轉(zhuǎn)質(zhì)量換算系數(shù)；m為車輛質(zhì)量；d v/d t為車輛當(dāng)前加速度。

由式（15）可得：

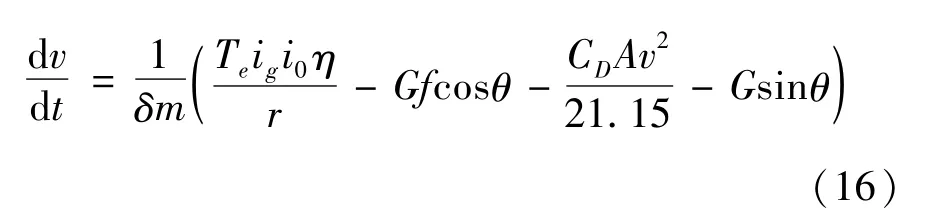
假設(shè)坡度阻力和滾動阻力的數(shù)值保持不變，忽略風(fēng)阻，對式（16）求導(dǎo)可得沖擊度j為：

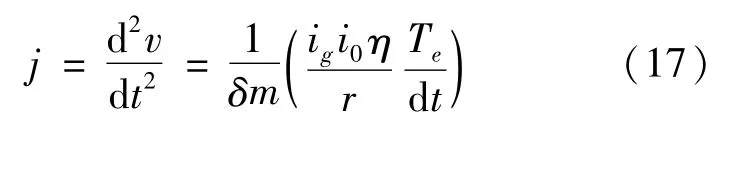
4 仿真及結(jié)果分析

在Matlab/Simulink中建立如圖6所示的純電動汽車整車模型用于仿真研究，部分仿真整車參數(shù)如表1所示。

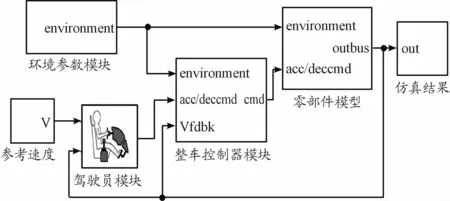
圖6 純電動汽車整車模型框圖

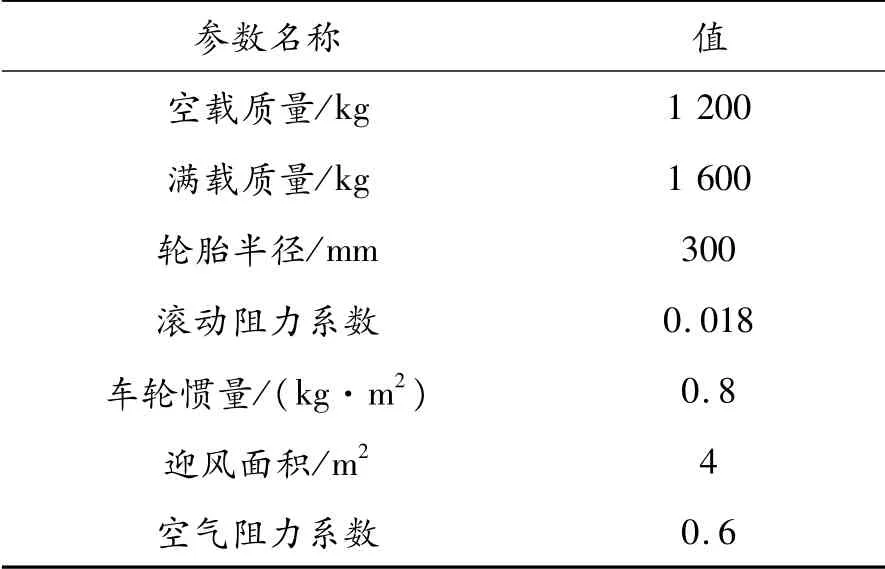
表1 整車參數(shù)

為了較好地研究純電動汽車起步過程的各項性能指標(biāo)，對提出的基于MPC方法的駕駛員模型進行不同坡度下起步過程的仿真，并與常規(guī)PID控制的駕駛員模型的控制性能進行比較。仿真參數(shù)及試驗工況設(shè)置為：

1）Simulink仿真環(huán)境：參考GB/T 28382—2012的動力性能要求以及乘車舒適度，為較好反映純電動汽車起步工況，仿真時長設(shè)為20 s，第10 s的期望車速設(shè)為15 km/h，設(shè)定采樣時間為0.001 s；

2）PID控制器參數(shù)：比例系數(shù)設(shè)為1.5，積分系數(shù)設(shè)為1.5，微分系數(shù)設(shè)為0；MPC控制器參數(shù)：預(yù)測時域設(shè)為30，控制時域設(shè)為15，權(quán)重取值Q=100，R=1；

3）試驗工況：設(shè)置在3種路面上進行起步工況仿真試驗，即路面的坡度分別設(shè)為0%、10%及20%。

根據(jù)設(shè)置的仿真參數(shù)及試驗工況進行仿真試驗，得到的仿真結(jié)果如圖7～12所示，其中圖7～10均為車輛空載時在不同坡度下起步的仿真結(jié)果。由圖7、8可知，分別使用MPC和PID控制方法的駕駛員模型進行仿真時，在起步初期，坡度越大，電壓電流變化越大，但電機電壓、電流均在正常變化范圍內(nèi)。在達到目標(biāo)車速后，電機電壓、電流有所波動，PID控制方法下的曲線的超調(diào)量大于MPC方法。由圖9、10可知，2種控制方法起步響應(yīng)時間均為11 s左右，起步響應(yīng)達到預(yù)期控制效果，使用MPC方法的駕駛員模型時起步響應(yīng)更快，其超調(diào)量也小于PID控制方法。

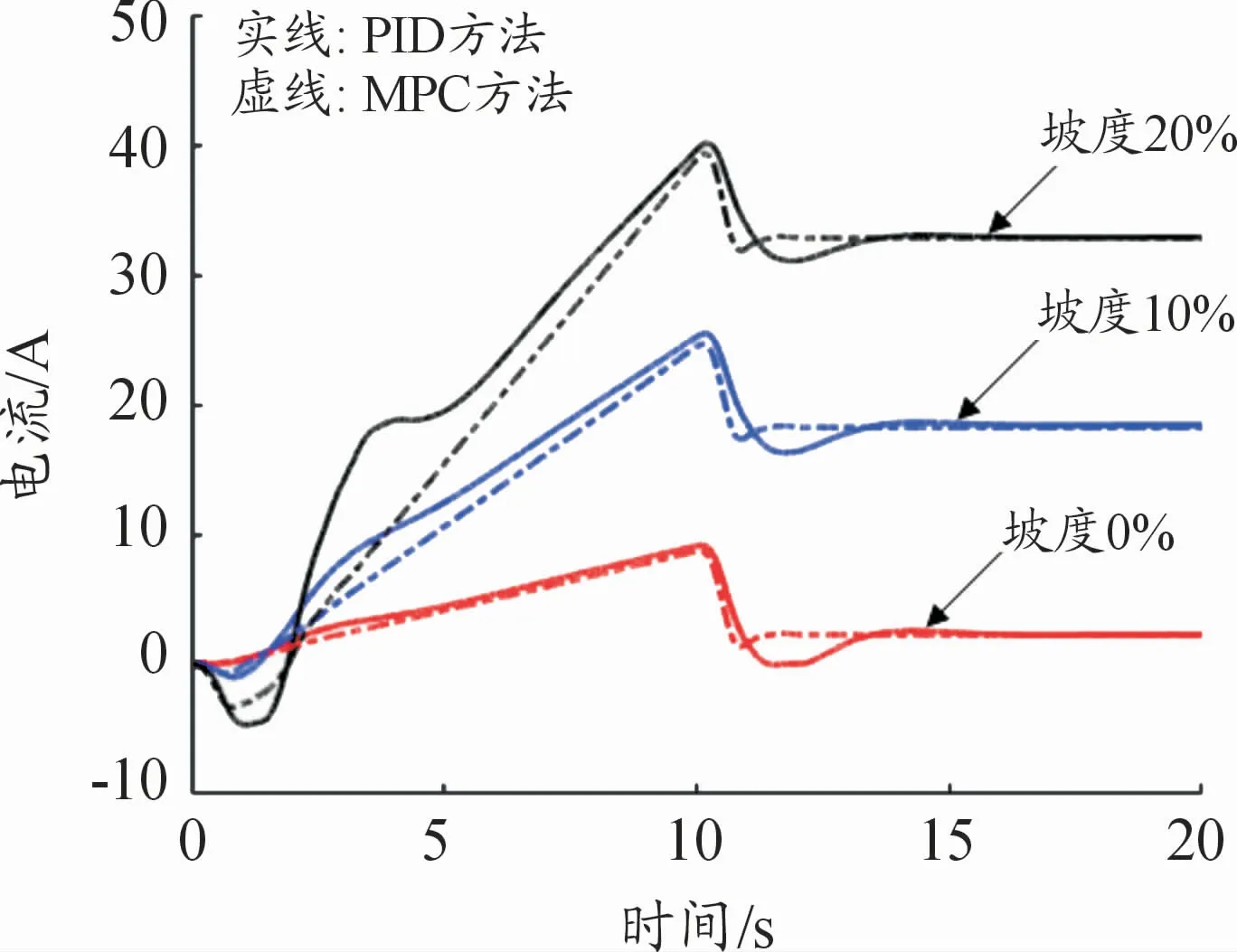
圖7 不同坡度下起步驅(qū)動電機電流仿真結(jié)果

圖8 不同坡度下起步驅(qū)動電機電壓仿真結(jié)果

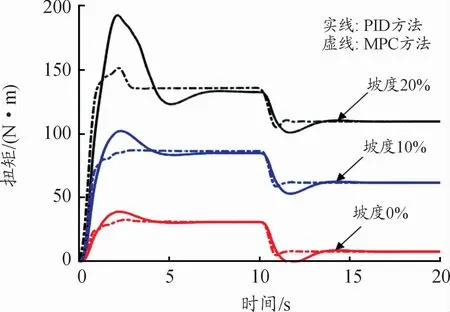
圖9 不同坡度下起步驅(qū)動電機扭矩仿真結(jié)果

圖10 不同坡度下起步驅(qū)動電機轉(zhuǎn)速仿真結(jié)果

考慮車輛負載對起步性能的影響，圖11～12為加入不同負載（空載、半載和滿載）的車輛在10%坡度下起步時的仿真結(jié)果。由圖11、12可知：在設(shè)定的駕駛員期望車速及起步時間一致的情況下，加速踏板開度仿真結(jié)果可以較真實地反映駕駛員在不同坡度下起步時的操控過程，加速踏板開度隨著車輛負載增加而增大。起步初期0～6 s內(nèi)，沖擊度較大，且最大值出現(xiàn)在20%的坡度下起步時，MPC方法下的駕駛員模型的瞬時最大值約為3.9 m·s-3，PID控制方法下的駕駛員模型的瞬時最大值約為4.1 m·s-3，均低于國家對車輛起步時沖擊度設(shè)定的推薦值10 m·s-3；隨著車輛負載的增加，2種控制方法下的最大沖擊度都會相應(yīng)增加，在10%坡度下起步時均低于3 m·s-3；在6～9 s內(nèi)，車輛處于短暫的勻加速行駛階段，沖擊度變化較小；在9～13 s內(nèi)，車輛達到設(shè)定的駕駛員期望車速15 km/h，為了保持該車速，驅(qū)動電機的扭矩需求變小，從而使得沖擊度較大；在13 s后車輛勻速行駛，沖擊度較小。

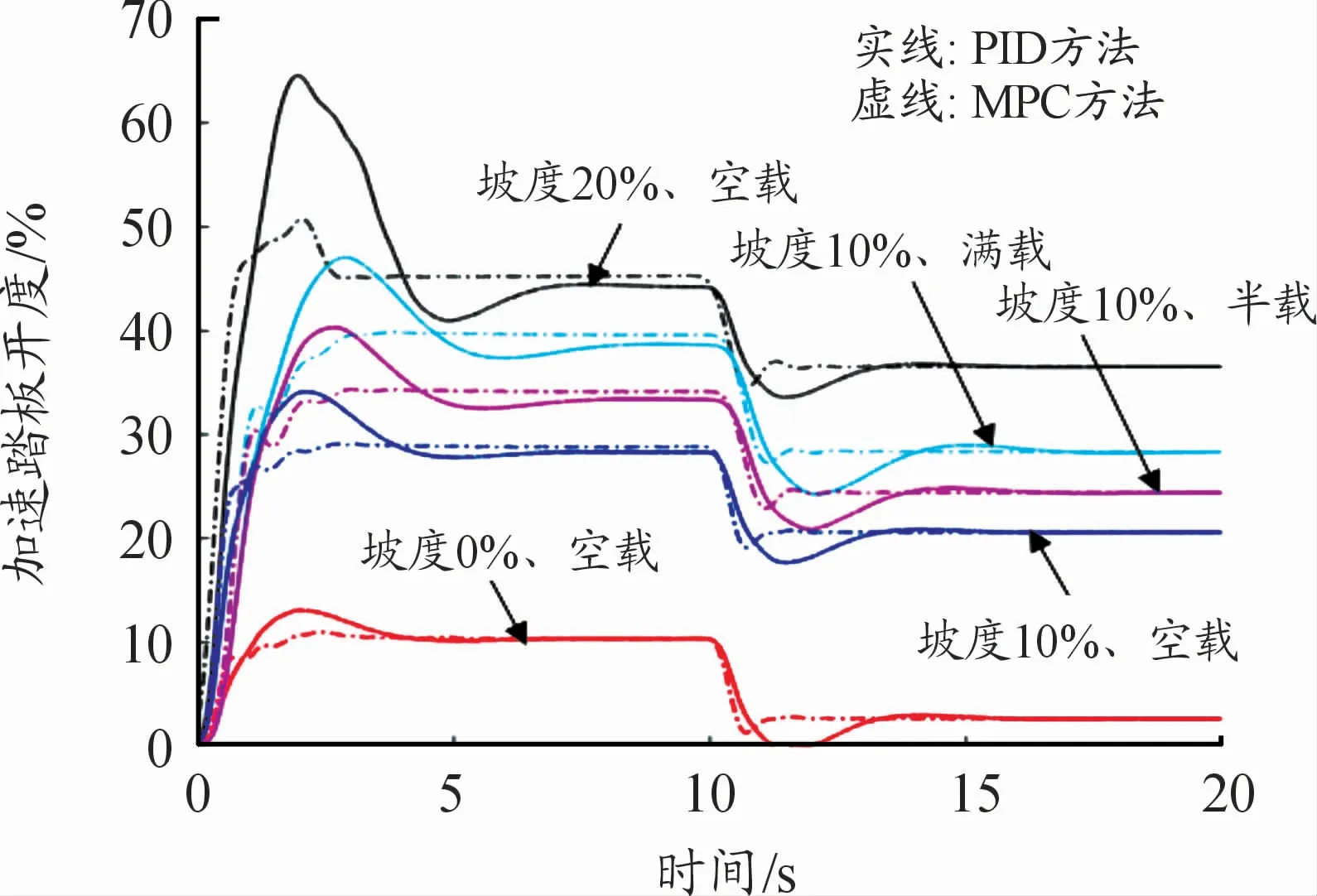
圖11 不同坡度下起步加速踏板開度仿真結(jié)果

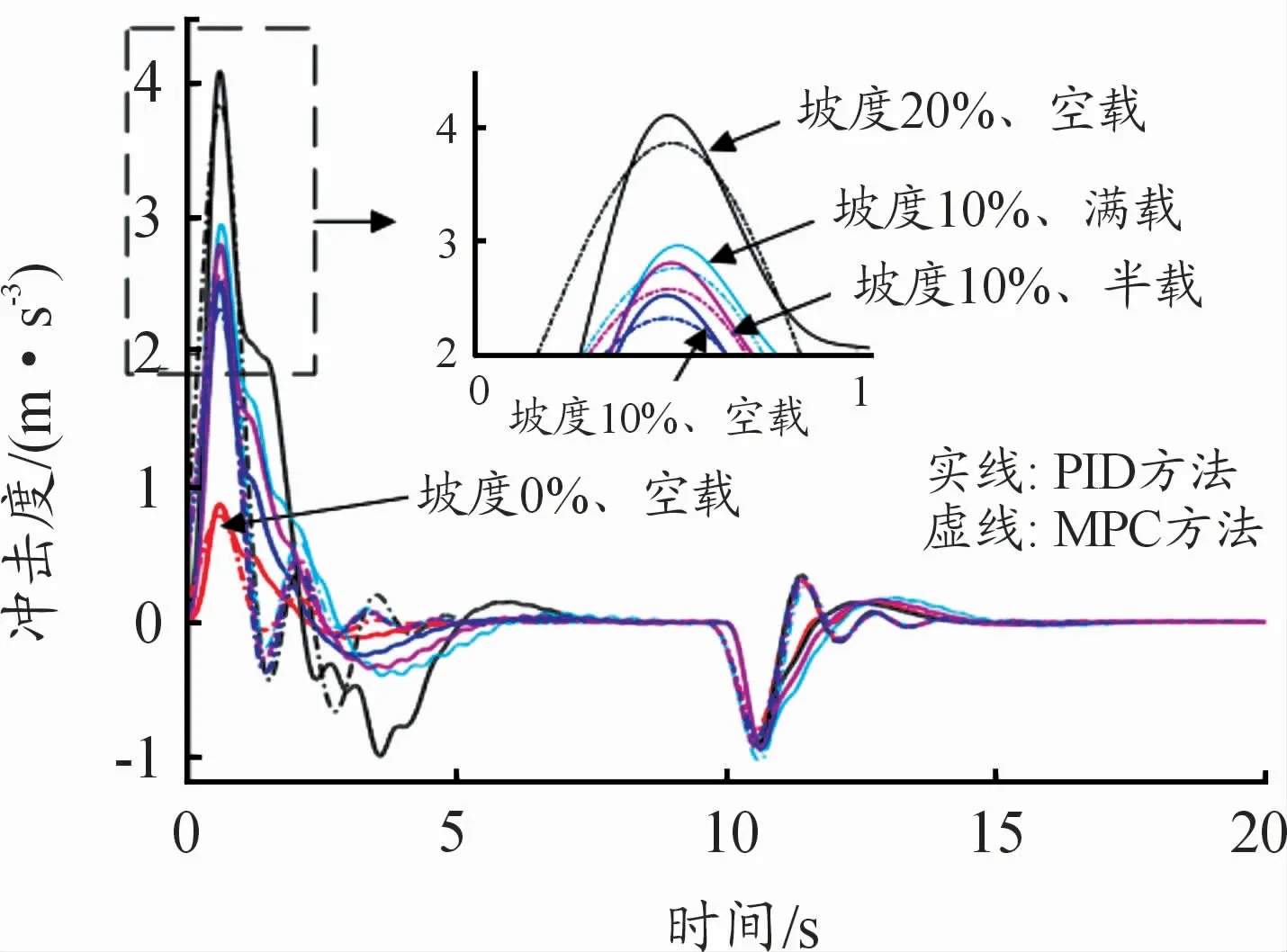
圖12 不同坡度下起步?jīng)_擊度仿真結(jié)果

5 結(jié)論

提出一種基于MPC的駕駛員模型，用于電動汽車起步工況仿真的控制性能研究。建立了較為完整的純電動汽車整車模型和駕駛員模型，其中駕駛員模型包括上層控制器和下層控制器。上層控制器基于MPC方法求出期望加速度，下層控制器則由期望加速度來判斷驅(qū)動、制動切換邏輯，求出純電動汽車整車模型在進行起步工況仿真時需要的加、減速指令，進而得到電機需求轉(zhuǎn)矩。

給出了起步時間、驅(qū)動電機電壓電流和沖擊度3個純電動汽車起步性能評價指標(biāo)，分別在不同坡度（0%，10%和20%）下進行起步工況的仿真試驗。利用試驗結(jié)果在給出的起步性能評價指標(biāo)下分析了基于MPC的駕駛員模型的控制性能，并與常規(guī)基于PID控制的駕駛員模型的控制性能進行了比較。仿真結(jié)果驗證了基于MPC的駕駛員模型在起步工況仿真中控制性能的有效性，所提出的仿真方法可為電動汽車電驅(qū)動系統(tǒng)性能研究提供參考。