基于高增益觀測器的挖掘機工作裝置滑模控制
徐國勝, 於祖慶, 陸念力, 呂廣明
(哈爾濱工業大學 機電工程學院,黑龍江 哈爾濱 150001)
挖掘機自動控制一直是工程領域研究的熱點。文獻[1-4]采用滑模變結構或其與模糊邏輯、自適應理論的結合,調節挖掘機輸入轉矩,使關節轉角跟蹤規劃值,仿真結果證明了算法有效性。挖掘機工作裝置由單活塞桿液壓缸驅動,相較于電機驅動的機械臂,由于液壓缸系統的非線性,采用關節轉矩作為輸入,控制不直接且控制精度低,使關節轉角實際軌跡與規劃軌跡存在很大誤差,進而使鏟斗斗尖在工作空間不能有效跟蹤規劃路徑。為此,文獻[5]分析了某機械臂系統液壓伺服驅動空間與關節空間關系,以關節轉矩為紐帶,建立輸入伺服電流與輸出關節轉角間的數學模型,從而將控制器設計轉移到伺服驅動空間。
針對液壓伺服系統的控制,阻抗滑模控制[6]、高階滑模控制[7]、非連續投射[8-9]、及其與滑模控制的結合[10]、反饋線性化滑模控制[11-13],被廣泛應用并取得較好的仿真試驗效果。然而上述控制方式需要采集活塞桿位移、速度或加速度,以及液壓缸兩腔壓力信號,增加了控制成本。為降低傳感器使用數量,觀測器被引入至控制器的設計,用來對狀態變量或干擾進行觀測[14-19]。文獻[14]基于投射法對干擾進行觀測,文獻[15]基于低通濾波對速度觀測,文獻[16]基于擴張觀測器對狀態變量及干擾觀測,并采用反演法設計液壓系統控制器。相較于上述觀測器,高增益觀測器能夠對控制所需的所有狀態信息進行有效估計,且設計更為簡單,容易實現。文獻[17]構造了基于高增益狀態觀測器的電液系統無源控制器,仿真與試驗驗證了控制輸出活塞桿位移對目標位移信號優良的跟隨性能。文獻[18]設計了基于高增益觀測器的積分滑模控制器,并采用奇異攝動理論證明了閉環系統的穩定性。文獻[19]針對電液系統構造了基于高增益觀測器的反演控制器,仿真與試驗效果較好。
本文通過計算挖掘機關節空間與驅動空間的位移、速度與力之間的關系,得到控制輸入伺服閥電壓與關節轉角之間的關系。采用基于高增益觀測器的滑模控制理論,對驅動空間電液系統進行軌跡控制。并采用奇異攝動方法,將觀測器狀態觀測誤差與系統控制誤差分別作為快變子系統變量與慢變子系統變量,基于李雅普諾夫函數,證明閉環系統穩定。相較于文獻[18],本文采用文獻[20]中高增益觀測器的設計方法,只需調節觀測器帶寬參數,不需整定其他增益參數,因而觀測器設計更加簡便;在滑模控制中,采用滑模面函數代替符號函數,消除了抖振且對閉環系統穩定性有重要作用;在液壓系統中引入匹配不確定項與非匹配不確定項,通過定義新的狀態變量,對非匹配不確定項補償。仿真結果表明本文設計的基于高增益觀測器的滑模控制器效果較好,且對匹配與非匹配不確定項有良好的魯棒性。
1 挖掘機規劃軌跡生成
1.1 挖掘機驅動空間與關節空間關系
圖1為挖掘機工作裝置模型,采用D-H方法建立了系統坐標。
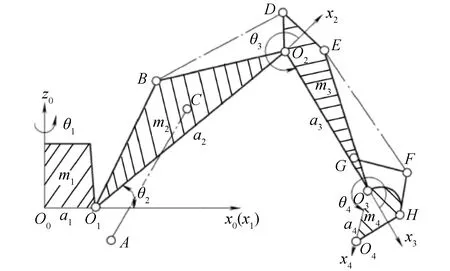
圖1 挖掘機工作裝置模型Fig.1 Coordinate frames of the excavator
則挖掘機關節空間關節轉角與驅動空間液壓缸活塞桿長度之間的關系:
(1)
式中:∠CO1O2、∠AO1x1、∠O1O2B、∠DO2O3、∠GO3O2、 ∠HO3O4、∠EGO2、∠O2GO3與桿長lO1C、lO1A、lO2D、lO2B、lGE、lGF、lO3G、lO3H、lFG、lFH為常量,代入本文研究對象柳工某型液壓挖掘樣機參數,得到關節轉角與對應液壓缸活塞桿長度曲線如圖2所示。
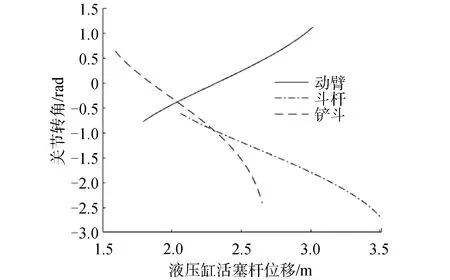
圖2 液壓挖掘機活塞桿位移與對應轉角關系Fig.2 The relationship between piston rod displacement and corresponding rotation angle
由虛功原理,關節轉矩與驅動力關系表示為:
(2)

(3)
式中:φ2=θ2+∠CO1O2+∠AO1x1,φ3=θ3+∠O1O2B+∠DO2O3,φ2=θ4+∠EO3O2+∠HO3O4。由式(1),θ4與lEF之間機構連接關系導致雅克比矩陣J中J3項表達復雜,在誤差可控條件下,采用θ4與lEH的雅克比關系代替(或直接由圖2曲線函數擬合后求導得到對應各關節轉角的雅克比項)。
1.2 挖掘機驅動空間軌跡規劃
挖掘機不考慮回轉時,其鏟斗末端軌跡在基坐標系O0x0y0z0(圖1)中表示為:
(4)
式中:a1為動臂鉸接點水平長度,a2為動臂桿長,a3為斗桿桿長,a4為鏟斗桿長,c234=cos(θ2+θ3+θ4),s234=sin(θ2+θ3+θ4)等。以挖掘機整平作業為例,實際中要求鏟斗相對設定直線軌跡以固定的切削角進行工作。如圖3所示,θd為固定切削角,θb為鏟斗齒尖與銷軸的連線與切削板的夾角,則鏟斗位姿角φ表示為:
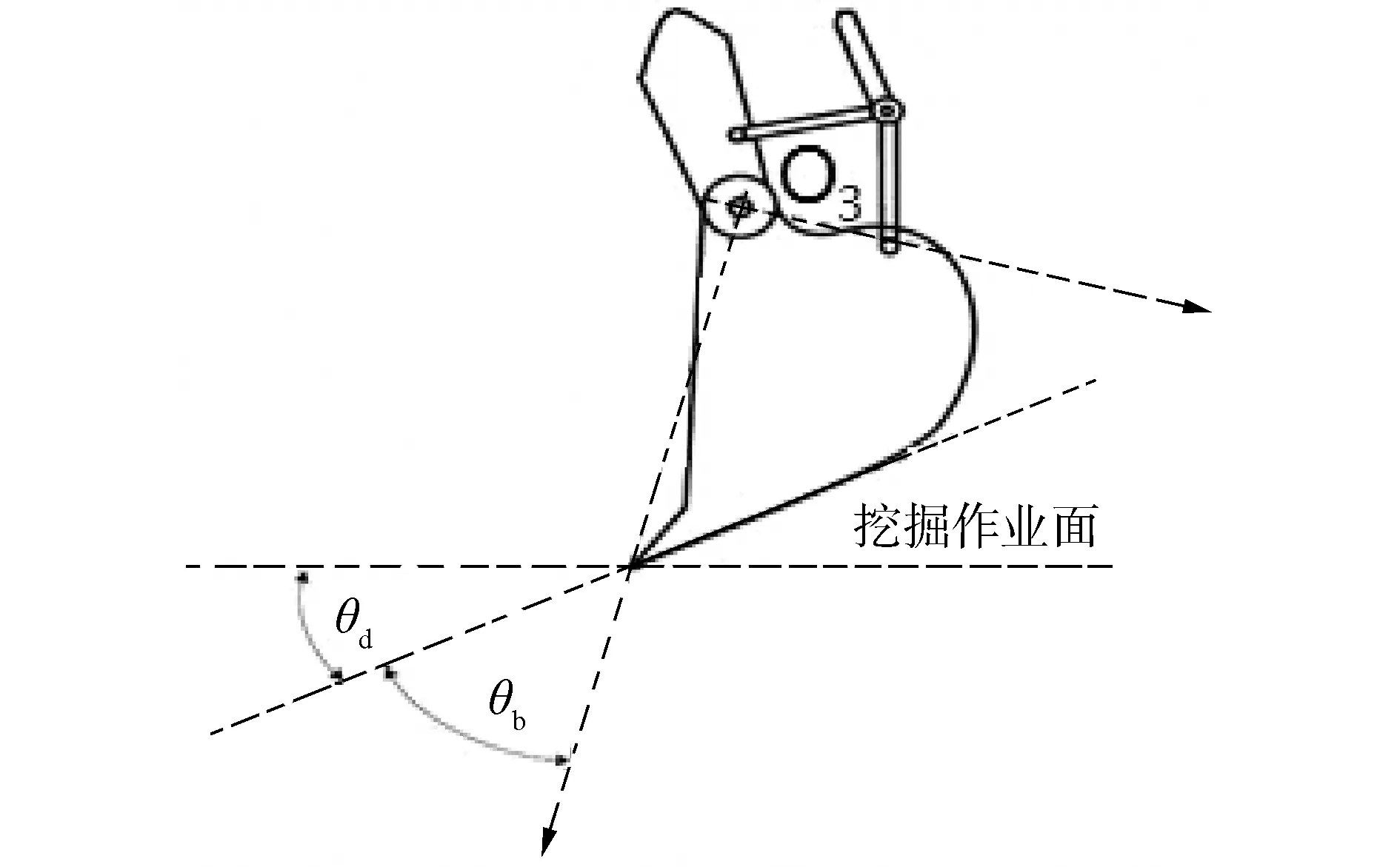
圖3 挖掘機整平作業鏟斗位姿Fig.3 The bucket posture of the excavator during straight-line motion
φ=θ2+θ3+θ4=θd+θb-π
(5)
即φ為固定值。
采用速度規劃曲線[21]
(6)
在水平作業面,以切削角θb=π/6進行整平作業(鏟斗斗尖從機身遠端移動至近端),由幾何關系式:
(7)
得到研究對象挖掘機動臂、斗桿與鏟斗關節空間角度規劃曲線及相應液壓缸桿軌跡規劃曲線,結果如圖4所示。
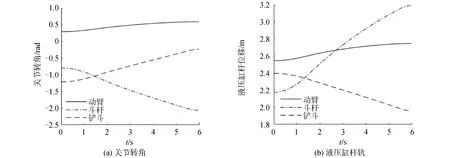
圖4 挖掘機作業面為水平面時的規劃曲線Fig.4 Excavator planning curves with horizontal working surface
2 閥控非對稱液壓缸數學模型
根據文獻[22],對挖掘機進行電液比例改造,圖5為改造后斗桿閥控非對稱液壓缸結構框圖。PS與PT分別為液壓泵供油壓力與回油壓力,UV為電磁閥閥芯位移,xp=lBD為斗桿活塞桿長度,QA與QB分別表示流入非對稱缸無桿腔的流量與流出有桿腔的流量,PA、AA與VA分別表示無桿腔壓力,活塞面積與容積。PB、AB與VB則表示有桿腔壓力,活塞面積與容積。
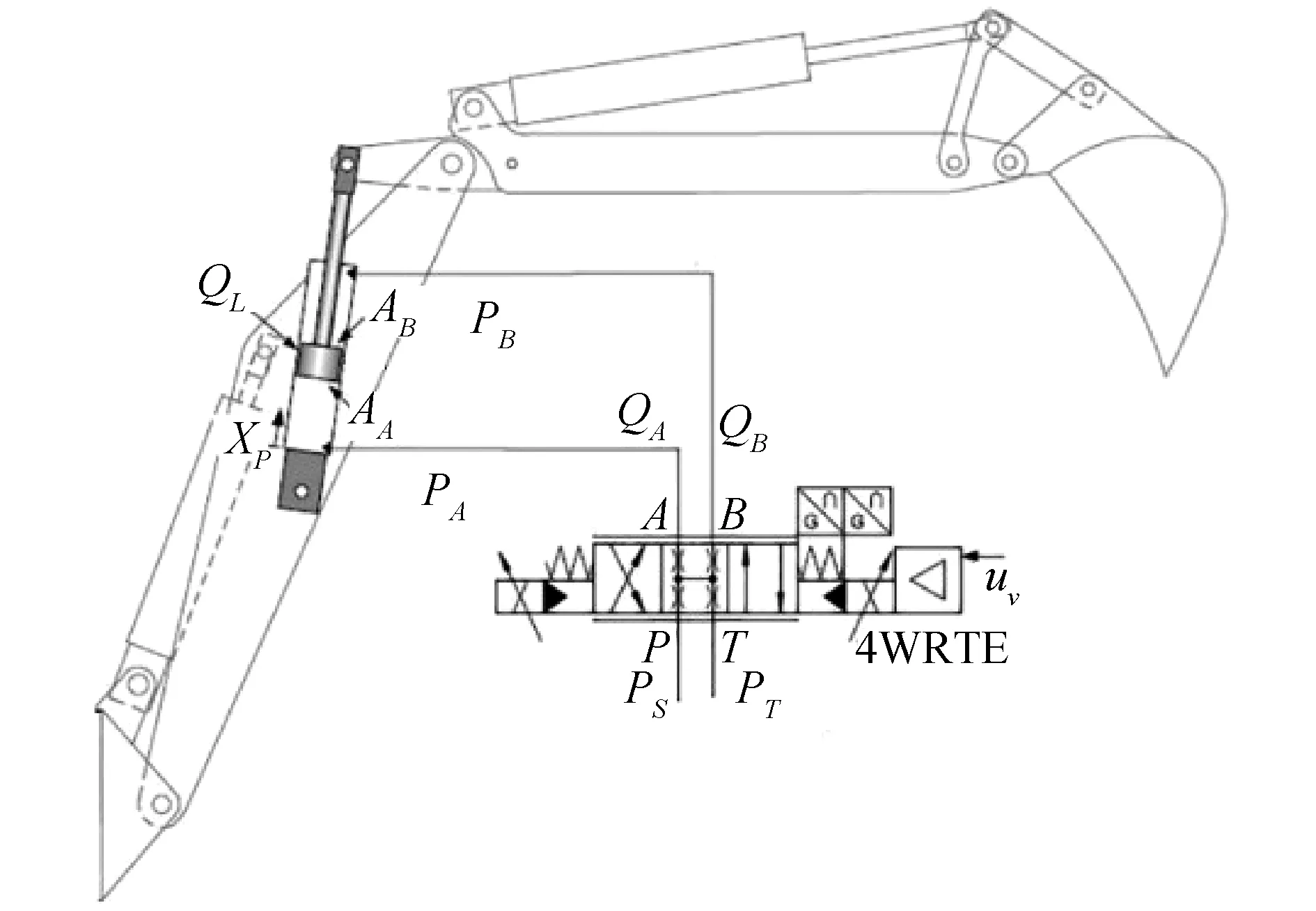
圖5 斗桿液壓系統Fig.5 The schematic of the stick cylinder system
斗桿液壓缸力平衡方程為:
(8)
式中:m為活塞桿及腔內液體等效質量;c為活塞桿粘性阻尼系數;k為活塞桿剛度系數。FBD為式(2)中對應于斗桿的驅動力分量。挖掘機在水平作業面按照規劃速度整平作業,考慮自重影響不計斗尖阻力時,FBD理論計算結果如圖6。
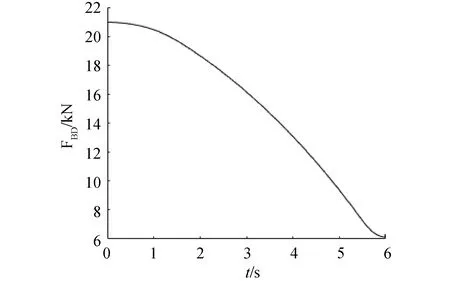
圖6 FBD的理論值Fig.6 Nominal value of FBD
斗桿閥控非對稱液壓缸在不考慮泄露因素條件下的流量連續性方程為:
(9)
式中:VA=VA0+AAxp為無桿腔容積,VB=VB0-ABxp有桿腔容積,VA0與VB0為各腔初始容積,β為液壓油液彈性模量。閥的節流方程:
(10)
式中h1與h2為流量增益系數。根據比例伺服閥特性曲線,流量QA和QB與伺服閥輸入電壓Vin的關系可線性化表示為[23]:
(11)
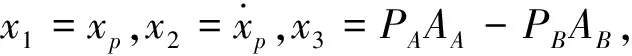
(12)
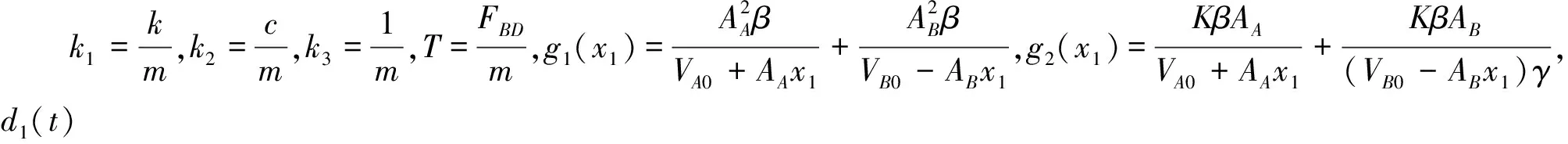
3 基于觀測器的滑模變結構控制
3.1 滑模高增益狀態觀測器設計
以斗桿液壓缸活塞桿軌跡控制為例,挖掘機在水平作業面整平作業時,采用規劃速度曲線得到的斗桿液壓缸活塞桿規劃軌跡如圖4(b)點劃線所示。為了降低控制成本,減少傳感器使用數量,僅使用位移傳感器測量活塞桿實際長度,采用高增益觀測器對其他控制狀態變量進行觀測。為對非匹配不確定項d1(t)補償,定義狀態變量:
(13)
則式(12)轉換為:
(14)
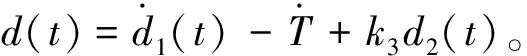
(15)
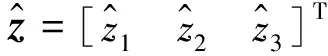
(16)
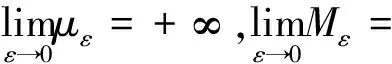
3.2 滑模控制器設計
根據滑模變結構理論定義滑模面:
(17)
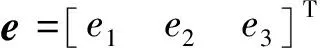
(18)
設計控制輸入u為:
(19)
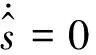
(20)
3.3 閉環系統穩定性
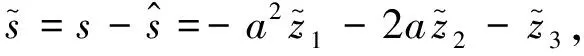
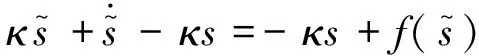
(21)

(22)
則狀態變量η與s可表示為奇異攝動標準形式:
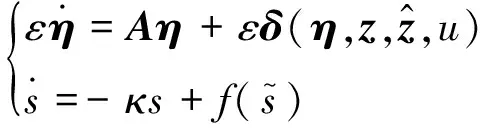
(23)
式中:η為快變子系統狀態變量;s為慢變子系統狀態變量,且

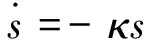
(24)
定義李雅普諾夫函數:
(25)
則有:
(26)
易知V指數收斂,且在有限時間內V=0?s=0,
(27)
因為Ae為Hurwitz,則跟蹤誤差e有限時間指數收斂。將式(23)時間尺度變換為τ=t/ε,則系統變換為:
(28)
當ε→0,式(28)表示為:
(29)
因為A是Hurwitz,存在正定矩陣Pη使得:
ATPη+PηA=-I
(30)
定義李雅普諾夫函數為:
Vη=ηTPηη
(31)
則其對時間尺度τ的微分:
(32)
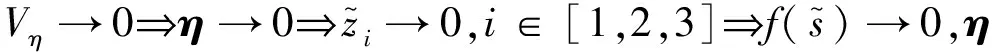
3.4 仿真

d(t)=(-89.1t4+1142.16t3-4 805.82t2+
7 149.8t+157.09)/160+100cos(2t)+
100sin(5t)/160
(33)

3 574.90t2-157.09t+20 816.56)/160


圖7 κ=100時ε對觀測誤差的影響Fig.7 The state estimation errors of high-gain observer with κ=100
由圖7易知,在不考慮系統噪聲環境下,ε值越小,對非匹配不確定項與匹配不確定項補償效果越好,觀測誤差越小。由圖8和圖9,κ值越大,閉環系統收斂越快。
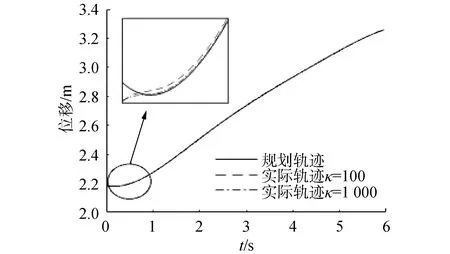
圖8 ε=0.001不同κ值的軌跡跟蹤效果Fig.8 The tracking performance of the HOSMC with ε=0.001

圖9 ε=0.001時不同κ值的軌跡跟蹤誤差Fig.9 The tracking error of the HOSMC with ε=0.001
4 結論
1)通過建立挖掘機關節空間與驅動空間關系,以液壓缸桿規劃曲線為跟蹤目標,伺服閥輸入電壓為控制輸入,使控制方式更加直接,易于實踐。
2)以斗桿活塞桿軌跡控制為例,采用高增益觀測器減少了傳感器使用數量,降低了控制成本。觀測器只需設計增益帶寬ε,設計參數少,方法更為簡便。在滑模控制中,通過對輸入切換項的符號函數采用滑模面函數代替,消除了抖振。閉環系統通過奇異攝動理論驗證了穩定性,跟蹤誤差有限時間收斂。
3)對于式(12)型的一類系統,通過定義新的狀態變量,采用基于高增益觀測器的滑模控制時,可選擇較小的帶寬參數ε與較大的κ值,滿足控制需要。對于挖掘機其他液壓缸的控制,在進行流量分配后,可類似斗桿液壓缸系統進行分析控制。

