基于內波統計特性的聲速剖面預測方法

蘇林， 孫炳文， 胡濤， 任群言， 王文博， 郭圣明， 馬力

(1.中國科學院聲學研究所 中國科學院水聲環境特性重點實驗室，北京 100190； 2.中國科學院大學，北京 100049)

海洋中的聲速剖面是影響水聲裝備性能的重要因素之一，決定了海洋中的聲傳播特性。海洋內波是廣泛存在于近海大陸架的一種中尺度海洋現象，在夏季，由于海水沿重力方向的溫度分布不均勻，海水中會形成一定的密度分層[1]。內波活動使海水的聲速分布產生劇烈變化，嚴重影響水下聲場分布[2-3]，進而干擾水下聲場預報效能[4]，特別是夏季有溫躍層時，若聲速擾動改變了躍層的斜率，可使聲波向下折射到海底進而影響探測作用距離[5]，因此聲速剖面的實時監測非常重要，為了預先了解區域聲場分布，對聲速剖面的預報更有實用價值。

海水聲速與溫度、鹽度和靜壓力有關，隨溫度、鹽度、壓力的增加而增加，其中以溫度的影響最為顯著，同時，溫度的變化也是最為顯著的，通常可通過現場監測的溫度數據和聲速經驗公式計算得到聲速剖面分布。聲速剖面具有明顯的深度分布，常表示為深度和聲速的矩陣數組，涉及參數量較大，即便在淺海環境也給聲速剖面的預報帶來很多困難，為簡化表達，提出了經驗正交函數(EOF)的方法[6]，基函數確定后，用有限的幾階系數即可重構聲速剖面，可以大大降低所需要的參數。Gaelle[7]在對意大利墨西拿海峽區域的內波分布研究中，指出可以利用2個EOF系數散點分布圖的統計特性監測內波，利用該特征可以進一步的降低聲速剖面預報所需參數，提升預報效率。

目前海溫預報主要方式有經驗預報方法、統計預報方法[8]和數值預報方法。其中經驗預報方法與人的主觀因素有很大關系；數值預報運算量極大，在要求預報時效性的基礎上對計算環境要求較高，且在初始場構建及物理過程參數化等方面有待完善；統計方法則是利用以往歷史數據或在線的實時、準實時數據，通過概率統計的方法計算預報未來海水溫度的變化規律。卡爾曼濾波方法是以統計理論為基礎的代表性同化方法，現在已逐漸應用到海洋數值模擬和預報中[9]，但卡爾曼濾波方法在狀態空間建模時仍需要較為準確的狀態方程描述海洋變化過程。神經網絡具有較好的自學習能力，可跳過復雜的海洋模型，直接從歷史及在線數據中挖掘內在聯系，尤其近年來海洋預報數據量驟增，積累了大量的潛浮標監測數據，均為神經網絡在海洋預報中的應用[10-11]提供了有力支撐。長短時記憶循環神經網絡(LSTM)[12]能有效利用時間序列數據中長距離依賴信息的能力，非常適合海洋溫度、聲速等時間序列的預測[13]。

本文深入挖掘了有無內波情形下時序聲速剖面所呈現的不同統計特征，結合LSTM對長時間序列的記憶功能，通過深度學習中神經網絡的方法學習歷史水文數據的變化規律，對淺海典型水文現象影響下的聲速剖面變化進行實時預測。

1 淺海內波環境下的聲速剖面統計特征分析

1.1 南海試驗概況

2019年9月，中科院聲學所水聲環境特性重點實驗室在中國南海海域組織了海洋調查試驗，試驗海區地形如圖1所示，海深約85 m，試驗期間在沿等深線方向布放了2套溫度鏈潛標，西側站位記為B站位，東側站位記為O站位。

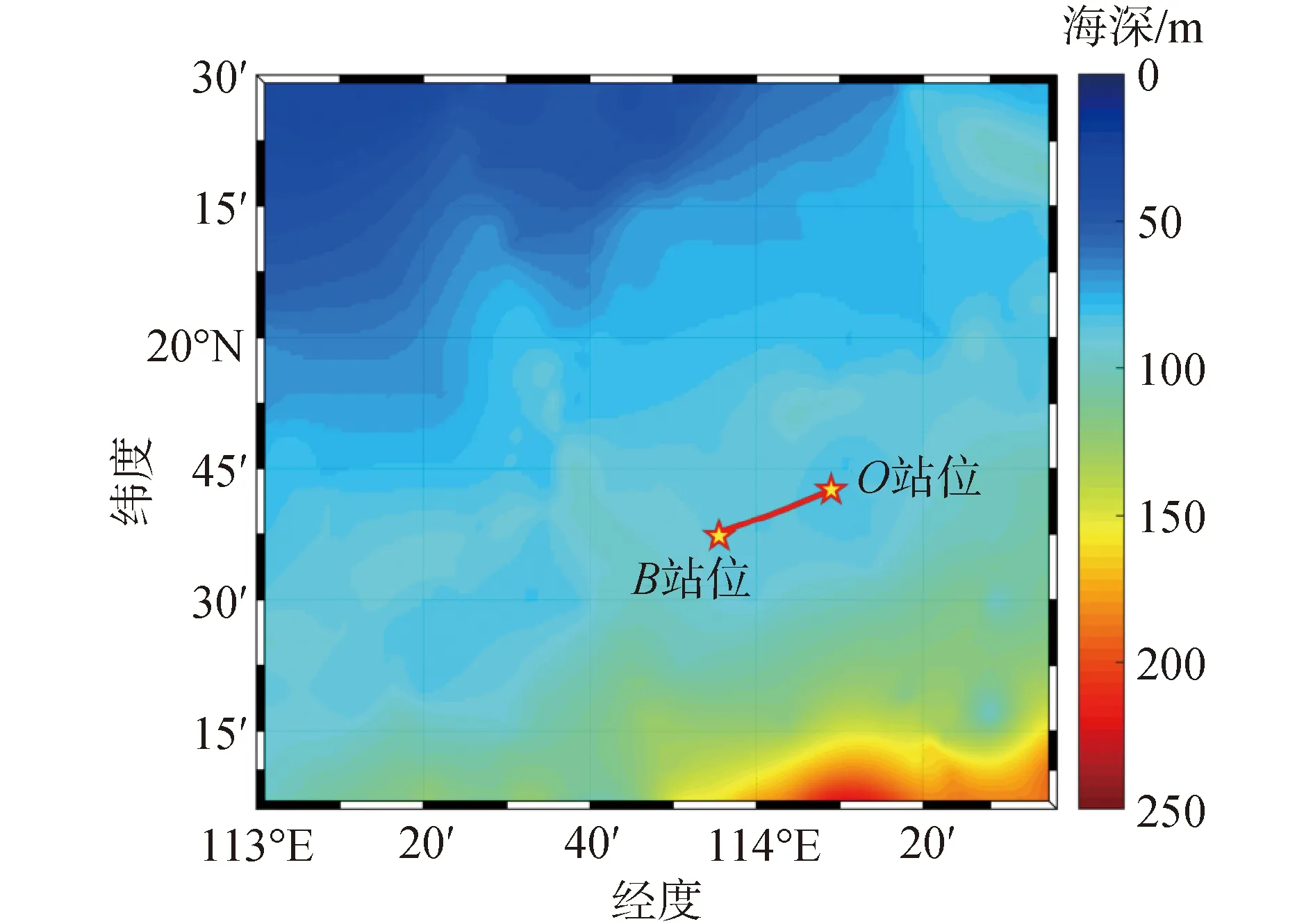
圖1 南海試驗地形Fig.1 Bathymetry of the experiment area in South China Sea

試驗從9月8日持續到9月15日，共采集到約171 h的溫度數據，如圖2所示，在整個試驗周期內可以觀測到豐富的內波活動，僅在8、9日2 d可觀察到明顯的半日潮，之后受到多源內波的影響，2個站位的溫度數據均出現無規律起伏，甚至覆蓋掉半日潮的大周期。提取2個站位的25 ℃等溫線及其包絡如圖3所示，從等溫線包絡線可以觀察到，在試驗初期2個站位的等溫線變化趨勢基本一致，之后出現較大差異，2個站位的25°等溫線深度相差高達20 m，推測試驗期間不僅存在B-O方向的內波，試驗后期還在O站位出現了垂直等深線方向傳播的內波，由于未觀測到更大空間范圍的溫度變化情況，對于內波的運動方向和速度尚不能確定。

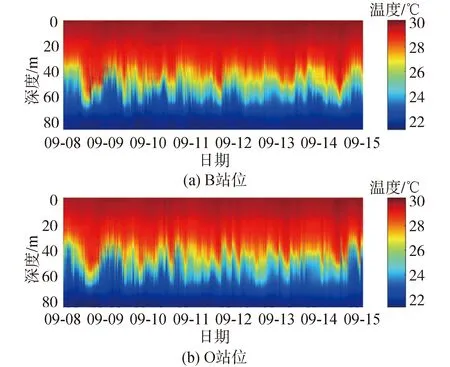
圖2 9月8日-9月15日連續水文監測數據Fig.2 Thermistor string measured temperature from Sep 8th to Sep 15th

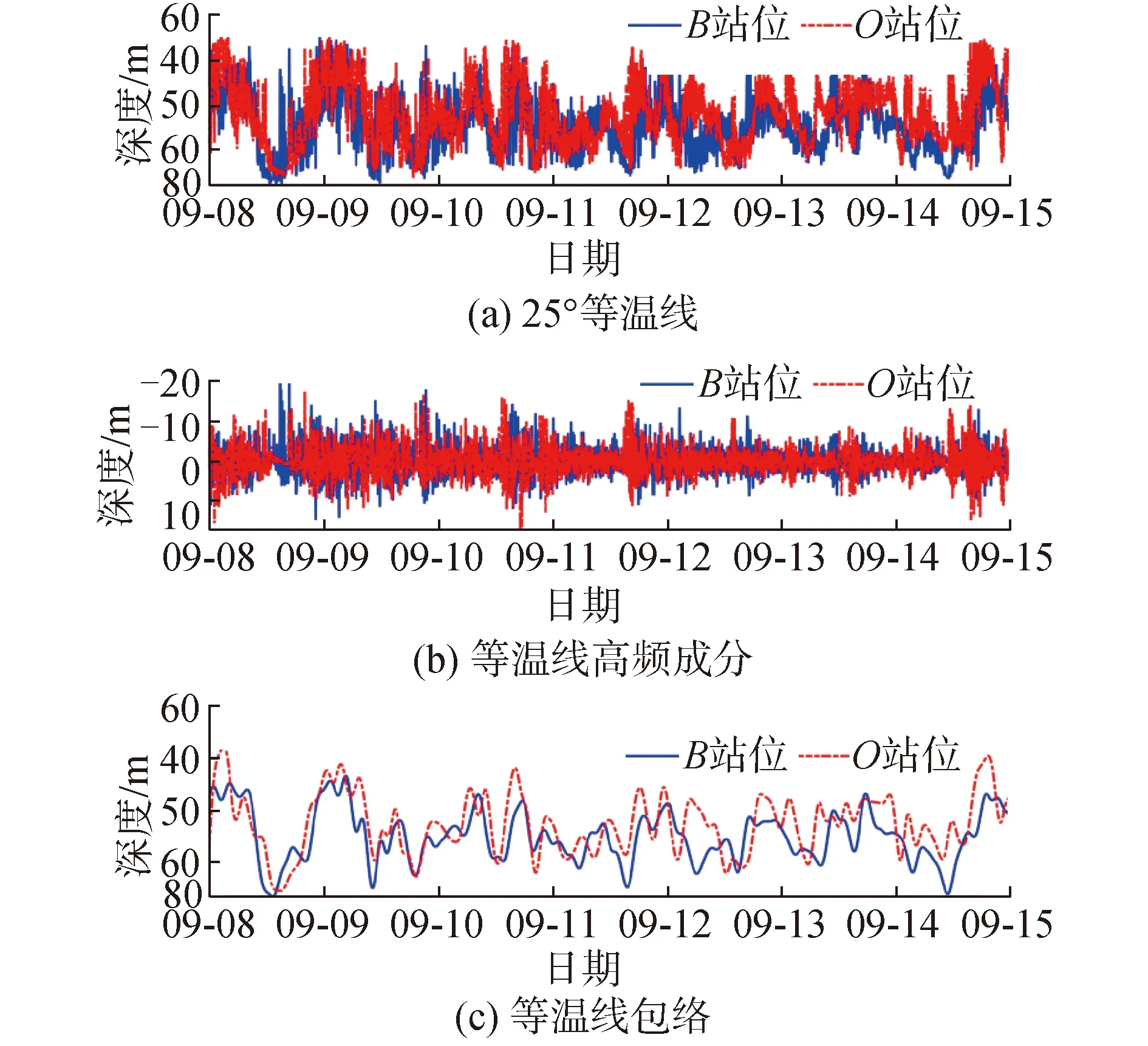
圖3 B站位和O站位25 ℃等溫線分布Fig.3 The 25 ℃ temperature contour of station B and station O

試驗中采用CTD測量得到了全海深的溫鹽深數據，如圖4所示。目前已經建立了許多利用溫度、鹽度和深度來計算聲速的經驗公式，為方便，采用Mackenzie[14]給出的9項算法，利用現場CTD測量得到的鹽度數據代入經驗公式，可將圖2中的溫度數據轉化為聲速數據，二者變化趨勢基本一致：

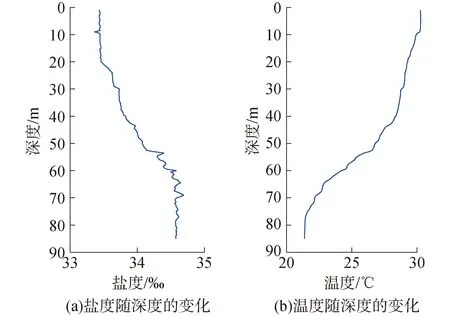
圖4 CTD測量得到的溫度和鹽度隨深度的變化Fig.4 The temperature and salinity data measured by CTD

c=1 448.96+4.591T-5.304×10-2T2+

2.374×10-4T2+1.340(S-35)+1.630×

10-2D+1.675×10-7D2-1.025×

10-2T(S-35)-7.139×10-13TD3

(1)

1.2 淺水聲速剖面的經驗正交函數表示

利用EOF方法表示聲速剖面可以大大降低聲速剖面預報所需要的參數個數，基函數確定后，用有限的幾階系數即可進行重構。

根據一段時間內測量到的N條SSP數據，可通過求平均值的辦法得到背景聲速剖面：

(2)

則聲速起伏可表示為：

(3)

設每條剖面離散到M個深度上，則N個Δc1(z)可以組成一個M×N的聲速起伏矩陣：

(4)

求得C的協方差矩陣：

(5)

對矩陣R進行特征值分解：

RU=Uλ

(6)

(7)

式中：um為要提取的第m階經驗正交函數，將M個特征值λm降序排列，選取前d個特征值對應的特征向量用來表示聲速剖面：

(8)

式中αm為第m階EOF系數。

通常情況下，在掌握了背景聲速剖面數據并提取到EOF基函數后，式(8)就可以較為準確地描述聲速剖面。同理，也可以由聲速剖面、EOF基函數和背景聲速剖面數據計算得到對應的EOF系數。

1.3 試驗數據的統計特征分析

由1.1節的試驗數據初步分析可知，在試驗最后一段時間監測到了內波活動，因此選取試驗最后一天(9月15日)的聲速數據進行EOF分析，截取時間段為15日5∶00-15∶00，該時間段的聲速起伏變化如圖5所示，其中白色分割線劃分出了訓練集以及待預測的測試集，整個時間段內的聲速剖面集稱為全集。圖6為使用圖5中訓練集聲速數據和全集聲速數據得到的前2階EOF基函數和背景聲速剖面，二者形狀基本一致。分別利用2個站位分解得到的EOF基函數和背景聲速剖面計算得到O站位聲速剖面的EOF系數隨時間變化如圖7所示，2種方法得到的系數變化趨勢基本一致。從O站位剖面中任取一條進行重構，重構剖面與原始剖面吻合較好，說明在全集時間段內，聲速剖面基函數未發生較大變化，可使用訓練集提取的背景剖面和EOF基函數重構測試集聲速剖面而不產生系統偏差。

圖5 參與統計分析的聲速數據Fig.5 Sound speed data used for statistical analysis

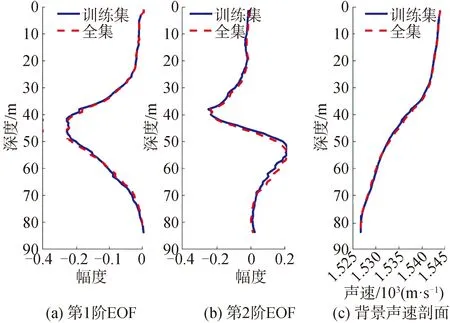
圖6 分別利用訓練集和全集聲速數據得到的前兩階EOF基函數和背景聲速Fig.6 The two first modes and the background sound speed profile extracted from training sets and complete sets respectively

對比圖7中第1階EOF系數與圖5中的溫躍層深度的變化規律，可以發現，二者變化趨勢基本一致，在溫躍層深度變化較大的時刻，第2階EOF系數較大，尤其在15日13∶00左右最為明顯。Gaelle曾在研究中給出了EOF系數的物理解釋[15]，第1階EOF系數α1表示了溫躍層的垂直位移，即α1越大則代表溫躍層越淺，躍層深度的變化周期也反映在α1的演化趨勢中，第2階EOF系數α2則表示了溫度梯度的改變，在溫躍層變化劇烈的時刻，α2取值也比較大。由此可推論，前兩階EOF系數之間并非完全獨立，二者取值存在某種內在聯系，即α2=f(α1)。

圖7 訓練集提取的EOF系數(9月15日)Fig.7 EOF coefficient extracted from the training set (sep.15)

將訓練集和測試集的前2階EOF系數分別繪制成散點圖如圖8所示，圖中散點對應EOF系數分布，實線是通過多項式擬合得到的曲線，訓練集和測試集數據均呈現出開口向上的拋物曲線分布，這與文獻[15]中墨西拿海峽試驗中得到的 “新月形”分布是一致的。圖8中同時給出了曲線擬合的一元二次多項式，且開口大小基本一致。圖9給出了2條擬合曲線的比較，在第1階EOF系數取值[-20, 40]，二者基本吻合，只在[-40，20]有偏差，最大偏差為4，由于第2階EOF基函數貢獻相對較小，認為這個偏差在可以容忍的范圍。對于沒有明顯內波存在的同時刻B站位聲速數據(見圖10)，EOF系數之間的統計特征則顯得雜亂無章，無法得到較精準的擬合曲線。這也進一步印證了可以從一段時間內EOF系數之間的統計特征來監測內波的存在。另一方面，可以將內波存在時的特殊統計模型作為先驗輸入，從而簡化聲速剖面的預測。

圖8 有內波存在時聲速數據的統計特征Fig.8 Statistical characterization of SSP in the presence of interval waves

圖9 訓練集和測試集擬合曲線比較Fig.9 Comparison of fitting curves of training and test sets

2 基于LSTM的聲速剖面預測

2.1 LSTM技術原理

循環神經網絡(RNN)是以序列數據為輸入，在序列演進方向進行遞歸且所有節點鏈式連接的遞歸神經網絡。因其具有記憶性、參數共享等特點，在對序列的非線性特征學習建模方面具有一定的優勢，被用于各類時間序列預報。然而RNN在處理時間序列上距離較遠的節點時會涉及到雅可比矩陣的多次相乘，帶來梯度消失或者梯度膨脹的問題。

LSTM是基于RNN 的一種完善，增加了記憶單元輸入門、輸出門和遺忘門等機制，網絡結構示意圖如圖11所示。各記憶單元內部運算機制為：

圖10 與圖5同時刻的B站位聲速數據的統計特征Fig.10 Statistical characterization of SSP of station B at the same time of Fig.5

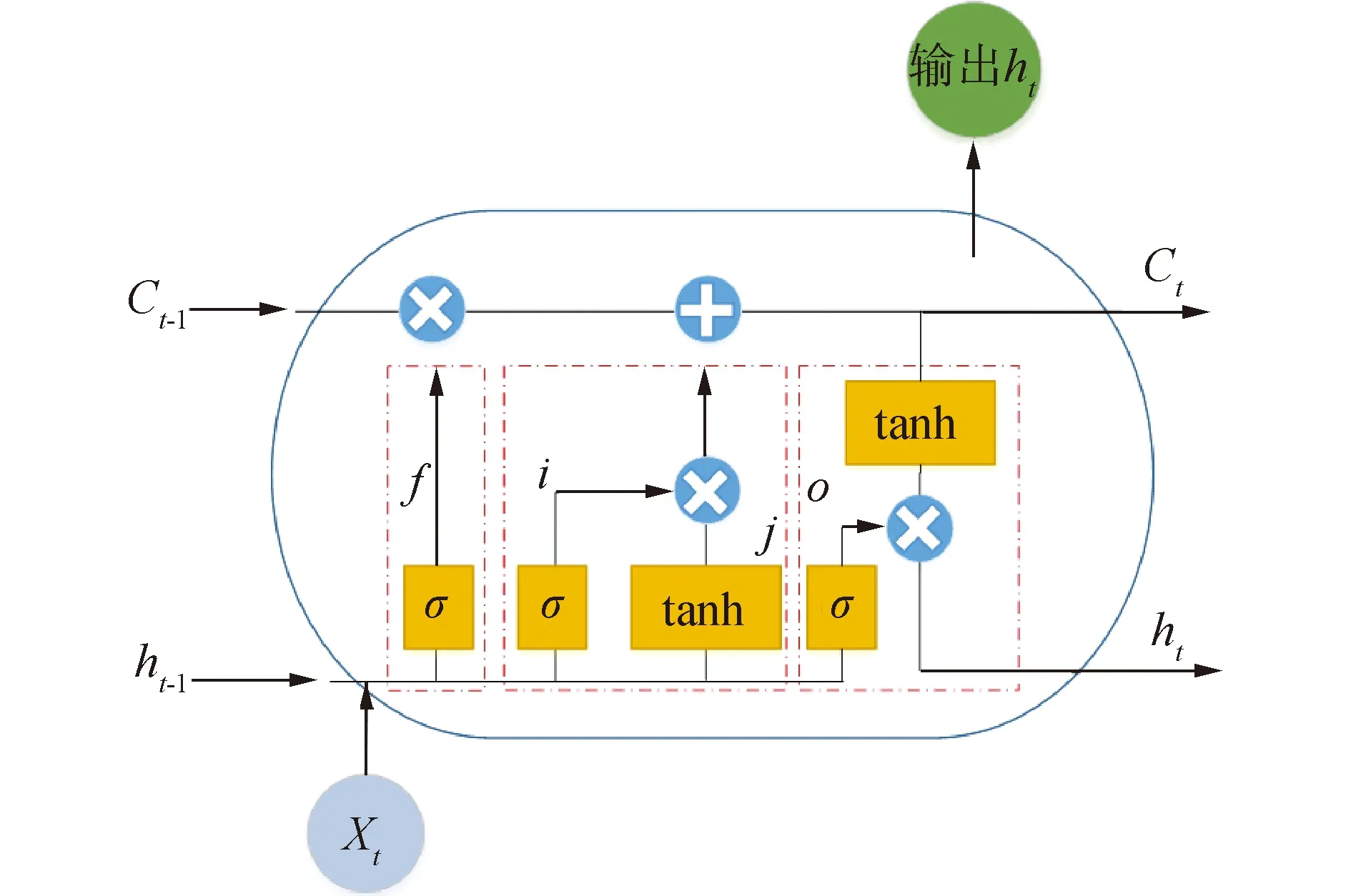
圖11 LSTM模型結構Fig.11 The schematic diagram of LSTM

(9)

式中：It、Ft和Ot分別代表輸入門、遺忘門和輸出門向量值；W1、W2和b分別表示輸入節點與隱藏節點、隱藏節點與輸出節點的連接權值以及對應的偏置項；xt對應t時刻的輸入；ht-1對應t-1時刻的輸出，代表了LSTM的隱藏狀態；σ為sigmoid激活函數，可將實數映射到[0,1]，1表示上一時刻單元的信息全部保留，0表示上一時刻單元的信息全部遺忘。這些“門”的結構實質上是使用sigmoid神經網絡與按位相乘結合，使用sigmoid作為激活函數的全連接神經網絡層會輸出一個0～1的數值描述當前通過該門的信息量，使得自循環的權重是變化的，避免了梯度消失等問題，可以控制不同時刻信息的傳遞來提升整個網絡對于長序列數據的處理能力。

2.2 試驗數據分析

考慮到內波統計特征，只將第1階EOF系數作為預測值，同時從訓練集提取的特征還包括EOF基函數、背景聲速剖面及內波統計特征。訓練集共包含7 h的聲速數據，從中提取第1階EOF系數并將數據預處理為具有零均值和單位方差的標準化數據，最終輸入LSTM網絡進行訓練，最大迭代次數為200，學習率設置為0.005，在150次迭代以后學習率降低為0.000 1，訓練在200代截至時已達到收斂，圖12為去標準化后的網絡輸出與實際測量值的比較，預測值變化趨勢與實際測量值基本一致，均方誤差為3.4，只在躍層深度劇烈變化的時刻，預測誤差略有增加。

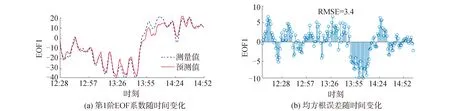
圖12 LSTM對第1階EOF系數網絡預測結果Fig.12 The first expansion coefficient predicted by LSTM model

利用內波統計特征和預測得到的第1階EOF系數即可計算得到第2階EOF系數的變化規律，如圖13所示，與測量值基本符合。進一步利用先驗EOF基函數和背景聲速剖面重構得到測試集聲速剖面如圖14所示，預測值與測量值基本一致，最大絕對誤差為3.69 m/s, 圖15為時間序列預測的均方根誤差(RMSE)，最大誤差為1.3 m/s。

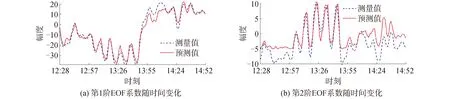
圖13 基于聲速剖面統計特征的LSTM網絡時前兩階EOF系數預測結果Fig.13 The two first expansion coefficients predicted by LSTM model based on the statistical characterization of SSP

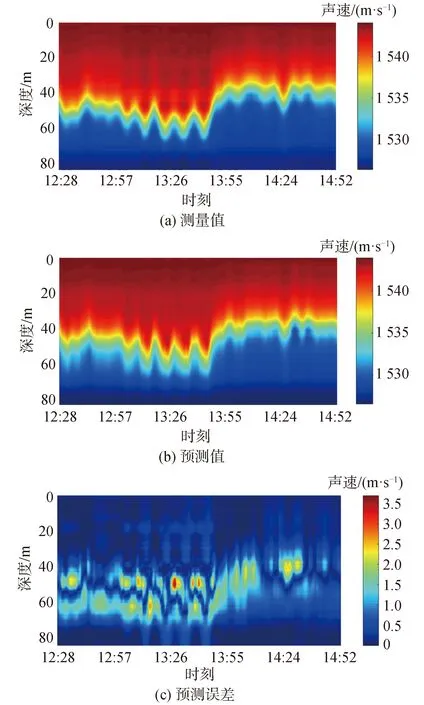
圖14 預測聲速剖面與測量聲速剖面對比Fig.14 Comparison of predicted SSP and measured SSP

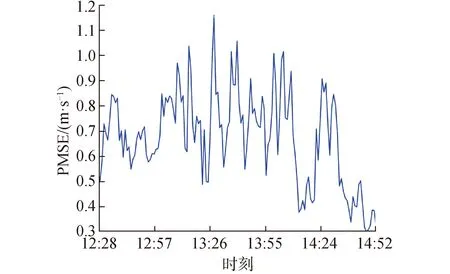
圖15 預測聲速剖面的均方誤差Fig.15 Mean square error of predicted SSP

值得說明的是，本文算法為簡化預測過程引入了內波統計模型，這同時也限制了其使用范圍，只在可觀測到明顯內波存在的時間段可實現聲速剖面快速實時預報。

3 結論

1)以南海實測聲速數據為基礎，深入挖掘了淺海環境中有無內波情形下的時序聲速剖面內在統計特征，根據提取到的前2階EOF系數α1、α2的變化趨勢與溫躍層深度變化規律，總結了有無內波情形下α1、α2的內在關聯關系和分布特征。

2)利用LSTM網絡對長序列的記憶功能，通過設計深度神經網絡對歷史聲速數據進行無監督特征學習，最后利用一段內波環境數據對訓練網絡進行驗證，聲速剖面預測結果與測量值符合較好。

綜上所述，融合內波統計特性和LSTM網絡模型的聲速剖面實時預報方法可跳過復雜的海洋模型，預先估計感興趣區域的聲速場分布特征。然而在實際海洋環境中，聲速剖面往往呈現出四維時空動態變化，水平非均勻變化也是影響聲場分布的重要因素，下一步工作將結合衛星遙感數據等更多樣的測量數據開展三維聲速場預報研究。

致謝：

本文研究成果得益于豐富寶貴的海試數據，特別感謝組織2019年9月南海試驗的胡濤、郭圣明老師以及參加試驗的同事和“實驗1”號全體船員。