具有非線性擴散的趨化模型弱解的有界性*

張婕燕， 辛 巧， 穆春來

1. 伊犁師范大學 數學與統計學院， 新疆 伊寧 835000； 2. 重慶大學 數學與統計學院， 重慶 401331

趨化行為是細胞沿化學物質濃度高的方向作的一種定向運動， 其研究在胚胎發育、 血管生成及種群動力學行為等方面具有重要意義． 文獻[1]建立了經典的生物趨化模型， 主要用于刻畫細胞對趨化—交叉擴散產生的奇異性反應的集體行為． 在過去的幾十年中， 經典的Keller-Segel模型解的存在性、 唯一性、 爆破行為及漸近行為等問題的研究得到了越來越多學者的關注， 取得了大量的研究成果[2-6]． 最簡單的Keller-Segel模型(記作KS模型)如下：

(1)

KS模型中的化學物質由細胞直接產生， 不同于該化學物質產生模式， 文獻[12]提出間接信號產出的生物趨化模型， 用于刻畫山松甲殼蟲的擴散和聚集行為． 關于間接信號產生的生物趨化模型， 主要集中研究帶有Logistic源的情形， 具體結果可以參考文獻[13-15]． 特別需要提到的是， 文獻[15]考慮具有擬線性擴散的生物模型， 其研究的擬線性擴散的生物趨化模型如下[15]：

(2)

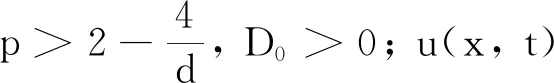
注1關于生物趨化模型(2)的弱解的定義可參考文獻[11]中定義1類似定義， 本文略．

注2當山松甲殼蟲的隨機布朗運動足夠強烈時， 即山松甲殼蟲的擴散強度超過甲蟲信息素對其的趨化吸引作用， 那么這個松林中山松甲殼蟲不會存在大量聚集現象， 不會對加拿大短葉松等松林造成了巨大的破壞． 如何增大山松甲殼蟲的擴散運動， 可能對于未來松林的保護具有重要的意義．

定理2設D(u)是具有C2光滑的非減函數， 趨化模型(2)存在弱解且v∈L∞(0，T；W2，∞(Ω))， 則趨化模型(2)的解必唯一．

1 趨化系統解的L∞估計

引理1[16]設v0∈W1，∞， 對所有t∈(0，T)， 都有‖w(t)‖Lq(Ω)≤C， 那么對任意t∈(0，T)和q∈[1，d)可得

‖v(t)‖W1， s≤C

(3)

其中

(4)

若q=d， 則對于任意的s<+∞， 都有(3)式成立； 若q>d， 則有‖v(t)‖W1，∞≤C．

此外， 考慮到擴散系數D(u)可能具有奇異性， 先考慮其正則性的趨化模型：

(5)

其中Dσ(u)=D(u+σ)且σ>0， 利用文獻[17]中Amann理論容易證明其局部適定性． 接下來， 先證明趨化系統(5)的解的全局適定性， 主要有如下引理．

‖u(t)‖Lq0≤C

證對趨化模型(5)的第三個方程兩邊同乘wq0-1， 然后在Ω上積分可得

(6)

進一步， 對(6)式的右端的最后一項用Young不等式可得

(7)

因為u的Lq0范數有界， 則聯合(6)和(7)式可知

(8)

其中C是常數， 即可知

‖w(t)‖Lq0≤C

因為

那么由Young不等式可知

和

另一方面， 對于?ε>0， 有

進而可知

(9)

首先假設q

(10)

其中b∈(0， 1)． 由于-Δ是D到L2(Ω)的同構映射(證明見文獻[16])， 其中

那么， 由Young不等式可知

整理可得

(11)

其中C是常數．

接下來， 對趨化系統(5)的第二個方程兩邊同乘-Δv， 然后在Ω上積分可得

由Young不等式可知

最后， 整理可得

(12)

對趨化模型(5)的第三個方程兩邊同乘w， 然后在Ω上積分可得

由Young不等式可得

整理得

(13)

聯合不等式(11)-(13)可知

(14)

1)在p+q>2時， 由Poincare不等式得

綜上所述可得

(15)

現在， 聯合不等式(14)和(15)可得

其中C(q)表示僅依賴于q的常數． 此外， 還有

(16)

和

這樣就可以得到

‖uε(t)‖Lq(Ω)≤C(q)

(17)

其中C表示僅依賴于q的常數與時間無關．

可知(17)式成立．

當q1≥d， 則由引理1可知， 對于任意的l<+∞， 都有‖v(t)‖Ll≤C， 易知(9)式右邊有界和(16)式成立， 那么對所有的q=q2

接下來， 可以利用文獻[11]引理3證明得到引理3， 利用文獻[18]引理4.1證明得到引理4．

引理3[11]假設定理1中所有條件成立， 則

‖v(t)‖L∞(Ω)≤C

(18)

引理4[18]設Ω?Rd(d≥1)是具有C1邊界的有界的開區域， 假設m>0，um>0， 對?u≥um， 使得D(u)≥m． 如果0

‖uε(t)‖L∞≤C2‖w(t)‖L∞≤C3

(19)

其中C1，C2和C3都是正數．

最后， 類似于文獻[11]的證明方法， 由σ的任意性， 可知解的收斂性． 此外， 上述推導出的所有估計值均不依賴于T， 因此趨化系統(2)弱解有界性是全局的， 可知定理1成立．

2 解的唯一性

本節利用能量方法來證明定理2即生物趨化模型(2)解的唯一性， 主要證明過程如下．

(20)

則可知

(21)

(22)

進而可得

(23)

接下來， 對(23)的右邊用Cauchy不等式得

和

此外可知

其中

進一步由方程(20)可知‖ψ(0)‖L2(Ω)=0． 進而可得：

最后可得

(24)

其中C是常數． 因此， 方程(24)等價于