變流速條件下非達西裂隙流溶質運移特征研究
李 旭,蘇世林,文 章,許光泉
(1.安徽理工大學地球與環境學院,安徽 淮南 232001;2.中國地質大學(武漢)環境學院,湖北 武漢 430078)
裂隙介質廣泛存在于自然界中,與人類的生產生活活動密切相關。裂隙介質中地下水滲流和溶質運移規律的研究一直是國內外學者重點關注的問題之一,但是由于裂隙介質具有強烈的空間變異性,使得溶質運移特性研究變得十分復雜[1-4]。近幾十年來,國內外學者對此開展了大量的研究,并取得了一定的研究進展,其主要研究成果可分為兩大類:第一類為裂隙網格中水流和溶質運移理論研究[5-6];第二類為單裂隙介質中水流和溶質運移理論研究[7-10]。單裂隙作為裂隙介質水流和溶質運移研究的基礎單元,多數研究通常是從單裂隙開始的。如鄭志成等[8]利用平行大理石板開展了單個裂隙溶質運移實驗研究,結果表明溶質的穿透曲線表現出拖尾的現象。因此,開展單裂隙溶質運移理論研究對于探索裂隙介質中溶質運移規律具有重要的理論意義。
通常情況下,單裂隙溶質運移理論研究主要是在達西流的基礎上進行的[11-12],然而越來越多的研究表明達西定律只在一定的水力梯度范圍內成立,裂隙介質中地下水流速過快往往會導致地下水滲流速度與水力梯度呈非線性關系,即所謂的非達西流[13-16]。Qian等[17]通過單裂隙室內實驗研究發現,單裂隙介質中地下水平均流速和水力梯度的關系能很好地與Izbash方程吻合,且水流速度與水力梯度的1/2次方成正比;李一鳴等[18]利用Izbash方程刻畫了單裂隙介質中的非達西流,研究當單裂隙的軸向與基巖水流方向斜交過程中,裂隙流的非達西程度對溶質羽分布的影響。上述研究表明,Izbash方程能夠很好地描述單裂隙介質中的非達西流,可以應用于單裂隙介質中溶質運移機理的研究。
目前國內外學者對單裂隙的非達西滲流和溶質運移開展了大量的理論研究,其研究通常假定地下水流是穩定的[19-21]。然而,實際裂隙含水層由于受到補給/排泄模式、地表水體水位以及區域地下水抽采率的變化等因素的影響,導致裂隙介質中地下水流速是隨時間發生變化的[22]。目前許多學者也開展了變流速條件下的溶質運移理論研究[22-24]。如Singh等[24]利用拉普拉斯變換得到了地下水流速為正弦變化的二維溶質運移的解析解;Li等[22]以松散含水層為研究對象,提出了指數變化的地下水流速方程,并利用積分變換獲得變流速淋濾作用下的一維溶質運移的解析解。目前關于變流速條件下的溶質運移理論研究對象主要為松散含水層,而裂隙含水層中的變流速溶質運移研究幾乎還是空白。此外,裂隙介質溶質運移過程中的地下水流時常不符合達西定律。因此,有必要開展變流速條件下非達西裂隙流溶質運移規律的研究。
為此,本文將建立變流速條件下考慮非達西流的單裂隙一維溶質運移模型。利用指數變化的地下水流速方程來刻畫單裂隙介質中地下水流速的變化規律,并耦合Izbash方程,利用積分變換的方法獲得變流速條件下單裂隙非達西流溶質運移的解析解,以此來探究非達西流和指數變化的地下水流速對裂隙介質中溶質運移的影響機理,以為裂隙地下水污染研究提供理論依據。
1 非達西滲流與變流速水流
1.1 裂隙達西流與非達西流
在裂隙介質中,當地下水流速較小時,黏滯力占主導地位,慣性力的影響可以忽略,通常用線性的達西定律來表示,即:
vd=-KJ
(1)
式中:vd為達西滲流速度[L/T];J為水力梯度[無量綱];K為裂隙介質的滲透系數[L/T]。
但當地下水流速較大、慣性力占主導地位時,地下水流速與水力梯度之間不再呈現線性的關系,發生非達西滲流。為此,國內外學者提出了不同類型的非線性流方程,在方程中因參數太多,限制了其應用[13]。本文采用Izbash方程來描述裂隙介質中的非達西滲流[18],其數學表達式為
vn=-kJ
(2)
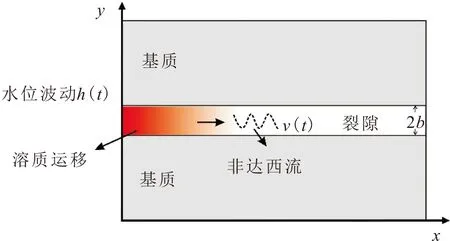
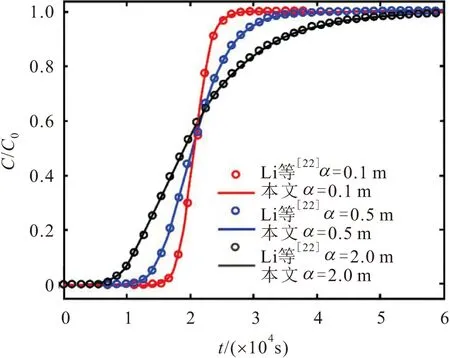
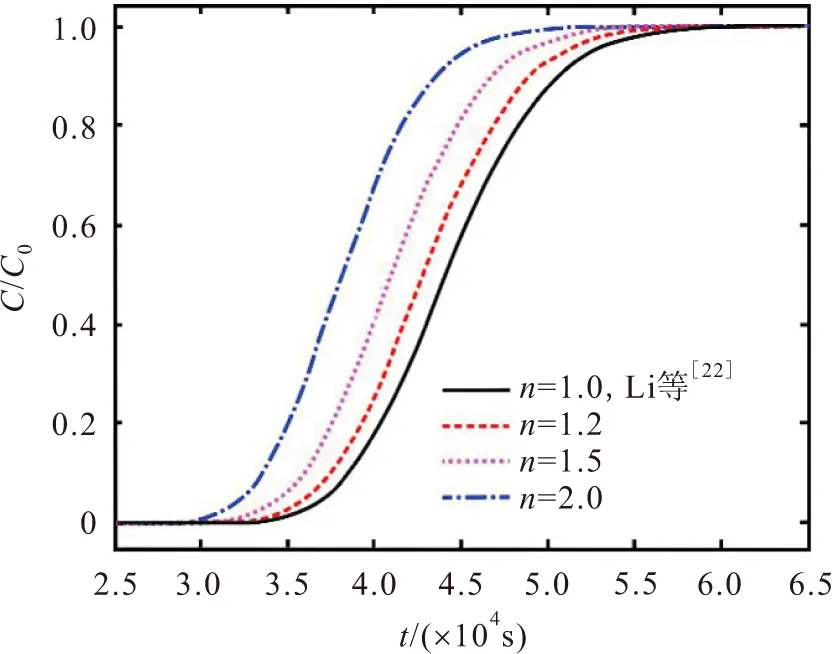
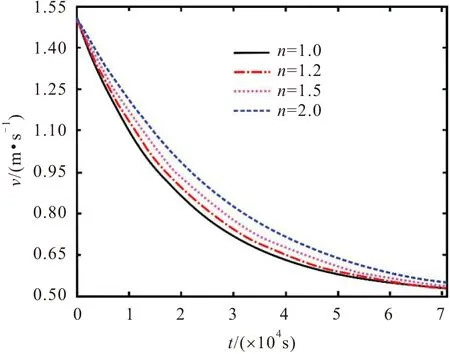
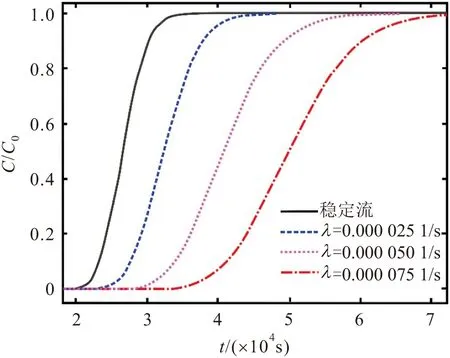
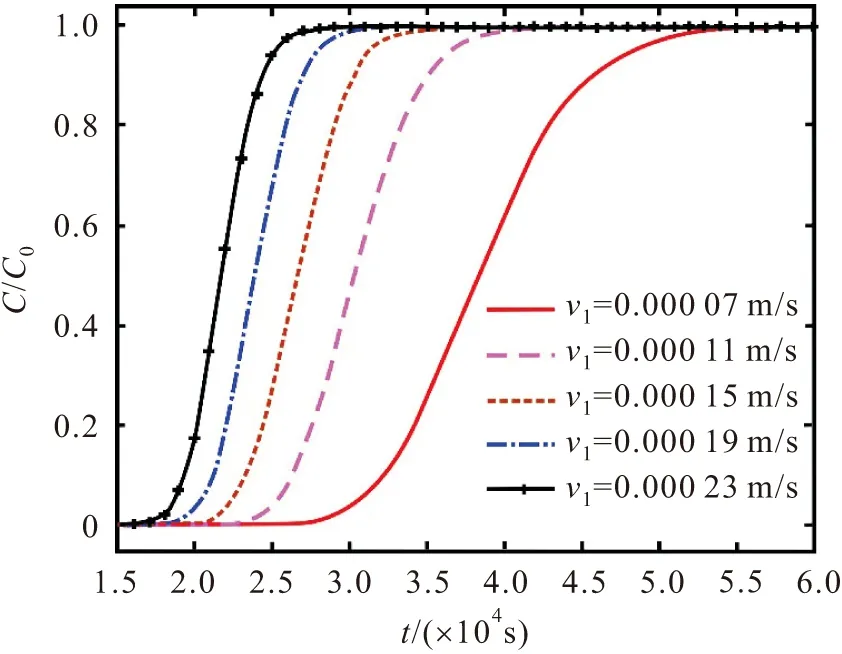
式中:n為經驗系數,n值反映了裂隙水流流態的變化,即從達西流(n=1)到非達西流(1 裂隙水流動狀態依據雷諾數(Re)判定,其判定方程為 (3) 式中:2b為裂隙的平均開度[L];q為裂隙介質中地下水平均流速[L/T];μ為地下水動力黏度[L2/T]。 通常情況下,裂隙中水流的Re大于1~10之間的某個值時,地下水滲流速度與水力梯度之間不再呈現線性的關系,而表現出非達西滲流的現象。 目前關于裂隙介質溶質運移模型中地下水流速通常設定為常數,但實際過程中地下水流速是隨著時間的變化而發生變化的(見圖1),針對這一問題,提出了采用線性方程和指數變化的方程來刻畫地下水流速的變化規律。實際上裂隙介質中地下水流速的變化應趨于某一確定的值,表現出指數增加或指數衰減的趨勢[22]。例如,當含水層受到生物、化學及物理的堵塞會導致其滲透性減小,使得含水層中地下水流速表現出指數衰減[25-26]。再如,河岸帶及海岸帶的裂隙含水層由于地表水位的波動(如洪水、潮汐等作用)也會引起含水層中地下水流速呈現出指數增加或指數衰減的趨勢[23]。因此,在達西流條件下的裂隙含水層中地下水流速可以表示為指數增加或指數衰減的形式[22]: 圖1 變流速條件下非達西裂隙流溶質運移示意圖Fig.1 Schematic diagram of solute transport under Non-Darcian flow and variable flow velocity in the fracture vd(t)=vd0φ(t)=vd1+(vd0-vd1)(e-λt) (4) 式中:vd0為單裂隙介質中初始的地下水流速[L/T];vd1為單裂隙介質中最終穩定的地下水流速[L/T];λ為地下水流速變化指數[1/T]。 當vd0>vd1時,公式(4)表示地下水流速為指數衰減的情況;當vd0 [v(t)]n=[v0τ(t)]n=(v1)n+[(v0)n-(v1)n](e-λt) (5) 式中:v0為非達西流條件下單裂隙介質中初始的地下水流速[L/T];v1為非達西流條件下最終穩定的地下水流速[L/T]。 若n=1時,公式(5)與公式(4)相同,則τ(t)可表示為 (6) 在建立變流速條件下非達西裂隙流一維溶質運移模型之前,為了簡化數學模型,假設條件為:①裂隙為單裂隙,其水流為非達西一維流動;②裂隙的開度不隨距離變化而變化,不考慮裂隙的粗糙度及充填物等因素的影響;③地下水流為非穩定流,其流速隨時間呈指數變化;④溶質為惰性溶質。則單裂隙介質中對流-彌散方程(ADE)可以表示為 (7) 式中:C為單裂隙介質中溶質的濃度[M/L3];x為距離[L];t為時間[T];D(t)為隨時間變化的彌散系數[L2/T],v(t)為隨時間變化的地下水流速[L/T],兩者分別表示如下: v(t)=v0τ(t) D(t)=αv(t)=αv0τ(t)=D0τ(t) (8) 式中:α為彌散度[L]。 將公式(8)代入到公式(7)中,可得: (9) 初始條件和邊界條件可表示如下: C(r,0)=0,x<0 (10) C(0,t)=C0,t>0 (11) C(∞,t)=0,t>0 (12) 式中:C0為x=0處給定的溶質濃度[M/L3]。 為了獲取模型的解,這里引入一個新的積分變換: (13) 則公式(9)可以表示為 (14) 邊界條件和初始條件在相同的積分變化下可以表示如下: C(x,0)=0,x<0 (15) C(0,T)=C0,T>0 (16) C(∞,T)=0,T>0 (17) 通過積分變換,公式(13)~(16)為經典的ADE模型。因此,一維半無限長單裂隙介質在x-T域中定濃度邊界條件下ADE模型的解為 (18) 式中:erfc(·)為余誤差函數。 將公式(13)代入到公式(17)中,可獲得一維半無限長單裂隙介質在x-t域中定濃度邊界條件下ADE模型的解為 (19) 上述推導的公式(19)為變流速條件下非達西裂隙流溶質運移模型的解析解。為了進一步驗證該模型的準確性,將不考慮非達西流的溶質運移結果,將本文模型解析解與Li等[22]的模型解析解進行了對比。Li等[22]提出了指數變化的地下水流速方程,并獲得了變流速條件下一維溶質運移模型的解析解,但是該模型沒有考慮非達西流的影響。當非達西參數n=1時,本文模型解析解結果應該與Li等[22]模型解析解結果一致。圖2為本文與Li等[22]模型解析解在x=20 m處的溶質穿透曲線(BTC)對比結果。模型主要參數設置如下:n=1,v0=1×10-3m/s,v1=6×10-3m/s,λ=0.000 01 1/s,α=0.1 m、0.5 m和2 m。 圖2 本文與Li等[22]模型解析解在x=20 m處的溶質 穿透曲線對比Fig.2 Comparison of the breakthrough curves at x=20 m computed by analytical solution of this study and Li et al.[22] 由圖2可見,本文模型解析解結果與Li等[22]模型解析解結果完全吻合,進一步說明本文的解析模型是準確的。 為了研究非達西流對單裂隙介質中溶質運移的影響,首先應確定非達西裂隙流地下水流速的范圍。本文將發生非達西流與達西流流態轉變的臨界雷諾數設定為10,由公式(3)可得到單裂隙介質中臨界地下水流速的計算公式為 (20) 將參數設置為:2b=0.02 m,μ=1.0×10-6m2/s[18],根據公式(20),可計算得到單裂隙介質中臨界地下水流速為0.000 5 m/s。 當裂隙介質中地下水流速為指數衰減條件下,在距離原始溶質注入點x=40 m處,當非達西參數n取不同值時的溶質穿透曲線,見圖3。模型主要參數設置如下:v0=0.001 5 m/s,v1=0.000 5 m/s,λ=0.000 05 1/s,α=0.1 m,n=1、1.2、1.5和2.0。 圖3 變流速條件下不同非達西參數n在x=40 m處 所對應的溶質穿透曲線Fig.3 Breakthrough curves for different Non-Darcian parameters (n) at x=40 m under variable flow velocity 由圖3可見,溶質穿透曲線的溶質濃度隨著非達西參數n的增大而不斷增大,表明非達西參數n越大,地下水紊流程度越高,溶質運移速度越快。 為了進一步分析導致溶質運移速度變快的原因,本文研究了不同非達西參數n時單裂隙介質中地下水流速v的變化,其變化曲線見圖4。 圖4 不同非達西參數n下單裂隙介質中地下水流 速的變化曲線Fig.4 Velocity curves of the groundwater flow in a single fracture for different Non-Darcian parameters (n) 由圖4可見,當裂隙介質中地下水流速由0.001 5 m/s減小到0.000 5 m/s時,非達西參數n越大,地下水流速衰減得越慢,地下水流速越快。總之,在變流速條件下裂隙介質中的溶質運移受到非達西流的影響明顯,非達西流的存在改變了裂隙介質中地下水流速的變化規律。因此,在裂隙介質中刻畫變流速溶質運移過程不能忽視非達西流因素的影響。 非達西流條件下地下水流速衰減指數λ取不同值時在x=40 m處所對應的溶質穿透曲線,見圖5。模型主要參數設置如下:v0=0.001 5 m/s,v1= 0.000 5 m/s,α=0.2 m,n=1.5,λ=0.000 025 1/s、0.000 050 1/s和0.000 075 1/s。對于指數衰減的地下水流速,λ值的大小反映了地下水流速衰減得快慢,主要是由地下水水位變化速率或者滲透性衰減得快慢所決定的。 圖5 非達西流條件下不同取值的地下水流速衰減指數 λ在x=40 m處所對應的溶質穿透曲線Fig.5 Breakthrough curves for different attenuation indexes λ of the exponentially decreasing groundwater velocity at x=40 m under Non-Darcian flow 由圖5可見,地下水流速衰減指數λ越大,溶質穿透曲線的溶質濃度越小,說明地下水流速衰減指數λ越大,溶質運移速度越慢。這主要是由于地下水流速衰減指數λ越大,地下水流速衰減得越快,導致溶質運移速度越慢。當v1=0.001 5 m/s時,地下水為穩定流,本文通過對比變流速條件下的溶質穿透曲線與穩定流的溶質穿透曲線可以發現,變流速條件下溶質穿透曲線的溶質濃度值均小于地下水穩定流的情況,說明地下水流速的變化對裂隙介質中溶質運移有較大的影響。 非達西流條件下地下水流速v1取不同值時在x=40 m處所對應的溶質穿透曲線,見圖6。模型主要參數設置如下:v0=0.001 5 m/s,λ=0.000 050 1/s,α=0.2 m,n=1.5,v1=0.000 7 m/s、0.001 1 m/s、0.001 5 m/s、0.001 9 m/s和0.002 3 m/s。當地下水流速v1取不同值時,公式(2)可以表示為地下水流速指數增加或指數衰減的函數形式。因此,當v1>0.001 5 m/s 時,地下水流速為指數增加的函數形式;當v1<0.001 5 m/s 時,地下水流速為指數衰減的形式;當v1=0.001 5 m/s 時,地下水為穩定流。 圖6 非達西流條件下不同v1取值在x=40 m處所 對應的溶質穿透曲線Fig.6 Breakthrough curves for different final steady velocities (v1) at x=40 m under Non-Darcian flow 由圖6可見,地下水流速v1越小,地下水流速衰減的幅度越大,溶質穿透曲線的溶質濃度越小,溶質運移速度越慢。例如,當v1=0.000 7 m/s時,溶質運移速度最慢,其溶質穿透曲線位于最右端(見圖6)。另外,地下水流速v1越大,地下水流速增加的幅度越大,溶質穿透曲線的溶質濃度越大,溶質運移速度越快。因此,利用公式(2)可以刻畫裂隙介質中地下水流速的指數增加或指數衰減的情況,為研究地下水流速變化對溶質運移的影響提供了有效途徑。 本文依據Izbash和指數變化的地下水流速方程建立了單裂隙介質非達西流溶質運移新模型,通過積分變換的方法得到了模型的解析解,并模擬分析了非達西流和指數變化的地下水流速對裂隙介質中溶質運移的影響,得到如下結論: (1) 變流速條件下,單裂隙介質中非達西參數n越大,地下水紊流越強,地下水流速越大,導致溶質運移速度越快,溶質穿透曲線的溶質濃度越高。因此,單裂隙介質中刻畫變流速溶質運移過程不能忽視非達西流因素的影響。 (2) 單裂隙介質中指數變化的地下水流速對溶質運移有較大的影響,地下水流速的衰減指數λ越大,地下水流速衰減得越快,溶質穿透曲線的溶質濃度越低,溶質運移速度越慢。 (3) 地下水流速(或漸進地下水流速)在單裂隙介質溶質運移過程中起到了關鍵的作用,其大小反映了地下水流速增加或減小的幅度,其變化的幅度越大,溶質運移速度快慢表現得越明顯。1.2 變流速水流
2 數學模型及求解
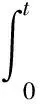
3 結果分析與討論
3.1 非達西裂隙流的溶質運移特征
3.2 變流速條件下非達西流裂隙流的溶質運移特征
4 結 論

