一種基于污染風險的地下水監測井網多目標優化方法

閆 聰，林斯杰，鄧澤政，楊 慶，劉明柱*

(1.中國地質大學(北京)水資源與環境學院，北京 100083；2.南方科技大學環境科學與工程學院，廣東 深圳 518055；3.北京市地質礦產勘察院，北京 100048)

地下水是維系地下水依賴型生態系統生態服務功能的核心資源，在干旱-半干旱地區顯著影響著植被動態和土壤水平衡。然而伴隨著經濟社會的不斷發展，很多地區地下水受到了嚴重污染，使地下水生態服務功能受到了不同程度的影響。地下水監測可為管理和保障地下水生態安全提供必要的信息。地下水污染監測井的科學布設是地下水保護工作的基礎，也是國內外地下水監測領域的共性難題。合理的地下水污染監測井布設是獲取有用的地下水污染信息的前提。合理地布設地下水污染監測井，可以大大降低相關監測成本，提高獲取信息的可靠性。開展地下水污染監測井網布設的優化研究，目的在于以最小的監測成本獲取空間和時間上最具有代表性的地下水水質信息。目前綜合考慮不確定性和定性風險評價的多目標優化技術被越來越多的學者采用，原因在于該技術同時考慮了多個目標，且優化方案是根據相互競爭的目標函數優先地位來排序的。多目標優化方法已逐步成為應用最廣泛的地下水污染監測井網布設優化技術。

區域地下水污染監測井網布設優化方法主要包括水文地質分析法和數理統計法。作為一種定性方法，水文地質分析法是地下水污染監測井網布設優化的基礎方法，該方法主要根據水文地質條件、人為活動、地下水價值等因素對地下水污染監測區域進行動態疊加和劃分，最終確定地下水污染監測井位置的合理性。常用的水文地質分析法有地下水動態類型編圖法和地下水污染風險編圖法，其中地下水污染風險編圖法主要適用于地下水污染監測井網布設的優化研究。而數理統計法作為定量方法，主要包括地統計法、主成分分析法、遺傳算法、模擬退火算法等，如Tamer等以用最少數量的監測井提供足夠空間覆蓋的地下水質量信息為目標，采用遺傳算法識別現有地下水污染監測井網絡中的冗余井，獲取了最佳的地下水污染監測井網布設方案。其中，地統計法較為常用，但多適用于針對地下水水位監測井網的單目標優化；主成分分析通過對多個指標的降維，可實現地下水污染監測井布設的優化，但該方法可能無法獲取最優解；遺傳算法適用于地下水水質監測井網的優化，通過尋求最優解可獲取最佳的地下水污染監測井網，但該方法計算耗時大；模擬退火算法同樣適用于地下水污染監測井網的多目標優化，且該方法計算效率高，但目前多應用于地下水水位監測井網的多目標優化。

鑒于此，本文在前人模擬退火算法的基礎上，利用隨機森林方法篩選出對地下水質量演化指示性最強的監測指標，并結合水文地質分析法，考慮地下水污染風險性，以監測成本最低、精度最高和不確定性最小為目標函數，建立了區域地下水污染監測井網多目標優化模型，最后通過案例應用，以驗證該方法的有效性。

1 研究方法

1.1 區域地下水污染監測井網多目標優化模型構建

對于人類生活聚集地，尤其是城市，需對地下水整體狀況進行長期監測，以便掌握地下水質量的時空變化過程，為地下水管理及維護地下水生態安全提供基礎信息，因此需建立以監測成本最低、監測精度最高和不確定性最小為目標函數的區域地下水污染監測井網多目標優化模型。其中，監測成本可用地下水污染監測井的數量表示；監測精度可用地下水污染監測井網的數據丟失量表示；不確定性可簡化為地下水污染監測井的均勻分布。該多目標優化模型目標函數的數學表達式如下：

min

F

=min

N

(1)

min

F

=min(CORR+DIST)

(2)

min

F

=minMSSD

(3)

式中：

F

表示地下水污染監測井的數量；

F

表示地下水污染監測井網的數據分布；

F

表示不確定性；

N

表示監測井的數量;CORR表示監測數據的相關性分布函數，DIST表示監測數據的邊際分布函數，CORR和DIST函數值越小，說明優化前后地下水污染監測井網的相關性分布越接近；MSSD表示地下水污染監測井距離均值，其值越小，說明地下水污染監測井分布越均勻，地下水污染監測井網的不確定性越低。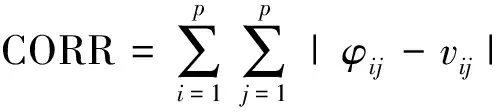

(

4

)

(

5

)

(

6

)

多目標優化是通過最小化

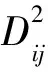
n

個目標函數，在每個目標函數的解空間中尋求最優解。為了求得最優解

S

,

本文采用加權求和法(Weighted Sum Method),該方法通過自定義每個目標函數的權重，將單個目標函數(Objection Function，OF)聚合為效用函數

U

(Utility Function)，即新的目標函數(OF):

(

7

)

然而，解決多目標優化問題時，每個目標函數具有不同的數量級和單位，在加權求和過程中，數量級較大的目標函數往往占有主導性，而遮蓋了其他目標函數，即權重的設定可能無法真實體現出目標函數的重要程度，因此需要采用函數轉換方法對每個目標函數進行標準化處理，具體處理方法如下:

(

8

)

1.2 區域地下水水質監測指示性指標篩選方法

地下水水質監測指標數量多、信息量大且存在冗余，而地下水污染監測井網優化模型結果的好壞往往在很大程度上取決于監測數據的質量。為了識別冗余信息，提高監測數據的質量，減少冗余監測指標對優化模型結果的影響，本文基于地下水質量評價結果，采用隨機森林算法識別對地下水水質具有重要指示性的監測指標，并將其作為后續地下水污染監測井網優化的指示性指標。

隨機森林(Random Forest，RF)算法是由Breiman等提出的，該方法結合了Bagging算法和隨機子空間算法，是一種分類預測算法，也是一種組成式的監督學習方法。RF算法在識別地下水水質監測指示性指標的過程中，具有以下優勢：

(1) 能夠充分利用地下水水質多年監測數據，通過大量長時間序列的數據建立預測模型。

(2) 可以較好地處理地下水水質監測數據缺失問題。

(3) 對于基于數值變量和因子變量所建立的地下水水質監測指示性指標重要性識別模型具有較高的準確性。

為了度量地下水水質監測指標的重要性，RF算法使用特征變量重要性進行度量，度量參數有OBB平均下降精度(Mean Decrease Accuracy，MDA)和基尼指數(Gini)。

MDA相當于均方誤差，是用于衡量某一指標的值取為隨機數時，RF算法預測準確性的降低程度，其值越大，表明指標的相對重要性越高。MDA的計算公式如下：

(

9

)

基尼指數(Gini)為數據集中隨機指標被分錯的概率，用來表示節點的純度，基尼指數越大，表明指標的相對重要性越高。基尼指數的計算公式如下：

(

10

)

式中：

p

表示數據集

D

中第

k

個指標所占的比例；

y

表示指標總數；Gini(

D

)表示數據集中隨機指標被分錯的概率。

1.3 區域地下水污染監測井網多目標優化模型求解方法

模擬退火(Simulated Annealing，SA)算法，也稱蒙特卡洛退火、統計冷卻或隨機松弛算法， Kirkpatrick等將該方法引入組合優化領域，旨在有效地解決最優解問題。SA算法是一種源于統計物理學的組合優化算法，已經廣泛應用于地統計模擬和優化空間采樣。

SA算法源于金屬原子退火，即金屬原子快速加熱，然后緩慢冷卻的過程。冷卻(退火)過程中，金屬內部原子發生改變，從而形成具有更低能量狀態的金屬原子網絡。在地下水污染監測井網多目標優化中，SA算法中的每個金屬原子對應著地下水監測井網中的單個監測井，整個系統的能量狀態代表監測井網優化過程中的目標函數。SA算法在求解地下水污染監測井網多目標優化模型中，具有如下明顯的優勢：

(1) 針對大量的地下水水質監測數據，能夠進行高效率的求解計算。

(2) 靈活性高，可以突破局部最優解，而到達全局最優解，即能夠對區域地下水監測井網進行整體優化，而非局部優化。

(3) 對于多目標優化問題，該方法允許用戶自定義目標函數。

SA算法的核心是需要求解優化的目標函數(金屬原子內能)。針對地下水污染監測井網多目標優化問題，SA算法求解優化目標函數的步驟如下：

第一步，需通過對

S

的隨機擾動產生新的目標函數φ

(S

+1

)

，從而形成多目標優化問題的解空間

S

。對于

S

+1新解是否接受，則依賴于概率接受準則，即Metropolis算法。當φ

(S

+1

)

≤φ

(S

)

時，則接受新解

(S

+1

)

；當φ

(S

+1

)>

φ

(S

)

時，則需要根據Metropolis算法判斷是否接受新解，見下式:

(

11

)

式中：

c

為退火溫度；

P

為接受概率。

對于復雜的多目標函數，局部最優點可能與全局最優點(最佳監測井網)存在很大的差異，這種情況下搜索過程會停止在局部最優點，而通過Metropolis算法，使SA算法具有從局部最優點逃逸而獲得全局最優點的能力。

第二步，在求解最佳監測井網時，需要設置相關參數，SA算法涉及的一組控制參數稱為退火時間表，其中重要的控制參數有初始溫度

C

、初始接受概率

P

、溫度降低因子(即退火速率)

α

等。退火速率采用最簡單也是最常用的退火方式，即指數式降溫，其關系式如下：

C

+1

=αC

(k=

1

,

2

,

…

,N)

(

12

)

式中：

k

表示馬爾可夫鏈(Markov chain)

;C

表示第

k

個馬爾可夫鏈的溫度；

C

+1表示第

k

+1個馬爾可夫鏈的溫度；

α

為退火速率，取值范圍為0.8～0.99，一般取0.95。

第三步，在模擬退火過程中，目標函數的迭代過程也需要終止條件，SA算法的退火終止條件有3個：

(1) 終止溫度:若干次迭代后，若

C

+1達到終止溫度(設定的閾值)，則迭代過程終止。(2) 目標函數

:

迭代過程中，目標函數在

N

次迭代中都保持不變或者變化很小時，迭代終止。

(3) 接受概率:當新解不優于當前解，通過Metropolis算法計算所得的概率低于接受概率，迭代終止。

SA算法計算過程簡單，通用性和魯棒性強，可用于求解復雜的非線性優化問題。相比于其他算法，作為交互式方法的SA算法的計算量更少，盡管它不能保證找到最優解，但是可以確保找到近似最優解。

2 案例應用研究

2.1 研究區概況

本文選擇北京市平谷盆地(116°55′～117°24′ E,40°01′～40°22′ N)為研究區。平谷盆地位于北京市東北部，西距北京市區70 km，東距天津市區90 km，面積約為340 km(見圖1)。區內主要有4個沖洪積扇，地勢東北高、西南低，按地貌形態分為侵蝕地貌、坡洪積地貌、沖洪積地貌，地層巖性主要有第四系砂礫巖、砂巖和基巖。平谷盆地含水層主要有4層，研究區中部和西北部有兩個地下水源地，水質良好。平谷盆地潛水含水層共布設了地下水污染監測井32口，其中污染源監測井19口(見圖1中灰色圓點)，主要分布在研究區西北部、北部和中部；區域地下水污染監測井13口(見圖1中黑色圓點)，較均勻地分布在平谷盆地內。

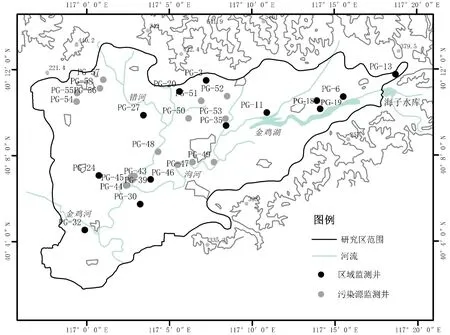
圖1 研究區現有地下水污染監測井網分布示意圖Fig.1 Overview of current groundwater pollution monitoring well network in the study area

2.2 地下水水質監測指示性指標篩選

地下水水質監測指示性指標篩選是地下水污染監測井網優化的關鍵，參與優化的指標不同，則地下水污染監測井網的優化結果也不同。為了評估地下水水質監測指示性指標篩選的合理性，本文對比分析了對地下水質量綜合評價法和隨機森林法的指標篩選結果。

2.2.1 地下水質量綜合評價法的指標篩選結果

圖2 研究區地下水質量評價指標的超標率Fig.2 Standard-exceeding rate of indicators for groundwater quality assessment

2.2.2 隨機森林算法的指標篩選結果

盡管通過地下水質量綜合評價法能夠識別出研究區地下水水質監測指示性指標，但體現不出其他常規指標的重要性。本文基于地下水質量綜合評價法的評估結果，采用隨機森林算法構建了區域地下水水質監測指示性指標重要性識別模型，以每個監測井的地下水水質評價等級作為預測變量，17個地下水水質監測指標作為樣本變量，共生成500棵傳統決策樹，最終得到每個監測指標的相對重要性排序結果，見圖3。

圖3 研究區地下水水質指標的相對重要性排序Fig.3 Ranking of relative importance of monitoring indicators of groundwater quality

2.3 地下水污染風險評價結果

地下水污染風險性越高，地下水被污染的概率就越大，監測井存在的必要性越大，監測井的密度/數量可適當提高/增加；相反,地下水污染風險性越低，地下水被污染的概率越小，監測井的密度/數量可適當降低/減少。

本文采用矩陣疊加法對研究區地下水污染風險性進行了評價，其評價結果見圖4。

由圖4可見，研究區王都莊、中橋水源地地下水污染風險集中在低和中等等級，沖洪積扇扇緣地下水污染風險等級為高、很高。

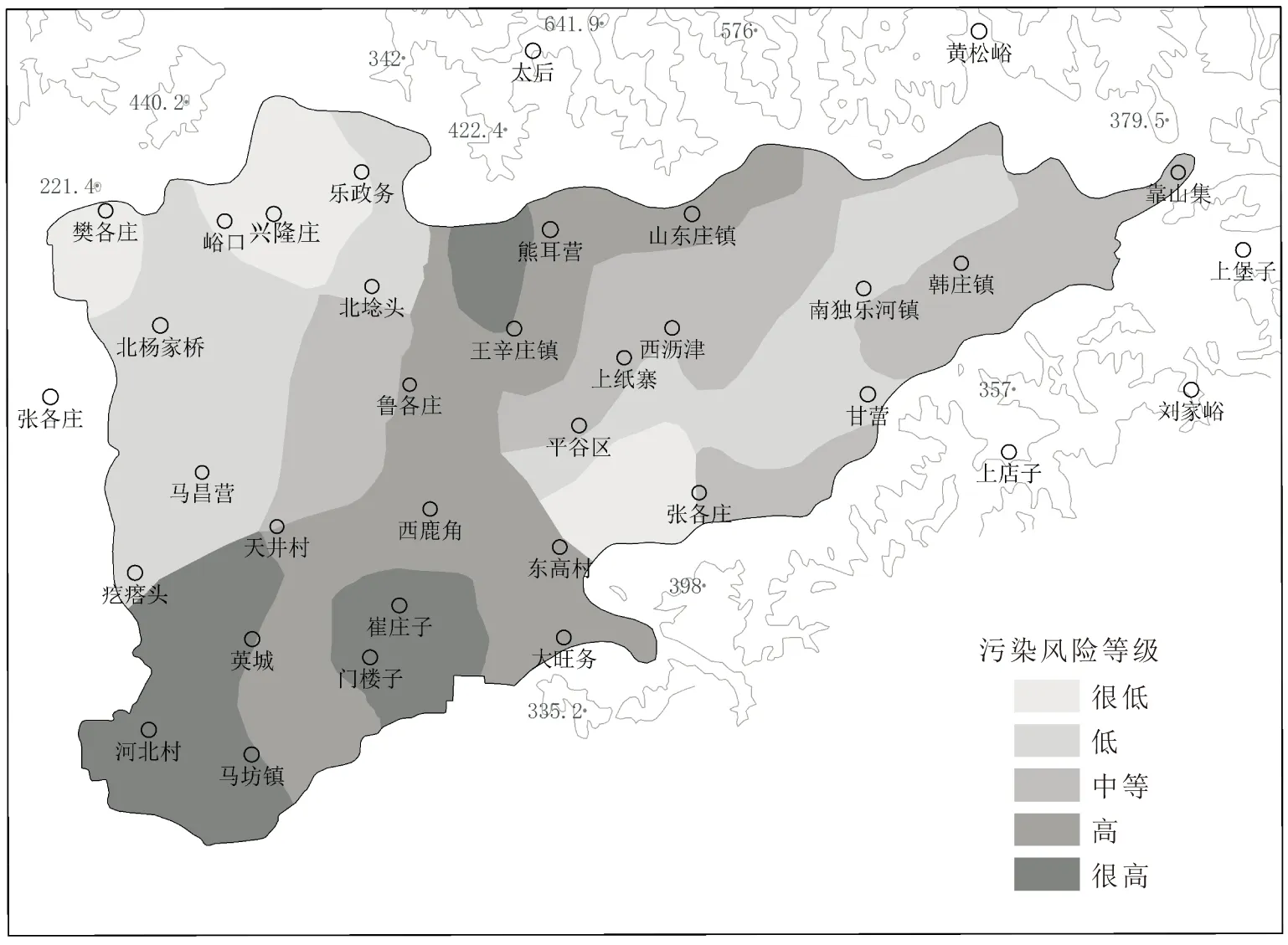
圖4 研究區地下水污染風險評價分區圖Fig.4 Zoning map of groundwater pollution risk assessment in the study area

2.4 區域地下水污染監測井網優化結果

2.4.1 多目標優化模型參數設置

模擬退火算法在退火過程中設置了相應的退火時間表，見表1。

表1 退火時間表Table 1 Parameters annealing schedule

加權求和法在聚合單個目標函數形成新的目標函數(OF)的過程中，需設置每個目標函數的權重，用以表示單個目標函數間的相對重要程度。則目標函數OF可表示為：OF=1/2 CORR+1/3 DIST+1/6 MSSD，其中CORR、DIST和MSSD的權重分別為1/2、1/3和1/6。

2.4.2 冗余監測井識別結果

在識別冗余監測井的過程中，首先需要確定冗余監測井的數量，根據目標函數值與監測井數量之間的關系曲線(見圖5)，可得出不同監測井數量最優的目標函數值。

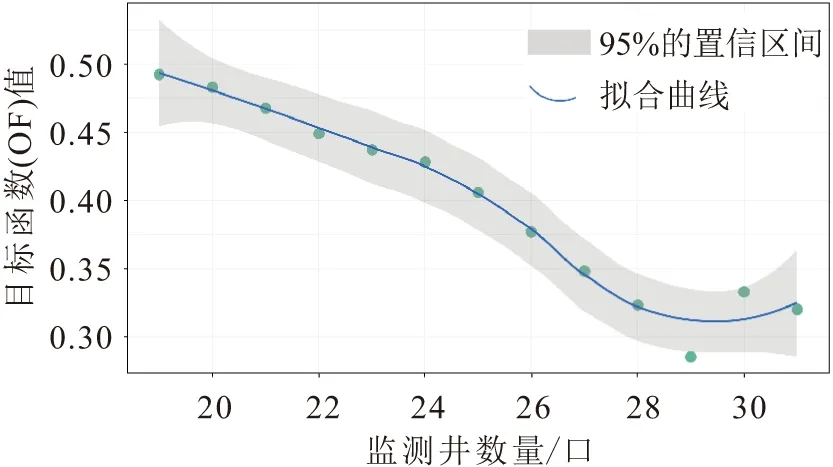
圖5 目標函數(OF)值與監測井數量的關系曲線Fig.5 Change curve of objective function with number of monitoring wells

由圖5可見，整體上目標函數(OF)值隨監測井數量的增加呈遞減趨勢，當監測井數量為29口時，OF值達到最低值，即CORR、DIST、MSSD多目標組合問題達到最優解；當監測井數量大于29口，OF值隨監測井數量的增加由遞減變為遞增趨勢，因此最優的監測井數量為29口。

通過上述方法求解多目標優化模型，優化過程中每個目標函數隨迭代次數的增加而遞減(見圖6)，當迭代次數為3 000次時，目標函數CORR、DIST、MSSD以及OF趨于穩定，其中OF值為0.375。

圖6 目標函數收斂圖Fig.6 Convergence of the objective function

本文識別出的研究區冗余監測井位置，見圖7。

圖7 研究區冗余監測井的識別結果Fig.7 Identification of redundant monitoring wells of the study area

由圖7可見，研究區地下水很高污染風險區有3個區域，每個區域都至少存在1口監測井，分別為PG-20、PG-30、PG-32；研究區3口冗余監測井分別為PG-18、PG-47、PG-58(見圖7中紫色圓圈)，其中PG-18為區域監測井，地下水污染風險等級為低，PG-47和PG-58為污染源監測井，地下水污染風險等級為低和很低，因此3口冗余監測井都位于地下水低污染風險區。

表2 研究區冗余監測井的N-N濃度估計精度Table 2 Estimation accuracy test of N-N concentrationin redutant monitoring wells

2.4.3 新增監測井預設方案

研究區內某些地區缺乏地下水監測井，如馬昌營、夏各莊等地區，造成區域內地下水信息不確定性較大，因此需要在這些區域內增加新的監測井。但新的監測井缺乏地理信息和監測信息，并且含水層的邊界不規則且變化幅度大，而MSSD函數可以較好地解決這一問題，該函數可降低地下水污染監測井網的不確定性，形成分布更為均勻的地下水污染監測井網。在缺乏地理信息的情況下，首先通過GIS隨機在區域內生成300個監測點，以隨機監測點作為新增監測井的候選點；然后通過模擬退火算法建立目標函數MSSD的地下水污染監測井網優化模型，其迭代計算過程見圖8。

圖8 MSSD目標函數的迭代計算過程Fig.8 MSSD function iterative

地下水污染監測井網的監測精度隨監測井數量的增加而提高，監測成本也隨之增加。本文為了提高地下水污染的監測精度，在研究區內新增了5口監測井，研究區地下水污染監測井網優化后的點位分布見圖9。

圖9 研究區地下水污染監測井網優化后的點位分布圖Fig.9 New scheme after optimizing for monitoring well network

由圖9可見，地下水污染監測井點均勻分布在平谷盆地內，其中地下水污染很高風險區內新增1口監測井，地下水污染高風險區內新增2口監測井。

3 結 論

(1) 針對地下水水質監測指標信息量大而存在冗余的問題，采用隨機森林算法篩選出對地下水質量具有重要指示性的監測指標。

(2) 結合水文地質分析法和模擬退火算法，基于地下水水質監測指示性指標的識別結果，提出了以監測成本最低、監測精度最高、不確定性最小為目標函數的多目標組合優化模型，為識別冗余監測井和新增監測井提供參考，實現了以最低成本的地下水污染監測井網獲取最多地下水信息的目的。

(3) 平谷盆地案例應用研究表明：基于設有32口井的初始監測井網，運用模擬退火算法求解多目標優化模型，得到每個目標函數和效用函數的Pareto最優解，并綜合考慮研究區地下水污染風險性的評價結果，得到優化后研究區地下水污染監測井數量為29口，識別出冗余監測井3口，再通過普通克里金法分析了3口冗余監測井的合理性，最終保留PG-47監測井，去除PG-18和PG-58監測井。此外，針對研究區內部分區域監測井不足的情況，提出了新增監測井的預設方案。