基于滲透率修正因子的氣體有效擴散系數分形模型

王昌進，張 賽，徐靜磊

（昆明理工大學機電工程學院，昆明 650500）

0 引言

多孔介質中的氣體擴散問題是能源開采、燃料電池、化學工程等領域研究的重點，但是氣體在多孔介質中的擴散包含了很多復雜的傳質機理，如何建立多孔介質中氣體有效擴散系數模型成為研究熱點［1］。

傳統的物質擴散定律一般由菲克定律來描述，該定律描述了物質擴散通量與濃度梯度之間的定量關系。Cao 等［2］通過建立多孔介質三維模型，證明在穩態情況下，菲克定律能夠在多孔介質氣體擴散中適用，然而該模型使用的是100×100×100 的立方網絡模型，對于多孔介質的不規則性和復雜性方面的描述不夠準確。氣體在多孔介質中復雜的輸運機理與多孔介質孔隙大小和結構差異有很大關系，根據多孔介質孔隙大小和結構的不同，多孔介質中的氣體流動與擴散常常劃分為4 個流動區域：連續介質區、滑移區、過渡區和自由分子區［3］。Beskok等［4］通過大量實驗給出了一維圓管中氣體體積流量的表達式，該表達式引入克努森數kn和滲透率修正因子f（kn），可以適用于所有流動區域。符東宇等［5］運用格子Boltzmann 方法研究了頁巖氣藏的滲流規律，發現克努森數kn是影響頁巖氣滲流的主要參數。Roy 等［6］使用Ar，N2，O2和Al2O3作為實驗材料進行了擴散實驗，引入了克努森擴散系數，建立了微納米孔道中的氣體擴散方程，但是該方程只能適用于自由分子區。張烈輝等［7］考慮了多重運移機制，建立了頁巖氣藏的綜合滲流模型。李亞雄等［8］通過研究頁巖氣的滑脫和擴散機理，提出了“壁聯擴散”的新概念來表征克努森擴散和表面擴散的總效應，但該方法的數學模型與論證過程還有待完善。在一些科學研究和實際情況中，例如川南地區頁巖孔隙結構和川西坳陷致密砂巖孔隙結構，它們的孔道直徑很小，達到了微納米級別，此時，孔隙結構顯示出分形的特性。陳居凱等［9］，朱漢卿等［10］和鄧浩陽等［11］均使用分形理論研究了頁巖與致密砂巖等致密多孔介質的孔隙結構。目前，也有很多文獻將分形理論運用到氣體滲透和擴散中［12-14］。Zheng等［15］基于分形理論和毛細管束模型，得到了氣體的有效擴散系數模型。該模型能與已有實驗數據相吻合，并且能適用于不同的多孔介質。Shi 等［16］在考慮了2 種運輸機制的情況下，運用分形理論建立了H2在燃料電池氣體擴散層中的有效擴散系數模型，并且分析了分形理論相關參數（孔隙度、分形維數等）的影響。Zhang［17］考慮了3 種多孔介質中的氣體流動機理，得到了滲透率和氣體有效擴散分形模型，但忽略了氣體的滑脫效應。Woignier 等［18］研究了分形多孔介質中氣體在滑移區的擴散機理并建立了滑移模型。張賽等［19］和牟新竹等［20］在研究多尺度分形多孔介質氣體擴散時加入了孔隙連通性參數，得到了新的數學模型。以上研究大多只考慮了1 種或2 種氣體擴散機理，不能完整地描述氣體在多孔介質中的擴散問題。

基于Beskok 等［4］給出的表達式、迂曲毛細管束模型、分形理論和菲克定律，建立氣體在多孔介質中擴散的分形模型；該模型包含面積分形維數、迂曲分形維數、孔隙度、最大最小孔隙直徑、氣體密度、黏度、摩爾質量等參數，然后分析這些參數與氣體有效擴散系數之間的函數關系與變化趨勢，以期能夠正確地描述氣體在多孔介質中的擴散規律，并應用于油氣田的開發。

1 多孔介質的分形特征

1.1 孔隙數目與橫截面積描述

在具有分形特性的多孔介質中，孔隙直徑大于等于λ的孔隙數量的總和與孔隙直徑大小滿足下面的分形標度關系［21］

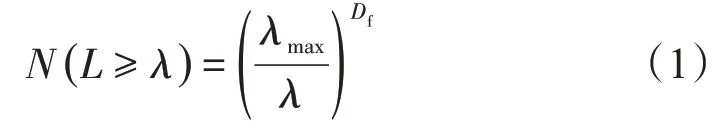
式中：N為孔隙長度大于孔隙直徑的多孔介質的孔隙總數目；L為毛細管長度，m；λmax與λ分別為最大孔隙直徑和孔隙直徑，m；Df為無因式多孔介質的面積分形維數。

在真實多孔介質中，孔隙數目十分巨大，根據統計理論和方法，可以將式（1）看成是連續和可微的函數，對式（1）進行微分可以得到

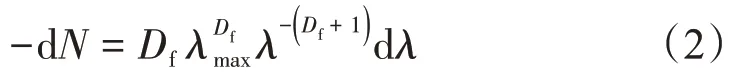
式（2）得到了在(λ,λ+dλ) 的孔隙數目，表明了孔隙數目隨著孔隙直徑的增大而減少，-dN＞0。由于截面上的孔隙可以看作是直徑不同的圓，因此通過式（2），用微元法可得到分形集中截面上總的孔隙面積AP為

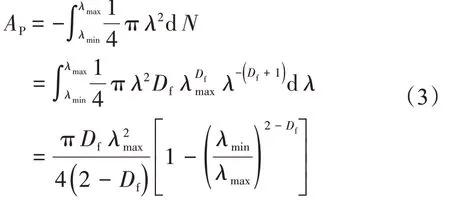
式中：AP為截面上的總的孔隙面積，m2；λmin為最小孔隙直徑，m。

則總的截面積At可以計算得到

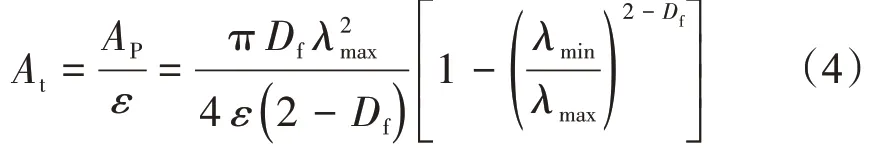
式中：At為總的截面積，m2；ε為面孔隙度。

一般情況下，體孔隙度和面孔隙度不相等，兩者之間相差一個迂曲度因子

式中：Φ為體孔隙度；為迂曲度因子［1］。在計算多孔介質相關參數時通常使用的是體孔隙度，通過式（5）可以實現面孔隙度與體孔隙度的轉化。

上述式（1）—（5）描述了多孔介質內部結構和孔隙分布情況，是描述多孔介質內部輸運物理現象的重要公式。

1.2 孔隙迂曲特征描述

假設多孔介質是由一束橫截面積不同的迂曲毛細管道組成，在該模型中，單根迂曲毛細管道的長度L(λ) 與管道直徑λ的關系滿足分形冪規律，表示為

式中：L0為毛細管流動方向的特征長度，m。根據分形理論，L0可以通過L0=計算得到。須要注意的是L0不是多孔介質的實際邊長［21］。Dt是迂曲分形維數，Dt越高表示毛細管道越彎曲。在二維平面內，當Dt=1 時，表示毛細管道是直管道，當Dt=2 時，表示毛細管道非常彎曲，已經填充了整個二維平面。根據式（6），迂曲度可以定義為

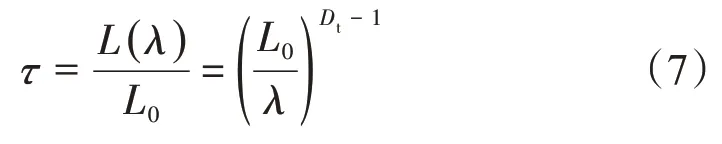
2 多孔介質中氣體擴散的分形模型

氣體在多孔介質中的擴散問題影響因素眾多，其中孔隙結構為主要的影響因素。當孔隙直徑不同時，氣體擴散的規律也不同。Beskok 等［4］通過實驗給出了描述氣體在一維圓管中氣體體積流量的模型，該模型根據Hagen-Poiseuille 方程修正得到，其表達式為

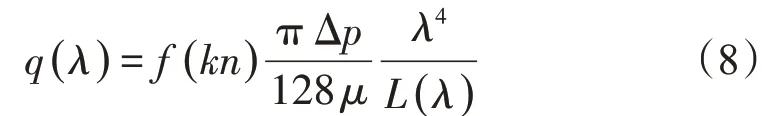
式中：kn為克努森數，kn=l/λ，定義為氣體分子的平均自由程l與孔隙直徑λ的比值，l的單位為m；Δp為毛細管中的氣體壓力差，Pa；μ為氣體黏度，Pa·s。f(kn)為滲透率修正因子，此因子只與kn有關，其表達式為

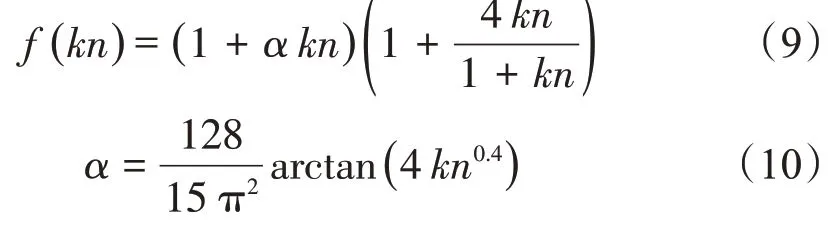
根據kn的不同，氣體在致密多孔介質中可以分為連續介質區、滑移區、過渡區和自由分子區等4 個流動區域，但是，將式（9）和式（10）代入式（8）后得到的公式具有很強的非線性特征，不易求解，應用價值不大［22］。為了得到廣泛適用的滲透率修正因子，使用matlab 多項式曲線擬合工具，對式（9）進行分段擬合。

當kn≤0.001和0.001＜kn≤0.100時，氣體流動處于連續介質區和滑移區。運用泰勒公式將式（10）化簡后再代入式（9），然后忽略滲透率修正因子的二階和高階修正，保留一級修正。此時，f(kn)=1+4kn，據文獻［23］報道，該公式正是Klinkengerg 于1941 年給出的考慮滑脫效應的氣測滲透率的數學表達式，這里的4kn即為滑移因子，但是忽略了二階和高級修正會導致簡化模型值小于Beskok模型值，而通過曲線擬合的方式得到的擬合公式f(kn)=1+4.8 kn其簡化模型值與Beskok 模型值比較吻合。相對誤差為0.060%～0.272%，度量擬合優度的統計量r2可達0.999 4。

當0.1 ＜kn≤10.0 和kn＞10 時，氣體處于過渡區和自由分子區。過渡區的擬合公式為f(kn)=0.8+6.2kn，相對誤差為1.3%～8.5%，統計量r2為0.992。自由分子區的擬合公式為f(kn)=-4.1 +6.65kn，相對誤差為0.11%～1.93%，統計量r2為0.999。

綜上，通過對滲透率修正因子曲線擬合而簡化得到的模型如下

通過對式（8）的擬合得到分段函數與原函數的對比（圖1），可以看出簡化后的模型與原模型擬合誤差較小，精確度較高。通過對滲透率修正因子的簡化，不僅為后續理論計算和求解提供了基礎，同時也有利于Beskok 模型的推廣。

圖1 Beskok 模型與簡化模型的對比Fig.1 Comparison between Beskok model and simplified model

所以一維圓管中氣體體積流量公式也可以用一個分段函數來描述

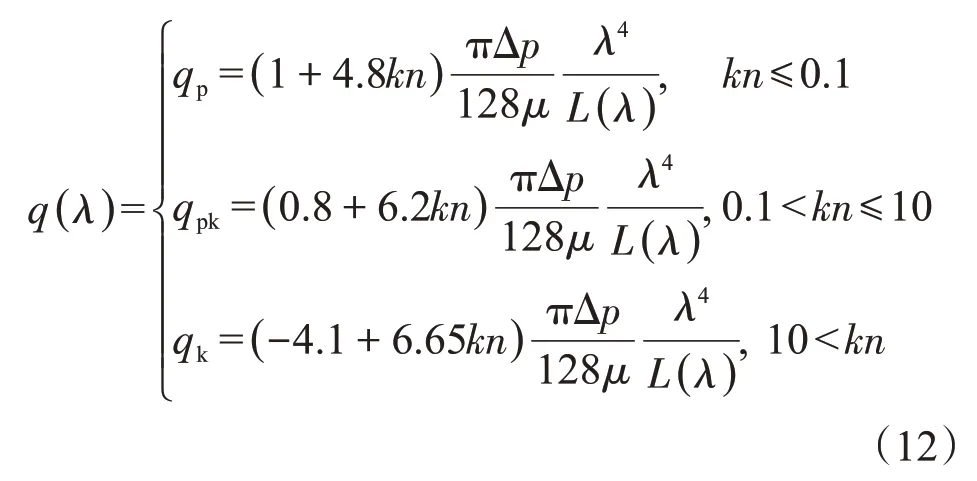
由于多孔介質具有不規則性和復雜性，在同一多孔介質中孔隙大小差別很大，這使得多種流動區域在同一多孔介質中同時存在，根據氣體流動區域的劃分，計算氣體通過橫截面的流量公式如下［17］

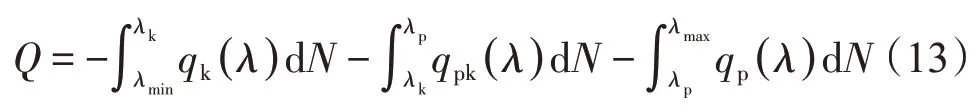
式中：λk=0.1l為滑移區和過渡區的臨界直徑；λp=10l為過渡區和自由分子區的臨界直徑。

聯合式（2）、式（5）、式（11）和式（12）可得

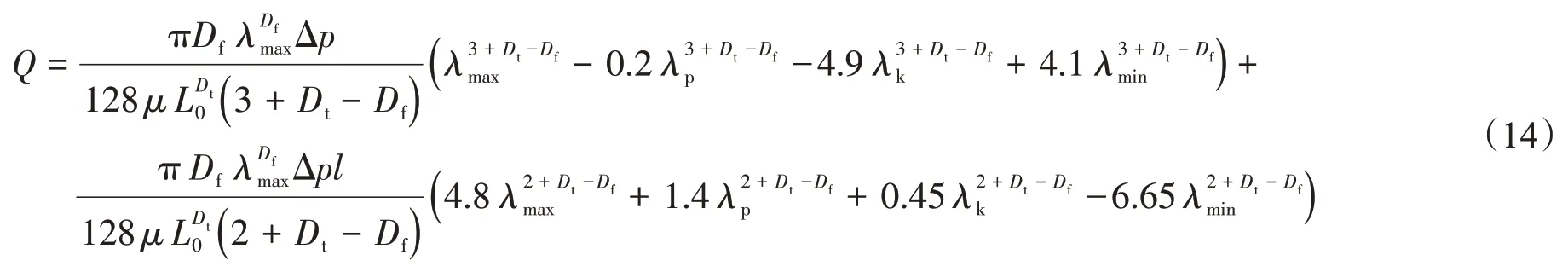
根據菲克定律，氣體在多孔介質中擴散的總的摩爾流率為［15］

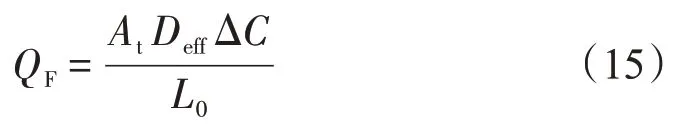
式中：QF為氣體摩爾流率，mol/s；At為多孔介質總的截面積，m2；Deff為有效擴散系數，m2/s；ΔC為多孔介質孔道兩端的濃度差，ΔC=Δp/(RT)，其中，R為氣體常數8.314J/(mol·K) ；T為溫度，K。計算時須要將氣體摩爾流率轉化為氣體體積流量。

聯合式（5）、式（6）、式（13）和式（14），可以求出

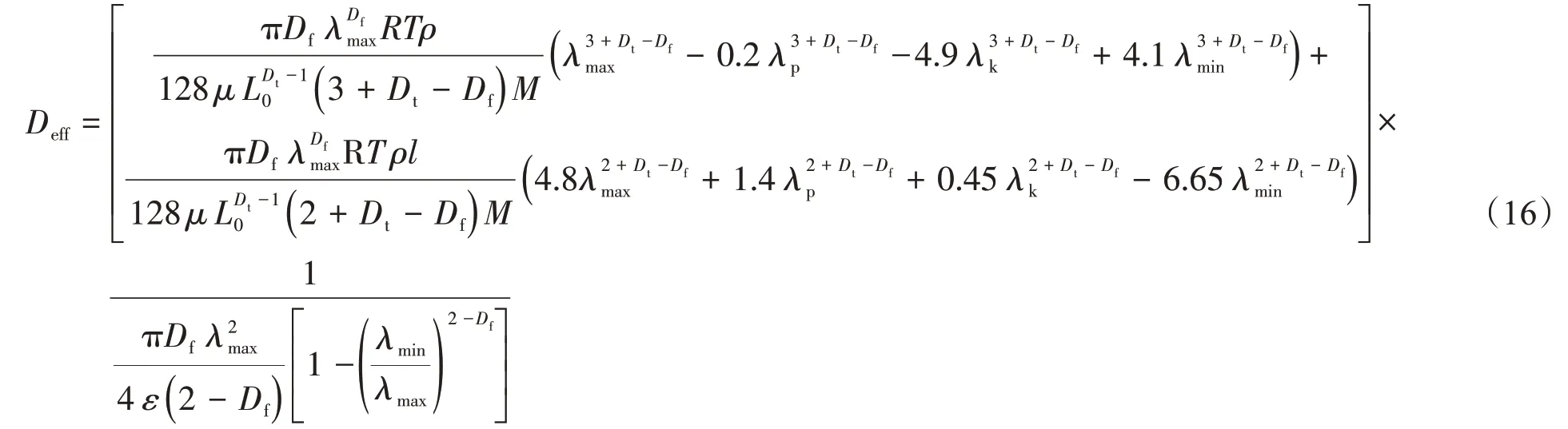
式（16）是基于滲透率修正因子、迂曲毛細管束模型、分形理論和菲克定律求出來的多孔介質氣體擴散模型。此模型的每一個參數都具有物理意義，不包含經驗常數。式（16）表明，氣體有效擴散系數與多孔介質面積分形維數、迂曲分形維數、孔隙度、溫度、最大與最小孔隙直徑、氣體分子平均自由程、氣體摩爾質量、氣體密度和黏度等均有關，并且描述了在不同流動區域共同作用下多孔介質中氣體擴散的詳細機理。

通過式（16）可得知這些參數對氣體有效擴散系數的影響，并應用于工程實踐中的相關參數分析。

3 分析和討論

本文建立的氣體有效擴散系數包含了2 類參數。一類是關于多孔介質孔隙數目和結構的參數，如多孔介質面積分形維數、迂曲分形維數、特征長度、孔隙度等。另一類是關于氣體的性質參數，如密度、摩爾質量、黏度、氣體分子平均自由程等。

多孔介質的結構參數通過分形理論的描述和計算得出，面積分形維數由以下公式來確定

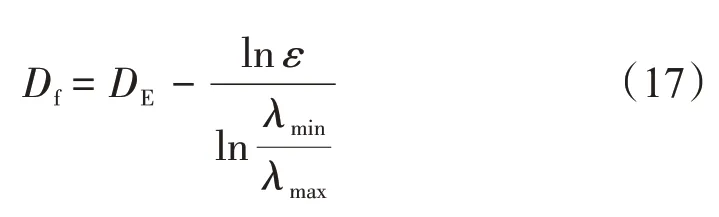
式中：DE為歐幾里德維數，在二維空間中，DE=2；在三維空間中，DE=3。該文是在二維平面上建立的模型，所以DE=2。Feng 等［24］歸納了孔隙度和面積分形維數的實驗數據，結果顯示當λmin/λmax≈10-3時，理論模型值與實驗結果比較吻合。

對于迂曲分形維數，尹帥等［25］分析了常規及非常規儲層巖石的分形特征。運用壓汞法和吸附法研究得到了具有分形特性的多孔介質的迂曲分形維數，其中砂巖多孔介質的迂曲分形維數為1.207～1.704，頁巖多孔介質的迂曲分形維數為1.668～2.187。

然后將已有實驗數據與本文提出的有效擴散系數的理論模型進行對比。Currie［26］將H2作為擴散氣體，使用了多種不同的多孔介質來進行擴散實驗。須要注意的是，實驗中一般使用體孔隙度，而理論模型中是用面孔隙度。須要借助關系式Φ=，把面孔隙度轉化為體孔隙度。其中=1+0.63ln(1/Φ)，該公式由實驗數據擬合得到［1］。

表1 為建立的模型的部分參數：

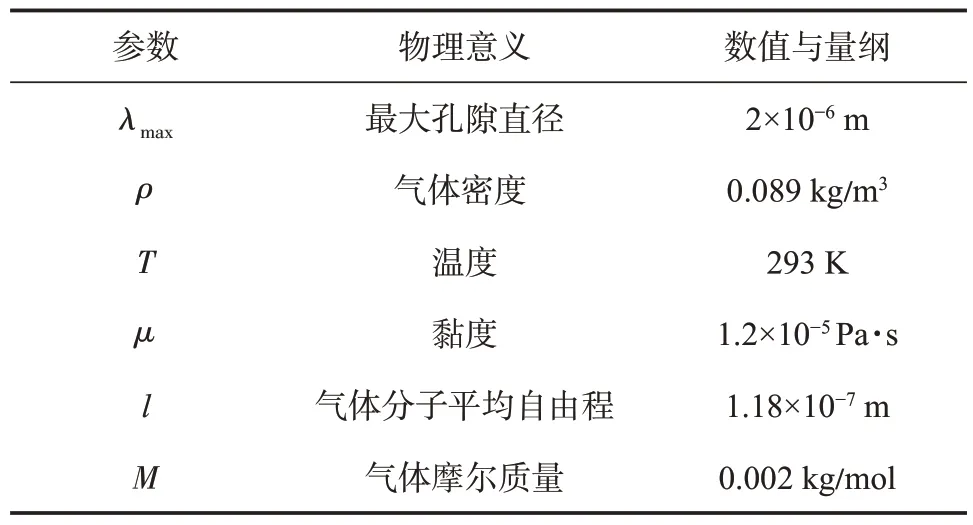
表1 分形模型中的部分參數與數值Table 1 Some parameters and values in the fractal model

將以上數據和公式（17）代入式（16）可以得到圖2 中的函數關系，圖2 顯示氣體有效擴散系數的預測值隨著孔隙度的增加而增加，因為隨著孔隙度的增加，氣體擴散的區域和路徑會增多，有效擴散系數相應增加。當孔隙度超過0.65 時，模型預測值會低于實際值，因為該模型中的最大孔隙直徑使用的是固定值。通過對比模型預測值與實驗數據，可知該模型能夠準確地計算氣體在分形多孔介質中的有效擴散系數。本次建立的理論模型可以用于多孔介質微納米級孔隙情況下的單相氣體擴散計算，可以為非常規天然氣資源開采提供關鍵參數，也可以為氣液兩相或者多相滲透與擴散提供參考。

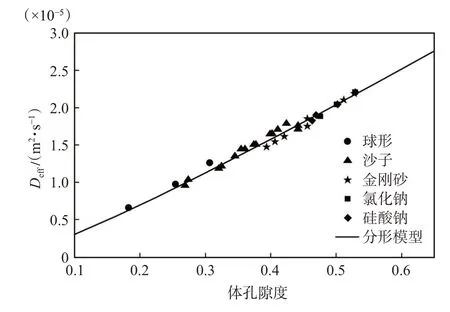
圖2 分形模型的氣體有效擴散系數與文獻［26］實驗數據對比Fig.2 Comparison of effective gas diffusion coefficient of fractal model with experimental data in reference

圖3 為孔道迂曲分形維數分別取1.5，1.6，1.7時，氣體有效擴散系數隨著多孔介質面積分形維數的變化趨勢。從圖3 可以得出，面積分形維數越大，氣體有效擴散系數也越大。因為面積分形維數增加時，孔隙數目也會增加，孔隙度也會增大，導致擴散相對更加容易。當面積分形維數一定時，迂曲分形維數增加，氣體有效擴散系數會減小。因為迂曲分形維數越大，表明孔道毛細管越彎曲，擴散阻力越大，導致擴散性能減小。

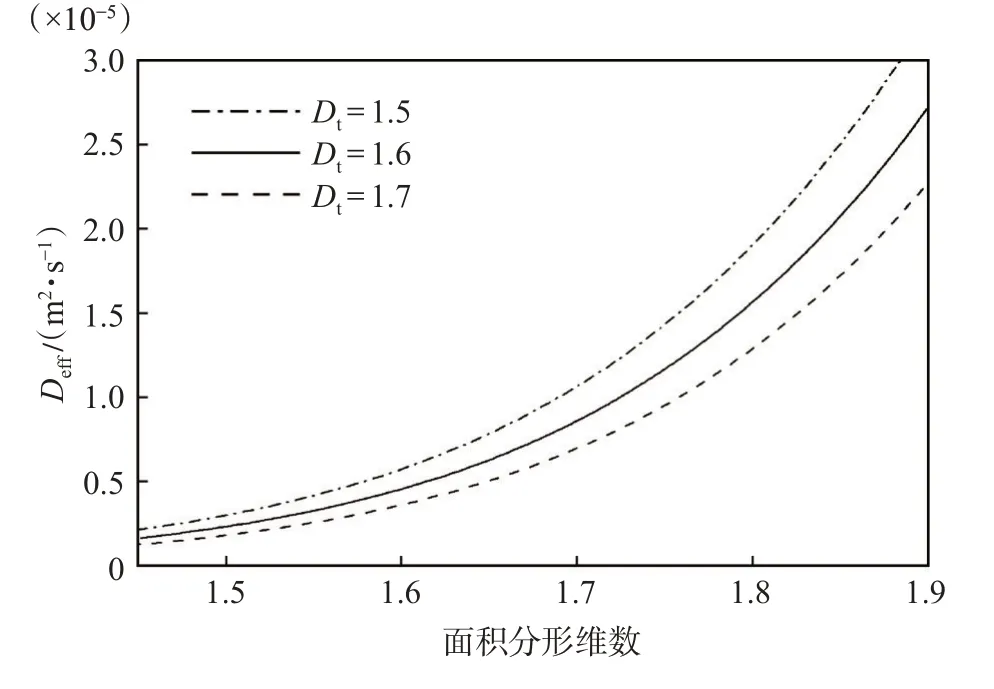
圖3 面積分形維數和迂曲分形維數對氣體有效擴散系數的影響Fig.3 Effect of area fractal dimension and tortuous fractal dimension on effective gas diffusion coefficient

圖4 為考慮滑移因子的模型與不考慮滑移因子模型的對比。據文獻［23］報道，Klinkengerg 于1941 年發現了滑移現象，具體表現為氣體的表觀滲透率明顯大于絕對滲透率。從圖4 可以看出當考慮滑移因子時，氣體的有效擴散系數大于未考慮滑移因子的氣體有效擴散系數，這與Klinkengerg 描述的現象一致。由圖4 分析可知，在孔隙直徑較大的情況下，滑移因子的影響越來越小，當孔隙直徑較小時，滑移因子對有效擴散系數的影響較大，這與滑脫效應一般發生在低滲透率和低孔隙度相一致。從圖4 還可以看出，考慮了滑移因子的分形模型與不同多孔介質的實驗數據更加吻合，這表明考慮了滑移因子的分形模型能夠適用于更多種類的多孔介質。

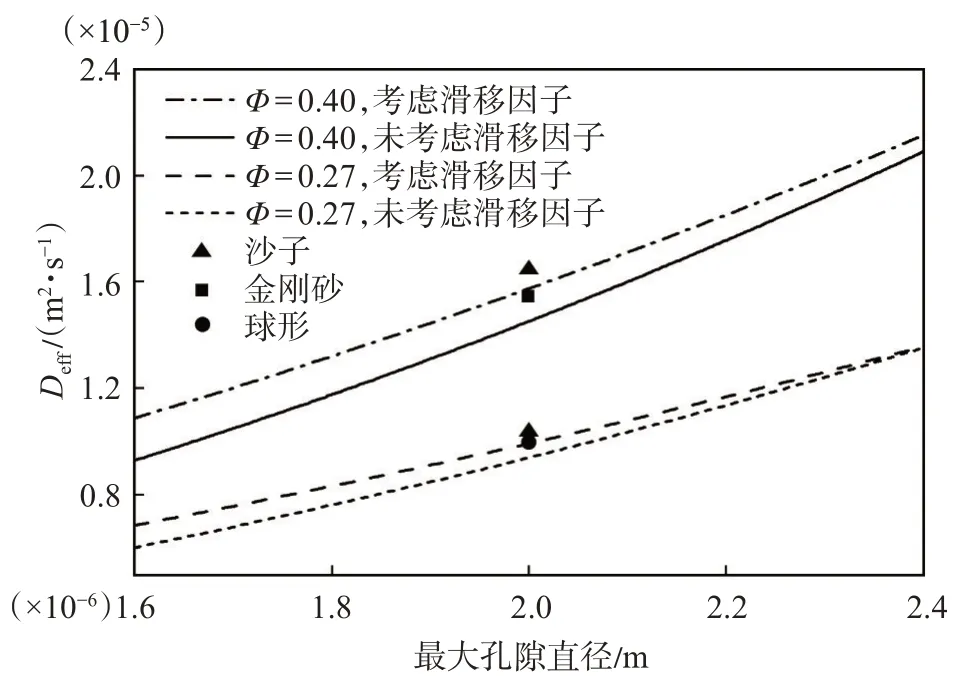
圖4 滑移因子對氣體有效擴散系數的影響Fig.4 Effect of slip factor on effective gas diffusion coefficient

圖5 為在不同最大孔隙直徑下，有效擴散系數隨孔隙度變化的情況。

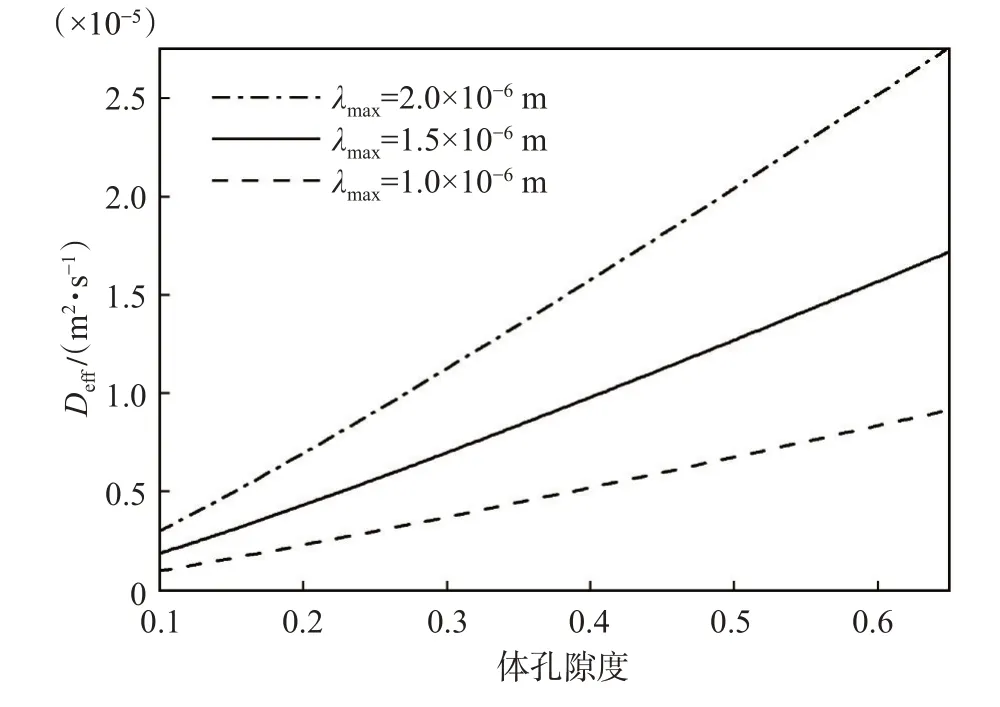
圖5 最大孔隙直徑對氣體有效擴散系數的影響Fig.5 Effect of maximum pore diameter on effective gas diffusion coefficient

從圖5 可以得出，當最大孔隙直徑減小時，氣體有效擴散系數也會減小。因為根據分形理論，分形多孔介質的面積分形維數、迂曲分形維數、最小最大孔徑比、擴散截面面積等都與最大孔隙直徑有關，所以最大孔隙直徑是氣體有效擴散系數的主要影響因素。

圖6 為使用不同的擴散氣體時，有效擴散系數隨孔隙度的變化。由圖6 可知，不同的氣體在多孔介質中的有效擴散系數不同，當擴散的氣體的摩爾質量，或者氣體密度增加時，有效擴散系數會減小。因為氣體質量越大，擴散速率就會越小，有效擴散系數也會越小，這與氣體擴散定律描述的現象一致。

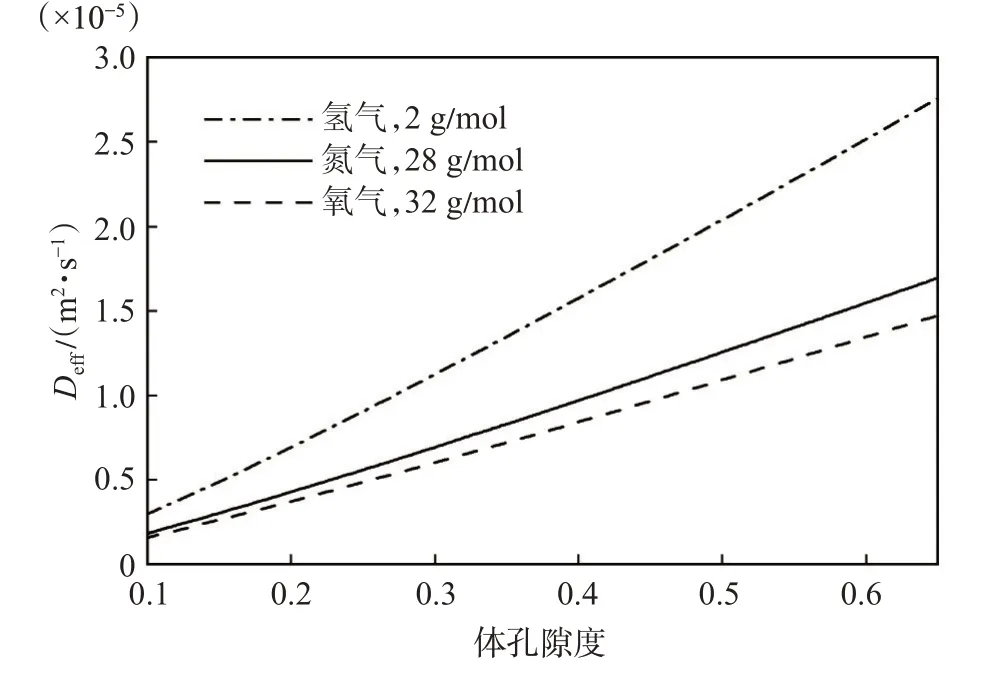
圖6 不同氣體對氣體有效擴散系數的影響Fig.6 Effect of different kinds of gases on effective gas diffusion coefficient

4 結論

（1）基于多孔介質的分形特征、迂曲毛細管束模型、菲克定律、滲透率修正因子建立了多孔介質中氣體擴散的分形模型。該模型包含了多孔介質面積分形維數、迂曲分形維數、孔隙度、最大孔隙直徑、氣體密度和摩爾質量等參數。通過參數分析可以發現：多孔介質孔隙度、面積分形維數、最大孔隙直徑、氣體的物理性質等對有效擴散系數均有顯著影響。

（2）對比分形多孔介質氣體擴散模型與Currie關于氣體擴散率的數據發現：體孔隙度為0.10～0.65 時，模型與多種不同的多孔介質實驗數據均具有較好的一致性，說明該模型可以用于計算具有分形特性的多孔介質的氣體有效擴散系數，對非常規天然氣在實際多孔介質中的有效擴散系數的計算具有一定的參考意義。同時也能為后續研究多孔介質氣液兩相或多相滲透與擴散提供參考。

（3）考慮滑移因子的氣體有效擴散系數大于未考慮滑移因子的氣體有效擴散系數，在較小的孔隙直徑下，兩者的差距比較明顯，隨著孔隙直徑的增大，兩者的差異逐漸減小，直至相等。考慮了滑移因子的氣體有效擴散系數與Currie 關于氣體擴散率的實驗數據更加吻合。