諧波減速器中薄壁軸承接觸載荷-應力計算仿真研究

董紹江，穆書鋒，湯寶平，梁 天

（1.重慶交通大學機電與車輛工程學院，重慶400074；2.重慶大學機械傳動國家重點實驗室，重慶400030）

1 引言

工業機器人配備的諧波減速器主要有鋼輪、柔輪和波發生器三個部件組成，而波發生器中柔性支撐的薄壁軸承作為關鍵零部件，對諧波減速器的運轉平穩性、傳動精度以及復雜工況下工作的整體可靠性等關鍵性能指標具有重要影響。

國內外對薄壁軸承接觸問題進行了許多相關研究。國內：文獻[1]較早提出并推導了一種計算安裝在薄壁支座中的向心軸承在受載后各滾動體負荷的力學模型和計算方法；文獻[2-3]根據諧波傳動中薄壁軸承受載工況，提出薄壁軸承載荷分布計算模型；文獻[4-6]利用ANSYS 軟件面-面接觸方式中柔-柔接觸對推力球軸承赫茲接觸問題進行求解，指出不考慮套圈變形進行薄壁軸承力學特性計算時，誤差較大。國外：文獻[7]對柔性結構的軸承支座系統，提供一種標準有限元法中的剛度矩陣來分析滾動軸承的載荷位移和應力分布；文獻[8-9]考慮軸承柔性外圈和橢圓內圈情況下，對軸承滾動體載荷-變形進行了數值分析。因此，對柔性套圈的薄壁軸承的接觸載荷問題一直以來都是工程研究的熱點問題。

擬以某工業機器人諧波減速器薄壁軸承為例，利用ANSYS軟件建立薄壁軸承柔-柔接觸有限元三維模型，模擬諧波減速器中薄壁軸承受載工況，對其套圈變形后滾動體接觸載荷-應力分布進行仿真分析，并與基于柔性套圈變形假設得到的薄壁軸承接觸載荷-應力數值計算結果進行比較。

2 薄壁軸承接觸載荷-應力計算模型

當軸承的一個或兩個套圈為柔性時，為了確定滾動體接觸載荷分布，必須確定承載套圈圓周各點的變形[10-11]。根據薄壁圓環平面彎曲撓性變形理論[9-10]，得到環件相對圓心φ 處力矩M 作用下彎曲徑向位移u的微分方程：

式中：I—慣性矩；E—彈性模量；R—套圈中性軸半徑。

由于諧波減速器中薄壁軸承內外套圈為薄壁設計，故取軸承一部分作為研究對象。薄壁軸承變形可分為兩部分[2]：第一部分是薄壁軸承外圈在柔輪與鋼輪嚙合力作用下發生的撓性變形ω，內圈與剛性凸輪發生的彈性變形u；第二部分是內外套圈與滾動體表面之間的彈性變形為δir、δor。薄壁軸承柔性套圈變形示意圖，如圖1 所示。

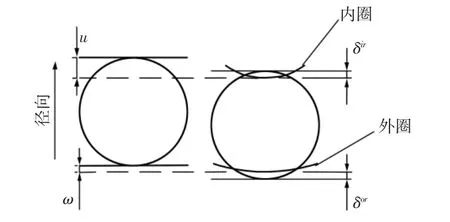
圖1 薄壁軸承柔性套圈變形示意圖Fig.1 Schematic Diagram of Deformation of Thin-Walled Bearing Flexible Ferrule

根據薄壁軸承的柔性套圈在滾動體角度ψi處的變形協調條件，可得方程：

假設軸承有N 個滾動體，由式（2）可建立N 個非線性方程組，利用Newton-Raphson 法求解得到薄壁軸承載荷分布Qi。由于滾子與滾道接觸為非理想接觸用傳統切片法并不能充分估算接觸應力，需先確定軸承載荷分布才能完成接觸應力分析[11]。根據Harris[11-12]得到彈性半空間表面點（x′，y′）的法線接觸壓力和（x，y）點變形之間的關系：

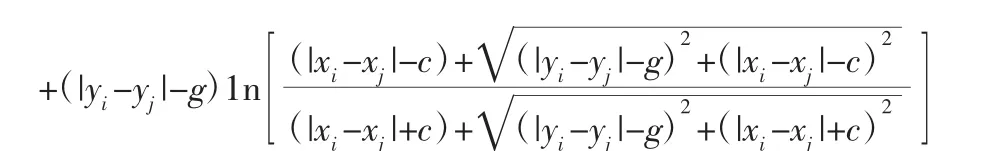
圖2 接觸表面劃分若干小矩形片示意圖Fig.2 Schematic Diagram of the Contact Surface Divided into Several Small Rectangular Pieces

通過改變的值，式（4）和式（5）可以用來精確計算非理想接觸應力，直至在可接受誤差范圍內式（6）得到滿足為止。

3 柔性套圈的薄壁軸承有限元模型

本研究選用某六自由度工業機器人J5 關節配備的國產諧波減速器，其理論計算和仿真分析采用的薄壁軸承結構參數、材料屬性，如表1、表2 所示。實物，如圖3（a）所示。

表1 薄壁軸承各項主要結構參數Tab.1 Main Structural Parameters of Thin-Walled Bearing

表2 薄壁軸承材料屬性Tab.2 Material Properties of Thin-Wall Bearing

3.1 薄壁軸承柔-柔接觸有限元模型

利用ANSYS APDL 的Modeling 建立薄壁軸承有限元模型，考慮到薄壁軸承的倒角、邊棱和保持架等對軸承接觸區域的接觸載荷、應力、變形的影響相對較小，故建模時將其忽略，最終確定整個模型包含內外套圈、23 個滾動體共25 個零件，如圖3（b）所示。ANSYS 軟件可提供包括點-點接觸、點-面接觸、面-面接觸三種方式模擬實際的接觸行為，考慮薄壁軸承柔性套圈屬性，薄壁軸承滾動體與內外套圈滾道接觸采用面-面接觸中的柔-柔接觸。薄壁軸承滾動體相對于套圈較剛，故將滾動體作為柔性目標面，將內圈滾道表面與外圈滾道表面作為柔性接觸面。在各個接觸對中，為確保非線性摩擦接觸收斂以及接觸滲透值較小保證足夠的計算精度，最終確定滾動體與軸承內外套圈接觸摩擦系數設置為0.15，法向接觸剛度因子設置為0.8，接觸算法使用增強拉格朗日法。

3.2 單元選擇與網格劃分

對薄壁軸承內外套圈以及滾動體進行網格劃分時，選擇可以模擬大變形的20 節點SOLID186 六面體單元，將整個薄壁軸承模型拓撲結構分解為規則的幾何體，并運用掃略法和映射法實現對整體模型的網格劃分。并對接觸區域進行局部網格細化，接觸區域的目標面采用TARGE170 單元，而接觸面采用CONTA174 單元，從而保證計算效率和計算精度。經反復調試，最終確定網格數量340458，為保證計算效率運用T7910 移動工作站，至強E5 處理強，32G 內存。

3.3 邊界條件與載荷施加

根據薄壁軸承實際受載工況，對薄壁軸承外圈表面施加壓強為4MPa 的對稱載荷；又因薄壁軸承內圈隨剛性凸輪發生強制變形，故內圈約束方程設置為：ω=0.324cos（2φ），其中，φ＝（0～2）π。對薄壁軸承滾動體在柱坐標下約束切向位移來模擬保持架約束；對薄壁軸承內、外套圈側面施加軸向約束模擬薄壁軸承在實際過程中，不能發生軸向運動。

4 薄壁軸承接觸載荷-應力計算與仿真

根據提取的ANSYS 薄壁軸承內外套圈仿真變形曲線，如圖4 所示。可知，裝配受載的薄壁軸承發生較大撓曲變形且最大變形發生在凸輪長軸左右，薄壁軸承滾動體也發生較大剛性位移，滾動體-滾道接觸已經并非為理想接觸，這有別于剛性套圈得到的軸承變形規律。

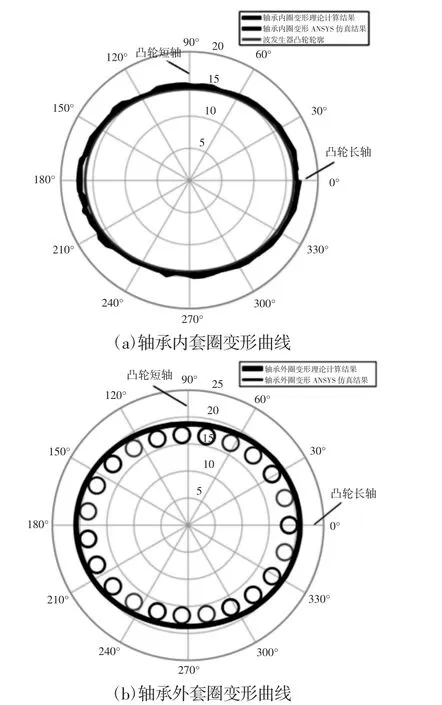
圖4 薄壁軸承內外套圈變形曲線Fig.4 Deformation Curve of Inner and Outer Rings of Thin-Walled Bearing

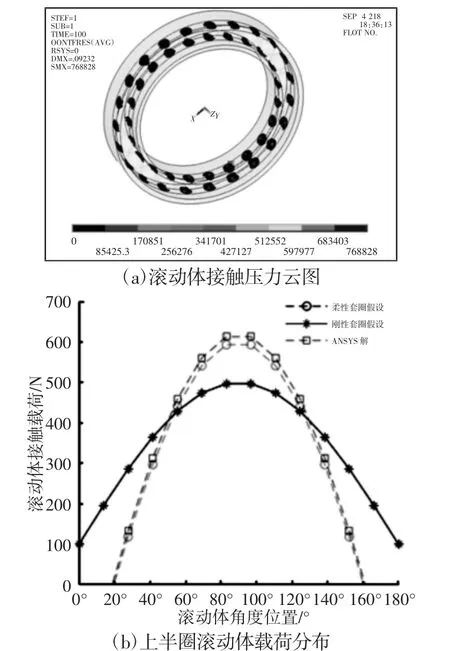
圖5 薄壁軸承接觸壓力與載荷分布Fig.5 Thin-Walled Bearing Contact Pressure and Load Distribution

文獻[11-12]通過切片法給出剛性套圈假設下理想滾動體-滾道接觸區域每個切片的載荷分布為：

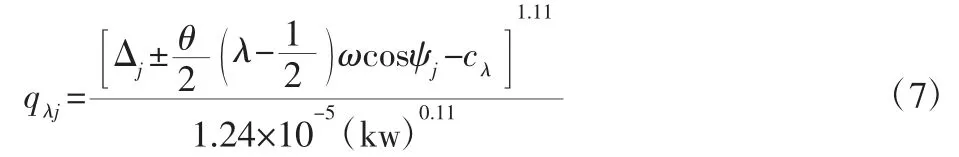
總的滾動體載荷為：

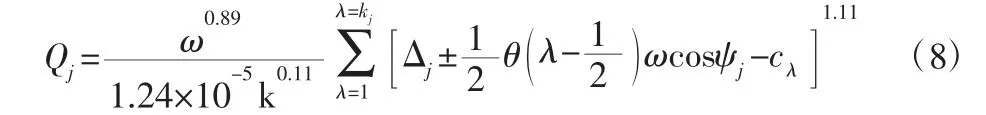
ANSYS 仿真可得到的薄壁軸承滾動體接觸壓力云圖，如圖5（a）所示。通過APDL 命令流提取接觸面、目標面節點接觸壓力進行積分即可求得滾動體接觸載荷。如圖5（b）所示可知，基于柔性套圈假設得到的薄壁軸承滾動體接觸載荷與ANSYS 仿真結果更加接近，此時用剛性套圈假設分析諧波減速器中柔性套圈的薄壁軸承的載荷分布已不再適用，如式（8）所示。

同理，可得到薄壁軸承滾動體接觸區域應力分布云圖和三維曲面分布圖，如圖6（a）～圖6（c）所示。仔細觀察接觸區域輪廓近似橢圓，符合Hertz 接觸理論規律。從圖6（d）可知，用滾動體-滾道非理想接觸得到的應力計算結果相對于傳統理想接觸切片法（式（7））估算軸承接觸應力更加精確、合理，誤差相對較小。具體理論計算數值解和仿真結果，如表3 所示。可發現仿真結果和理論計算結果誤差相對較小，從而驗證用ANSYS 模擬薄壁軸承柔性接觸問題的合理性、有效性。

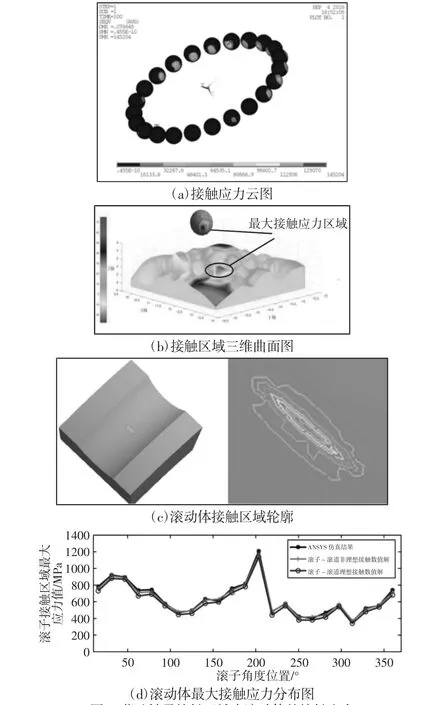
圖6 薄壁軸承接觸區域內滾動體的接觸應力Fig.6 Contact Stress of Rolling Elements in Contact Area of Thin-Walled Bearing

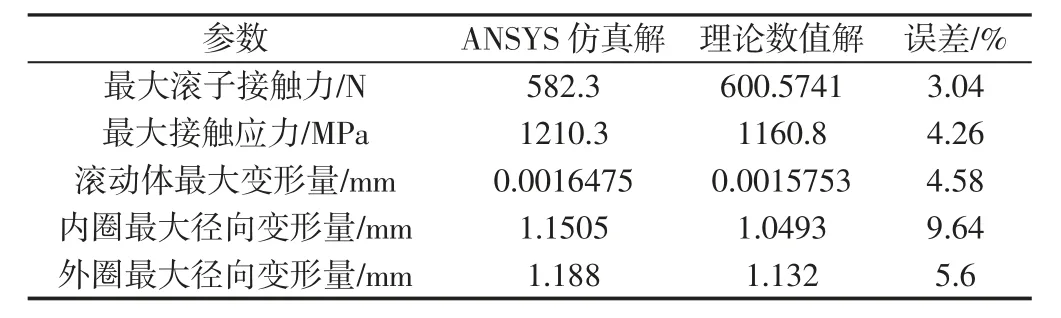
表3 理論數值解與仿真結果對比Tab.3 Comparison of Theoretical Numerical and Simulation

5 結論

基于柔性套圈假設得到諧波減速器中薄壁軸承接觸載荷-應力計算模型，并建立薄壁軸承柔-柔接觸有限元仿真模型，通過理論計算與仿真分析結果對比發現，兩者誤差相對較小，為薄壁軸承設計以及壽命評估提供參考。結論如下：（1）裝配受載后諧波減速器中的薄壁軸承內外套圈發生變形，最大變形發生在凸輪長軸附近。（2）薄壁軸承套圈的變形使滾動體發生剛性移動，滾動體與內外套圈的接觸為非理想的柔性接觸，用ANSYS 和柔性套圈假設模擬計算薄壁軸承的柔-柔接觸載荷-應力有一定的合理性。（3）采用傳統剛性套圈假設以及切片法分析薄壁軸承接觸載荷-應力誤差相對較大，有一定的局限性。