數(shù)學(xué)教學(xué)贏在變通
浙江省臨海市回浦高中 金文學(xué)

(2)略。
評(píng)析:含參不等式分離參數(shù)后的形式因題、因分法而異,因此,解決含參不等式恒成立問(wèn)題需把握住下述結(jié)論:(1)f(x)≥g(a)恒成立f(x)min≥g(a);(2)f(x)≤g(a)恒成立f(x)max≤g(a)。
一看此路不通,便不為此大費(fèi)周折,而是獨(dú)辟蹊徑,因?yàn)橥ㄍ晒Φ穆凡恢挂粭l,變則通,通則久,山間的溪流也懂得:只有變通方向,才能避免被巖石撞擊,會(huì)適時(shí)轉(zhuǎn)彎前行。當(dāng)執(zhí)著“行到水窮處”時(shí),就需要“坐看云起時(shí)”的變通;當(dāng)執(zhí)著“山窮水復(fù)疑無(wú)路”時(shí),就需要“柳暗花明又一村”的變通。
【例2】已知函數(shù)f(x)=x2+bx+c(b,c∈R),對(duì)任意的x∈R,恒有f'(x)≤f(x)。
(1)證明:當(dāng)x≥0時(shí),f(x)≤(x+c)2。
(2)若對(duì)滿足題設(shè)條件的任意b,c,不等式f(c)-f(b)≤M(c2-b2)恒成立,求M的最小值。
解析:(1)略。
(2)由f''(x)≤f(x),即x2+(b-2)x+c-b≥0恒成立,
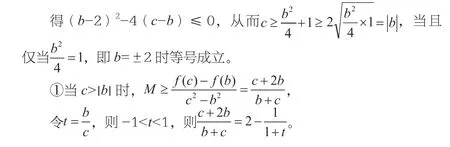

遇到問(wèn)題時(shí),不要頑固執(zhí)著地對(duì)待,而應(yīng)靈活應(yīng)付變化,順勢(shì)而為,善于變通。當(dāng)你彷徨或者是困難的時(shí)候,不要輕易放棄,必須學(xué)會(huì)變通,改變自己的思考空間,要沖出習(xí)慣性思維的樊籠。
【例3】設(shè)函數(shù)f(x)=ex-1-x-ax2。
(1)若a=0,求f(x)的單調(diào)區(qū)間。
(2)若x≥0時(shí),f(x)≥0,求a的取值范圍。
解析:(1)略。
(2)由f(x)≥0對(duì)所有的x≥0成立,可得:
①當(dāng)x=0時(shí),a∈R;


數(shù)學(xué)思維的靈活性表現(xiàn)在整體把握問(wèn)題的基礎(chǔ)上靈活解決問(wèn)題的能力。每年穩(wěn)中有變的考綱和試卷變化,尤其需要教師教學(xué)方法的融會(huì)貫通,引導(dǎo)學(xué)生對(duì)問(wèn)題進(jìn)行深層次的剖析,教會(huì)學(xué)生變通的數(shù)學(xué)思維,重視數(shù)學(xué)的核心視角,重3視數(shù)學(xué)的通性通法,提高學(xué)生思考的深刻性和靈活性。
- 數(shù)學(xué)大世界的其它文章
- 讓課堂“微”起來(lái)
——《“微課”在小學(xué)數(shù)學(xué)圖形與幾何教學(xué)中有效應(yīng)用的研究》階段性總結(jié) - 以問(wèn)導(dǎo)學(xué)
——小學(xué)數(shù)學(xué)課堂中問(wèn)題創(chuàng)設(shè)的實(shí)踐探究 - 呈現(xiàn)你不知道的精彩
——人教版教材“你知道嗎”使用策略例談 - 經(jīng)歷過(guò)程,積累數(shù)學(xué)活動(dòng)經(jīng)驗(yàn)
- 借力信息技術(shù),促進(jìn)學(xué)生空間想象力發(fā)展
- 讓學(xué)生感受生活中的“數(shù)學(xué)美”

