無錯區分兩個任意分布的未知緯線態

呂彥霖， 祝鳳榮

(西南交通大學物理科學與技術學院， 成都 611756)

1 引 言

量子通信和量子計算中的許多應用都需要用到量子態分辨，例如：量子秘密共享[1]、量子密鑰分發[2]、量子安全直接通信[3]、量子隱形傳態[4-6]等. 量子態分辨問題是指許多量子態構成了一個集合，從這個集合中取出一個量子態，如何確定取出的這個量子態是集合中的哪個態. 這不是一個容易解決的問題，因為任意一個未知量子態不可能被精確復制(雖然無法精確復制，但是人們可以實現非精確的量子克隆). 當集合中的量子態互相不正交時，我們無法百分百確定取出的這個態是集合中的哪個態. 在量子態分辨問題中，人們常用的方案主要有兩種，分別是最小容錯區分(測量結果可能會出錯，但是需確保出錯概率取到最低)和最優無錯區分(測量結果不會出錯，但可能會出現測量結果不能確定待確定態是哪個態的結果，并且需確保出現這種結果的概率取到最低).

為了對兩個未知態進行無錯分辨，2005年Bergou和Hillery[7]設計了一種可編程的量子分辨器. 該設備可以在不知道這兩個態信息的條件下，分辨出數據寄存器中的待確定態.這樣的可編程設備由兩個程序寄存器A、C和一個數據寄存器B構成，假設程序寄存器A和C中分別儲存著量子比特態|ψ1>和|ψ2>，數據寄存器B中儲存著待確定態|ψ?>(|ψ?>是|ψ1>和|ψ2>中的一個，先驗概率分別為η1和η2，且η1+η2=1), 則可編程量子分辨器的主要作用是分辨下面兩個總輸入態：

|Ψ1>=|ψ1>A|ψ1>B|ψ2>C

|Ψ2>=|ψ1>A|ψ2>B|ψ2>C

(1)

這個分辨器能夠以某種成功概率告訴我們待確定態|ψ?>與|ψ1>和|ψ2>中的哪一個相同，所以對兩個未知態的最優無錯區分問題其實就是針對這兩個態尋找最優的無歧分辨器. 可編程的量子分辨器就是一個可編程的量子測量器，在數學上有一個全局廣義測量與其對應，因此我們可以通過一組廣義測量算符來表示它.量子態分辨問題其實就是針對不同類型的態尋找最優的測量算符, 并且計算出與其對應的最大成功概率.

上面介紹的這個分辨器中的輸入態|ψ1>和|ψ2>都是量子比特態，也就是二維單拷貝的. 在這個分辨器提出之后，人們又對其進行了實驗實現和進一步的推廣，將輸入態|ψ1>和|ψ2>推廣到了都是高維單拷貝的情況[8]和高維任意多拷貝的情況[9-10]. 此外，人們還研究了如何無錯區分N個未知純量子比特態的問題[11]、有關無錯區分三個線性無關對稱態的問題[12].

本文要區分的兩個態是緯線態，它是一種特殊類型的量子比特態，它不像一般量子比特態那樣分布在整個態空間，而是被限制在了布洛赫球體的某一緯度線上. 它可以表示為

(2)

其中，θ是取值范圍[0,π]中的一個常數，φ是取值范圍[0,2π)中的未知數. 它在這個范圍內任意一點出現的概率服從任意的概率密度函數σ(φ)，所以我們要區分的兩個未知緯線態是:

(3)

其中，φ1和φ2是取值范圍[0,2π)中的未知數，它們服從相同的任意概率密度函數σ(φ).

2 測量算符與成功概率的推導

我們實際要無錯區分的兩個總輸入態為：

|Ψ1>=|ψ1>A|ψ1>B|ψ2>C

|Ψ2>=|ψ1>A|ψ2>B|ψ2>C

(4)

這里的|Ψ1>和|Ψ2>都是8維空間中的態，解決這個問題所用到的廣義測量(POVM)應當也是在8維空間中進行的. 為了便于在實驗上實現這個廣義測量，我們可以利用Neumark定理和可編程量子態分辨器的光學實現方法[13]，在一個更大的希爾伯特空間上作正交測量. 首先，我們介紹一個擴大的希爾伯特空間，這個空間是10維的，設:

|000>→|e1>,|010>→|e2>,|001>→|e3>,

|100>→|e4>,|101>→|e6>,|110>→|e7>,

|011>→|e8>,|111>→|e10>

(5)

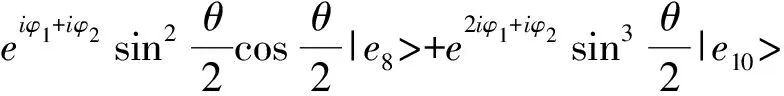
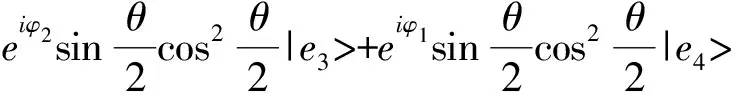
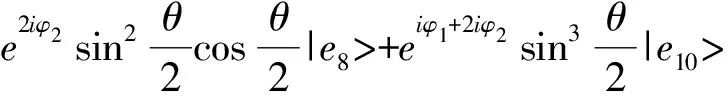
(6)

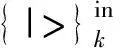
(7)

其中,

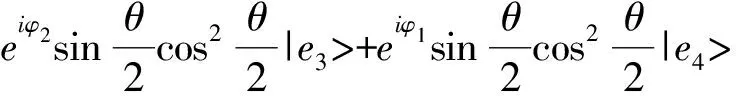
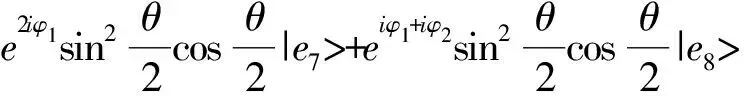
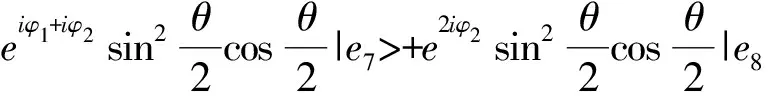
(8)

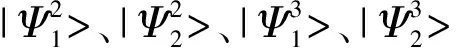
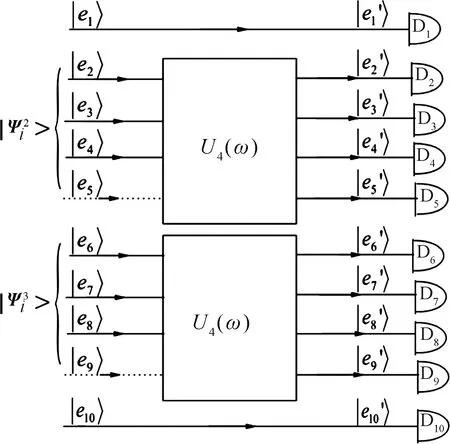
圖1 區分和的分辨器的光學實現

(9)

其中U4(ω)表示為(其推導見第三部分):

(10)

通過U10(ω)，我們可以得到|Ψi>的輸出表示：

(11)

(12)

由此，我們可以在輸出端定義測量算符：

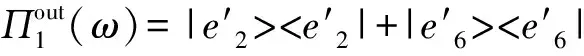
(13)

(14)

令cos2ω=x，則x的取值范圍為[0,1]，此時P(ω)可以表示為

(15)

(16)

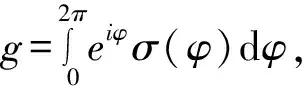
(17)

通過U10(ω)我們可以在輸入端表示出式(13)定義的測量算符

(18)

(19)

經過計算可知：

(20)

則式(17)表示的成功概率對應的測量算符在|ijk>(i,j,k=0,1)張成的8維子空間中可以表示為:

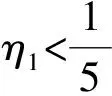
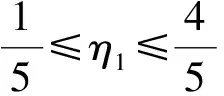
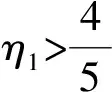
(21)

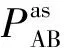
文獻[14]中討論的問題是如何最優無錯區分兩個均勻分布的未知緯線態，得到的最優測量算符為

(22)

這與本文得到的測量算符一致.

3 U4(ω)的推導

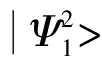
(23)

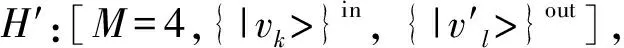
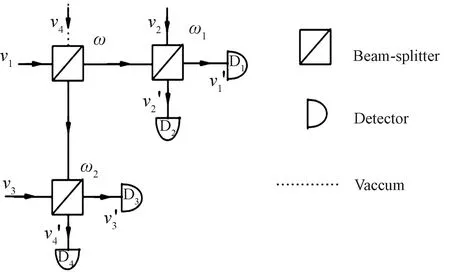
圖2 區分和的分辨器的光學實現Fig.2 Optical realization of the discriminator between

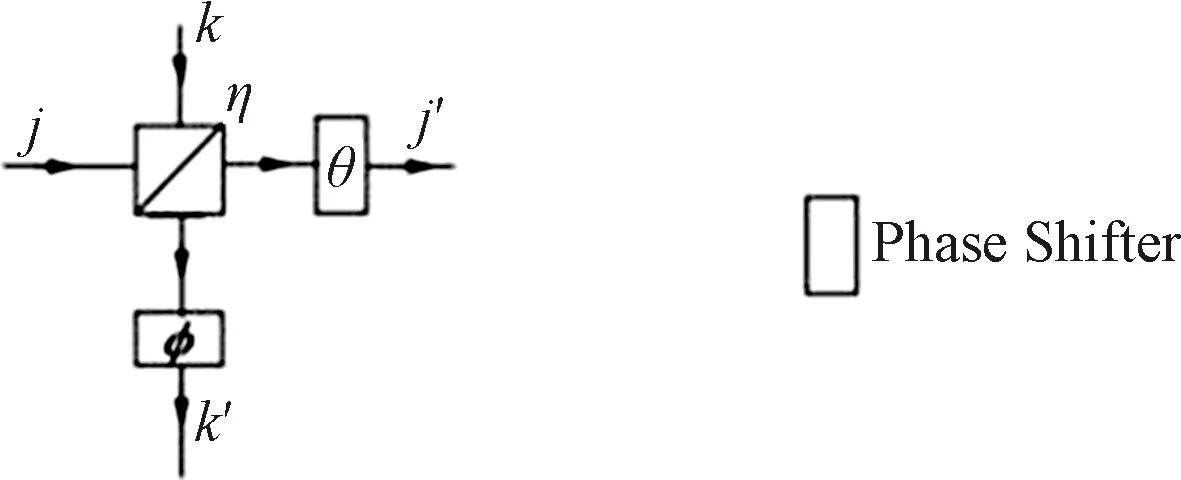
圖3 U2的光學實現Fig.3 Optical realization of U2

(24)

在干涉儀中，分束儀起的作用可以通過一個二維實變換來表示：

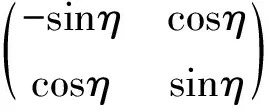
(25)

下面我們來求U4的具體表示.

(26)

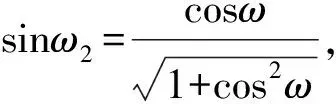
(27)

則，式(26)可以表示為：

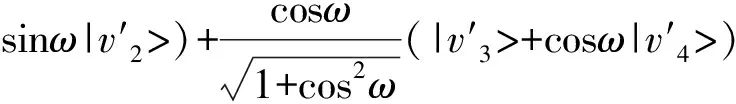
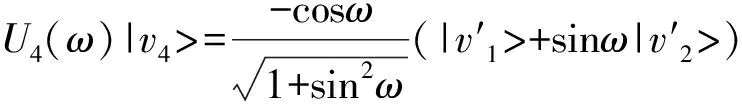
(28)

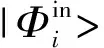
(29)

(30)

4 結 論

我們研究了針對兩個任意分布的未知緯線態的可編程無錯分辨器，得到了測量算符的具體表達式和對應的成功概率，這對于構造可編程分辨器來說具有重要參考意義. 本文得到的測量算符可以無錯區分兩個任意分布的未知緯線態，但是不能確定是否是最優的. 文獻[14]中嚴格推導了當σ(φ)取均勻分布對應的1/2π時的最優測量算符的表達式，這個表達式與本文得到的測量算符相同，這說明，本文得到的測量算符對于無錯區分兩個均勻分布的未知緯線態來說是最優的.