關(guān)于Toeplitz算子與復(fù)合算子在Fock-Sobolev空間上的乘積

秦 杰, 王曉峰

(廣州大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院, 廣州 510006)

(2010 MSC 47B35; 475B32)

1 引 言

在本文中,C表示復(fù)平面,dA表示面積測度. Fock空間F2的定義為

其中H(C)為C上的整函數(shù). 對任意的非負(fù)整數(shù)m, 定義Fock-Sobolev空間F2,m為

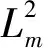
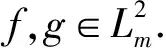
(Pf)(z)=

其中

是F2,m的再生核函數(shù).F2,m的一組標(biāo)準(zhǔn)正交基為

若f是C上的可測函數(shù)且滿足

則稠定義F2,m上以f為符號的Toeplitz算子Tf為

(Tfg)(z)=P(fg)(z),g∈F2,m.

對任意整函數(shù)φ和h, 復(fù)合算子Cφ定義為

Cφh(z)=h°φ.

我們定義F2,m上的Toeplitz算子與復(fù)合算子的乘積為

TfCφh=P(f·h°φ)，CφTfh=P(fh)°φ.

若f是整函數(shù),則TfCφ為加權(quán)復(fù)合算子. 許多數(shù)學(xué)家研究了Fock空間上的復(fù)合算子與加權(quán)復(fù)合算子，如Carswell等[2]第一次完全刻畫了Fock空間上復(fù)合算子的緊性與有界性. Cho 等[3]將其結(jié)論推廣了Fock-Sobolev空間上,并刻畫復(fù)合算子的有限線性組合的緊性與有界性. Le[4]和Ueki[5]研究了Fock空間上加權(quán)復(fù)合算子的有界性和緊性. Tien和Khoi[6]刻畫了作用在兩個不同的Fock空間上的復(fù)合算子的有界性.關(guān)于加權(quán)Fock空間上的正Toepliz、復(fù)合算子及Volterra 積分算子,可參見文獻(xiàn)[7-9].

關(guān)于兩個Toeplitz算子在Fock空間上可交換的問題，Bauer和Lee[10]刻畫了以徑向函數(shù)為符號的Toeplitz算子在Fock空間上的交換性. 隨后, Bauer等[11]討論了以多重調(diào)和函數(shù)為符號的Toeplitz算子在Fock空間上的交換性.此外，Appuhamy等[12]刻畫了以可分離的徑向多項式為符號的Toeplitz算子的換位子.

另外，算子乘積的有界性問題也已經(jīng)被很多數(shù)學(xué)家討論過，如Mengestie[13]刻畫了Volterra型積分算子與復(fù)合算子乘積的有界性和緊性，文獻(xiàn)[14]研究了Toeplitz算子的乘積在Bergman空間上的有界性. 然而，Toeplitz乘積在Bergman空間上的有界性問題直至現(xiàn)在仍未解決. 特別地，關(guān)于Fock空間上Toeplitz算子和復(fù)合算子乘積的有界性及Toeplitz算子與復(fù)合算子可交換的刻畫, 至今仍是空白.

定義

受上述研究的啟發(fā), 我們首先討論了以D中元素為符號的Toeplitz算子和復(fù)合算子乘積CφTf與TfCφ在F2,m上的有界性，進(jìn)而給出了以D′中元素為符號的乘積與在F2,m上有界的充分必要條件. 然后我們刻畫了以D中元素為符號的Toeplitz算子和復(fù)合算子可交換的充分必要條件.

2 Toeplitz算子與復(fù)合算子的乘積

在本節(jié)中, 我們討論Toeplitz算子與復(fù)合算子的乘積的有界性.

引理2.1若i和j是兩個非負(fù)整數(shù), 則

證明 直接計算可知

證畢.

其中{aij}是一個常值序列. 令

f有擬齊次展式

其中

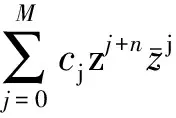
引理2.2設(shè)n,k,N是有限非負(fù)整數(shù). 令

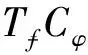
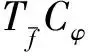
若TfCφ有界,則由引理2.1, 對任意非負(fù)整數(shù)l有

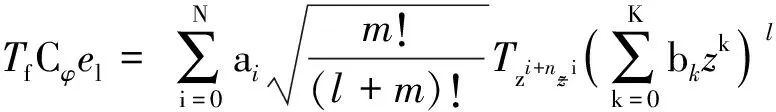
這里

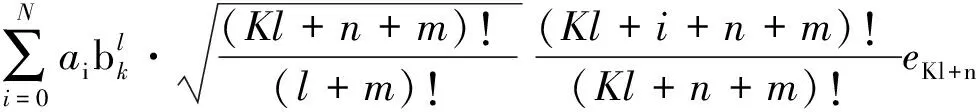
則

記

利用Stirling公式有

這里～表示當(dāng)l→∞時兩項之商有有限正極限. 由aN≠0,bK≠0，我們有

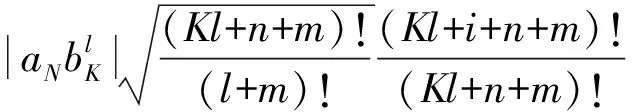
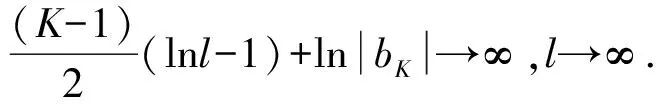
進(jìn)而|b1|≤1. 如果k=|b1|=1. 則N=n=0.

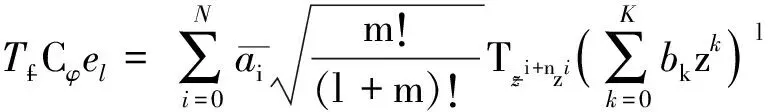
其中

E=TfCφel-

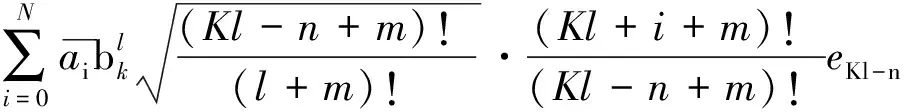
因此,

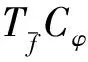
命題2.3設(shè)(f,φ)∈D且f為一個不恒為0的函數(shù). 若TfCφ有界, 則φ(z)=b1z, 其中|b1|≤1.

證明 因為(f,φ)∈D且f是一個不恒為0的函數(shù),我們有

其中bK,fn0,fn1均不為0. 對任意非負(fù)正整數(shù)l, 由引理2.1得

其中

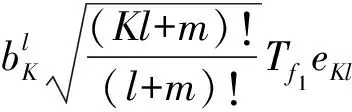
不失一般性, 令

簡單計算可得

由引理2.2，若k=1,則|b1|≤1;若k=|b1|=1,則N=n=0.

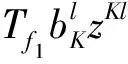
同理，由引理2.2，若k=1,則|b1|≤1;若k=|b1|=1,則n1=0且f0為常值函數(shù). 證畢.

定理2.4設(shè)(f,φ)∈D′,則TfCφ在F2,m上有界當(dāng)且僅當(dāng)下列條件之一成立:

(i)f≡0;

(ii)f為非零常數(shù)函數(shù)且φ(z)=b1z,其中|b1|=1.

證明 充分性顯然,下證必要性. 若f≡0，則TfCφ≡0.在此情形下,TfCφ顯然有界. 故假設(shè)f是一個不恒為0的常數(shù). 由命題2.3可得:φ(z)=b1z,|b1|≤1.由于(f,φ)∈D′,則|b1|=1.令

其中fn0fn1均不為0. 利用命題2.3第一部分的證明得當(dāng)n0=n1時f(z)=f(0).

若n0≠n1,由命題2.3第一部分的證明可知n1=0且f0為常值函數(shù). 則

由引理2.1有

TfnCb1zzl∈Span{el+n},n0≤n<0.

則TfnCb1zel與TfnCb1zel-Tf0Cb1zel正交.因此, 我們有

由引理2.2知fn0為常值函數(shù). 即f為常值函數(shù).證畢.

接下來我們討論CφTf的有界性. 我們有以下引理.

引理2.5設(shè)K是正整數(shù),n與N是有限非負(fù)整數(shù).令

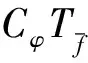
證明 充分性顯然, 下證必要性. 假設(shè)CφTf有界.對任意的非負(fù)正整數(shù)l，我們有

易知Q與(CφTfel-Q)正交.由Stirling公式,

故

‖CφTfel‖2,m≥‖CφTfel-Q‖2,m～

因為‖CφTfel‖2,m有限, 所以k=|b1|=1且N=n=0.由于aN≠0,則f是非零常值函數(shù)且φ(z)=b1z,其中|b1|=1.

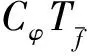
定理2.6設(shè)CφTf在F2,m上有界當(dāng)且僅當(dāng)下列條件之一成立:

(i)f≡0;

(ii)f為非零常數(shù)函數(shù)且φ(z)=b1z,其中|b1|=1.

證明 證明與定理2.4的證明類似, 略.

3 復(fù)合算子與Toeplitz算子的交換性

在本節(jié)中,我們將討論以D中元素為符號的復(fù)合算子與Toeplitz算子的交換性.

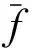
證明 由CφTf=TfCφ易知CφTf1=TfCφ1=Tf1.則

(I-Cφ)Tf1=0

(1)

不失一般性,

其中N和K都是非負(fù)整數(shù). 由(1)式得

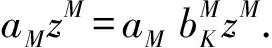
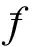
證明本節(jié)的主要結(jié)論需要以下引理.

引理3.2設(shè)K是一個正整數(shù). 令

其中N>K≥1.則CφTf=TfCφ當(dāng)且僅當(dāng)下列條件之一成立:

(i)f為常值函數(shù);

(ii)φ(z)=z.

證明 充分性顯然, 下證必要性. 假設(shè)CφTf=TfCφ.則對任意的非負(fù)整數(shù)l有

CφTfzl=TfCφzl.

故

(2)

當(dāng)l=1時,

化簡可得

a1(m+1)(1-b1)=

(3)

對照系數(shù)可知

a1bKzK-1=0,

?

(4)

故a1bK=0. 考慮以下3種情況.

情形1a1≠0. 由(3)和(4)式可得

b2=b3=…=bK=0,b1=1.

即φ(z)=z.

情形2a1=0，bK≠0. 由(3)和(4)式可得

a1=a2=a3=…=aK=0.

因此

令l=N并代入(2)式有

考慮兩邊的最高次數(shù)得

由上述等式可知K=1或aK+1=0. 如果K≠1,我們考慮zK(N+K-2)與zKN-K-1的系數(shù). 同理可得aK+2=0.類似可得當(dāng)K≠1時,

a1=a2=…=aN=0.

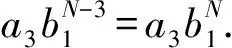
情形3a1=bK=0.(4)式可化簡為

故a2bK-1zK-3=0.由情形a1bK=0的證明可知f為常值函數(shù)或φ(z)=z.證畢.

引理3.3設(shè)K是一個正整數(shù). 令

其中N≤K.則CφTf=TfCφ當(dāng)且僅當(dāng)下列條件之一成立:

(i)f為常值函數(shù)；

(ii)φ(z)=z.

證明 假設(shè)CφTf=TfCφ.則當(dāng)l=1時有

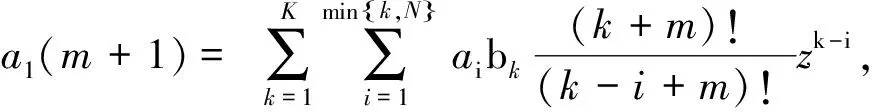
l=1.

若N=0,則結(jié)論成立. 下設(shè)1≤N≤K. 對照系數(shù)可知

a1bKzK-1=0,

?

由引理3.2的證明可知f為常值函數(shù)或φ(z)=z.

引理3.4設(shè)(f,φ)∈D.則CφTf=TfCφ當(dāng)且僅當(dāng)下列條件之一成立:

(i)f為常值函數(shù);

(ii)φ(z)=z.

證明 充分性顯然. 利用引理3.1, 3.2及3.3, 必要性得證.