如何將模型思想融入初中數學教學

施金花

摘 要： 將模型思想融入初中數學教學中，有助于深化學生對數學知識本質的理解，掌握運用數學知識解決問題的思路與方法，促進其學習能力的進一步提升.教學實踐中應結合學生的認知規律以及具體教學內容，采取針對性的融入策略，使學生牢固的掌握相關的數學模型，并靈活應用于解題中.

關鍵詞： 初中數學;模型思想;融入;教學

中圖分類號： G632?????? 文獻標識碼： A?????? 文章編號： 1008-0333（2021）35-0004-02

模型思想是一種運用數學模型解決問題的思想.在該思想指引下可進一步提升學生的學習效率，迅速的找到解決問題的思路.初中數學教學中應為學生剖析相關的理論知識，做好數學模型的歸納，尤其展示模型思想在解題中的具體應用，進一步提高學生的靈活應用能力.

一、剖析模型理論

初中數學涉及有很多的模型，如一次函數模型、二次函數模型、反比例函數模型等.教學中應通過列舉具體的實例為學生講解數學模型的本質，運用數學模型解決問題的思路與方法以及應用注意事項，如構建函數模型時應確定正確的自變量范圍.同時為增強學生運用模型思想解題的自信心，應注重為學生創設熟悉的問題情境，進一步夯實學生所學的理論知識.

例如，在講解二次函數模型時，為學生展示如下問題情境：某藥店新進一批消毒液，每瓶的進價為10元，在銷售中發現銷售量y（瓶）和每瓶銷售價x（元）存在一次函數關系（其中10≤x≤21且x為正數），當售價定位12元時，每天銷售量為90瓶;當售價定為15元時，每天銷售量為75瓶.若每天的銷售利潤為w元，則售價定為多少元時，每天獲得的利潤最大？

解答：該題先構建銷售量y和售價x的函數模型，而后構建每天利潤和售價的函數模型.根據題意可知y=kx+b，根據已知條件不難求出k=-5，b=150，y=-5x+150，則w=（x-10）（-5x+150）=-5x2+200x-1500（10≤x≤21且x為正數），由二次函數性質可得x=- b 2a =20時，w取得最大值500，即，每瓶的售價為20元時每天可獲得最大利潤500元.

二、講解相關例題

初中數學課本中講解有最短路徑問題，實際上該問題屬于“將軍飲馬模型”.講解該模型時注重給學生預留空白的時間，要求學生認真揣摩求解最短路徑的思路，實際能夠真正的頓悟、理解與掌握.同時，為更好的鍛煉學生的學以致用能力，完成該模型的講解后為學生講解經典的例題，進一步拓展其視野，更好的把握“將軍飲馬模型”的本質，在以后的解題中能夠以不變應萬變.例如，在課堂上為學生講解如下例題：

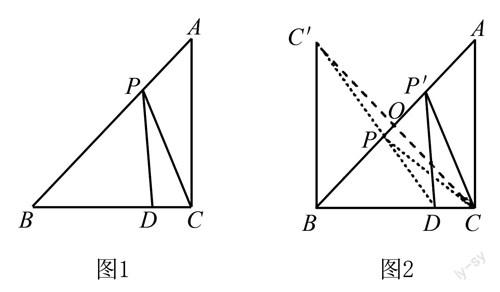
如圖1，△ABC為等腰直角三角形，其中∠ACB=90°，AC=BC，點D為BC上一點，BD=6，DC=2，點P為AB上一動點，則PC+PD的最小值為（）

A.8?? B.10?? C.12?? D.14

從“將軍飲馬”模型中獲得解題啟發，如圖2，過點C作CO⊥AB于點O，延長CO到C′，使得OC′=OC，連接DC′交AB于點P，連接CP.易知CP=C′P，∴PC+PD=C′P+PD，顯然當C′、P、D三點處在同一條直線上時其之和最小.連接BC′，則由對稱性可知∠C′BA=∠CBA=45°，∴∠CBC′=90°，則BC′⊥BC，∠BCC′=∠BC′C=45°，BC=BC′=8，由勾股定理可得DC′= BC′2+BD2 =10，選擇B項.

三、加強專題訓練

初中數學教學中為使學生更好的掌握建模思想的應用技巧，應結合學生的具體情況，以及數學模型的重要程度，積極組織學生加強相關的專題訓練活動.通過訓練使學生不斷的犯錯、糾錯，加深對數學模型的認識與理解，提高運用模型思想解題的效率.如在講解反比例函數知識時，引導學生關注如下模型：如圖3所示，在y= k x 上存在一點A，過點A作AB⊥x軸與點B，則S△AOB= k 2 .該模型是初中數學各類測試以及中考的參考模型，教學中可引導學生自行推導該模型的結論，與此同時向學生展示如下習題，及時對學生進行訓練，使學生能夠當堂掌握該模型：

如圖4，點A為反比例函數y= 6 x 的圖象上一點，過點B作AB⊥x軸，垂足為B，線段AB和反比例函數y=?2 x 的圖象交于點C，則△AOB的面積為（? ）.

A.4?? B.3?? C.2?? D.1

本題在在模型的基礎上有所延伸，能很好的考查學生對模型的理解程度.實際上，S△AOC=S△AOB-S△OCB，由模型中的結論可很快的計算出=S△AOB= 1 2 ×6=3，S△OCB= 1 2 ×2=1，∴S△AOC=3-1=2，選擇C項.

四、重視學習總結

初中數學教學中為使模型思想更好的融入到教學之中，應注重引導學生學會學習，鼓勵學生做好學習的總結與反思，通過對常見問題的提煉與抽象，自行推導相關數學模型，并在解題中加以應用.同時，能夠主動的與其他學生交流學習心得，學習他人總結出的數學模型，更好的提高自身的解題能力.二次函數圖象的平移是初中數學的重要知識點，教學中引導學生進行總結，推導相關的模型，指引其以后更好的解題.在教師的指引下，學生總結出了如下模型：對于二次函數y=ax2+bx+c（a≠0）先轉化為頂點式y=a（x+h）2+k，其圖象沿著x軸平移m個單位，沿著y軸平移n個單位得到的函數解析式為y=a（x+h+m）2+k+n，其中沿x軸分別向左、向右平移時，m分別取正、負;沿y軸分別向上、下右平移時n分別取正、負，簡稱“上加下減，左加右減”.另外，點的平移也遵循該規律.為使學生體會到應用該模型解題的便利，可要求學生應用推導的模型解答如下習題：

將一段拋物線y=-x2+3x（0≤x≤3）向右平移9個單位，得到新拋物線和直線y=x+b有唯一公共點，則b的取值范圍是 .

根據總結的平移模型，由y=-x2+3xy=-（x- 3 2 ）2+ 9 4 ，由平移模型可知新得到的函數解析式為y=-（x- 3 2 -9）2+ 9 4 =y=-（x- 21 2 ）2+ 9 4 （9≤x≤12），將其和直線y=x+b聯立，令Δ=0，得到b=-8.同時，觀察平移后的圖象可求得b的取值范圍為-12≤b<-9.綜上b的取值范圍為b=-8或-12≤b<-9.

模型思想是一種重要的分析問題的思想，在初中數學占有重要地位.實踐中為使學生更好的掌握模型思想，能夠具體問題具體分析，提高其應用模型思想學習的靈活性，掌握運用模型思想的解題技巧，可按照理論的剖析、例題的講解、習題的訓練、學習總結這一思路開展教學工作，實現模型思想與初中數學教學活動的有效融合.

參考文獻：

[1]歐瓊華.初中數學教學中融入模型思想的策略[J].名師在線，2021（18）：66-67.

[2]黃屹東.融入模型思想 優化初中數學教學[J].新智慧，2021（01）：91-92.

[3]龔華敏.論數學模型思想在初中數學教學中的滲透[J].數理化解題研究，2021（11）：30-31.

[4]莫宇平.應用模型思想提高學生數學應用能力探研[J].成才之路，2021（11）：58-59.

[5]邱宗如.初中數學模型思想的教學實踐與思考[J].福建中學數學，2020（08）：43-45.

[責任編輯：李 璟]