傾轉旋翼無人機動力學建模與控制系統設計

劉建龍，竇銀科，左廣宇

(太原理工大學 電氣與動力工程學院，山西 太原 030024)

0 引言

近年來無人機技術水平不斷發展，為提高無人機性能，垂直起降無人機逐漸成為無人機研究領域內的熱點問題之一。作為垂直起降無人機的一種方案，傾轉旋翼無人機受到廣泛的關注。傾轉旋翼無人機是在四旋翼無人機的基礎上，將飛行方向的前兩個旋翼增加傾轉舵機實現由垂直方向向水平方向上的傾轉。美國波音公司和貝爾直升機公司(Boeing Bell)聯合開始研發的“魚鷹”號無人機最早實現這種傾轉模式[1]。這種無人機的飛行模式分為3種模態：固定翼模態、傾轉過程模態與四旋翼模態。四旋翼模態可以使無人機進行垂直起飛與降落，減少傳統固定翼無人機起飛所需要的空間；固定翼模態可以進行高效率遠距離的航行；傾轉過渡模態是這兩種模態的銜接過渡過程[2]。

本文對四旋翼的傾轉旋翼無人機任務模式分析并進行了動力學建模。通過拉力實驗得到了模型中常系數。通過對傾轉過程的研究，規劃傾轉過程控制策略，并為此設計了控制電路，使得飛行器的可以在預定時間內完成傾轉過程。

1 動力學建模

為便于對無人機飛行狀態的研究，本文將引入兩個基本坐標系：地球表面慣性坐標系與機體坐標系。利用地面慣性坐標系e研究了無人機相對于地面的運動狀態，確定了機體的空間位置坐標。假設地球表面是一個平面，在地面上選一點Oe作為無人機的起飛位置[3]。Xe軸在水平方向上，Ze軸垂直于地面向下，確定Ye軸的右手坐標系為地理坐標系。機體坐標系b，其原點Ob取在飛行器的重心上，機體坐標系與飛機固連(通過將傳感器固定在飛行器上，采用數學算法確定出機體坐標系)。Xb軸正方向指向機頭方向(機頭方向與多旋翼“+”字形或“X”字形相關)，Zb軸垂直Xb軸向下，最后確定Yb軸的右手坐標系。

通過繞3個坐標軸旋轉歐拉角φ、θ、ψ 將地球表面慣性坐標系轉動到機體坐標系，3次轉動可以用數學方法表述成3個獨立的方向余弦矩陣，定義如下。

從地理坐標系到機體坐標系的變換矩陣為：

式中，φ 表示旋轉過程中自轉角大小。

從地球表面慣性坐標系到機體坐標系的變換矩陣為：

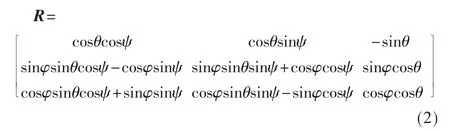
式中，θ、ψ 分別表示旋轉過程中章動角、進動角大小。

傾轉旋翼無人機控制邏輯用于控制傾轉旋翼無人機3個關鍵的飛行模態：垂直起降、傾轉模態以及固定翼模態[4-5]。飛行任務流程如圖1所示。

圖1 全模態自主飛行流程圖

起飛階段，無人機為四旋翼模態，通過調整油門使4個螺旋槳轉速變快，拉力變大。當拉力大于重力時無人機完成垂直起飛。起飛后無人機可以在此模式下進行低速巡航。當無人機達到指定高度后，利用四旋翼進行無人機懸停。此后接受傾轉指令，無人機的前兩個傾轉舵機進行傾轉，拉力沿水平方向上的分力使得無人機具有前飛加速度，前飛速度變大。拉力垂直方向上的分力減小，需要提供更大轉速而獲得更高的拉力來平衡重力。待無人機完成傾轉過程后，進入固定翼模態。此時啟動無人機副翼舵機與V型尾翼舵機進行姿態控制，無人機可以進行高速度、遠距離的巡航與觀測。巡航任務完成后，無人機需要進行一個逆傾轉過程，此過程與傾轉過程是對偶的。傾轉舵機由水平方向向垂直方向進行傾轉，拉力的垂直方向分力逐漸變大，平衡重力所需要的拉力逐漸減小。則轉速控制變慢，拉力的水平分方向力減小，加速度減小，由空氣阻作用，前進速度也逐漸降低。無人機在完成逆傾轉過程后，轉變為四旋翼模態，降低油門可以進行垂直降落。傾轉過程與逆傾轉過程需要進行準確的控制。傾轉時間上的控制也尤為重要。在不同模態下，控制模式不同，控制模式總結如表1所示。

表1 不同模態下的控制模式

在不同模態下，傾轉旋翼無人機控制策略與方法不同，其力與力矩的執行單元也不同。圖2為傾轉旋翼無人機在傾轉過渡過程中受力示意圖。

圖2 傾轉過渡過程中受力分析示意圖

傾轉過程中穩態時，受力關系如下：

其中，重力加速度g=9.8 m/s2，a為飛機前飛加速度，T1、T2、T3、T4分別表示4個槳葉提供的拉力，Ω1、Ω2、Ω3、Ω4分別表示4個槳葉的轉速，δ1、δ2表示傾轉槳葉與飛機前飛方向夾角。

無人機的主要動力來源是槳葉旋轉提供的拉力。對于槳葉提供的拉力大小常用葉素法分析，將槳葉沿徑向分為無限個微小的片段，每一個微小片段均被等效成一個小型固定翼葉片，并推導其升力大小，即計算每一個葉素上的氣動力，最后將這些葉素上的氣動力積分求和，得到該槳葉的總氣動力大小[6]。

葉素升力求解公式為：

其中，c為葉片弦長，q為動壓，Δr為葉片截面的微分。CTe是葉素升力系數，為迎角α 的函數；Ti為葉素產生的拉力大小。

其中，ρ 為來流空氣密度，Ve為葉素速度大小。

積分求得：

即Ti=KTΩ2，其中升力系數：

式中，Ω 為葉片旋轉的角速度，R為葉片半徑，Kα為失速前葉素升力系數與迎角之間的線性系數，θt為葉片安裝角，φt為葉片入流角。

2 模型參數測量

利用SolidWorks對無人機進行模型分析，得到無人機得準確數據[7-9]。由于電池與控制模塊的放入，使得重心不能以軟件輸出的結果為準，本文采用三線法測量無人機的重心：在無人機上選取3個任意點，用懸線將其拉起，待機機體穩定后，記錄懸線及其延長線位置，3條懸線交點即為重心位置。在不同模態下無人機重心測量結果表明，重心位置基本重合，所以可以忽略傾轉舵機的位置變化對重心位置的影響。對于電機與槳葉組合的拉力系數和電機、舵機的響應特征需進行實驗測量。

2.1 旋翼拉力系數測量

由前面分析可知，旋翼產生的拉力大小Ti和力矩與轉速Ω(弧度每秒)的平方成正比，即：

本小節對該模型中系數KT行測量。采用非接觸光電式轉速計進行轉速測量。轉速計(VICTOR 6234P)的準確度為±(0.5%+5)。采用Mayatech MT10PRO航模槳葉測試專用拉力計進行拉力的測量，量程為0～10 kg。通過在STM32單片機開發板編寫程序對旋翼轉動時的PWM生成與時間進行記錄，利用安捷倫E3632A穩壓電源提供電機的直流電能，并記錄電流值，從而通過擬合得到相關系數，實驗裝置結構如圖3所示。

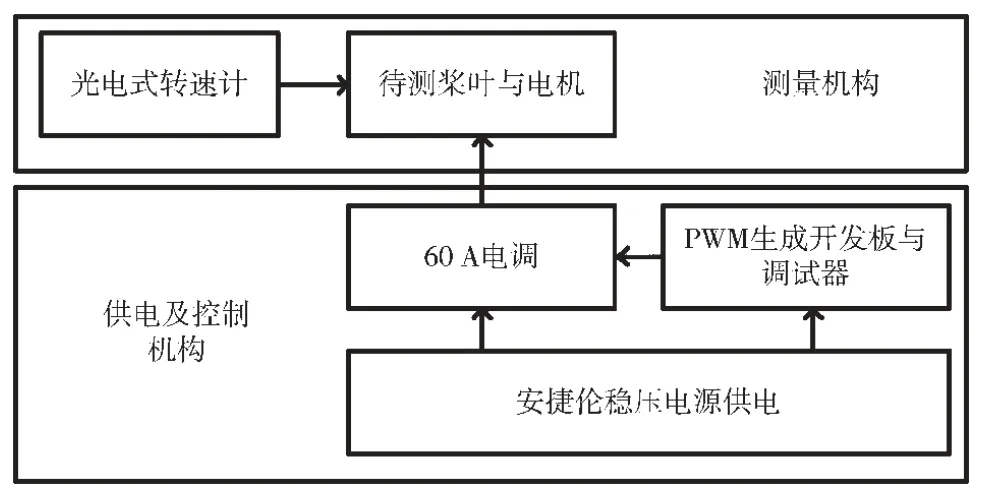
圖3 拉力試驗平臺布置圖

實驗過程：將穩壓電源調至6S電池供電(即22.2 V供電電壓)。通過調節開發板程序，改變PWM脈沖時間。在不同的PWM脈沖時間采集轉速、拉力數據及對應變化時間。考慮轉速計和拉力計的量程范圍，PWM的脈沖時間設置為由1 ms逐步增加到1.5 ms。為減小由震動對測量結果的影響，每次測量均讀取超過10 s后的穩定拉力數據，且利用多次測量求取平均值的方法減少測量誤差。拉力計讀數Ti與轉速平方的擬合結果如圖4所示。測量出的坐標點均勻地分布在擬合結果兩測，驗證了葉素法的分析結果的準確性。通過擬合得到的關系式如下：

其中，Ω 為轉速大小，單位為r/min。

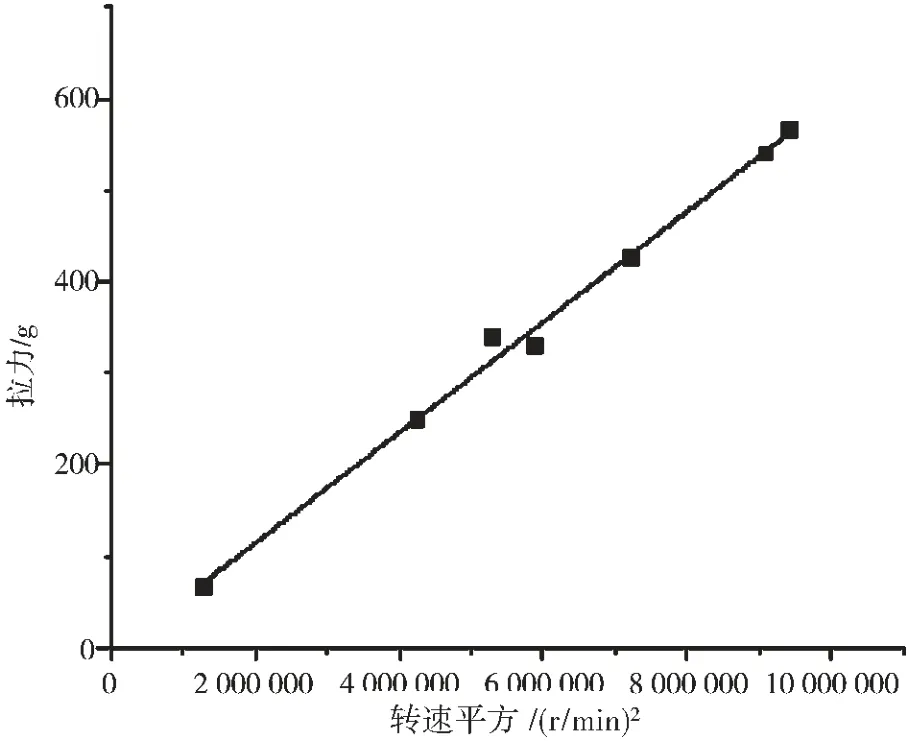
圖4 擬合結果圖

2.2 電機和舵機響應特性測量

電機的響應特性可以近似為[10]：

其中，Ωc為旋翼的轉速期望；kw為轉速變化系數，kw的大小與電機的響應速度成正相關。對于kw采用系統辨識法進行辨識測量[11]。對待測電機施加1 150 r/m的階躍響應信號，記錄轉速與到達該轉速所用時間。在MATLAB中的系統辨識工具箱(System dentification)進行辨識[12]，擬合結果如圖5所示。

圖5 電機轉速響應

由辨識結果得響應特性為：

其他執行機構響應特性(如舵面的舵機和傾轉機構的舵機可以選用的舵機參數)用一階慣性環節近似。副翼與尾翼舵機的響應特性近似結果為：

傾轉機構舵機的響應特性近似結果為：

3 系統硬件電路設計

為使無人機的3種模態得以確定，需要10路PWM信號來控制電機和舵機的運動。因此選用兩片STM32單片機進行控制，其中主單片機進行算法與飛行姿態信息的解算[13]，并對4個旋翼電機進行PWM信號輸出與控制。協處理器主要是對慣性監測單元MPU6050模塊的數據進行采集，并完成對6個舵機的PWM信號輸出與控制[14]。系統電路結構圖如圖6所示。

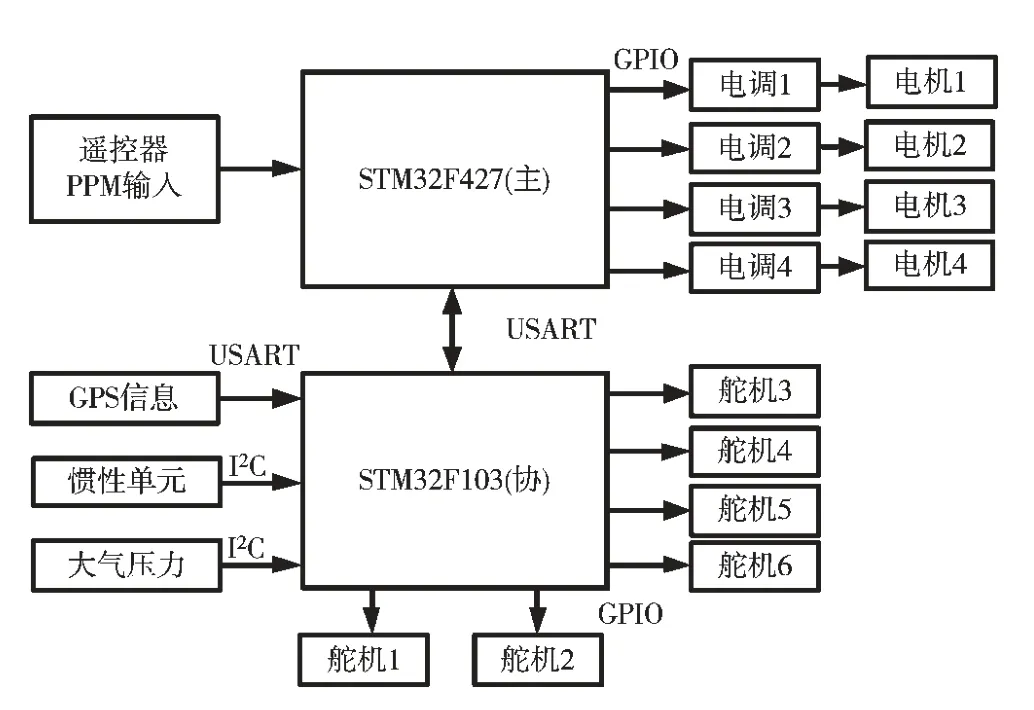
圖6 系統電路結構電路圖

無人機選擇6S-Li電池，經計算電壓為22.2 V～25.2 V。由于舵機需要5 V供電，單片機需要3.3 V供電，因此要對電源進行DC-DC降壓處理。分別采用LM2596與LT11293作為降壓IC[15-17]，電路原理圖如圖7所示。

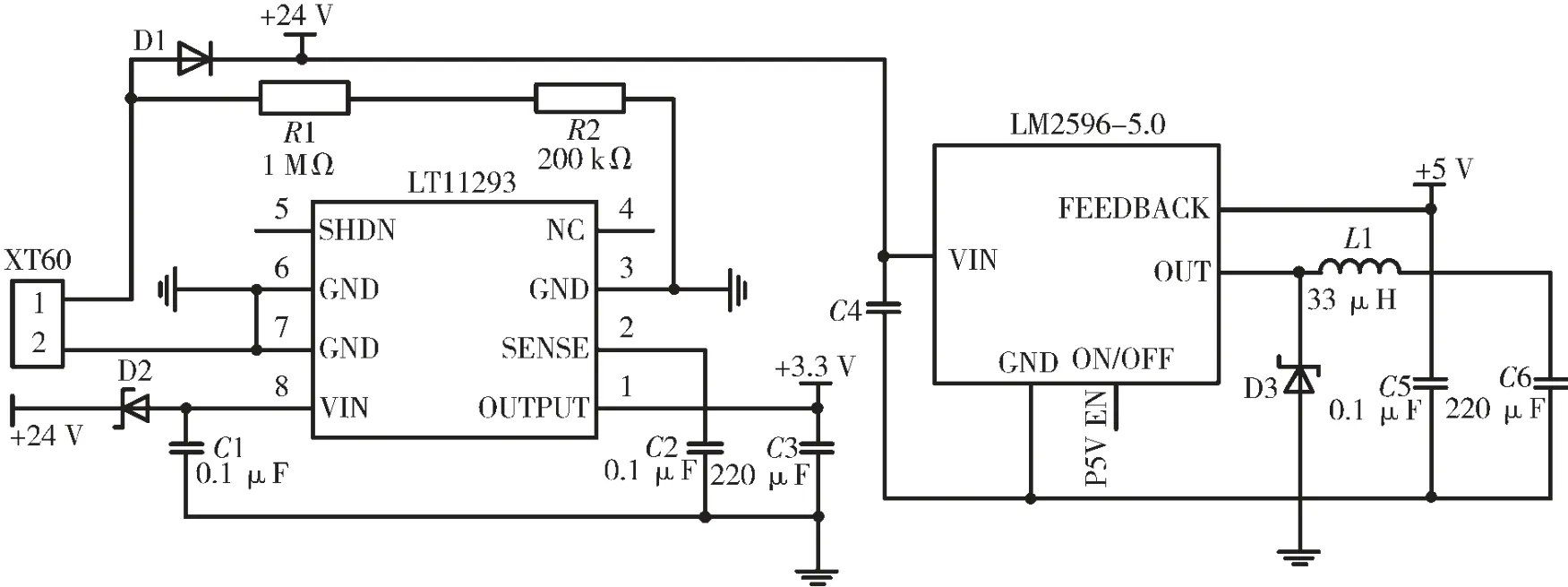
圖7 電源部分原理圖

4 傾轉過程控制策略

在傾轉四旋翼無人機過渡態飛行模式中，傾轉舵機由垂直方向傾轉至水平方向，槳葉提供的拉力在水平方向的分量隨著傾轉過程變大，由牛頓第二定律，可以確定無人機的前飛速度也在增大，則機翼提供的升力也變大。拉力的垂直方向上的分量隨著傾轉角的變化逐漸變小。為保證過程的平衡，對傾轉角變化速度進行控制[18]。由前二部分分析結果式(3)、式(9)計算得出傾轉過程中轉速、拉力以及前行速度之間的關系，即傾轉走廊。

依據選取的舵機轉速范圍[19]，本文設計過渡過程中傾轉舵機可以進行21 deg/s的勻速轉動。為保證可以平滑地進行轉動，在傾轉的開始后與結束前進行線性的增加或減小。為保證設計結果的性能要求，傾轉過程保證在5 s內完成。本文設計轉速Ω 與時間t的關系為：

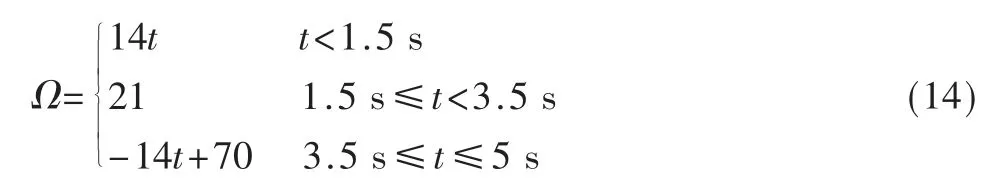
通過對傾轉角轉速變化規律積分可以得到傾轉角變化規律，其中兩個傾轉角δ 保持時刻相等，即：

由于前行速度與傾轉舵機角度之間的制約關系，需要對傾轉過程控制回路進行設計。回路結構如圖8所示。

圖8 傾轉控制回路

5 樣機測試實驗

傾轉測試實驗首先將遙控器的油門進行校準，校準結果為最大舵量2 015 μs(即PPM信號中油門通道脈沖時間)，最小舵量991 μs。供電后通過遙控器通道5進行模式切換，傾轉電機進行傾轉。改變油門大小進行反饋測試，記錄傾轉過程時間。實驗數據如表2所示。

表2 空載傾轉實驗時間數據

由表中數據可以驗證空載時，電機轉速全范圍都可以控制傾轉時間小于5 s，完成規劃要求。

對于傾轉控制反饋回路，測試現象如下：減小油門，傾轉舵機傾轉角變小；抬高油門，傾轉舵機傾轉角變大。同時對固定翼副翼提供的姿態調節反饋進行測試，手動改變無人機姿態，無人機各翼提供相應的舵量控制。

6 結論

傾轉四旋翼無人機結合了四旋翼無人機與固定翼飛機的優勢，它可以在很多不宜小型四旋翼無人機飛行的環境下進行巡航任務。這種無人機也來越來越受到重視，在這樣的背景下，本文設計出一款傾轉四旋翼無人機，完成對傾轉時間的穩定控制。經過對傾轉旋翼無人機的運動學建模，確定控制量以及所需要的力學參數。并且通過實驗完成旋槳拉力系數、電機的響應特性的系統辨識。同時，本文完成了電路結構的設計，并對傾轉過程控制反饋的調節。樣機測試實驗表明，本文設計的結構可以完成規劃時間內的傾轉，并有穩定的反饋效果。