改進WOA的單液流鋅鎳電池充電策略
宋春寧,莫偉縣,蘇有平
(廣西大學電氣工程學院,廣西 南寧 530004)
目前的電池充電優化技術,主要以縮短充電時間、降低能量損耗等目標為主[1],而影響的因素主要是充電電流。充電電流過大,雖然能縮短充電時間,但充電時的能耗也隨之增大,反之亦然。孫志昆[2]設計了100階段的充電策略,以充電時間與溫升為優化目標,雖然能縮短充電時間、降低溫升,但并未考慮環境溫度的影響。陳亞愛等[3]為解決鉛酸電池充電時的極化現象,提出一種基于馬斯曲線的快速充電控制策略,用實驗驗證了提出的充電控制策略能實現快速充電,且不影響鉛酸電池的使用壽命。單液流鋅鎳電池與雙液流電池相比,只需要一個儲液罐和一個電機,不需要昂貴的離子交換膜,具有循環壽命長、安全性能好、制造和維護成本較低、使用方便和無記憶效應等優點。研究該電池的充電過程,具有一定的意義。
鯨魚優化算法(WOA)[4]是一種群體智能優化算法,在迭代計算過程中模仿座頭鯨群體的捕食行為,來尋找目標問題的最優解。由于它的最優個體及運動方式依概率更新,具有更大的隨機性和更快的收斂速度。黃清寶等[5]在WOA基礎上提出了基于余弦控制因子和多項式變異的鯨魚優化算法,有更快的收斂速度及收斂精度;O.Diego等[6]提出了一種混沌鯨魚優化算法(CWOA),利用混沌變異增強算法跳出局部最優解的能力;王廷元等[7]提出一種基于自適應策略的混合鯨魚優化算法,利用蝙蝠算法的局部搜索機制,達到增強種群多樣性、避免過早陷入局部最優的目的,提高了收斂速度和尋優精度。
本文作者建立時間-能耗模型,并提出改進的WOA對電流值進行優化,實現對單液流鋅鎳電池的充電控制。
1 單液流鋅鎳電池時間-能耗模型的建立
1.1 單液流鋅鎳電池等效模型的建立
電池用的主流等效電路模型有電化學模型、內阻(Rint)模型、阻容(RC)模型、Thevenin模型和新一代汽車合作伙伴(PNGV)模型等。鋅鎳液流電池內部的化學反應復雜,采用電化學模型不利于分析與計算;內阻模型過于簡單,只考慮一個電壓源與一個內阻,不能很好地對鋅鎳液流電池內部反應進行描述;PNGV電路模型與RC模型,雖然能較好地描述鋅鎳液流電池內部反應,但存在計算復雜的問題。
綜合模型精度和計算復雜程度考慮,選用Thevenin模型,為后面對電池的建模、辨識參數及SOC估算提供基礎,模型如圖1所示。
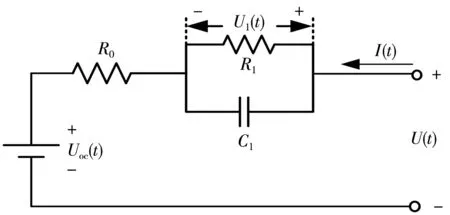
圖1 電池的Thevenin模型
圖1中:Uoc是開路電壓(OCV);R0是歐姆內阻;R1、C1分別是極化電阻與極化電容;U是電池兩端的電壓;U1是極化電容兩端的電壓;I是充電電流值,箭頭方向是電流方向;t是時刻。此外,模型還考慮了開路電壓隨SOC的變化[8]。
1.2 單液流鋅鎳電池等效模型的參數辨識
根據圖1的電池Thevenin模型與基爾霍夫電壓定律、基爾霍夫電流定律,得到辨識參數,滿足關系式:
(1)
為了辨識電池的參數,可通過混合動力脈沖能力特性(HPPC)中脈沖充電曲線得到模型參數R0、R1與C1,單步脈沖充電曲線如圖2所示。

圖2 單步脈沖充電曲線
在圖2中,B點電壓為UB、A點電壓為UA;A-B階段電壓變化由歐姆內阻R0引起;B-C階段電壓變化由R1和C1組成的RC電路的零狀態響應引起;C-D階段電壓變化是因為充電電流撤走的緣故;D-E階段電壓變化由R1和C1組成的RC電路的零輸入響應引起;對應的零輸入響應和零狀態響應分別見式(2)與式(3),其中R1和C1組成的RC一階電路的時間常數τ見式(4)。
U1=U1(0)e-t/τ
(2)
U1=IR1(1-e-t/τ)
(3)
τ=R1C1
(4)
式(2)-(3)中:e為自然常數。
根據圖2所得,對應的歐姆內阻按式(5)計算。
(5)
在D-E階段,根據式(2)通過MATLAB的cftool工具箱擬合計算,得到τ;在B-C階段,根據式(3)及式(2)得到τ,然后擬合計算,求得極化電阻R1,再由式(4)得到極化電容C1,由此可得到電池不同SOC對應的R0、R1、C1及τ。參數可為后續建立時間-能耗模型提供數據基礎。
實驗用單液流鋅鎳電池的尺寸為40 cm×20 cm×60 cm,額定容量Cn為8.5 Ah,制備時的環境溫度為 25 ℃,電解液的體積為2.0~3.0 L,其中氫氧化鉀(張家口產,95%)濃度為10.00 mol/L,氧化鋅(張家口產,99.5%)濃度為0.80 mol/L、氫氧化鋰(張家口產,98%)濃度為0.25 mol/L;正極材料是氧化鎳(智電芳華蓄電研究所提供)、負極材料是鍍鋅電極(智電芳華蓄電研究所提供)。用CT-3004-5V200A-NTFA電池綜合測試柜(武漢產)進行測試。
1.3 單液流鋅鎳電池的SOC與OCV曲線
單液流鋅鎳電池的OCV與SOC具有函數關系,電池靜置60 min后,極化電壓U1衰減至接近0 V,此時端電壓等于OCV。通過脈沖充電曲線可得到OCV與SOC的數據,再結合6次多項式擬合,得到式(6)的關系式:
Uoc=a0S6+b0S5+c0S4+d0S3+e0S2+f0S+g0
(6)
式(6)中:S是SOC,a0=-6.971、b0=23.74、c0=-32.06、d0=22.06、e0=-8.341、f0=1.833、g0=1.598。
1.4 時間-能耗模型建立
在建立時間-能耗模型前,將整個SOC(0~95%)每隔5%進行劃分,分為N(N=19)個階段,對應N個電流值對單液流鋅鎳電池進行分段恒流充電,電流為0.2~1.5C;選用最終SOC為95%是為了防止過充和排除上限電壓的影響;選用間隔5%、分N個階段,是因為充電的時間與電流大小有關,而產生的能耗與電流大小、歐姆內阻、極化內阻及極化電壓有關。歐姆內阻、極化內阻及極化電壓隨SOC的變化而變化,通過間隔SOC進行分階段充電,能更精準地描述產生的能耗;該模型輸出的是充電產生的總能耗與總時間。
1.4.1 時間模型
分段恒流充電是每個階段以不同電流對單液流鋅鎳電池進行充電,通過累加每個階段的充電時間,得到單液流鋅鎳電池充電過程的時間模型,所對應的關系式見式(7)。
(7)
式(7)中:ttotal是整個充電過程的總時間;ΔQ是每個階段充入的容量,即0.05×Cn;Ix是每個階段的電流值。
1.4.2 能耗模型
對于所采用的Thevenin模型,能耗主要是由歐姆內阻R0及極化電阻R1產生,關系式見式(8)。
(8)
式(8)中:Eloss是充電過程中總能耗;Icharg是充電電流;R0與R1隨著SOC變化而變化。
令Icharg[k]=Icharg[kΔt],U1[k]=U1[kΔt],假設kΔt到(k+1)*Δt時刻電流保持不變,則對式(8)進行離散化可得到式(9):
(9)
據式(9)所得,充電產生的能耗與分段電流值Icharg[k]、R0、R1和U1有關,而后三者與SOC有關,且隨SOC動態變化,可以根據參數辨識得到對應的參數值。
2 SOC的估計與鯨魚優化算法
2.1 擴展卡爾曼濾波(EKF)估計SOC
卡爾曼濾波算法是一種線性系統最優估計算法,最優值是由“預測值”+“修正”得到,但單液流鋅鎳電池是一個非線性系統對象,因此卡爾曼濾波不能直接用于該對象。擴展卡爾曼濾波(EKF)是在卡爾曼濾波的基礎上,對非線性模型進行一階Taylor級數展開,只考慮一次項,不考慮高次項,在非線性對象的展開點附近被近似線性化,從而使用卡爾曼濾波。
對于EKF的系統狀態空間如式(10)所示:
(10)
式(10)中:x是狀態向量;y是觀測量;f、g都是非線性函數;w、v分別是過程噪聲與測量噪聲。
根據式(1),選取[S(k),U1(k)]T作為系統狀態變量,端電壓U作為輸出量。基于Thevenin等效電路模型的一階Taylor級數展開EKF離散狀態空間方程,見式(11)。
(11)
式(11)中:ts是系統采樣時間,一般ts=1 s;η是庫侖效率,此處假定為1;Ik是充電電流。
2.2 鯨魚優化算法
2.2.1 基本鯨魚優化算法原理
鯨魚優化算法是模仿座頭鯨魚氣泡網攻擊捕食行為的一種啟發式優化算法,在群體捕食過程中,個體所處的坐標將作為問題的一個解,最優個體的位置即為最優解。該算法包括3個階段:包圍獵物、氣泡網攻擊和尋找獵物。
①在包圍獵物階段,數學模型如式(12):
X(iter+1)=X*(iter)-a(2r-1)|2rX*(iter)-X(iter)|
(12)
式(12)中:iter代表當前算法迭代次數;X、X*分別代表當前解和目前最佳解;r是[0,1]中的隨機向量;權重a隨著iter的增加,從2線性減小到0。
②在氣泡網攻擊階段,數學模型如式(13):
X(iter+1)=|2rX*(iter)-X(iter)|eblcos(2πl)+X*(iter)
(13)
式(13)中:b為常數;l是[0,1]隨機向量;π是圓周率。
③在尋找獵物階段,數學模型如式(14):
X(iter+1)=Xrand(iter)-a(2r1-1)|2r2Xrand(iter)-X(iter)|
(14)
式(14)中:Xrand表示鯨魚從種群中隨機選擇一個個體作為目標位置;r1,r2是[0,1]的隨機數。
在WOA中,當控制參數A=|a(2r-1)|<1時,進行局部搜索,此時,鯨魚以0.5的概率來包圍獵物,以0.5的概率來進行螺線運動;當控制參數A>1時,算法進行全局探索。
2.2.2 一種改進的鯨魚優化算法
權重a是線性減小的,即算法全局探索能力線性減小,局部搜索的能力線性增強。為增強算法的全局探索能力,避免算法過于早熟,黃清寶等[5]提出了一種改變參數a的方法(記為f1WOA),將a改為按照余弦曲線變化,使得a在算法迭代前期較大并緩慢減小,以充分進行全局探索,在算法迭代后期急速減小,以進行局部搜索。
在余弦曲線變化的基礎上,本文作者提出一種改進的方式(記為f2WOA),增加了隨機性,如式(15)所示。
(15)
式(15)中:itermax是最大迭代次數500;r3是[0,1]的隨機數;k1、k2是[0,1]的數,且k1+k2=1。
當k1=0.3、k2=0.7時,權重a與迭代次數的關系如圖3所示。

圖3 權重a與迭代次數iter的函數關系曲線
從圖3可知,在算法迭代后期,且此時適應度值的變化幅度比較小時,a能獲得較大的權重,能增強算法的全局搜索能力,較好地跳出局部最優。
2.2.3 鯨魚優化算法目標函數的建立
時間-能耗模型輸出的是總時間ttotal、總能耗Eloss。當電流值大時,充電時間就短,充電過程能耗就高;電流值小時,充電時間就長,對應的能耗就低。這是兩個相互矛盾的問題,因此對兩個問題進行優化,是雙目標優化問題。在雙目標優化問題上,吳字強等[9]提出了一種針對燃料電池系統穩態輸出功率與效率的優化算法,實現對輸出功率和效率的最優化。對于雙目標優化,常用的方法是權重系數變化法,實驗用該方法將雙目標優化問題轉化為單目標優化問題[2]。
根據時間-能耗模型,優化0~95%SOC的電流值。在這個SOC范圍內,對充電時間與充電過程的能耗進行整體優化,則單液流鋅鎳電池的目標函數如式(16):
Objective=αEloss+βttotal
(16)
式(16)中:α、β分別是能耗權重與時間權重,整個充電過程中,電流值不同,產生的能耗Eloss與充電時間ttotal也不同;Objective是時間能耗-模型的適應度。
因為Eloss、ttotal的單位不同,數量級也不相同,無法進行比較,并且會在后面計算適應度時產生偏差,無法得到準確結果,所以要對兩個目標值進行歸一化處理。常用的歸一化方法有最大-最小標準化、Z-score標準化和函數轉化等[10]。本文作者采用最大-最小標準化方法,但未將一個數值映射到[0,1],而是映射到[0,100]的區間,以便于比較。目標函數變換成式(17):

(17)
式(17)中:Emax、tmax是每個階段電流取值最大(1.5C)時對應的充電產生的總能耗與充電所用總時間;E0.2 C、t0.2 C是每個階段電流取值最小值(0.2C)時對應的充電產生的總能耗與充電所用總時間。Obj是目標函數變換后時間能耗-模型的適應度。
3 仿真與分析
3.1 改進的鯨魚優化算法仿真分析
采用4個標準測試函數的shifted型進行仿真實驗[5],分別為F1(shifted Sphere)、F2(shifted Quartic with noise)、F3(shifted Rosenbrock)和F4(Shifted Ackley),測試改進鯨魚優化算法(f2WOA)的求解能力。所有仿真實驗在PC上運行,程序為Matlab 2014a的M腳本語言。測試函數見表1。

表1 4個標準的偏移型測試函數
表1中:xi是函數解x的第i維量的值;oi是偏移量o的第i維量的值;zi是過程變量。
將改進的鯨魚算法(f2WOA)與基本的鯨魚優化算法(WOA)、余弦變化的鯨魚算法(f1WOA)進行比較。實驗設置為:種群規模N=50,最大迭代次數為50 000次,偏移量oi(i=1,2,……,n)為搜索范圍內的隨機值。3種算法分別對每個測試函數獨立運行30次,記錄算法求得的最優函數值的平均值(Ave)和標準差(Std),其中平均值反映了算法的求解精度,標準差反映了算法的求解穩定性,運算結果見表2。

表2 測試函數優化結果對比
從表2可知,在求解精度及穩定性方面,改進的鯨魚優化算法(f2WOA)要優于WOA與f1WOA。
3.2 算法(f2WOA)求解時間-能耗模型仿真分析
為了驗證該方法(f2WOA)能否達到優化目的,采用文獻[11]中恒流恒壓方法中的0.5C恒流充電方式進行實驗對比。實驗選擇的SOC是0~95%,即當SOC等于95%為充滿,電流值取值為1.70~12.75 A(0.2~1.5C)。選用改進的鯨魚優化算法(f2WOA)求得能耗權重α與時間權重β比重不同時,充電過程產生的能耗與所用時間,以及0.5C恒流充電產生的能耗與所用時間,結果見表3。

表3 不同α、β比及恒流充電產生的能耗與所用時間
從表3可知,當α∶β為9∶1~6∶4時,充電產生的能耗較少,但充電時間延長;當α∶β為4∶6~1∶9時,充電所用的時間縮短,但能耗增加。
將表3數據作圖,得到圖4,不同α、β比優化后的電流值列于表4。
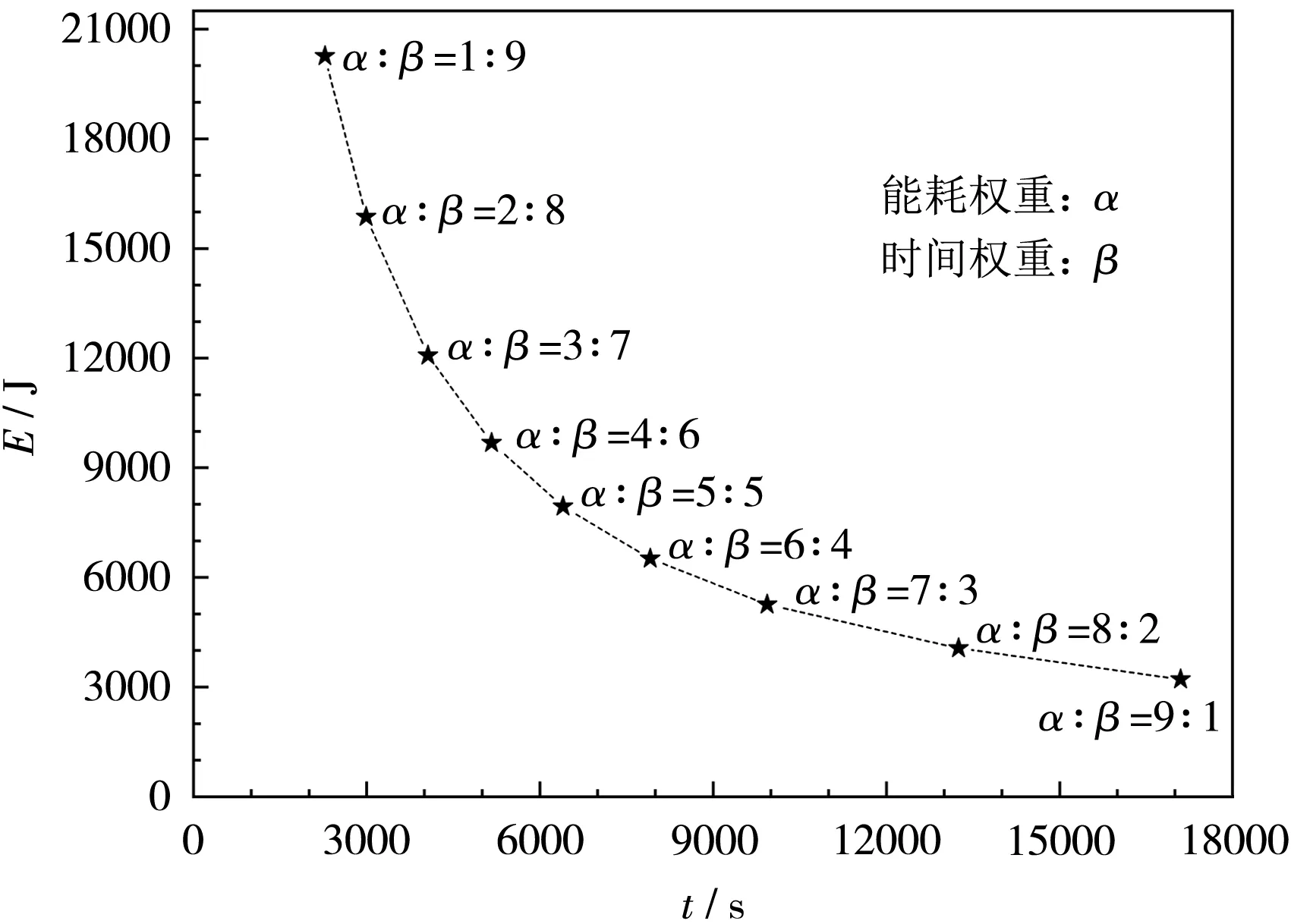
圖4 不同權重比優化結果

表4 不同α、β比優化后的電流值
從圖4可知,當能耗權重α占比較大時,優化偏重于能耗,所對應產生的能耗較短,但充電所用時間較長;當時間權重β占比較大時,優化偏重于時間,充電所用時間較短,但產生的能耗較多。這是兩個相互矛盾的指標,要根據不同側重點選用不同的能耗權重α、時間權重β比。
當α∶β=5∶5時,能耗較恒流充電少了125.8 J、時間縮短了145 s,即能耗減少了1.58%、充電時間縮短了2.27%。結果表明,通過SOC來進行分階段充電,以產生能耗和充電所用時間為目標進行優化,可以降低能耗及縮短充電時間。
4 結論
本文作者提出了改進的鯨魚優化算法(f2WOA),在求解復雜問題上與余弦變化的鯨魚算法(f1WOA)、基本的鯨魚優化算法(WOA)相比,有較優的求解精度及穩定性。通過脈沖充電實驗,辨識得到電池的具體參數,建立時間-能耗模型,使用改進的鯨魚優化算法(f2WOA)優化該模型。仿真分析結果表明:通過分階段對單液流鋅鎳電池進行充電,采用優化后的電流值,較0.5C恒流充電能耗減少1.58%、充電時間縮短2.27 %。本文研究過程中,假定電池的參數不變,沒有考慮到電池受到老化及電解液流速的影響,在后續的研究中可考慮添加這兩方面的內容。

