基于EMD-HHT的地下淺孔爆破振動規律研究

張其虎，張 希，孫進輝，范天林

(1.昆明理工大學 國土資源工程學院，昆明 650093；2.玉溪礦業有限公司，云南 玉溪 653405；3.云南銅業股份有限公司礦山研究院，云南 玉溪 653405)

鑿巖爆破是地下礦山掘進過程中的重要施工手段，但其產生的爆轟波不可避免地對地表臨近建筑物的承載能力及穩定性帶來不利影響，礦山爆破的聲音、震動、爆破飛屑物等會給周圍環境帶來較大的影響，甚至會對周邊居民的日常生活造成嚴重的困擾[1-3]；而且爆破作業受到技術、資金等建設條件的限制以及環境、地質方面的更高要求，所以人們對爆破技術的要求越加苛刻[4-6]。又因為爆轟波是在水平面位置處以波的形式做往復運動，本身持續時間短以及波形傳播介質和賦存條件復雜多變，從而導致爆破地震的復雜性[7]。眾多研究者分別從理論研究、試驗驗證、破壞準則等方面研究爆破振動規律。雷明等[8]基于對爆轟波峰值速度的理論研究，分析了井下爆炸產生的應力波對圍巖區域的影響因素，從而對巖巷穩定性進行了評估。張家斌[9]利用統籌理論建立了東川嶺礦的爆轟波運動軌跡模型，以此來研究振動波的傳播規律。李宇星等[10]從爆破振動三要素的角度出發，基于爆破振動及波形傳播規律對周圍建筑物進行穩定性評估分析。邱賢陽等[11]將實測數據和數值模擬結合，得出具有現實意義的理論數值依據，用作周圍建筑物承載能力和穩定性的評判標準。梁升等[12]運用ANSYS/LS-DYNA數值模擬手段，分析爆破振動規律，為建構筑物提供安全穩定性的理論依據。結合國內外學者的研究成果[13-17]，筆者以金沙礦業官房礦段地下爆破作業為依托，對現場爆破作業過程中的實測數據信號進行采集，運用EMD-HHT分析法從爆破能量分布規律、爆破振動波形的頻譜特征、地震波衰減分析理論和爆破振動速度等方面進行研究分析。在爆破振動波形圖中可以得到質點的峰值振速及主振頻率等參量的數值大小，兩者都是與爆破振動效應相關的重要因素，峰值振速反映爆破荷載的大小，主頻率反映振動物的動態響應情況特征。基于對上述物理量對爆破振動波形的研究分析得到的相關結論，可為今后的地下淺孔爆破提供更為精確的研究思路和方法，指導地下礦山淺孔爆破作業。

1 EMD-HHT分析法

EMD-HHT分析法是根據實測數據本身的時辰維度進行頻譜分解，不再需要固定的先遣波形基底，利用Matlab對爆破振動波形數據信號進行EMD分解，通過編輯相應的程序語言在Matlab軟件上對波形數據運行處理，運行后會得到有限個不同的IMF分量，對去除噪音分量的IMF進行重構，將主要IMF分量進行Hilbert變換，得到能量分布圖譜即Hilbert譜，再進行Hilbert變換，最后提取出不同IMF分量的包絡幅值，并將頻率幅值分解為時頻譜、邊際譜、瞬時能量譜等，用以識別實際微差延期時間[18-20]。Hilbert時頻圖的表達形式為：

(1)

式中：Re—殘余分量r的實部；i—IMF的個數，i=1，2，3，…，n；ai、wi—常數；ai(t)—幅值函數；ωi(t)—頻率函數。

將H(ω,t)對時間積分，就得到Hilbert邊際譜：

(2)

再對Hilbert譜h(ω)的幅值利用積分計算方式對時間這個參量進行積分，最后通過求和可得Hilbert瞬時能量譜Es，其表達形式為：

(3)

對Es在頻域內積分可得到信號的Hilbert能量，其表達式為：

(4)

采用EMD方法對給定信號S(t)進行分解，最終原始信號S(t)可分解為若干IMF分量，每個IMF分量均為時間的函數ci(t)和一個余項rn(t)的和，即：

(5)

從式(5)中可以看出，將時間的函數ci(t)進行i=1到n的求和，即可得IMF分量c(t)，并將分量c(t)再一次進行Hilbert變換，即：

(6)

式中：PV—柯西主值，因此可以得到構造解析信號z(t)：

z(t)=c(t)+jH[c(t)]=a(t)ejΦ(T)

(7)

式中：a(t)—幅值函數；j—相關系數。a(t)為z(t)的幅值，也稱為信號包絡，其幅值函數為：

(8)

Φ(t)為相位函數：

(9)

2 爆破振動監測與信號分析

2.1 工程地質及爆破參數

PD207礦段為構造角礫巖型鉛鋅礦，礦體厚度約為1.0 m，其巖石物理力學性質如表1所示。選擇連續兩次的爆破作業振動監測結果進行分析。因礦體厚度較薄，采用淺孔爆破，采場回采作業孔深為2.5 m，炮孔直徑40 mm，孔距為1.0 m，排距0.8 m，炮孔不做填塞，炮孔采用梅花形布孔。第一次爆破總藥量29.2 kg，最大單響藥量4.8 kg；第二次爆破總藥量24 kg，最大單響藥量4.8 kg。采用磁電雷管加毫秒延期導爆管雷管的起爆方式，共布置了5個爆破振動監測點，分別放置4套TC-4850測振儀和1套BMView-8016測振儀。

表1 巖石物理力學性質

2.2 基于EMD-HHT法的信號處理及分析

選取BMView-8016所測得的數據來進行EMD-HHT分析，在分析過程中通常截取爆破振動波的垂直振動速度波形整體中的最大峰值振動段波形作為研究的對象，因為最大峰值處對應的最大瞬時能量即為最大能量荷載區域[21-23]。分別截取兩次典型的垂直方向通道的峰值振動段波形的兩組信號作為研究對象，記做A和B。

1)EMD-HHT分解

將已選擇好的兩次爆破作業振動監測結果的數據運用配套軟件將波形數據導出，在導出的波形圖中選擇波形峰值最大處，并將波形最大處所對應的數據轉為Excel文件格式導出，除去波形前后的數據和負延時所對應的信號數據。進而運用Matlab2018b數據處理軟件對導出的數據進行處理，然后運行出數據波形，再對得出的波形進行研究分析。從波形圖中可以得到12個分量以及殘余分量r，不同的IMF分量包含了不同的信號特征，從圖中可以看出，信號頻率是由高頻到低頻順序排列，在這些排列規律中可以發現A和B的各個IMF分量，如圖1和圖2所示。

圖1 A的IMF分量Fig.1 IMF component of A

圖2 B的IMF分量Fig.2 IMF component of B

從圖1和圖2中分析得出IMF1是速度和時間的關系，隨時間的變化速度變化頻率非常大，可以看出速度隨時間的變化較為明顯，從振動頻率幅值可以看出頻率變化最大，但占有的能量最小，從中可以分析出IMF1是進行振動監測時引入的高頻振動幅值。IMF2是頻率和振幅的關系，隨頻率的增加，振幅在逐漸增大，但將振幅值擴大時可以看出隨頻率增加振幅從變大到變小，中間會出現峰值振幅。IMF3又是速度隨時間的變化，將速度值變小時可以看到0.6 s左右時會有速度變化，將速度變大會看到速度為正弦波形變化。IMF4可以看出隨頻率的增加振幅逐漸趨于零。IMF5可以看出隨時間的增加速度在不斷變化。在上面的IMF信號分量中，IMF2～IMF5是進行研究的主要對象，在這其中含有信號的能量占有總能量中的絕大部分，屬于爆破振動信號中的優勢振動頻率。而最后一個分量IMF6則可能是儀器的飄零或信號本身最終的趨勢結果，沒有實際研究的價值和意義，可以忽略。因重構后的信號波形更符合爆破振動波的實際情況，將A和B的信號數據進行EMD重構，A和B的EMD重構信號如圖3和圖4所示。

圖3 A的EMD重構信號Fig.3 EMD reconstruction signal of A

圖4 B的EMD重構信號Fig.4 EMD reconstruction signal of B

從EMD重構信號中可以得出速度隨時間的變化規律，A的速度約為B的速度的兩倍，A在0.33 s左右時候速度達到最大0.035 cm/s，B在0.6 s時候速度達到最大0.070 cm/s。

2)邊際譜分析

對經過EMD重構后的A和B數據信號，再進行邊際譜分析。從數據信號的邊際譜中可以看出能量和頻率的相互關系，能量在頻率帶上的集中程度和爆破振動信號在不同頻率上的變化幅度[24]。A和B信號的邊際譜如圖5和圖6所示。

圖5 A的邊際譜Fig.5 Marginal spectrum of A

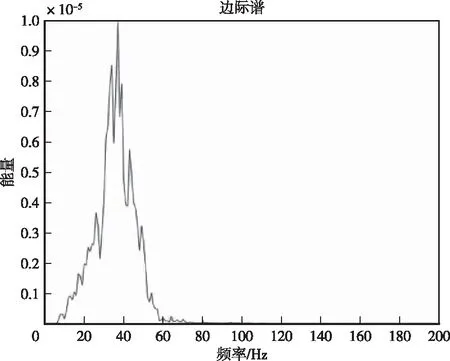
圖6 B的邊際譜Fig.6 Marginal spectrum of B

從圖5和圖6可以看出，信號A的主振頻率主要分布在0～100 Hz頻帶范圍內，最大能量約為3.3×10-6，80 Hz以下的低頻范圍內分布集中，包含多個頻帶，主振帶分別為30和40 Hz。截取的信號B的頻率主要分布在0～80 Hz頻帶范圍內，最大能量約為1.0×10-5，60 Hz以下的低頻范圍內分布集中，包含多個頻帶，主振帶分別為30和45 Hz。信號A和B的頻率主要分布區域相差不大，但是在峰值處的能量B約為A的三倍。

3)瞬時能量譜分析

邊際譜反映的是能量隨頻率的變化規律，但瞬時能量譜能夠直觀地看出瞬時能量隨時間的分布規律[25]。截取的A和B信號的瞬時能量譜如圖7和圖8所示。

圖7 A的瞬時能量譜Fig.7 Instantaneous energy spectrum of A

圖8 B的瞬時能量譜Fig.8 Instantaneous energy spectrum of B

從圖7和圖8中分析得出，信號A和B都是由導爆管起爆引起的結果，在圖中波形的峰值處表示瞬時能量的極值，A的波形范圍在0.1～0.5 s區域內，B的波形范圍在0.2～0.8 s區域內，即表示A和B的瞬時能量分別集中在0.1～0.5 s范圍內和0.2～0.8 s范圍內，A信號達到峰值瞬時能量在0.32 s左右，峰值瞬時能量約為1.38×10-3；B信號達到峰值瞬時能量在0.58 s左右，峰值瞬時能量約為5.00×10-3。從數據中可以看出，A信號的峰值瞬時能量約為B信號的峰值瞬時能量的3.6倍，從裝藥量入手，知A與B的單孔最大裝藥量一致，但測得的振動數據中，瞬時能量差異較大，從正交分析角度入手，說明爆破總用藥量也是影響最大瞬時能量的因素之一，振動信號的瞬時能量會隨著總裝藥量的增加而增大。瞬時能量代表著爆破的最大荷載，當瞬時能量過大，則爆破產生的爆破荷載也很大，一定強度范圍內的爆破振動，會讓爆破區周圍建(構)筑物的安全性及穩定性得不到保障，很容易超越建筑本身承受能力，會出現一定的損傷甚至倒塌、爆區地表邊坡的滑移及地下巷道冒落等各種損傷破壞問題。為了確保周圍建(構)筑物安全，控制爆破地震效應和改善巖石破碎效果，采取孔內間隔裝藥、控制炸藥單耗、降低總裝藥量、逐孔起爆、預裂爆破等技術以滿足降震要求和保證建構筑物的安全。使用高精度高強度數碼電子雷管起爆，精確控制延期時間，采用精確延時逐孔起爆的爆破技術手段，再結合上述的降振措施，在工人爆破技術都較高的操作水平下，爆破地震效應將會得到控制，巖石破碎效果將會得到改善，控制爆破技術又上一個新的水平。

4)三維譜分析

三維譜是基于三軸分析理論，用以研究爆破振動信號的一種波形分析理論，基于短時傅里葉變換形成的時間、頻率和瞬時能量三維譜圖，采用數字圖像處理的方法提取信號的特征，可以從空間直接反映能量隨時間和頻率變化的分布情況。以波形圖的顏色深淺作為判別的標準，顏色越鮮艷明亮，則代表能量越高，其爆破荷載也越大。在三維譜中，時間、頻率分別代表著X和Y軸，瞬時能量代表Z軸，三者相互作用，以空間立體圖反映了A的能量主要集中在0～0.8 s、0～50 Hz范圍內，B的能量主要集中在0～1.0 s、0～50 Hz范圍內，且可以通過顏色的深淺很好地觀察出來，以判別能量大小范圍。三維譜得到的數據結果與邊際譜和瞬時能量譜分析的結果相一致，說明此三者可以相互檢驗，互相驗證結果，以使得檢測分析更加精確。A和B信號的三維譜如圖9和圖10所示。

圖9 A的三維譜Fig.9 Three-dimensional spectrum of A

圖10 B的三維譜Fig.10 Three-dimensional spectrum of B

5)Hilbert能量譜

對IMF分量最后進行等高線能量圖分析，得到希爾伯特能量譜，該圖譜也基于顏色深度和集中度情況來區分，可以進行更加精確的時頻分析，同時以時間-頻率的方式展現振動信號原始的能量分布，避免了窗函數導致的能量損失以及小波基選取不合適而造成的干擾。信號A和B的等高線能量圖如圖11和圖12所示。

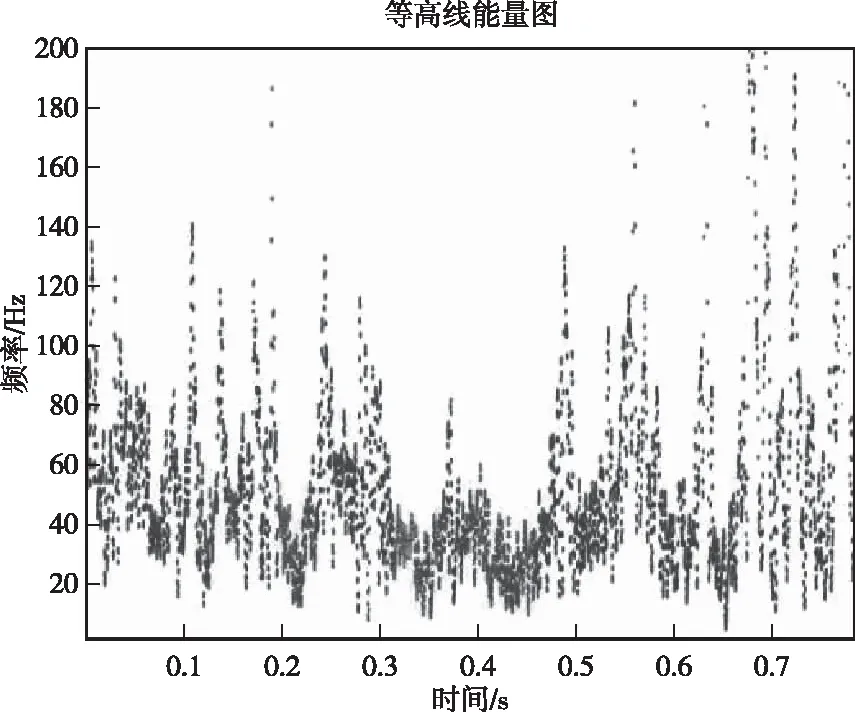
圖11 A的等高線能量圖Fig.11 Contour energy map of A

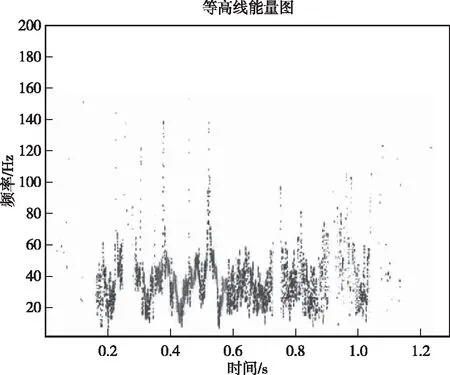
圖12 B的等高線能量圖Fig.12 Contour energy map of B

圖表明了不同IMF分量以頻率-時間-振幅的分布方式，可以看出，A振動能量主要分布在0～100 Hz以內，并且集中在50 Hz以下的低頻區域，其余少部分能量分布在100 Hz以上的頻段，B振動能量主要分布在0～60 Hz以內，并且集中在50 Hz以下的低頻區域，其余少部分能量分布在60 Hz以上的頻段，并且隨著質點振速的增加，爆破振動信號頻帶會朝低頻化發展。

3 結論

1)采用EMD-HHT分析法從爆破能量分布規律、爆破振動波形的頻譜特征、地震波衰減分析理論和爆破振動速度等方面進行研究分析。裝藥量的變化會影響振動頻率發生變化，藥量的增加會導致頻率從高頻往低頻發展，與此同時，最大爆破荷載也會隨著藥量的變化而變化。

2)在爆破振動波形圖中可以得到質點的峰值振速及主頻率等參量大小，兩者都是與爆破振動效應相關重要因素，峰值振速反映爆破荷載的大小，主頻率反映振動物的動態響應情況特征。基于上述物理量對爆破振動波形的研究分析得到的相關結論，可為今后的地下淺孔爆破提供更為精確的研究思路和方法。

3)基于邊際譜、瞬時能量譜和三維譜的研究分析，在考慮淺孔爆破振動對建構筑物安全性及穩定性影響的同時，應該重點考慮10～50 Hz低頻帶，淺孔爆破其主振頻率一般為40～100 Hz。