考慮儲存成本的集裝箱公鐵聯(lián)運路徑優(yōu)化*

徐 劍， 李周奇， 蔣 洋

(沈陽工業(yè)大學(xué) 管理學(xué)院， 沈陽 110870)

我國正逐漸步入“大交通”時代，單純的某種運輸方式已無法適應(yīng)時代需求，多種運輸方式聯(lián)合運輸越來越普遍且發(fā)展迅速。其中，公鐵聯(lián)運是適用范圍較為普遍的聯(lián)運方式，將公路的靈活性、簡捷方便、響應(yīng)時間短等優(yōu)點和鐵路運輸網(wǎng)絡(luò)四通八達、覆蓋面積大、穩(wěn)定性高、運量大等優(yōu)勢相結(jié)合，更好地實現(xiàn)了連續(xù)一體化運輸。集裝箱貨運是把貨物組合以集裝箱作為作業(yè)單元的一種運輸方式，其優(yōu)點是可以降低成本、提高作業(yè)效率，保障多式聯(lián)運的順利進行。目前集裝箱貨運進入了前所未有的發(fā)展與完善時期[1]。集裝箱公鐵聯(lián)運可將公路和鐵路貨物整體運輸有機組合，減少不必要的浪費、優(yōu)化作業(yè)流程、實現(xiàn)優(yōu)勢資源互補，使公鐵聯(lián)運效益最優(yōu)化[2]。

集裝箱公鐵聯(lián)運是內(nèi)陸集裝箱多式聯(lián)運的主要組成部分，不同的運輸路徑及運輸方式會產(chǎn)生不同的運輸效率和效益。為了達到提升集裝箱公鐵聯(lián)運體系效率和改善不合理運輸方式的目的，在高效協(xié)調(diào)公路、鐵路運輸銜接方式的前提下，應(yīng)進行合理的運輸組合模式選擇，使聯(lián)運經(jīng)營人得到最優(yōu)路徑，降低運輸總成本，從而獲取更高的收益。因此，加強對集裝箱公鐵聯(lián)運貨物運輸方式和運輸路徑的優(yōu)化，對提高聯(lián)運企業(yè)收益有重要的現(xiàn)實意義[3]。

在公鐵聯(lián)運中的關(guān)鍵問題之一就是聯(lián)運路徑的選擇(優(yōu)化)，即在不同因素、不同限制條件下模型的構(gòu)建和算法的改進。聯(lián)運路徑的優(yōu)化受運輸費用、運輸時間和環(huán)境等因素的影響[4]。在研究中，大多將運輸時間或運輸費用作為目標函數(shù)，如：Teng等基于國家綠色發(fā)展的背景，在運輸成本中考慮碳成本因素[5]；Yang等從多式聯(lián)運經(jīng)營者的角度出發(fā)，設(shè)計出雙重優(yōu)化目標模型，最大限度地減少了集裝箱多式聯(lián)運的總運輸成本和總運輸時間[6]。

一些學(xué)者考慮不同因素的約束建立模型，如：Ozdemir等提出了混合隱馬爾科夫模型(HMM)以解決運輸網(wǎng)絡(luò)中的路徑問題[7]；Chang考慮貨物交貨時間對運輸路徑的影響，建立了路徑優(yōu)化模型[8]；李珺等研究在不確定因素下建立混合不確定條件下的多式聯(lián)運路徑優(yōu)化模型[9]；于雪嶠等以客戶滿意度為約束，建立模糊需求的多式聯(lián)運路徑優(yōu)化模型[10]；劉暢等考慮貨物的時間成本價值建立多式聯(lián)運路徑選擇優(yōu)化模型，并用深度優(yōu)先搜索的算法對路徑選擇優(yōu)化模型進行求解[11]。

一些學(xué)者對路徑優(yōu)化的算法進行改進，如：熊桂武考慮模糊時間因素，建立了多式聯(lián)運路徑優(yōu)化模型，設(shè)計了混合田口遺傳算法求解算例[12]；Feng等通過蟻群算法解決聯(lián)運路徑選擇問題[13]；彭勇等以班期限制為切入點建立聯(lián)運路徑?jīng)Q策模型，同時改進遺傳算法對模型求解[14]；蔣洋等對運輸網(wǎng)絡(luò)優(yōu)化問題采用了啟發(fā)式算法[15]；成耀榮等設(shè)計變長符號編碼機制的文化基因算法，求解多式聯(lián)運路徑優(yōu)化問題[16]；程興群等考慮擁堵對運輸時間的影響，建立了多式聯(lián)運路徑選擇模型，并設(shè)計了基于保優(yōu)策略和移民策略的遺傳算法進行求解[17]；張小龍等改進基于Pareto適應(yīng)度的遺傳算法，并對多式聯(lián)運路徑優(yōu)化模型求解[18]。

通過對以上文獻的研究發(fā)現(xiàn)，雖然很多學(xué)者在建立模型時考慮了運輸成本和班期的限制，但他們大多忽略了在中轉(zhuǎn)節(jié)點等待時產(chǎn)生的儲存成本。在集裝箱公鐵聯(lián)運過程中，聯(lián)運經(jīng)營人只有在充分考慮各個方面影響的基礎(chǔ)上，才能選擇合理的運輸路徑和運輸方式，如忽略儲存成本和時間懲罰成本的影響，其結(jié)果可能在現(xiàn)實中無法實現(xiàn)。因此，本文以節(jié)點的儲存成本為切入點，在送達時間和班期限制的約束下充分考慮儲存成本和時間懲罰成本，建立運輸總成本最低的公鐵聯(lián)運路徑優(yōu)化模型，從而使模型更具有現(xiàn)實意義。

一、問題特征分析

考慮節(jié)點儲存成本的集裝箱公鐵聯(lián)運路徑優(yōu)化問題具有以下特征：

1. 多商品流路徑優(yōu)化

在集裝箱公鐵聯(lián)運網(wǎng)絡(luò)中，運輸任務(wù)表現(xiàn)為商品流。由于運輸企業(yè)同時承擔多個運輸任務(wù)，對不同客戶運輸任務(wù)不同，在實際運輸中往往存在多商品流。每個運輸任務(wù)都具有不同的運量、運輸期限、發(fā)貨點、收貨點、運輸起始時刻等。

2. 多約束的限制

隨著現(xiàn)代企業(yè)對庫存管理的要求不斷提高，客戶對不同貨物都有約定的到達時間，希望貨物能按照該時間準時到達。當貨物到達時間超出約定時間時，一方面會影響客戶對服務(wù)的滿意程度，另一方面也會影響運輸企業(yè)的口碑、信譽度等。同時，貨物到達時間也受班期限制的影響。本文設(shè)置各節(jié)點的軟時間窗限制，在軟時間窗限制、班期限制、不同商品流對到達時間限制的多約束限制下，進行集裝箱公鐵聯(lián)運路徑優(yōu)化問題研究。

3. 基于運輸總成本優(yōu)化模型

對于運輸企業(yè)而言，運輸總成本不僅是衡量企業(yè)運營狀況的一個重要指標，還是企業(yè)盈利的重要因素之一。在節(jié)點作業(yè)時，不僅存在換裝成本，還存在因等待最優(yōu)班列出發(fā)的等待成本。本文將節(jié)點的等待成本計入運輸總成本中，同時考慮節(jié)點間的運輸成本、節(jié)點內(nèi)的換裝成本和送達時超出時間限制的時間懲罰成本。

針對以上特征，在收貨時間限制、班期限制、不同商品流對到達時間限制的多約束限制下，建立由運輸成本、換裝成本、儲存成本和時間懲罰成本構(gòu)成的總成本最低的集裝箱公鐵聯(lián)運路徑優(yōu)化模型。

二、問題描述及假設(shè)

1. 問題描述

某運輸企業(yè)將多批不同數(shù)量的貨物從不同的運輸起點Oi(i=1，2，…，n)經(jīng)過支線運輸—干線運輸—支線運輸，將貨物運輸?shù)礁髯缘哪康牡谼i(i=1，2，…，s)，其網(wǎng)絡(luò)結(jié)構(gòu)如圖1所示。干線運輸包括樞紐節(jié)點間的運輸路徑及樞紐節(jié)點內(nèi)的運輸作業(yè)，存在公路、鐵路兩種運輸方式；支線運輸包括發(fā)貨點到樞紐節(jié)點和樞紐節(jié)點到收貨點的路徑及樞紐節(jié)點內(nèi)的運輸作業(yè)，只存在公路運輸方式。運輸時間由運輸距離和運輸方式?jīng)Q定。節(jié)點間不同運輸方式存在不同的運輸距離；若兩節(jié)點間某種運輸方式不存在，則假設(shè)兩節(jié)點間該種運輸方式對應(yīng)的運輸距離無限大。

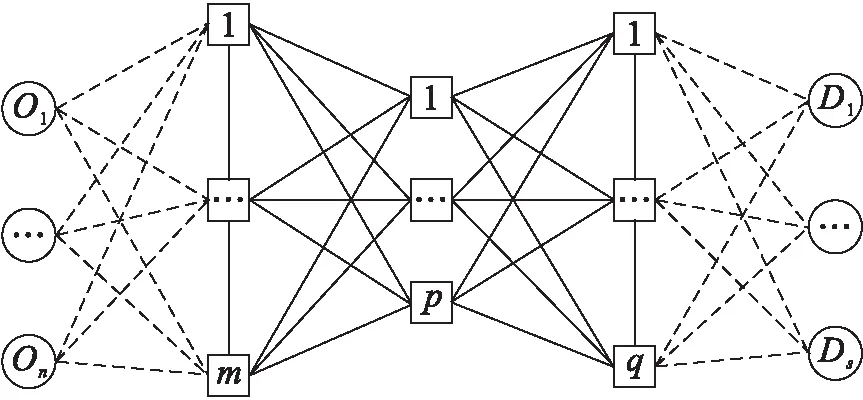
圖1 公鐵聯(lián)運網(wǎng)絡(luò)結(jié)構(gòu)

2. 研究假設(shè)

本文基于以下假設(shè)：(1)運輸任務(wù)的起訖點已知；(2)在一個運輸任務(wù)內(nèi)，兩節(jié)點間進行運輸時只能選擇一種運輸方式，轉(zhuǎn)運只能發(fā)生在節(jié)點處，且運量不可分割；(3)同一任務(wù)在相同節(jié)點最多只能中轉(zhuǎn)一次；(4)每條運輸路徑都有足夠的能力進行運輸；(5)每個中轉(zhuǎn)節(jié)點都具有足夠的能力實現(xiàn)貨物中轉(zhuǎn)運輸；(6)火車有規(guī)定的出發(fā)時間，汽車可以隨時出發(fā)。

三、模型構(gòu)建

1. 模型參數(shù)及決策變量說明

模型中各參數(shù)含義如表1所示。各決策變量含義如表2所示。

表1 模型參數(shù)說明

表2 決策變量說明

2. 目標函數(shù)設(shè)計

本文研究的集裝箱公鐵聯(lián)運路徑優(yōu)化問題，以運輸總成本最低為優(yōu)化目標。該運輸總成本包括運輸成本、換裝成本、儲存成本和超出最晚時間到達終點的時間懲罰成本。運輸成本產(chǎn)生于不同節(jié)點采用不同運輸方式進行運輸?shù)倪^程中；換裝成本主要產(chǎn)生于各節(jié)點的換裝作業(yè)中；儲存成本產(chǎn)生于早到節(jié)點后等待最優(yōu)班列的等待時間中；時間懲罰成本產(chǎn)生于貨物超出最晚時間送達收貨點時，和總的運輸時間有重要關(guān)聯(lián)。

(1) 運輸成本C1。運輸成本包括集裝箱公鐵聯(lián)運網(wǎng)絡(luò)中各種運輸方式在運輸路徑中產(chǎn)生的成本，主要與運輸方式的運價、運量和運輸距離有關(guān)，計算公式為

(1)

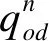
(2) 換裝成本C2。在公鐵聯(lián)運網(wǎng)絡(luò)中，由于運輸方式和運輸班列的改變都會產(chǎn)生換裝成本，計算公式為

(2)

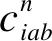
(3) 儲存成本C3。在公鐵聯(lián)運網(wǎng)絡(luò)中貨物中轉(zhuǎn)時，由于火車有班期限制，早到節(jié)點會產(chǎn)生一定的等待時間，在這期間內(nèi)會產(chǎn)生儲存成本C3，其表達式為

(3)

(4)

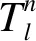
3. 約束條件分析

研究商品流公鐵聯(lián)運路徑優(yōu)化問題，既要保證每個OD流的平衡，又需考慮運輸方式的連貫性。為實現(xiàn)對模型約束的全面刻畫，建立搭乘最優(yōu)班列約束、商品流約束、運輸方式轉(zhuǎn)換約束、中轉(zhuǎn)次數(shù)約束、送達時間約束，即

(5)

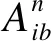
(6)

(7)

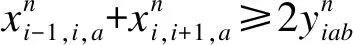
(8)

(9)

式(6)、(7)共同限定每個運輸任務(wù)只能對應(yīng)一個起點和一個終點，保證貨流不可拆分原則；式(8)保證運輸方式轉(zhuǎn)換順利進行；式(9)保證每個運輸任務(wù)中相鄰節(jié)點只能選擇一種運輸方式進行運輸。將式(6)～(9)相結(jié)合，確保了聯(lián)運網(wǎng)絡(luò)中各商品流通起訖點之間運輸路徑的唯一性和完整性，即

(10)

式(10)為節(jié)點中轉(zhuǎn)約束，保證每個運輸任務(wù)只能在節(jié)點i進行中轉(zhuǎn)，且中轉(zhuǎn)次數(shù)不超過1次，以確保運輸?shù)暮侠硇浴?/p>

(11)

式(11)保證每個運輸任務(wù)在運輸最晚時間前完成運輸。

(12)

4. 模型表達

結(jié)合對目標函數(shù)及約束條件的分析，構(gòu)建復(fù)雜約束下集裝箱公鐵聯(lián)運路徑優(yōu)化模型，即

(13)

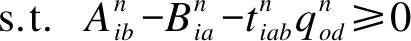
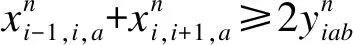
四、算例分析

現(xiàn)假設(shè)聯(lián)運企業(yè)在零點時承擔2份運輸任務(wù)，以常州和無錫為起點，經(jīng)南京、上海、鄭州等8個樞紐節(jié)點運輸?shù)疥柸托吓_，其網(wǎng)絡(luò)結(jié)構(gòu)及節(jié)點編號如圖2所示。

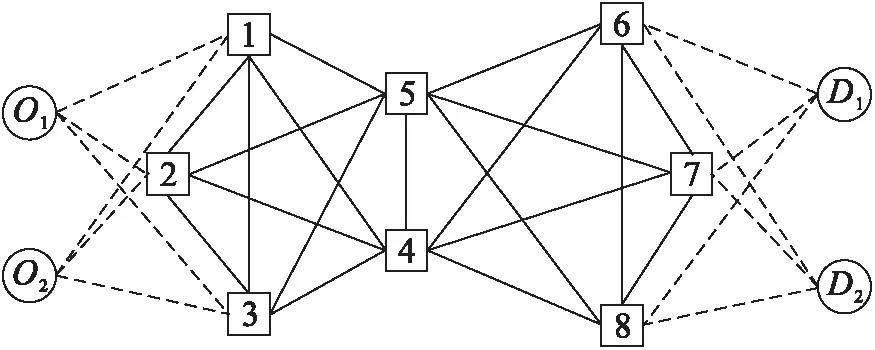
圖2 公鐵聯(lián)運運輸網(wǎng)絡(luò)示意

要求找到運輸路徑和運輸方式的組合使運輸總成本達到最低，同時滿足發(fā)貨人運輸時間的要求。運輸任務(wù)見表3，各節(jié)點的換裝具體信息和路徑信息均已知。

表3 運輸任務(wù)信息

根據(jù)以上信息，運用MATLAB對集裝箱公鐵聯(lián)運路徑優(yōu)化模型求解。運輸方式中1代表公路、2代表鐵路，v1=80 km/h、v2=70 km/h；參數(shù)設(shè)計為種群規(guī)模N=80，交叉概率Pc=0.9，變異概率Pm=0.01，連續(xù)迭代100次終止運算。據(jù)此得到圖3算法收斂軌跡和圖4最優(yōu)路徑結(jié)果。

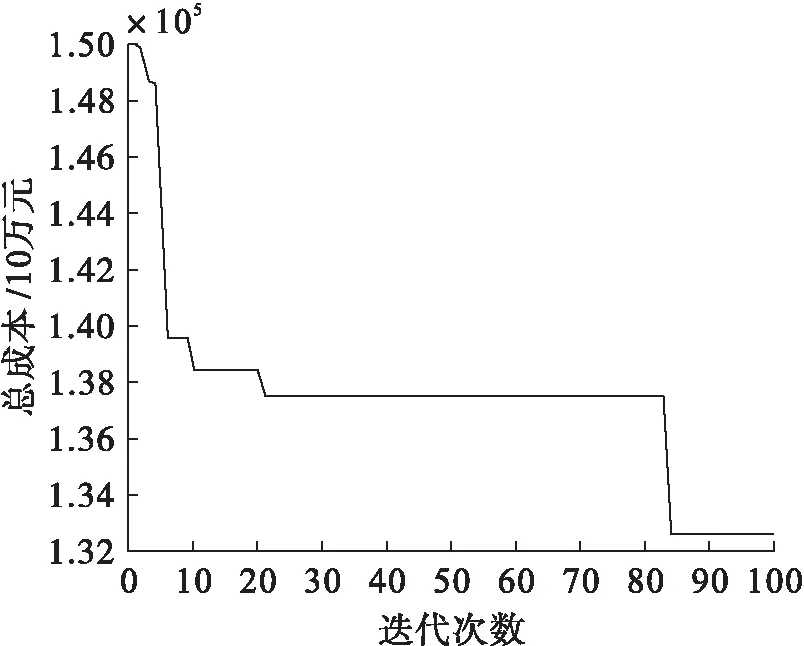
圖3 算法收斂軌跡

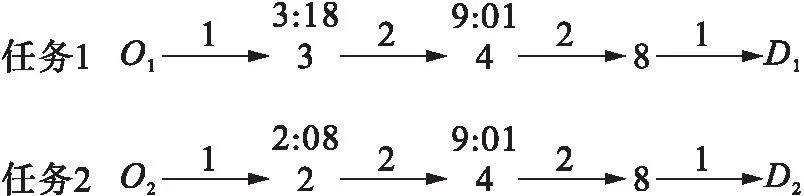
圖4 最優(yōu)路徑結(jié)果

任務(wù)1從O1到達樞紐節(jié)點3，搭乘3∶18的火車到達樞紐節(jié)點4，經(jīng)過轉(zhuǎn)裝等待搭乘9∶01的火車到達樞紐節(jié)點8，最終經(jīng)公路運輸?shù)绞肇淈cD1；任務(wù)2從O2到達樞紐節(jié)點2，搭乘2∶08的火車運輸?shù)綐屑~節(jié)點4，搭乘9∶01的火車到達樞紐節(jié)點8，最后由公路運輸?shù)竭_最終收貨點D2。目標函數(shù)值為132 691元，其中任務(wù)1為54 507元、任務(wù)2為78 184元。

五、結(jié) 語

本文在“大交通”的時代背景下研究集裝箱公鐵聯(lián)運路徑優(yōu)化問題，以節(jié)點間運輸成本、節(jié)點換裝及儲存成本、超出最晚時間的懲罰成本構(gòu)成的總運輸費用為目標函數(shù)，考慮班期限制、收貨時間限制建立集裝箱公鐵聯(lián)運路徑優(yōu)化模型。通過算例將兩個運輸任務(wù)經(jīng)南京、鄭州等節(jié)點送到收貨地，并用MATLAB軟件求解得出最終的運輸路徑，證明了模型的有效性。