巖心體積節理數JV′計算方法

王 燕 陸詩磊

(常州市建筑科學研究院集團股份有限公司，江蘇 常州 213015)

1 概述

巖體中往往存在多組結構面，這些結構面又稱節理，是反映巖石完整度的重要指標[1]。GB/T 50218—2014工程巖體分級標準第3.3.2～3.3.4規定巖體完整程度的定量指標，應采用巖體完整性指數KV，KV應采用實測值。當無條件取得實測值時，也可用巖體體積節理數JV[2]。巖體體積節理數JV、巖體完整性指數KV以及巖體完整程度的對應關系，如表1所示。

表1 JV與KV及巖體完整程度的對應關系

同時該規范第B.0.2條規定了巖體體積節理數可采用間距法進行計算，其計算公式如式(1)所示。

(1)

其中，JV為巖體體積節理數，條/m3；n為統計區域內結構面組數；Si為第i組結構面沿法向每米長結構面的條數；S0為每立方米巖體非成組節理條數。

通過間距法對巖體體積節理數的計算應符合下列規定：

1)測線應水平布置，測線長度不宜小于5 m；根據具體情況，可增加垂直測線，垂直測線長度不宜小于2 m。

2)應對與測線相交的各結構面跡線交點位置及相應結構面產狀進行編錄，并根據產狀分布情況對結構面進行分組。

3)應對測線上同組結構面沿測線方向間距進行測量與統計，獲得沿測線方向視間距。應根據結構面產狀與測線方位，計算該組結構面沿法線方向的真間距，其算數平均值的倒數記為該組結構面沿法向每米長結構面的條數。

4)對跡線長度大于1 m的分散節理應予以統計，已為硅質、鐵質、鈣質膠結的節理不應參與統計。

2 巖心體積節理數JV′的計算方法

通過對上述間距法進行分析，根據曾聯波學者2008年對結構面、節理以及裂縫的解釋及描述[3]，Si為第i組結構面沿法向每米長結構面的條數，即第i組結構面的線密度Ri′，而S0為每立方米巖體非成組節理條數，即非成組結構面的體密度R0[3]。因為視間距已經過產狀校正為真間距，結構面產狀平行于巖體底面，故結構面線密度與該巖體的底面積數值無關，假定該段巖體的底面積為1 m2，則第i組結構面的線密度Ri′即為該段巖體第i組結構面的體密度Ri。故巖體體積節理數JV亦可用式(2)表征：

(2)

其中，JV為巖體體積節理數，條/m3；n為統計區域內結構面組數；Ri為第i組結構面的體密度；R0為非成組結構面的體密度。

不難得出，當巖體結構面分布均勻時，沿結構面法線方向在巖體中取出多節巖心，通過式(2)分別計算出它們的巖心體積節理數JV′，這些巖心體積節理數的平均值與利用式(1)計算出的該巖體的巖體體積節理數JV′，其數值是相同的。

而經過對巖體體積節理數JV的重新表征，引入結構面線密度、體密度的概念，則利用間距法測試JV可不再受巖體體積大小及測線長度的約束。

對于地下埋藏較深的巖體，受鉆探技術的影響，我們并不能取出足夠大的巖體并利用式(1)對其進行間距法測試巖體體積節理數從而評估其完整性(通常取出的巖心直徑僅有89 mm～137 mm)。而根據本文我們可以利用式(2)來對巖心體積節理數JV′進行定量計算。

計算時需注意非成組結構面體密度R0應通過式(3)求取：

R0=Ti÷Vi

(3)

其中，R0為非成組結構面的體密度；Ti為測試巖心中非成組結構面的條數；Vi為測試巖心的體積。

而第i組結構面的體密度Ri亦可用線密度Ri′表征，但是兩者并不是等價關系，由于對視間距校正為真間距，其底面也由視底面校正為真底面，其產狀與水平面的夾角即為結構面的傾角，則Ri必須由Ri′進行鉆遇率修正，如式(4)所示。

Ri=Ri′ ×cosθ

(4)

其中，Ri為第i組結構面的體密度；Ri′為第i組結構面的線密度；θ為結構面的傾角。

其中鉆遇率即鉆探過程中遇到該組結構面的概率，其示意圖如圖1所示。

3 工程實例驗證

在實際工程實施過程中，對某市某鎮某地塊三疊灰巖分別通過巖心體積節理數及巖體完整性指數來評價其完整程度，其結果是一致的。因此通過巖心體積節理數來判別地下埋藏巖體的完整程度是可行的。具體驗證情況如下：

根據某市某鎮某地塊取出的三疊灰巖巖心(所取孔號在場地均勻分布具有代表性)，通過其結構面進行分組描述，并剔除充填的結構面，利用式(1)～式(3)進行巖心體積節理數JV′計算，并根據各巖心體積進行加權求平均值，算出該場地三疊紀灰巖的巖體體積節理數JV，從而判別其完整程度。具體結果如表2所示。

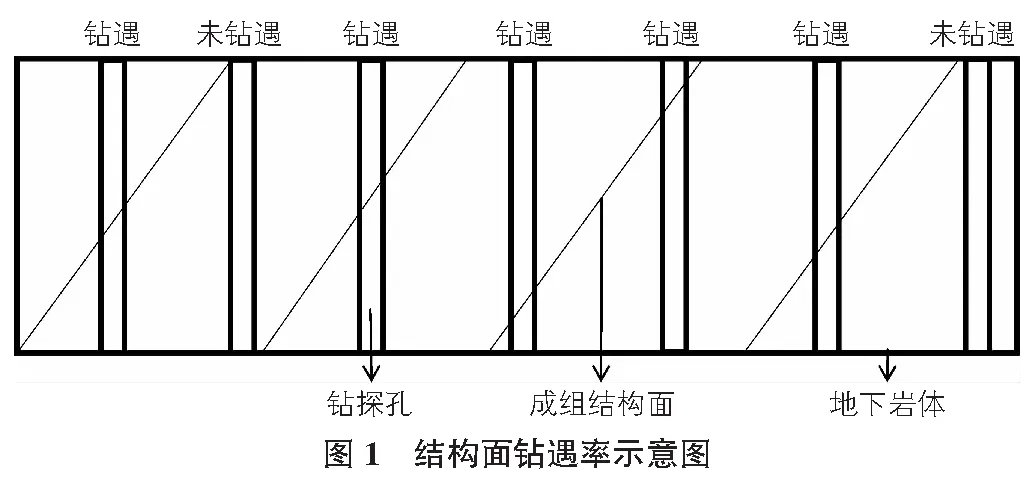
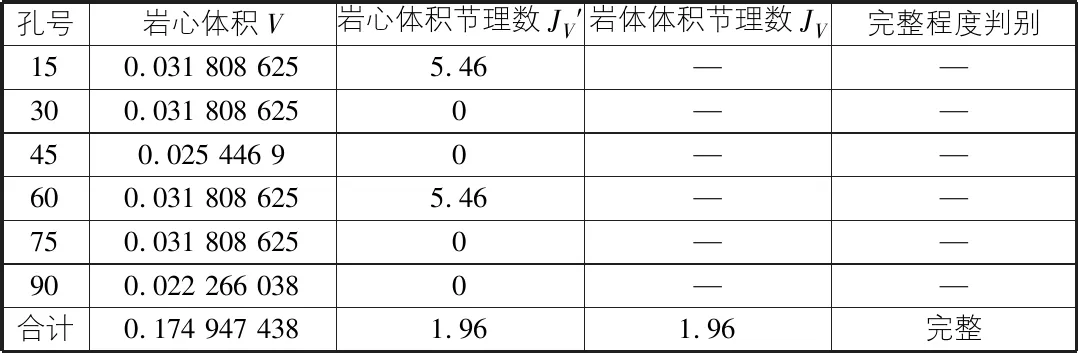
表2 利用巖心體積節理數JV′判別宜興丁蜀三疊紀灰巖完整程度表

通過對該地區巖體和巖心進行波速測試，得出巖體完整性指數KV的值為0.91，判斷巖體完整性指數為完整。與巖心體積節理數判別結果一致。

4 結語

本文通過引入結構面體密度與線密度的概念，將間距法測試巖體體積節理數JV的公式加以改進拓展，使其不受巖體體積大小及測線長度的限制，從而使間距法適用于巖心體積節理數JV′的求取，并通過對第i組結構面的體密度Ri進行鉆遇率修正，對非成組結構面的體密度R0進行巖心體積修正，最終得到利用間距法求取巖心體積節理數JV′的計算公式，對埋藏地下的巖體完整程度的定量表征具有重要意義。