壓力容器聲發射定位算法研究

孫瓊瓊，車 剛，田 裕

(泰安市特種設備檢驗研究院，山東 泰安 271000)

1 前 言

隨著工業的發展，壓力容器作為重要的承壓類特種設備，在各工業系統中發揮著至關重要的作用，同時壓力容器也是一種危害性極大的特種設備，當其發生故障時會引起爆炸、中毒等事故，不僅對周圍環境及人身安全造成重大威脅，甚至造成國民經濟的重大損失[1]。因此定期對壓力容器監測、檢驗，能對可能發生的缺陷、故障進行預報，從而可以保障壓力容器的安全運行。

外力作用下，壓力容器材料產生變形、斷裂并以瞬態彈性波形式釋放應變能的現象稱為聲發射(Acoustic Emission，AE)[2]。聲發射是一種可靠的無損檢測技術，在檢測領域得到了廣泛應用。通過對壓力容器進行聲發射檢測，并進行聲源定位，可精確定位缺陷位置，減少盲目檢測，及時排除安全隱患，降低惡性事故發生的幾率，實現企業經濟效益最大化。

2 最小二乘法定位算法

圖1 空間坐標系Fig.1 Spatial coordinate system

(1)

式中，x，y，z，t為未知數，v代表波速，ti代表聲源到達傳感器的時間，t代表金屬斷裂的時間。理論上可以選用4個傳感器建立方程，從而求得聲源位置及金屬斷裂時間。但當傳感器大于4個時，可以減少誤差，使得聲源坐標更加準確。若將非線性方程線性化，利用最小二乘法則可以迅速求得聲源位置[3]。由(1)式可得：

(x-xi)2+(y-yi)2+(z-zi)2=v2(ti-t)2

(2)

選用5個傳感器，即i=1,2,3,4,5，建立方程組。各項對第一項求差，求得方程

akx+bky+ckz+dkt=ek

(3)

式中，k=1, 2, 3, 4, 5，ak,bk,ck,dk,ek為求差后各項系數，將(3)式寫成AX=B，利用最小二乘法求解：x*=(ATA)-1ATB，從而求得聲發射源位置。

3 Geiger定位算法

Geiger算法定位原理是通過給定一個初始值多次迭代逐漸逼近聲源實際位置[4]。每次迭代都是計算一個新的修正向量Δθ=(Δx, Δy, Δz, Δt)T，將修正向量加到上次迭代的結果上，得到一個新的試驗點，判斷這個試驗點是否滿足要求，如果滿足要求，此坐標點即為所求聲發射源位置，如果不滿足則繼續迭代。利用式(4)作為迭代方程，進行定位求解。

(4)

式中，(x,y,z)為聲源坐標，t為聲發射時間，(xi,yi,zi)為第i個傳感器的位置，ti為聲源信號到達第i個傳感器的時間，v代表波速。

對于聲發射信號到達每個傳感器的時間t0i，其一階泰勒展開式表示為：

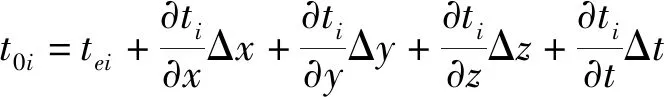
(5)

對于N個傳感器，可利用AΔθ=B表示。其中：

(6)

由最小二乘法計算，可得

ATAΔθ=ATB

(7)

(8)

由方程(8)求出修正向量后，以θ+Δθ為新的試驗點繼續迭代，直到滿足誤差要求。初始值可選擇幾個傳感器包圍范圍的中心點坐標，時間為傳感器接收到信號時間的平均值。

4 基于最小二乘法的Geiger優化迭代組合定位算法

基于最小二乘法的Geiger優化迭代組合定位算法是將最小二乘法計算得到的坐標點作為Geiger算法的初始迭代點。兩個算法的結合，省去了尋找最優步長因子的大量計算時間，提高算法的求解速度，同時縮短了求解時間。

建立如式(4)的數學模型，未知數為：x,y,z,t,v，所以至少需要5個傳感器接收聲發射信號，進行定位求解。當有5個以上的傳感器接收到聲發射信號時，就可建立一個方程組用最小二乘法對方程組求解，得到聲發射定位迭代算法初始迭代點，然后利用Geiger算法進行多次迭代運算即可實現定位。

5 結 語

本文針對壓力容器檢驗現場的聲發射信號的定位問題，研究了最小二乘法的估計特性以及Geiger定位算法的優化迭代，最終利用基于最小二乘法的Geiger優化迭代組合定位算法進行聲源定位，能有效的提高運算速度，節省運算時間，可廣泛應用于工程實踐。