基于光照度的農田蒸散量估算方法研究

蘇寶峰 張旭東 米志文 杜鶴娟

(1.西北農林科技大學機械與電子工程學院， 陜西楊凌 712100； 2.農業農村部農業物聯網重點實驗室， 陜西楊凌 712100；3.西藏民族大學信息工程學院， 咸陽 712089)

0 引言

蒸散量(ET)的精確估算對了解作物需水、指導灌溉起到關鍵作用，對揭示區域性農業氣候特征和生態環境差異也具有重要作用[1-7]。

目前，在蒸散量估算研究中，既要降低對輻射數據的依賴，又要提高蒸散量的估算精度[8-12]。例如基于溫度的哈格里夫斯(Hargreaves-Samani, H-S)模型，其主要數據為空氣溫度，但在實際應用中常需地域校準或引進輻射數據[13-14]。賈悅等[15]將輻射因子引入H-S模型中，提高了模型的穩定性。ZAHRA等[16]將基于溫度法的簡化模型和基于輻射法的簡化模型進行對比，解釋了不同類型模型的適應性問題。然而，測量太陽輻射的輻射計成本很高[17-18]，全球的輻射監測站點遠少于氣象監測站點[19-23],無法在農業實際應用中大范圍安裝和布署。

光照度反映太陽輻射中可見光波段的光強度，光照度傳感器用于測量光照的明暗程度，雖然無法直接測量不可見光波段的光強度，但在太陽輻射的全波段中可見光與不可見光波段的能量比例較穩定，因此通過光照度表述太陽的輻射作用，從而進行蒸散量的估算尚有待探索。

機器學習回歸算法是影響蒸散量估算精度的一個重要因素。現階段，多采用單元機器學習回歸算法[24-26]。馮禹等[27]構建了基于遺傳算法優化的誤差反向傳播神經網絡(Back propagation neural network,BPNN)蒸散量預測模型，改善了局部最優解現象，但尚未表明單一模型的穩定性。HOSSEIN等[28]利用自適應神經模糊系統(Adaptive network-based fuzzy inference system,ANFIS)精準擬合非線性關系的特性，將其用于ET與氣象數據的非線性擬合，其模擬精度高于常規的公式法。WALLS等[29]以波文比儀器的觀測值作為數據源，采用人工神經網絡(Artificial neural network, ANN)預測蒸散量，有效地預測了逐時級的蒸散量。

集成算法可解決單元機器學習模型性能精度低、泛化性能差的問題。SUN等[30]采用融合了BPNN、廣義回歸神經網絡(Generalized regression neural network,GRNN)、極限學習機(Extreme learning machine,ELM)和SVR的集成學習算法，進行PM2.5逐時預測，提高了模型的預測精度。集成算法在短期光伏發電預測、生物質熱解等領域也表現出穩定、高效的模型性能[31-32]。因此，有必要研究集成學習算法在蒸散量估算中的適用性。

本文將渦度相關系統觀測的實際蒸散量作為被預測量，采用光照度代替太陽輻射，提出晴朗指數，構建融合極端梯度提升模型(XGBoost)、分布式梯度提升框架(LightGBM)、支持向量回歸(SVR)、隨機森林回歸(RFR)的多元集成實際蒸散量(ETa)估算模型，并與XGBoost、LightGBM、SVM、RFR算法進行比較，為簡化蒸散量估算以及在農業實際中應用和推廣蒸散量提供科學依據。

1 材料和方法

1.1 試驗區概況

試驗區位于陜西省中國旱區節水農業研究院的玉米種植試驗田(34°17′58.47″N，108°4′2.93″E，海拔525 m)，年均蒸發量1 500 mm。試驗期間田間種植夏玉米，試驗區地形開闊，附近多為農田，渦度相關系統位于農田中央。

1.2 數據獲取和處理

1.2.1氣象數據和蒸散量數據獲取

在夏玉米輪作旱田安裝渦度相關系統(Open path eddy covariance，OPEC)。圖1為渦度相關系統和光照度記錄儀。該系統主要組成部分為：CAST3A型三維超聲風速儀、LI75600A型開路CO2/H2O分析儀、CR1000型數據采集器、HMP-60型空氣溫濕度探頭、LI200SZ型輻射量表和HFP01SC型熱通量板等[8]。

渦度相關系統獲取空氣溫度、空氣濕度、凈輻射和實際蒸散量數據；光照度記錄儀安裝在固定輻射傳感器的橫臂上，型號為MAX44009，量程為0～200 000 lx，用于記錄與渦度相關系統對應采集時間的光照度。兩個設備的數據同時采集和記錄，數據每30 min同步記錄1次。記錄2019年6月22日—9月22日共計3 648組數據。

1.2.2晴朗指數

在蒸散量數據集中提出晴朗指數描述不同天氣類型下逐時蒸散量分布特征。影響蒸散量的主要氣象因子有太陽輻射和空氣溫度[33]。目前蒸散量的估算研究直接用氣象數據作為數據源，在進行蒸散量逐時估算研究中，作為同一天的氣象數據時存在當日太陽輻射分布差異較大導致蒸散量的分布差異較大。不同天氣類型條件下蒸散量的變化趨勢具有很明顯的特征差異。而模型的輸入特征中并無對天氣類型的描述，減弱了模型的估算效果。為此提出基于光照度數據的晴朗指數。將每日的光照度均值作為當日的晴朗指數，其計算公式為

式中n——當日光照度數據點個數

S——晴朗指數

Xi——第i個數據點光照度，lx

1.3 蒸散量估算算法

在蒸散量的估算研究中，核心問題在于準確描述氣象因子與蒸散量之間的非線性關系。集成算法是最近發展起來的，可解決單元模型性能精度低、穩定性差的問題。然而，蒸散量估算多通過XGBoost、LightGBM、SVM回歸、RFR回歸等單元回歸算法實現，還未采用多種單元模型組合的集成算法。為此本研究基于以上4種單元模型構建集成學習算法，探索集成算法在蒸散量估算問題中的模型性能。

1.3.1單元模型

XGBoost是一種梯度增強回歸樹的改進算法。與LightGBM算法相比，XGBoost采用Pre-sorting算法[34]，能夠根據數據特征準確找到分裂點，提高模型的精度，在數據挖掘比賽中使用廣泛。LightGBM算法是一種新的梯度提升框架。對比XGBoost算法，LightGBM采用Leaf-Wise生長策略，提高了模型的訓練效率，同時，增加了最大深度限制，在保證高效率的同時防止過擬合問題的出現。RFR是決策樹算法之一，主要用來解決回歸問題，RFR在決策樹的訓練過程中引入了隨機數據選取和隨機特征選擇，使得模型更具有魯棒性。SVR是支持向量機(Support vector machine,SVM)中的一個重要的應用分支。其通過引入懲罰因子提高了模型的泛化性能。同時，引入的多種核函數可以靈活地解決各種非線性回歸問題。

1.3.2集成算法

集成算法是目前機器學習領域研究中的熱門方向。集成學習通過組合多種弱學習器得到一個預測效果比較好的強學習器。在數據不充分時，集成學習采用bootstrap進行數據抽樣，得到多個數據集，分別進行訓練后再組合。在弱學習器的選擇中集成學習遵循“好而不同”的原則，即弱學習器間擁有各自的優點。如圖2所示，集成算法的主要思想是訓練模型來學習使用底層學習器的預測結果，其中基礎學習器在所有數據集上生成預測結果，次學習器會基于基礎學習器的預測結果進行再訓練進而提高模型的精度。

蒸散量估算的集成算法的訓練過程如下：首先在數據處理階段將空氣溫度、空氣濕度、飽和水汽壓差和光照度作為特征向量，實測蒸散量作為目標量建立訓練集和測試集。如圖3所示，訓練集經過三折交叉驗證產生3組訓練樣本集，分別將其中的2組用于基礎學習器訓練，1組作為驗證集進行預測。這樣對于每一個基礎學習器均可得到3組預測結果和3個模型，將3組預測結果進行合并記為A1。同時，將測試集分別代入3個模型進行預測，將3組預測結果進行加權平均和整合記為B1。對于XGBoost、LightGBM、RFR以及SVR 4種基礎學習器會產生對應的A1、A2、A3、A4和B1、B2、B3、B4 4對數據集。其中，A1～A4分別包含了4個基礎學習器的模型特征，將A1～A4合并作為次學習器的訓練集，B1～B4合并作為次學習器的測試集。次學習器將每個基礎學習器的預測結果作為特征進行學習訓練，即給基礎學習器的預測結果賦予權重，來使最后的蒸散量估算更為準確。

1.3.3模型的超參數尋優算法

在通過機器學習算法建立氣象因子與蒸散量的非線性關系中，模型超參數的最優選擇直接決定了算法的性能。隨機搜索和網格搜索是常用的兩種超參數優化方法。隨機搜索能快速地縮小超參數的范圍，而網格搜索較隨機搜索能更精確確定超參數的數值。本研究中，首先采用隨機搜索快速確定超參數的大致范圍，再通過網格尋優精確確定超參數的最優組合。同時通過交叉驗證提高模型的泛化性能。XGBoost、LightGBM、SVR、RFR 4種模型的主要超參數如表1所示。

表1 單元模型超參數Tab.1 Element model hyperparameters

1.4 精度驗證

通過均方根誤差(RMSE)和決定系數(R2)驗證數據的可靠性，分別分析不同蒸散量模型和晴朗指數校正的結果。RMSE越小，R2越接近1，說明模型的精度越高，預測性能好。

2 結果與分析

渦度相關系統記錄的原始通量數據經過Eddypro軟件處理，得到實際蒸散量數據作為數據集的被預測量。渦度相關系統采集的空氣溫度、空氣濕度、太陽輻射以及光照度記錄儀采集的光照度數據和引入的晴朗指數作為預測量。其中，太陽輻射和光照度用來描述太陽光照強弱，作為預測量輸入XGBoost、LightGBM、RFR、SVR 4種單元模型和集成模型，用于驗證光照度代替太陽輻射估算蒸散量的可行性。本文首先通過相關性分析以及回歸建模驗證光照度代替太陽輻射的可行性，其次基于光照度采用集成算法建立實際蒸散量估算模型，最后，在基于光照度的氣象數據中引入晴朗指數，分析晴朗指數在蒸散估算中的作用。

2.1 光照度與太陽輻射相關性分析

在進行光照度與太陽輻射以及空氣溫度與太陽輻射的相關性分析中，同時采用Pearson相關系數和Spearman相關系數。Pearson相關系數受限于數據的分布情況，而Spearman相關系數是一種與分布無關的檢驗方法。同時采用以上兩種檢驗方法更能反映實際的相關情況。光照度與太陽輻射在Pearson和Spearman相關性分析中，相關系數分別為0.967 7、0.891 4，表明光照度與太陽輻射的相關性極高。空氣溫度與太陽輻射的相關性較低，但也有一定的相關性特征，相關系數分別為0.627 1、0.579 6。以上分析表明了通過光照度、空氣溫度代替太陽輻射的可行性。采用了線性回歸、回歸樹、支持向量機以及高斯回歸建立光照度預測太陽凈輻射的模型，結果如表2所示，通過4種回歸算法建立光照度、空氣溫度與太陽輻射回歸模型的R2均為0.94，初步驗證了通過機器學習算法太陽輻射可被光照度替代。

表2 太陽輻射回歸模型Tab.2 Solar radiation regression model

2.2 基于光照度的蒸散量估算

首先，建立空氣溫度、空氣濕度、飽和水汽壓差、光照度與蒸散量之間的非線性關系。隨機選取數據集中的80%作為訓練集，20%作為測試集。通過網格搜索和隨機搜索組合的超參數尋優方法，確定各個單元模型的超參數。訓練集共2 918組，測試集共730組，驗證不同模型的預測能力。用測試集分別驗證XGBoost、LightGBM、RFR、SVR 4種單元模型的預測性能，將4個單元模型的預測結果作為集成模型的輸入特征向量進行回歸，建立基于光照度的蒸散量估算模型。

圖4為基于光照度的4種單元模型和集成模型的蒸散量估算結果，XGBoost、LightGBM、RFR、集成模型的R2在0.9以上，其中集成模型的擬合效果最好，R2為0.955，集成模型的RMSE最小，為0.065 mm/h。表明光照度在蒸散量預測中效果良好，也初步表明集成算法的性能優于4種單元模型。

由圖5可知，通過空氣溫度、空氣濕度、飽和水汽壓差和太陽輻射作為輸入預測蒸散量，LightGBM、集成模型R2在0.9以上，最優R2為0.905，RMSE最小為0.094 mm/h。表明太陽輻射在蒸散量預測中同樣具有良好的預測效果。

表3為分別通過光照度和太陽輻射估算蒸散量的模型結果對比，模型精度差異較小，R2最大差值為0.053，RMSE最大差值為0.031 mm/h，尤其是在SVR模型中，RMSE與R2的差異最小。太陽輻射和光照度預測蒸散量的性能很接近，證明了光照度替代太陽輻射作為預測蒸散量的輻射類數據的可靠性。其次，從訓練算法角度進行分析評價，集成模型的整體性能優于單元模型。從基于光照度的蒸散量模型對比中可以發現，集成模型的R2與RMSE均優于單元模型。同樣，基于太陽輻射的蒸散量模型中也能得出相同的結論。表明集成模型在解決蒸散量非線性問題時具有優勢。

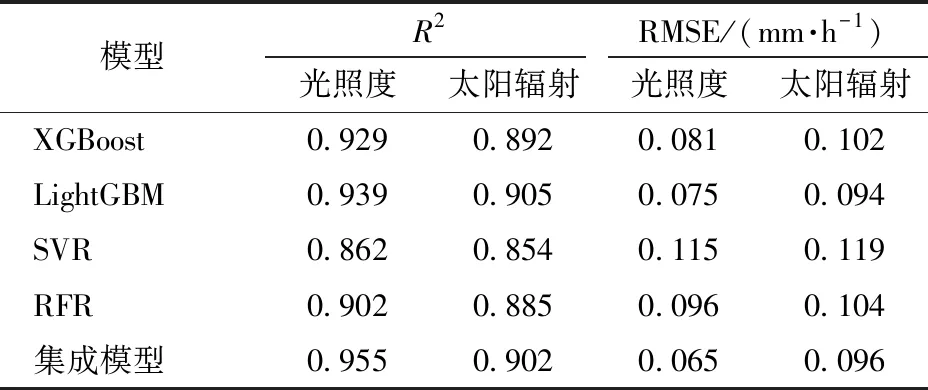
表3 光照度與太陽輻射估算蒸散量模型比較Tab.3 Comparison of illuminance and solar radiation estimation evapotranspiration models

2.3 晴朗指數對蒸散量估算精度的影響

不同天氣條件下蒸散量的變化趨勢具有很明顯的差異。如圖6所示，為了更加直觀說明天氣類型和蒸散量間的關系，將每日的逐時級實際蒸散量和光照度數據進行對比分析。以7月1日的蒸散量分布和光照度分布為例，7月1日的光照度分布與前一天差異較大時，其蒸散量分布也存在較大差異。這說明了在進行當日逐時級實際蒸散量估算中，當日的光照度分布情況對逐時級的蒸散量有較大影響。同理，在數據集中的其他日期也基本符合上述特征，而在2.2節部分模型的輸入特征數據中并無對光照度分布的描述，降低了模型的預測效果。為此，在蒸散量的預測數據集中引入晴朗指數，作為逐時級蒸散量估算的懲罰因子。

在引入晴朗指數后，4種單元模型和集成模型的訓練結果如圖7所示。5種模型的一致性優于不引入晴朗指數的結果。如表4所示，引入晴朗指數后，單元模型XGBoost、LightGBM、RFR、SVR和集成模型的R2和RMSE均具有顯著提升，其中RMSE最大降低了0.028 mm/h，最優值為0.037 mm/h。R2最大提高了0.03，最優值為0.985。

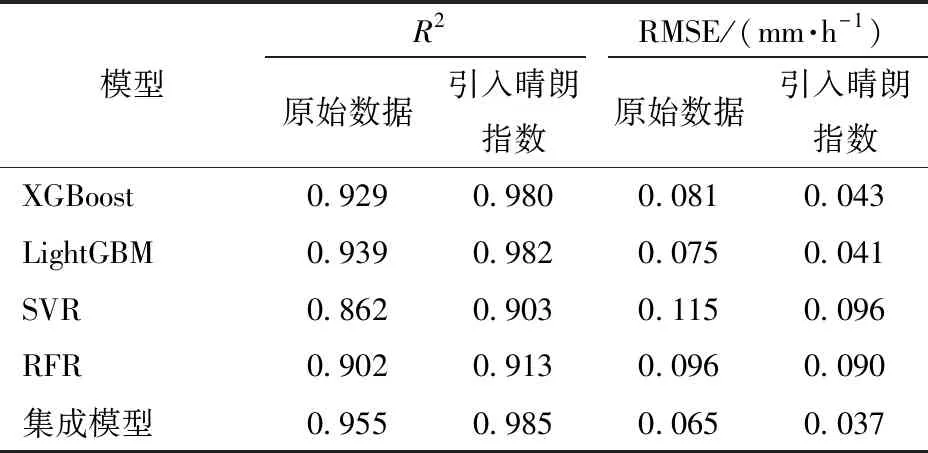
表4 晴朗指數對蒸散量預測模型的影響Tab.4 Influence of sunny index on evapotranspiration prediction model

為了進一步驗證引入晴朗指數后通過光照度預測蒸散量的效果以及集成模型在進行蒸散量預測的優勢，采用太陽輻射、晴朗指數和基礎氣象因子作為數據集，通過4種單元模型和集成模型進行蒸散量預測建模并與基于光照度的模型進行對比。

表5為引入晴朗指數后光照度與太陽輻射預測蒸散量的模型結果對比。結果表明：光照度在蒸散量的預測中可代替凈輻射參數。晴朗指數對預測逐時級的實際蒸散量有較大的特征貢獻，提高了預測模型的精度。集成模型的預測能力在蒸散量預測中優于單元模型。基于光照度數據，引入晴朗指數后的數據集成模型預測效果如圖8所示，從圖中可以看出，基于光照度的集成模型在不同天氣晴朗條件下均能很好地表達蒸散量的氣象特征，提高了蒸散量的預測精度。R2和RMSE分別為0.985和0.037 mm/h，能較好地對實際蒸散量進行預測。

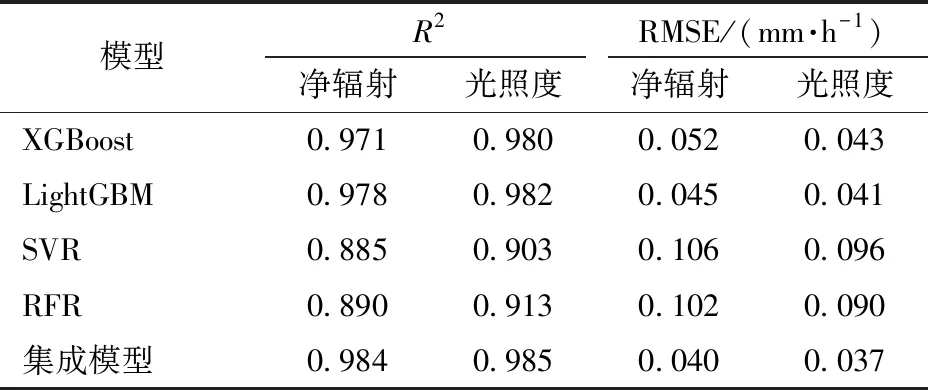
表5 引入晴朗指數后光照度與太陽輻射預測蒸散量 模型對比Tab.5 Comparison between illuminance and solar radiation prediction evapotranspiration model after introducing sunny weather index

3 結論

(1)建立了基于光照度的蒸散量估算方法，分析了光照度代替太陽輻射的可行性，對比了XGBoost、LightGBM、RFR和SVR 4種單元機器學習回歸模型和基于這4種單元模型的集成模型在蒸散量估算中的精度和穩定性。

(2)提出了基于光照度的晴朗指數，晴朗指數有助于表述當日逐時光照度分布差異較大時其逐時蒸散量也存在較大差異這一數據特征，晴天、多云以及陰天等不同天氣條件下蒸散量的變化具有很明顯的特征差異，原始氣象數據中并無對天氣類型的描述，因此降低了模型的預測效果，而晴朗指數作為短期逐時級實際蒸散量預測的懲罰因子解決了此問題，提高了蒸散量的估算精度。

(3)通過光照度代替太陽輻射的可行性分析可以得出，光照度能很好地代替太陽輻射來表述太陽對農田的輻射作用。光照度傳感器使用比較普及，從而降低了農田蒸散量的儀器測量成本。相較于單元模型，集成算法更適合進行蒸散量的估算，集成算法通過次學習器對基礎學習器的4種單元回歸算法特征進行了權值分配，提高了模型的整體精度和穩定性。