基于有限位置法的沖壓機構擺動力完全平衡設計

沈惠平 聶亞彪 李 菊 楊廷力

(常州大學現代機構學研究中心， 常州 213016)

0 引言

實現擺動力和擺動力矩平衡是高速機構設計必須考慮的問題。國內外學者提出了機構擺動力和擺動力矩完全平衡的一些理論和研究方法[1-7]。

BERKOF等[8]提出了線性獨立矢量法，并給出了一般平面機構擺動力完全平衡條件的求解步驟；文獻[9]提出了質量靜替代法，通過對機構各桿件質量的重新分配，實現了一平面四桿機構的擺動力完全平衡；BAGCI[10]通過在機構中附加桿組或子機構的方法，實現了對某些特殊機構的擺動力平衡；文獻[11-12]提出了質量矩替代法，通過將機構中所有連枝構件的質量矩均轉換為與之相鄰的樹枝構件的質量矩，推導了所有樹枝構件擺動力平衡條件；BRIOT等[13]提出一種基于機構總質心最優控制的方法，求解了高速機械手的擺動力平衡問題，并通過對不同運動軌跡的數值模擬，驗證了該方法的有效性；OUYANG等[14-15]提出一種通過調整機構運動學參數使機構總質心靜止不動的方法，從而實現其擺動力的完全平衡。CHAUDHARY等[16]以機構擺動力和擺動力矩為目標函數，基于遺傳進化算法(GA)得到了一組最優解，并驗證了該解的有效性；GENG等[17]在不增加機構整體質量的前提下，通過優化機構總質心軌跡，使機構達到了較好的擺動力平衡效果。上述擺動力完全平衡的方法幾乎都是基于解析法導出機構平衡條件，以適應機構運動的任意位置。而有限位置法[18-20]的思路是：如機構在有限個位置(一般為v+f+1，v為獨立回路數，f為自由度)上擺動力完全平衡，則機構在任意位置上的擺動力也一定完全平衡。

本文應用有限位置法對降耦優化得到的一種含3個回路的零耦合度平面高速沖壓機構進行擺動力完全平衡設計與分析。

1 拓撲結構分析及樹系統劃分

1.1 拓撲結構分析

圖1為零耦合度(κ=0)平面八桿沖壓機構，是針對文獻[21]中耦合度κ=1的平面八桿沖壓機構(只能求得數值型位置正解)，根據機構拓撲降耦設計方法[22-24]進行拓撲優化設計得到的。

該高速沖壓機構主要由驅動構件1和3個平面Ⅱ級桿組(2、3)、(4、5)、(6、7)組成，其中，機架為0，移動副P1為主沖壓頭，移動副P2為輔助推料器，其余7個關節(A～G)均為轉動副。機構中每一構件都存在一條只由轉動副組成的通路，滿足通路定理[15]，因此，該機構可用配重法實現擺動力完全平衡。

顯然，該機構包含3個獨立回路，每個回路的獨立位移方程數ξLi=3(i=1，2，3)，根據全周自由度公式[25]可得

因此，機構僅需一個原動件，當沖壓機頭P1向下沖壓時，輔助推料器P2完成自左向右的沖壓料自動推送，從而完成沖壓，保證了操作人員人身安全。

3個回路A-B-C(P1)、F-E-D、E-G-P2的約束度分別為

因此，上述3個回路分別構成3個子運動鏈(SKC)，分別為SKC1、SKC2、SKC3，它們耦合度[25]分別為

因機構耦合度為零，機構具有解析式位置正解。

1.2 樹系統劃分

因每個SKC可看作一個完整的樹系統，根據連枝構件選取原則，可將每個SKC的構件進行劃分。

SKC1: A-B-C(P1)中，選取構件3為連枝構件，構件1、2為樹枝構件。

SKC2: F-E-D中，選取構件5為連枝構件，構件4為樹枝構件。

SKC3: E-G-P2中，選取構件7為連枝構件，構件6為樹枝構件。

由圖1可知，樹枝構件4、6與連枝構件5通過一個復合鉸鏈RE連接，因此，樹枝構件6和連枝構件7又可看作樹枝構件4的子樹系統。

2 位置分析與驗證

應用有限位置法進行機構擺動力完全平衡計算時，需要對機構進行位置分析，故將圖2機構在SolidWorks中建立三維模型。

2.1 參數設置

桿件長度：lAB=l1=40 mm，lBC=l2=113.14 mm，lDE=l3=170 mm，lEF=l4=109 mm，lEG=l5=109 mm。機架長度：lm=235 mm，ln=205 mm。

設平衡前各桿為質量均勻分布，即除三副桿2之外，其余各桿質心都位于其連桿直線上，即質心參數qi(i=1,3，4，…，7)均為零。

由建立的SolidWorks模型可知，各桿件其他質心位置參數為p1=20 mm，p2=56.83 mm，q2=11.59 mm，p3=0，p4=48 mm，p5=79 mm，p6=48 mm，p7=0。各桿件質量為m1=0.001 kg，m2=0.007 kg，m3=0.006 kg，m4=0.003 kg，m5=0.004 kg，m6=0.003 kg，m7=0.006 kg。其他參數：三副桿2為等腰直角(α=45°)，且lBC=lCD=80 mm，θ3表示構件3與機架的夾角，恒為90°；θ7表示構件7與機架的夾角，恒為0°，未在圖中標出。

2.2 位置參數求解

由圖2可知，點A、B、C、E、G坐標為A=(lm，ln)、B=(lm+l1cosθ1，ln+l1sinθ1)、C=(lm，By-l2sinθ2)、E=(Fx+l4cosθ4，Fy+l4sinθ4)、G=(2l4cosθ4，0)。

已知θ1為驅動角，易求得構件2、4、5、6的角位置θ2、θ4、θ5、θ6分別為

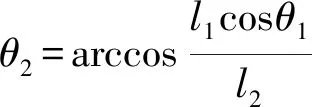
其中

利用Matlab編程計算和ADAMS仿真計算，驗證了上述位置求解公式的正確性，為求解各樹枝構件的配重參數奠定了基礎。

3 擺動力完全平衡求解

3.1 有限位置法的基本原理及求解步驟

對于基本回路數為v、自由度為f的平面機構，為實現擺動力完全平衡，需對該機構中(v+f)個樹枝構件添加配重；機構擺動力完全平衡時，機構在任意位置上總質量矩為同一常量，故任取機構(v+f+1)個位置上總質量矩，便可建立(v+f)個線性方程組，則機構中(v+f)個配重參數便可求解。

通過有限個位置上的質量矩導出的平衡參數，也同樣適用于機構運動的其他任意位置。該方法的特點在于，完成機構位置分析后，取有限個(v+f+1)位置的數值結果建立線性方程組，即可求解得擺動力平衡條件。

為便于理解，給出有限位置法的主要求解步驟，如圖3所示。

3.2 各構件參數fi、gi

(1)SKC1: A-B-C(P1)的質量矩求解

構件1、2、3質量矩分別為

(1)

(2)

(3)

由式(1)～(3)相加，可得SKC1質量矩為

(4)

式中M1——SKC1總質量

R1x、R1y——SKC1在x、y方向上的質心位置

(2)SKC2:F-E-D的質量矩求解

構件4、5質量矩分別為

(5)

(6)

由式(5)、(6)相加，可得SKC2質量矩為

(7)

其中M2=m4+m5Cs2x=0Cs2y=0

式中M2——SKC2總質量

R2x、R2y——SKC2在x、y方向上的質心位置

(3)SKC3:E-G-P2的質量矩求解

構件6、7質量矩分別為

(8)

(9)

由式(8)、(9)相加，可得SKC3質量矩為

(10)

其中M3=m6+m7Cs3x=0Cs3y=0

fi=2l4cosθ4+mipigi=2l4sinθ4+miqi

式中M3——SKC3總質量

R3x、R3y——SKC3在x、y方向上的質心位置

進一步，由式(4)、(7)、(10)，得到整個機構質量矩為

(11)

其中

Cx=∑CsxCy=∑Csy

式中M——機構總質量

Rx、Ry——機構總質心位置

各個構件的平衡參數fi、gi(單位:kg·mm)為

(12)

(13)

(14)

(15)

(16)

(17)

(18)

由式(15)可知，構件4的f4、g4，除了與本身質量參數有關，同時還會受到構件5、6、7的影響，這也表明，在樹系統劃分中，樹枝構件6和樹枝構件7組成的SKC3，被看作是樹枝構件4的子樹系統，其子樹系統質量矩會影響其質量矩。

3.3 配重參數求解

機構動力平衡時，機構在任意位置上總質量矩相等，由式(11)可知，該機構總質量矩是一個關于θi(i=1,2，…,7)的函數，取機構在5個不同運動位置(v+f+1=5)，各構件角位置記為θik(i表示構件編號，k表示機構運動位置編號，k=0,1，2，3，4)，將θik代入式(11)，可得

(19)

式中MRxk、MRyk——第k個運動位置上機構總質量矩x、y方向上的分量

若取機構中(v+f)個合適的構件((v+f)指整個機構中所有樹枝構件的數目)，并附加以適當的配重，使機構擺動力完全平衡，即其總質量矩為常量，則由式(19)可知

(20)

將式(19)代入式(20)，可得

(21)

其中 ΔCik=cosθik-cosθi0ΔSik=sinθik-sinθi0

為便于計算機編程和求解，將式(21)改寫成矩陣形式

(22)

其中

ΔCⅡ、ΔSⅡ的形式類比于ΔCⅠ、ΔSⅠ，下標Ⅰ表示樹枝構件的位置參數，下標Ⅱ表示連枝構件的位置參數。

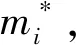
(23)

其中

FⅠ=[f1f2f4f6]T

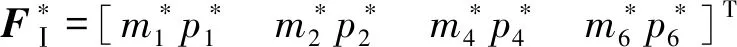
3.4 數值求解

任取機構5個(v+f+1=5)運動位置，即當主動輸入角θ1分別為10°、20°、30°、40°、50°時，可求得各構件的角位置變化，并將其代入ΔCⅠ、ΔSⅠ、ΔCⅡ、ΔSⅡ中，可得

將式(12)～(18)及上述求得的ΔCⅠ、ΔSⅠ、ΔCⅡ、ΔSⅡ代入式(23)中，即可求得所有樹枝構件的配重參數為

(24)

(25)

(26)

(27)

當主動輸入轉角θ1分別為30°、60°、90°、120°、150°時，得到各樹枝構件的配重參數，和式(24)～(27)計算結果一致，證明了有限位置法的正確性。

4 配重參數敏感度分析及機構平衡分析

敏感度用來衡量機構中某個變量對最終結果的影響程度，敏感度越大表示該變量對最終結果影響較大；一般選擇敏感度大的變量進行優化和調整。

4.1 配重參數對總質心軌跡的影響

機構擺動力完全平衡的充要條件是：機構總質心靜止不動，即質心軌跡所圍成的面積越小，則表示機構質心越穩定。

4.2 配重參數對總慣性力的影響

機構總慣性力為

(28)

4.3 設計變量選取及部分平衡設計

由圖8a可知，平衡前后x軸方向的質心軌跡波動極差(最大值與最小值之間的差距)分別為23.4、13 mm，后者比前者優化了44.44%。由圖8b可知，平衡前后y軸方向的質心軌跡波動極差為42.04、16.91 mm，后者比前者優化了59.78%。由圖8c可知，平衡前機構總質心軌跡所圍成面積較大，而平衡后的面積卻很小，表明了平衡后機構總質心更加穩定，特別是在y軸方向上波動明顯減小。

由圖9a可知，平衡前后機構總慣性力在x軸方向的極差分別為0.654、0.177 kg·mm，后者比前者波動減小72.94%。由圖9b可知，平衡前后機構總慣性力在y軸方向的最大極差分別為0.37、0.35 kg·mm，后者比前者波動減小5.40%。由圖9c可知，平衡前后機構總慣性力的最大極差分別為0.426、0.293 kg·mm，后者比前者波動減小31.22%。

可見，有限位置法的擺動力平衡效果較為有效。

5 結論

(1)采用有限位置法對具有兩個末端執行器的零耦度平面高速沖壓機構進行了動平衡計算，得到了機構擺動力完全平衡條件，并對其進行了數值求解驗證。