中壓直流配電系統等效降階建模及控制參數設計

朱 琳，趙學深，王一振，郭 力，劉海濤，袁宇波，盧 浩

（1. 天津大學 智能電網教育部重點實驗室，天津300072；2. 天津市智慧能源與信息技術重點實驗室，天津300072；3. 中國電力科學研究院有限公司，北京100192；4. 國網江蘇省電力有限公司電力科學研究院，江蘇 南京210096）

0 引言

相較于傳統中壓交流配電系統而言，中壓直流MVDC（Medium Voltage DC）配電系統在能源效率、配電容量、配電損耗、建設成本等方面具有明顯的優勢，所以MVDC 配電系統是未來配電系統的發展趨勢［1-2］。恒功率負荷的負電阻特性、控制參數不合理等因素都可能會導致MVDC配電系統出現穩定性問題［1-4］，為此采用準確的穩定性分析模型以及控制參數設計方法是十分有必要的。雖然全階模型能夠詳細描述直流系統的動態特性，但建模過程復雜，模型階數也比較高，難以直接指導控制參數設計［3-4］。因此，為降低直流系統動態特性分析的復雜性，降階建模是非常有必要的［5-8］；同時，為盡量避免因控制參數不合理而導致直流系統出現穩定性問題［9］，以整個直流系統動態特性為設計目標的控制參數設計方法得到了國內外學術界和工業界的廣泛關注［10-12］。

準確的直流系統等效降階模型是開展系統動態特性分析的基礎。利用常規降階建模方法得到直流系統降階模型的過程可大致分為2 步。第1 步為建立各個換流器在其單獨運行時的閉環降階模型。文獻［5］中，在換流器單獨運行時的電壓控制帶寬遠高于下垂控制的前提下，電壓控制參數就可以被忽略，進而換流器就可以等效降階為輸出電壓由下垂控制器所決定的受控理想直流電壓源。然而，當上述前提不成立時，所建立的換流器降階模型將無法準確反映實際情況。第2 步為利用系統拓撲將各個換流器閉環降階模型連接起來以建立整個直流系統的閉環降階模型。文獻［8］基于換流器的RLC 降階模型，結合系統拓撲建立了直流系統降階模型（二階模型），并從解析的角度分析了電壓PI 控制參數等因素對系統動態特性的影響。文獻［9］辨識了電壓源換流器（Voltage Source Converter）的主導特征根中參與度較高的狀態變量，然后基于瞬時功率理論建立了換流器新型降階模型，最后結合配電系統拓撲建立了11 階的直流配電系統降階模型。綜上所述，利用常規降階建模方法能夠建立用于評估直流系統動態特性的閉環降階模型，但很難為以整個直流系統動態特性為設計目標的控制參數設計提供必要的開環降階模型支撐。

控制參數是決定直流系統動態特性的關鍵因素。換流器在單獨運行時的控制參數設計方法已經非常成熟，所以換流器在單獨運行時一般不會出現穩定性的問題。但當多個換流器構成一個直流系統時，各換流器間就會存在動態交互，另外恒功率負荷的負電阻特性會減小系統阻尼，多方面因素的疊加可能最終導致系統出現穩定性問題。針對上述因素所造成的直流系統穩定性問題，文獻［11］基于所提出的模塊化多電平換流器降階模型，提出了一種能夠有效提高直流系統穩定性的附加阻尼控制方法；在此基礎上，文獻［12］提出了提高換流器運行性能的附加功率阻尼控制方法。雖然文獻［11-12］提出的方法能夠有效解決直流系統出現的穩定性問題（該穩定性問題可以通過優化控制參數主動規避［9］），但以整個直流系統動態特性為目標的控制參數設計方法鮮有介紹。基于所建立的直流系統降階模型，文獻［13］提出了一種直流系統電壓控制器參數設計方法，實現了直流系統振蕩頻率及阻尼比的定性定量設計，但僅討論了換流器參數完全相同時的場景，并沒有討論各個換流器間參數不一致的情況。

針對上述問題，本文以MVDC 配電系統為研究對象，基于所提出的開閉環逐步等效降階建模方法，逐步建立計及換流器間動態交互的開環和閉環等效降階模型，并利用狀態反饋控制方法以及所提出的MVDC 配電系統控制參數設計方法實現系統振蕩頻率及阻尼比的定性定量設計。首先，建立了MVDC配電系統的等效降階電路模型以及計及換流器間動態交互的開環等效降階模型；其次，建立了計及換流器間動態交互的閉環等效降階模型，并提出了一種MVDC 配電系統控制參數設計方法；然后，以某MVDC 配電系統為例進行了控制參數的定性定量設計；最后，基于RT-BOX 硬件在環實驗平臺，驗證了理論分析的合理性。

1 計及換流器間動態交互的開環等效降階模型

1.1 系統拓撲及其等效電路模型

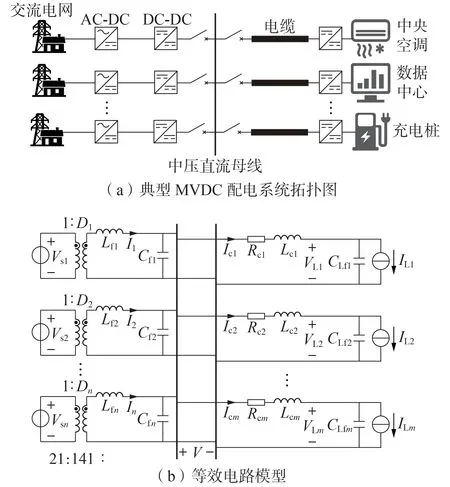
圖1 典型MVDC配電系統拓撲及其等效電路模型Fig.1 Topology of typical MVDC distribution system and its equivalent circuit model

對如圖1（a）所示的MVDC配電系統中的相關電力電子裝置進行等值處理，得到如圖1（b）所示的MVDC配電系統等效電路模型［14］。圖1（b）中，Vsk（k=1，2，…，n，其中n為VSC 的臺數）為第k臺DC-DC VSC（即VSCk）的理想直流輸入電壓源；Dk和Ik分別為VSCk的占空比和輸出濾波電感電流；Lfk和Cfk分別為VSCk的輸出濾波電感和輸出濾波電容；V為直流母線電壓；Rch和Lch（h=1，2，…，m，其中m為恒功率負荷的個數）分別為第h條電纜線路的線路電阻和線路電感；Ich和ILh分別為第h條電纜線路上的電流和注入到第h個恒功率負荷的電流，其中ILh可為正值或負值，為正值時表示是真正的恒功率負荷，為負值時表示是風機和光伏等可再生能源［8，14］；CLfh和VLh分別為第h個恒功率負荷的輸入濾波電容和輸入電壓［14］。由此，圖1（b）所示的MVDC 配電系統等效電路模型可由n+2m+1階微分方程描述。

1.2 等效降階電路模型

當用等效簡化模型［3］表示多個并聯運行的恒功率負荷時，圖1（b）可以被簡化為圖2（a）。基于開閉環逐步等效降階建模方法的第1 步，并利用戴維南和諾頓等效定理，將圖2（a）等效為圖2（b）所示的等效降階電路模型。圖2 中，Cfeq為所有輸出濾波電容Cfk并聯后的等效輸出濾波電容；CLfeq為所有輸入濾波電容CLfk并聯后的等效輸入濾波電容；Rcable和Lcable分別為等效電纜線路的線路電阻和線路電感［3］；Vseq為理想直流輸入電壓源；Leq為等效輸出濾波電感；IL為等效恒功率負荷的電流，即所有恒功率負荷電流ILh的累加；Peq為等效恒功率負荷功率；Deq為等效降階模型的占空比；I為等效降階模型的輸出濾波電感電流。

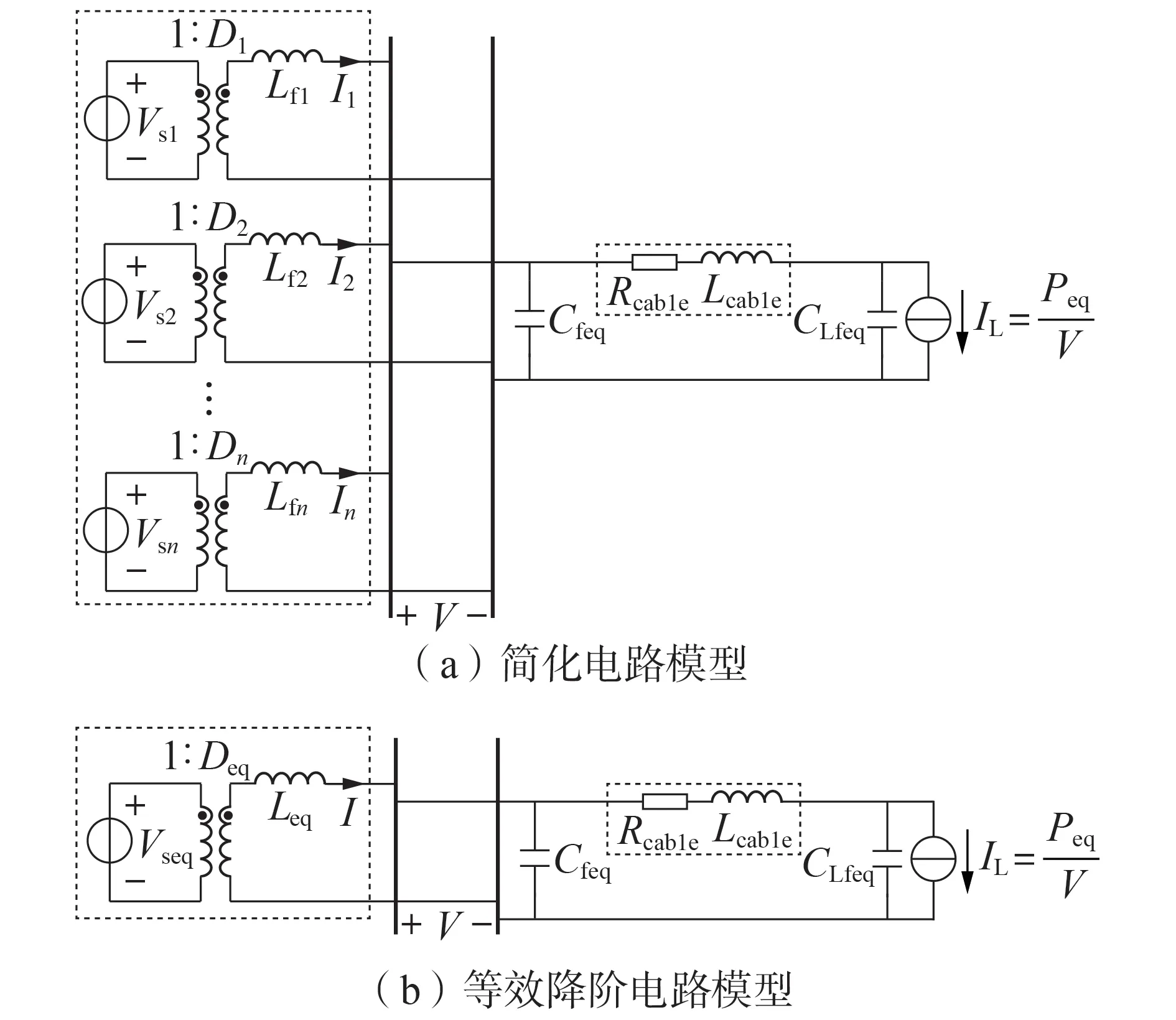
圖2 簡化電路模型及其等效降階電路模型Fig.2 Simplified circuit model and its equivalent reduced-order circuit model

其中，ω0和ζ0分別為MVDC 配電系統的無阻尼自然頻率和阻尼比；ωcz和ζcz分別為電纜線路引入零點所對應的固有振蕩頻率和阻尼比；ωcp和ζcp分別為電纜線路引入極點所對應的固有振蕩頻率和阻尼比；Ceq為等效輸出濾波電容。

傳遞函數Gvdk_cable(s)的幅頻曲線如圖3 所示。圖中，f0=ω0（/2π）；fcz=ωcz（/2π）；fcp=ωcp（/2π）。

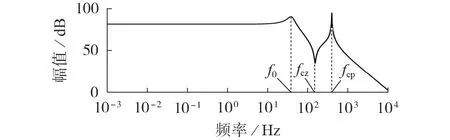
圖3 傳遞函數Gvdk_cable（s）的幅頻曲線Fig.3 Magnitude-frequency curve for transfer function Gvdk_cable（s）

由圖3和式（3）可知，ωcz由Lcable和CLfeq共同決定，并不會受到MVDC 配電系統中控制參數的影響［15］。當ωcz與ω0間的比值小于5 倍頻時，電纜線路就會對MVDC 配電系統的動態特性造成負面影響，嚴重時可導致系統出現穩定性問題。此時，可以利用狀態反饋控制解決該問題［14］，具體內容將在第2 節進行詳細介紹。由自動控制原理可知，當ωcz與ω0間的比值大于5 倍頻時，電纜線路的影響就可以被忽略［16］。當忽略電纜線路時，圖2 中的Cfeq和CLfeq就并聯得到Ceq，此時MVDC 配電系統中的多個濾波環節最終可等效降階為一個LC濾波環節。

對 于VSCk而 言，Dk(s)至V的開 環傳遞 函數Gvdk(s)的表達式就會變為：

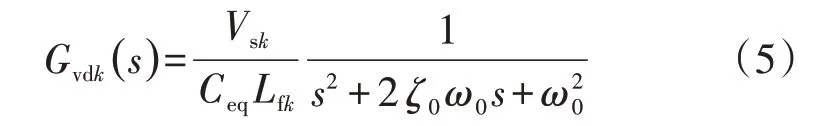
開環傳遞函數Gvdk(s)就是VSCk的計及換流器間動態交互的開環等效降階模型，不僅計及了VSCk自身的濾波參數，還計及了其他換流器的濾波參數。由式（2）可知，ζ0<0，說明MVDC 配電系統的等效降階電路模型存在2個不穩定的極點，后續將在第2節介紹如何設計控制參數保證MVDC 配電系統的穩定性。

2 計及換流器間動態交互的閉環等效降階模型及控制參數設計

利用開閉環逐步等效降階建模方法的第2 步和第3 步，建立計及換流器間動態交互的閉環等效降階模型，如圖4所示。

由圖4 可知，利用開閉環逐步等效降階建模方法可得到MVDC配電系統（多個VSC并聯）最終的等效降階模型（單個VSC）。考慮到MVDC 配電系統中各VSC 通過下垂控制來實現功率分配，故等效降階模型的控制結構中也配置了下垂控制。另外，MVDC 配電系統及其等效降階模型的控制結構中均包含狀態反饋控制環節，其原因將在2.1 節詳細闡述。

2.1 計及狀態反饋控制的等效降階建模

本文采用狀態反饋控制方法主要是基于以下2個方面的考慮［14］。一方面，因恒功率負荷的負電阻特性，傳遞函數Gvdeq(s)呈現負相的不穩定狀態，并且電壓PI 控制器并不能有效改變電壓控制回路增益相角裕度。本文所采用的基于泰勒展開的狀態反饋控制方法的優勢在于能將傳遞函數Gvdeq(s)控制成含正相穩定狀態的傳遞函數Gsvdeq(s)，滿足了MVDC配電系統對穩定性的需求。另一方面，當ωcz與ω0間的比值小于5 倍頻時，電纜線路會對MVDC 配電系統的動態特性造成負面影響，嚴重時可導致系統出現穩定性問題。此時，可利用基于泰勒展開的狀態反饋控制方法將無阻尼自然頻率ωf調整至合理值，以滿足上述要求。利用所建立的計及換流器間動態交互的閉環等效降階模型中的狀態反饋控制傳遞函數頻域曲線，就可以查看狀態反饋控制的效果。特別說明，雖然ω0和ωf都是無阻尼自然頻率，但ω0僅由濾波參數決定（見式（2）），而ωf則由濾波參數和狀態反饋系數共同決定（見式（14））。

由圖4（a）可知，MVDC 配電系統中各個VSC 均配置了狀態反饋控制。計及狀態反饋控制后的VSCk占空比Dk(s)變為：

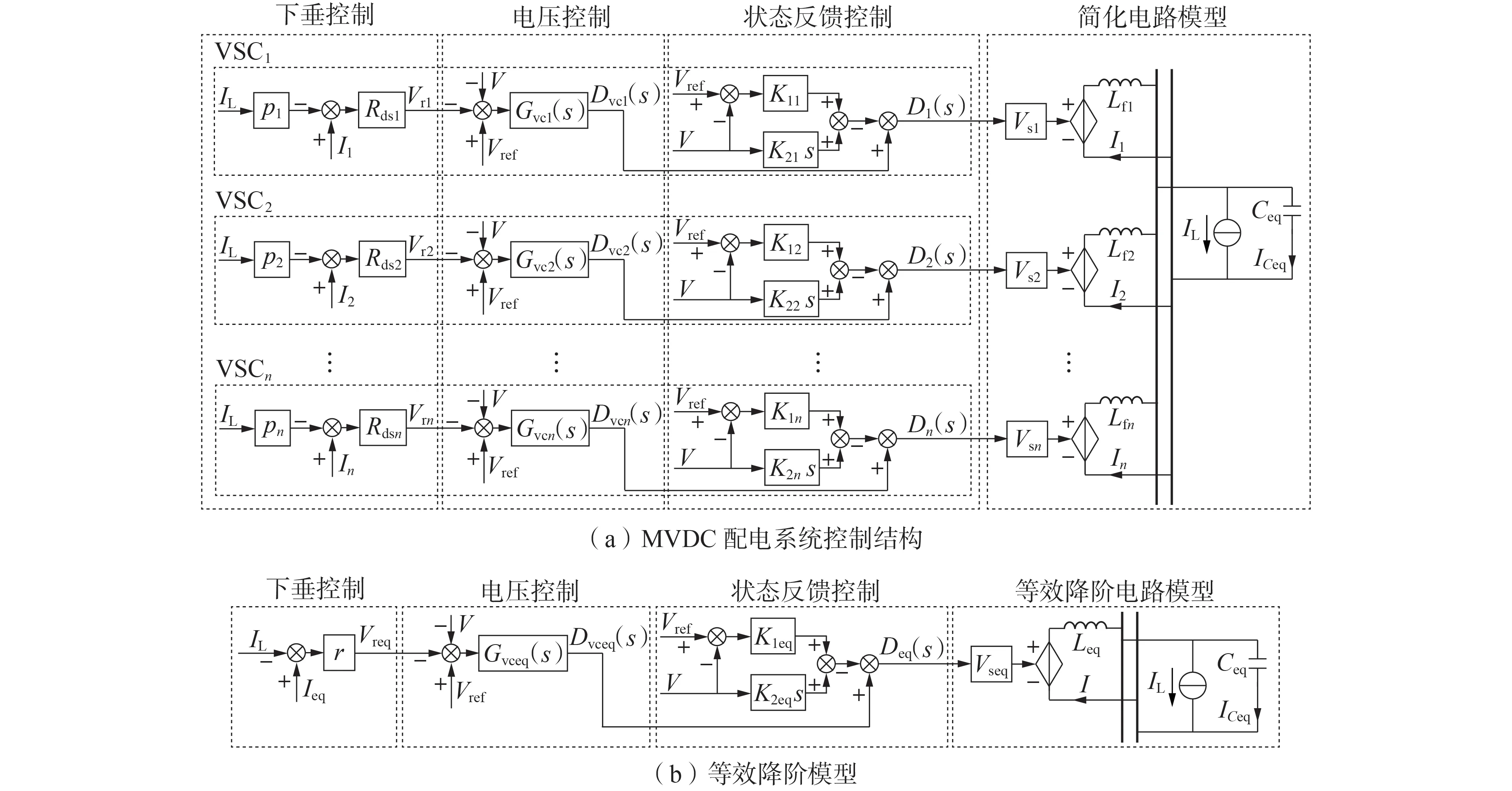
圖4 MVDC配電系統控制結構及其等效降階模型Fig.4 Control structure of MVDC distribution system and its equivalent reduced-order model

由式（9）可知，Gsvdk(s)就是VSCk的計及換流器間動態交互的閉環等效降階模型中的狀態反饋控制傳遞函數。Gsvdk(s)不僅計及了VSCk自身的狀態反饋增益，還計及了其他換流器的狀態反饋增益。

聯立式（6）和式（11），Dvceq(s)至V的傳遞函數Gsvdeq(s)的表達式變為：

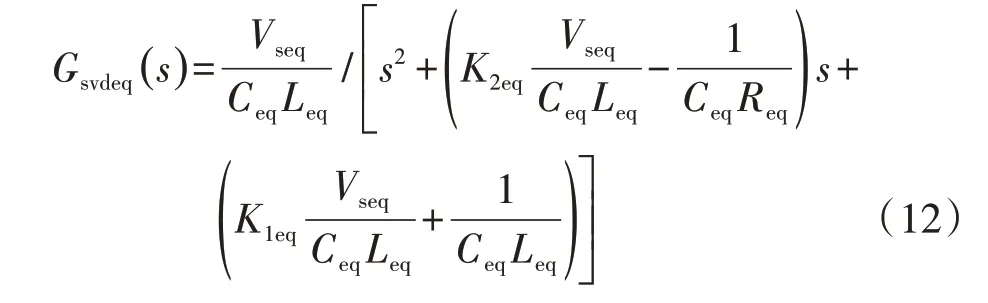
式（12）可以寫成如式（13）所示的典型二階系統形式。

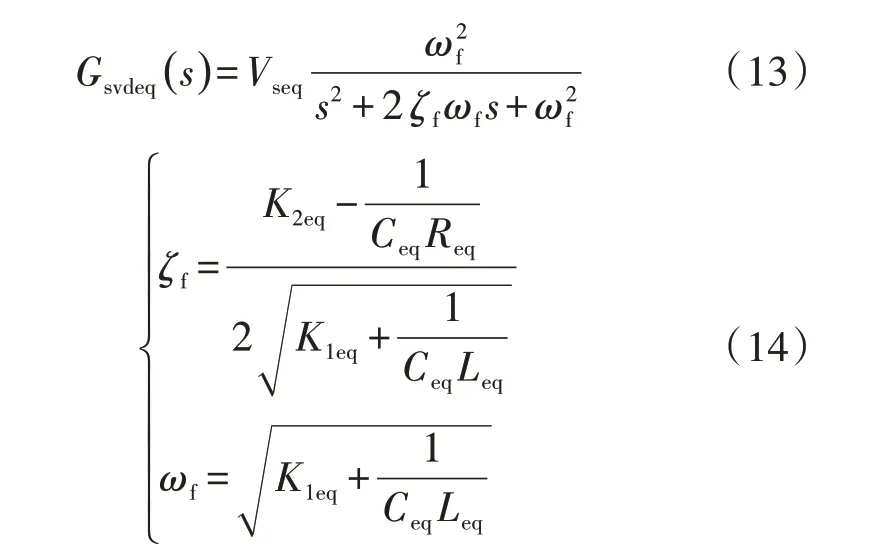
其中，ωf和ζf分別為無阻尼自然頻率和阻尼比。

由式（14）可知，可調整K1eq和K2eq使得ζf為合適的正值，同時也可以改變ωf以滿足系統振蕩頻率設計需求。

若Vsk均為相同常數值，并且假設Gsvdeq(s)等于所有Gsvdk(s)之和，則存在式（15）成立。

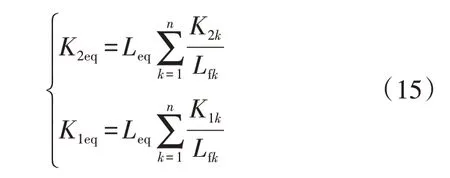
當已知各VSC 狀態反饋增益時，可通過式（15）計算得到等效降階模型的狀態反饋增益，并利用傳遞函數Gsvdeq(s)就能夠反映MVDC 配電系統中傳遞函數Gsvdk(s)的整體特性。

2.2 計及電壓控制及下垂控制的等效降階建模

由圖4（a）可知，計及電壓控制和下垂控制后，VSCk的占空比Dk(s)的表達式進一步變為：

2.3 MVDC配電系統控制參數設計方法

基于所建立的計及換流器間動態交互的開環和閉環等效降階模型，并為達到將MVDC 配電系統控制成二階系統（即精準設計系統振蕩頻率和阻尼比）的目的，本文提出了一種MVDC 配電系統控制參數設計方法，共包含如下3步。

第1 步，計算狀態反饋增益。根據預設的無阻尼自然頻率ωf和阻尼比ζf，計算各VSC 的狀態反饋增益。

第2 步，根據各VSC 電壓控制回路增益的穿越頻率，設計各VSC 電壓PI 控制器的比例增益和積分增益（積分增益與比例增益的比值通常為電壓控制回路增益穿越頻率的1/10）。為獲得足夠的相角裕度，電壓控制回路增益的穿越頻率與ωf間的比值應稍微大于1（本文取1.2），但穿越頻率也應同時小于開關頻率的1/10。基于所確定的穿越頻率，利用所建立的計及換流器間動態交互的閉環等效降階模型中的電壓控制傳遞函數，就可以計算得到各VSC 電壓PI控制器的比例增益和積分增益。

第3步，計算MVDC配電系統所對應二階系統的振蕩頻率及阻尼比。根據式（4）、（15）和（23）計算得到等效降階模型的濾波參數和控制參數，并通過計算電壓閉環傳遞函數Gsivveq(s)的零、極點來確定MVDC配電系統所對應二階系統的振蕩頻率和阻尼比。

3 案例分析

基于上文所介紹的等效降階模型以及MVDC配電系統控制參數設計方法，以附錄中圖A5所示的MVDC 配電系統為例，開展案例分析工作。基于MVDC 配電系統的直流電壓紋波V%k=1%和直流電流紋波I%k=15%標準［14］，設計電壓等級為10 kV的系統，具體參數如表1 所示。在該MVDC 配電系統中，電纜線路所引入的固有振蕩頻率ωcz≈941 rad／s（約為150 Hz），故只要MVDC 配電系統的振蕩頻率ωs<188 rad／s（約為30 Hz），即當ωcz與ω0間的比值大于5倍頻時，就可以忽略電纜線路的影響［16］。

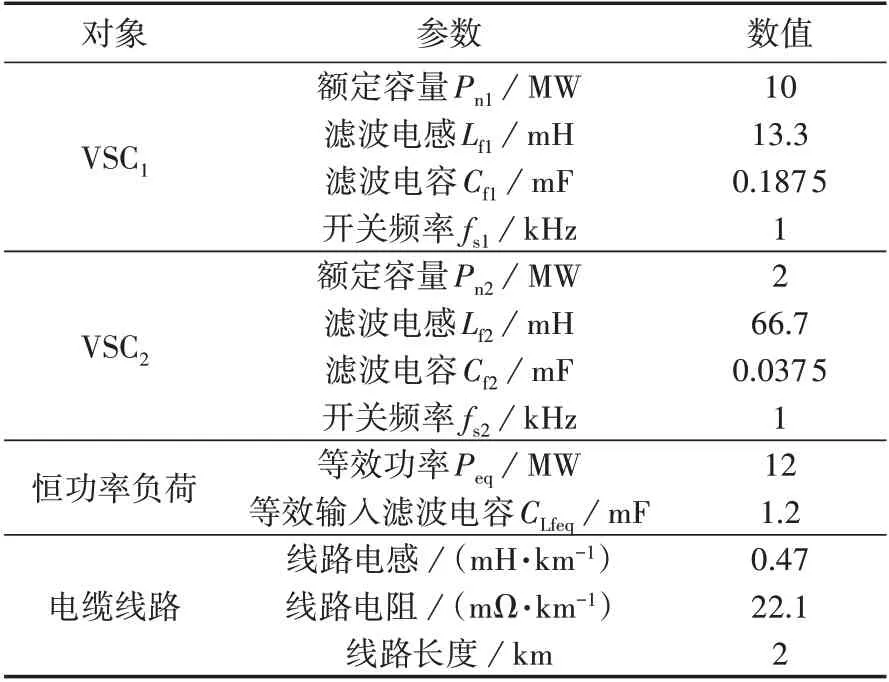
表1 MVDC配電系統參數Table 1 Parameters of MVDC distribution system

下面給出如表2 所示的7 種場景，這7 種場景的零、極點如表3 所示。表中，ff=ωf/（2π）；fs和ζs分別為系統振蕩頻率和阻尼比。

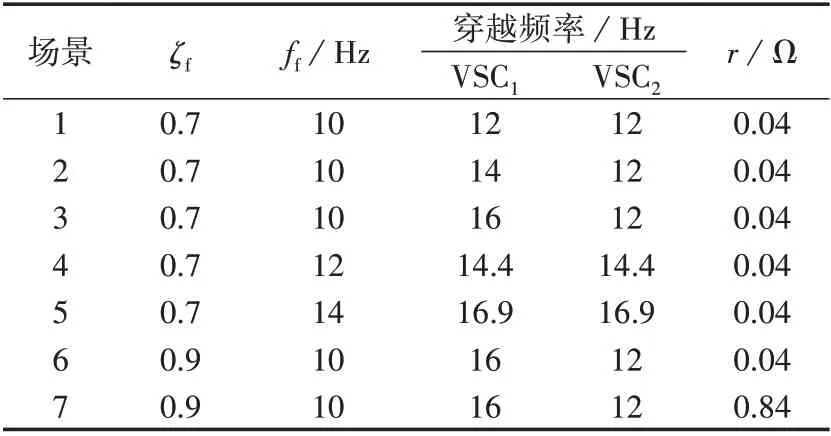
表2 場景設置Table 2 Case setting

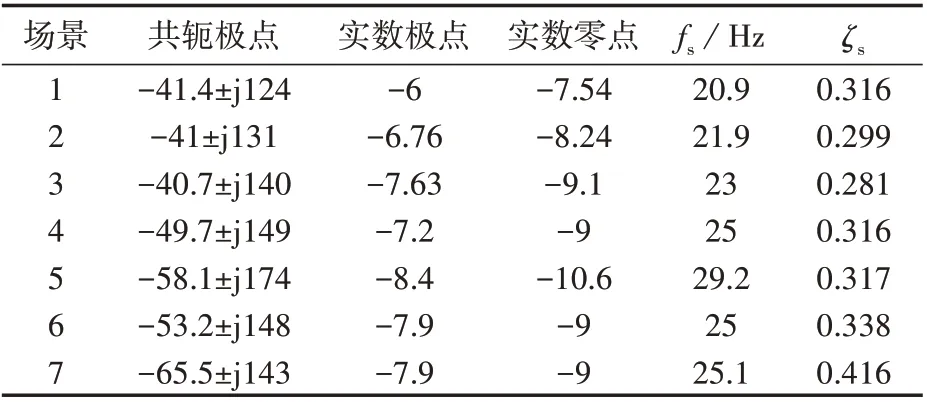
表3 等效降階模型的零、極點Table 3 Zeros and poles of equivalent reduced-order system

由表3 可知，在場景1—7 中，由于實數零點和實數極點的相互抵消作用，MVDC 配電系統均被等效降階為二階系統，只是7 個場景的等效二階系統的振蕩頻率和阻尼比有所差異。

3.1 MVDC配電系統等效降階建模分析

以場景2 為例，驗證所提開閉環逐步等效降階建模方法以及MVDC配電系統控制參數設計方法的有效性。上述降階建模過程是在忽略電纜線路影響的情況下進行的，現以表1 所示的MVDC 配電系統為例進行說明。計及電纜線路后，等效降階模型的相關傳遞函數定義如下：占空比至直流母線電壓的傳遞函數為Gvdeq_cable(s)，計及狀態反饋控制后的占空比至直流母線電壓的傳遞函數為Gsvdeq_cable(s)，電壓控制回路增益為Tsvveq_cable(s)，電壓閉環傳遞函數為Gsvveq_cable(s)。由于計及電纜線路影響的MVDC 配電系統動態特性分析不是本文的研究重點，所以本文不再提供上述4 個傳遞函數的表達式，筆者將在另外的文章中進行詳細闡述。

場景2 下等效降階模型的波特圖如圖5 所示。圖中，fc和γc分別為電壓控制回路增益的穿越頻率和相角裕度；fb和γb分別為電壓閉環傳遞函數的穿越頻率和相角裕度。

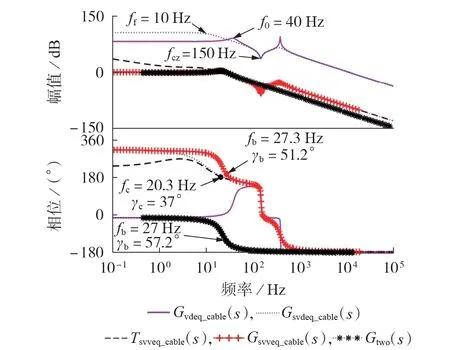
圖5 場景2下等效降階模型的波特圖Fig.5 Bode diagram of equivalent reduced-order system under Case 2

下面以MVDC配電系統中各VSC動態特性存在差異的場景1—3，驗證本文所提開閉環逐步等效降階建模方法以及MVDC配電系統控制參數設計方法的有效性。傳遞函數Tsvv1(s)的波特圖如附錄中圖A1 所示，傳遞函數Gsvveq(s)的零、極點如表3 所示。由圖A1可知，增大fc會減小傳遞函數Tsvv1(s)的相角裕度。在場景1—3中，由于實數零點和實數極點的相互抵消作用，所以MVDC 配電系統的動態特性均可由1 對共軛極點（等效二階系統）進行描述。并且，當增大fc時，雖然會增大等效二階系統的振蕩頻率，但會減小等效二階系統的阻尼比。

3.2 MVDC配電系統振蕩頻率設計及分析

3.1節的設計思路雖能調整系統振蕩頻率，但會改變系統阻尼比。為此，在保持fc與ff間比值不變（以1.2為例）的前提下，通過改變ff來調整系統振蕩頻率。以場景1、4、5 為例，畫出傳遞函數Gvd1(s)、Tsvveq(s)的波特圖如附錄中圖A2 所示，傳遞函數Gsvveq(s)的零、極點如表3 所示。由圖A2 可知，增大ff會增大傳遞函數Tsvv1(s)的穿越頻率（其相角裕度基本保持不變），并會增大等效二階系統的振蕩頻率（阻尼比基本保持不變）。

3.3 MVDC配電系統阻尼比設計及分析

4 實驗驗證

為驗證所提開閉環逐步等效降階建模方法以及MVDC 配電系統控制參數設計方法的有效性，基于附錄中圖A4 所示的RT-BOX 硬件在環實驗平臺搭建了如附錄中圖A5 所示的MVDC 配電系統及等效降階模型的開關模型。實驗系統參數與理論分析參數一致，如表1所示。

4.1 MVDC配電系統等效降階建模驗證

0.1 s 時，恒功率負荷從6 MW 突增至12 MW，場景2下直流母線電壓波形如圖6所示。

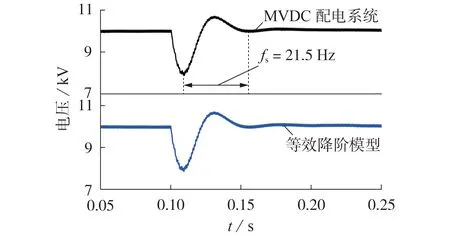
圖6 驗證等效降階建模有效性的實驗波形Fig.6 Experimental waveforms for verifying validity of equivalent reduced-order model

由圖6 可知，MVDC 配電系統及其等效降階模型的直流母線電壓的動穩態特性具有極高的一致性，驗證了本文所提開閉環逐步等效降階建模方法的正確性和適用性。另外，圖6 所示的實驗結果的振蕩頻率約為21.5 Hz，與表3 中21.9 Hz 的理論設計值基本一致，驗證了基于本文所提控制參數設計方法能夠將MVDC配電系統等效降階為二階系統。

4.2 MVDC配電系統振蕩頻率實驗驗證

相同的實驗工況下，場景1、4、5 的實驗波形如附錄中圖A6 所示。由圖可知，MVDC 配電系統及其等效降階模型均呈現出相同的二階系統特性，并且直流母線電壓實驗結果的振蕩頻率及阻尼比與表3中的理論設計值基本一致，驗證了通過改變ff來設計系統振蕩頻率的合理性。

4.3 MVDC配電系統阻尼比實驗驗證

相同的實驗工況下，場景3、6、7 的實驗波形如附錄中圖A7 所示。由圖可知，MVDC 配電系統及其等效降階模型均呈現出相同的二階系統特性，且場景3、6、7 的直流母線電壓超調量逐漸減小，表明MVDC 配電系統阻尼比逐漸增大，驗證了通過增大ζf和r來增大系統阻尼的有效性。

相同的實驗工況下，場景7下2臺VSC的輸出電流波形如圖7 所示。由圖可知，VSC1和VSC2的實際輸出電流大小比值為5（與額定容量比值一致），驗證了下垂控制的有效性。綜上所述，狀態反饋控制及電壓控制能夠實現系統動態調整，而下垂控制能夠完成穩態功率分配。

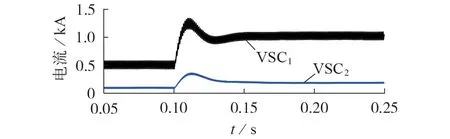
圖7 VSC1和VSC2的輸出電流波形Fig.7 Waveforms of output current of VSC1 and VSC2

5 結論

本文針對MVDC 配電系統等效降階建模及控制參數設計開展了相關研究，得到結論如下。

（1）基于所提出的開閉環逐步等效降階建模方法，建立了計及換流器間動態交互的開環和閉環等效降階模型，并建立了MVDC 配電系統及其等效降階模型間相應參數（濾波參數、狀態反饋控制參數和電壓控制參數）的通用關系表達式。基于等效降階建模方法所建立的等效降階模型的階數，不會受到MVDC 配電系統中VSC 的臺數、濾波參數及控制參數差異性的影響。

（2）基于計及換流器間動態交互的開環和閉環等效降階模型，并利用狀態反饋控制方法以及所提出的MVDC 配電系統控制參數設計方法，在多個場景下均能夠將MVDC配電系統控制成二階系統。無論各個VSC 的濾波參數以及控制參數是否一致，當等效降階模型的電壓閉環傳遞函數頻域曲線呈現出典型二階系統特性時，基于此二階系統所計算得到的振蕩頻率和阻尼比就能夠精確反映出MVDC配電系統的硬件在環時域實驗結果。由多個場景的硬件在環實驗結果可知，MVDC 配電系統及其等效降階模型的直流母線電壓動穩態特性具有高度的一致性。

附錄見本刊網絡版（http：//www.epae.cn）。