基于HJC模型的煤巖沖擊損傷特性研究

劉 錦，李峰輝，劉秀秀

(1.陜西鐵路工程職業技術學院城軌工程學院, 陜西 渭南 714000；2.鄭州市交通規劃勘察設計研究院, 鄭州 450000；3.曲阜遠東職業技術學院, 山東 濟寧 273100)

煤礦生產過程中，無論是巷道的掘進還是煤巖的采動，都會對周邊煤巖施加動態擾動，尤其是爆破工程產生的沖擊，是最為典型的動態加載模式。研究表明[1-13]，動態加載下，巖石材料往往會表現出與靜態加載下截然不同的力學性質。研究不同加載方式下煤巖的變形、強度和破壞機制一直是煤炭工程研究的熱點問題。

Okubo等[1]和Lajtai等[2]通過試驗，研究分析了巖石強度的應變率相關性機制，發現巖石峰值強度與應變率正相關；錢七虎、戚承志等[3-4]結合宏觀黏性和微觀熱活化機理解釋了巖石類材料強度的應變率依賴機制，并建立了相應的強度準則。張文清等[5]通過分形理論研究了沖擊作用下煤巖的破碎特性和耗能規律；薛東杰等[6]研究了加載速率對煤巖采動特性的影響，建立了采動力學條件下考慮加卸載過程中材料損傷的煤巖黏彈性模型屈服準則；劉曉輝等[7]對無煙煤進行了不同應變率下的沖擊壓縮試驗，從能量的角度分析了煤巖的動態力學特性。分離式霍普金森壓桿(SHPB)可以有效地對巖石材料進行中高應變率的沖擊加載[8]，劉少虹等[9]通過改進的SHPB裝置[10]研究了一維動靜組合加載下煤巖的強度特征，認為煤巖體結構特性增強了煤層對動靜載荷的抵抗能力；王文等[11-12]則研究了含水率對煤巖動靜組合力學特性的影響；陸華等[13]研究了循環荷載下不同孔隙率紅砂巖的動力特性和損傷規律。由于沖擊過程極為短暫，且現有試驗手段難以觀測到巖石內部變化，目前對沖擊破壞過程的研究數量較少。隨著人們對數值模擬技術研究的深入，數值模擬已不單純是應力分析的一種手段，也是一種試驗的工具[14]。采用數值試驗可以實現巖石內部變化的即時觀察，是研究沖擊破壞過程的一種有效手段。HJC模型[15]是模擬高應變率、大變形條件下巖石介質力學特性的有效手段[16-18]，該模型同時考慮了巖石的損傷、硬化和屈服特性，且模型參數意義明確，是模擬沖擊作用下煤巖的理想材料模型。方秦等[16]從屈服條件出發，給出了巖石HJC模型參數的確定方法，并給出了Salem石灰巖的HJC模型參數，該方法不但需要進行大量試驗，而且對試驗準確性要求較高；聞磊等[17]、石祥超等[18]將數值模擬手段與試驗手段結合分別研究了花崗斑巖和致密砂巖的HJC模型參數，該方法也能較為準確地得到模型參數，且大大簡化了參數確定過程。

由于煤巖力學性質的離散性，單純依靠試驗手段確定模型參數存在巨大困難，筆者首先通過SHPB試驗裝置對煤巖進行了沖擊壓縮試驗，研究了煤巖動態破壞的特性。然后通過數值試驗數據和實測試驗數據對比，反演了HJC模型的關鍵參數，建立了煤巖的HJC材料模型。最后基于該材料模型模擬了煤巖沖擊破壞，探索性地研究了煤巖的動態破壞過程。

1 煤巖力學特性試驗

分離式霍普金森壓桿(SHPB)試驗裝置是巖石材料動力學試驗的推薦設備，其原理及數據處理方法文獻[19-20]中進行了詳細介紹。本文采用直徑50 mm的SHPB裝置對煤巖進行了單軸沖擊壓縮試驗，以研究煤巖動態強度的應變率相關性。

1.1 試樣的制備

為提高試驗的準確性，減小試件物理力學性質上的離散性，本次試驗使用的試樣均取自同一塊煤巖樣本，該樣本取自陜北神木某煤礦，由于煤巖存在較為明顯的天然裂隙和層理構造，在試樣表面無法避免地存在少量初始裂紋。煤巖體在制作試樣時，其內部裂紋可能出現擴展，對強度的影響也是難以避免的。本文采用剪切波速作為判斷試件質量和完整性的標準，對比制備的試件和原始巖塊的剪切波速，剔除差別較大的試樣。

共制備沖擊壓縮試樣12個，其直徑為50 mm，厚度為25 mm；單軸壓縮試樣3個，其直徑為50 mm，高度為100 mm，單軸靜載試驗采用DDL600多功能試驗機完成，沖擊壓縮試驗采用直徑50 mm SHPB裝置完成。

1.2 試驗方案及結果分析

SHPB沖擊壓縮試驗中，根據氣炮壓力將試件分為3組(每組4個)，對應氣壓分別為0.35、0.50、0.65 MPa，由激光測速儀測得各組的撞擊速度分別為3.54、5.88、8.13 m/s，靜載試驗采用位移控制，應變率不超過10-4s-1。破壞后的煤巖試樣如圖1所示。

圖1 破壞后的煤巖試樣

煤巖的動態破壞特性與靜載作用下的破壞特性有較為明顯的區別，靜載試驗為典型的單一裂紋破壞，即只存在一條主導的破壞裂紋；動載試驗則為多裂紋破壞，同時有多條裂紋貫穿，且沖擊速度越大，貫穿裂紋越多，破碎越嚴重。

分析認為，隨著荷載的增加，試樣薄弱處首先開裂，靜態加載時，應變與應力同步變化，在該裂紋尖端將持續出現應力集中，同時導致周邊應力減小，限制了其他裂紋的有效擴展，形成一條主裂紋。而在高應變率加載條件下，單一缺陷以及其周圍應力降低的區域由于應變傳播速度過慢，來不及阻止其他小的缺陷或者亞缺陷被激活，將會出現多條主要裂紋[20-21]。

SHPB沖擊試驗中采用厚1.2 mm的紫銅片濾波，去除高頻信號，以保持應變率穩定，在入射桿距離試件65 cm和透射桿距離試件40 cm處粘貼電阻應變計，采用超動態應變儀采集電壓信號。將電壓信號轉換為應變信號后。通過三波法[19]對數據進行處理即可得到相應的應變率時程曲線和應力-應變曲線。處理后發現，各組試驗得到的應變率時程曲線存在一定的差異，這與濾波片的選擇有關[22]，本文采用加載過程的平均應變率研究煤巖的動態特性。經計算，各組試驗的平均應變率為42.92、72.92、96.98 s-1，平均抗壓強度為48.75、66.29、84.59 MPa，煤巖的應變率時程曲線和應力-應變曲線，分別如圖2和圖3所示。

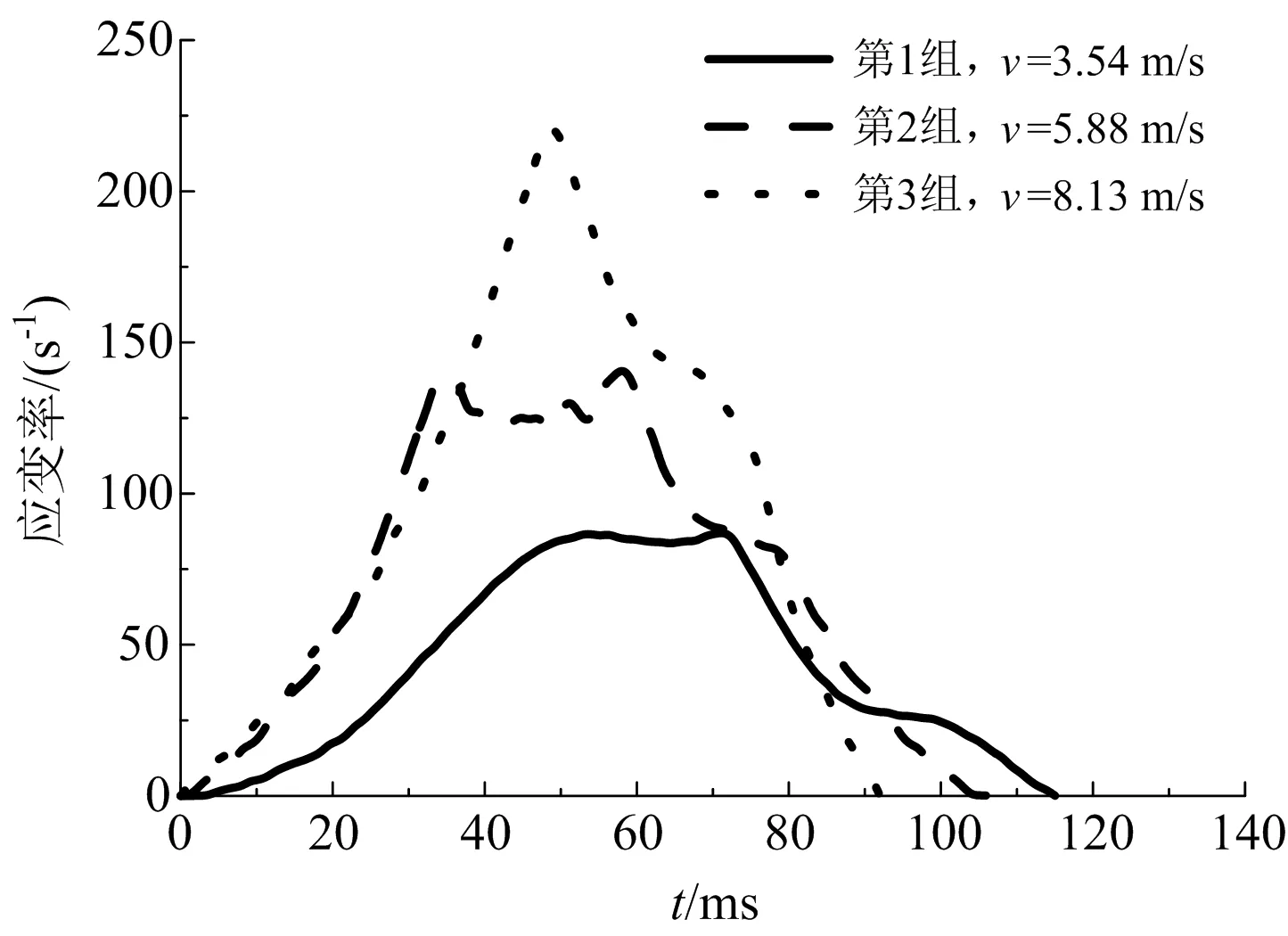
圖2 應變率時程

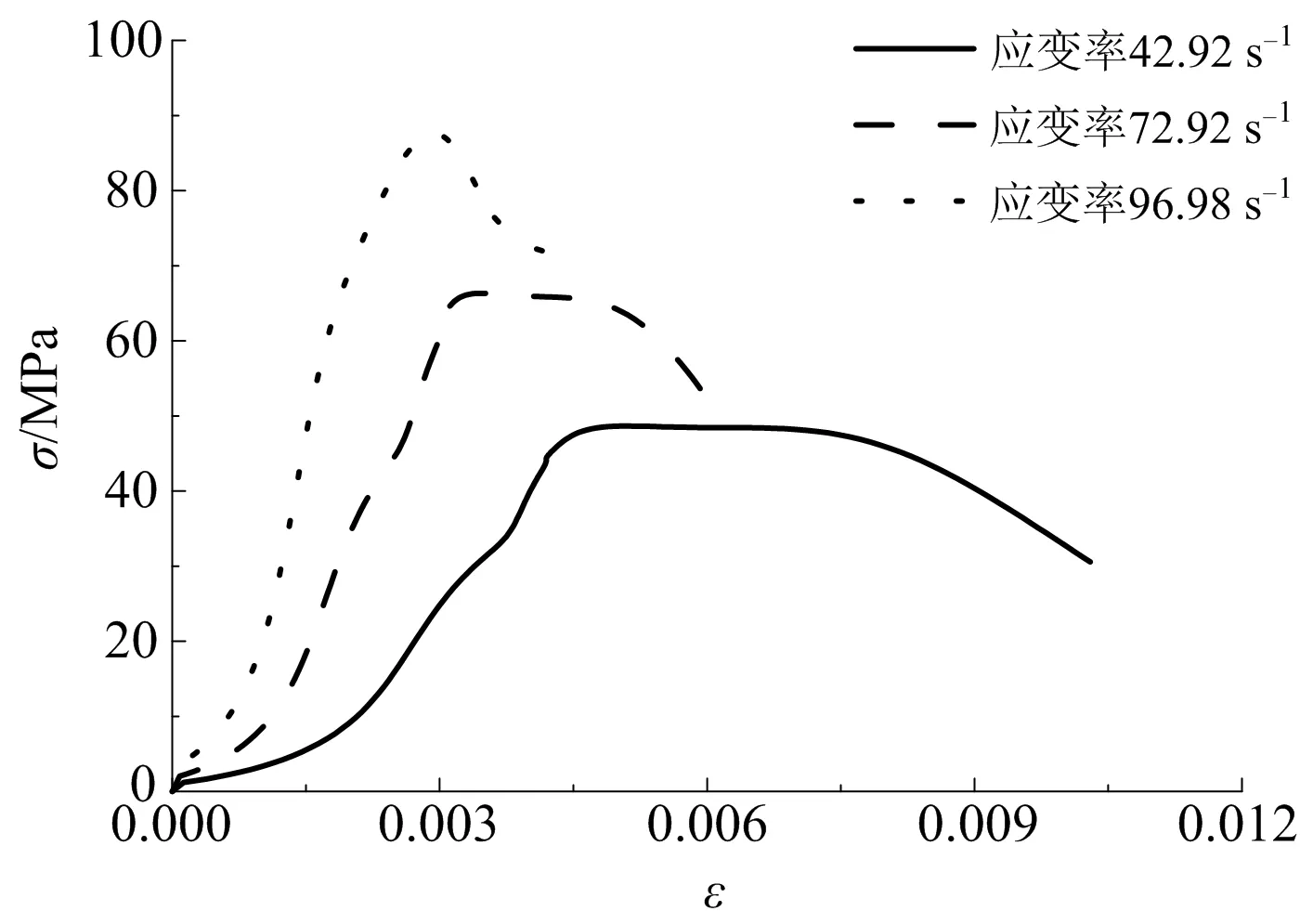
圖3 應力-應變

從圖3中明顯可以看出，煤巖的動態彈性模量隨應變率的增加有較大幅度的提高，表現出明顯的應變硬化的特性；同時極限應變隨應變率的增加出現了下降，說明煤巖的脆性隨應變率增大而顯著增強，這與一般巖石的動力學特性存在顯著差異。

2 煤巖動力學特性試驗模擬

ANSYS/LS-DYNA顯示動力學分析軟件可以用于模擬撞擊、侵徹等問題，其算法豐富，并且支持多種材料模型，是SHPB數值試驗的理想平臺。

2.1 材料模型的選擇

以往的數值模擬都是在已知材料本構關系的基礎上，完成對具體工程的模擬，是“知因求果”。而數值試驗是為了研究材料模型的適用性，確定模型參數，是基于特定材料模型的一種模型擬合或參數反演，屬于“執果尋因”。當數值試驗與試驗取得一致效果時，就可以認為數值模型和其參數是可靠的。

由于煤巖存在應變硬化特性，采用一般的彈性或者彈塑性材料模型無法有效模擬，工程上多采用JH砼材料(Johnsin-Holmquist-Concrete)來近似模擬巖石材料，其實質就是HJC模型，并在原有19個物理參數的基礎上又引入了2個軟件參數，實現了模型的無量綱化。研究表明[16-17]，HJC模型主要對其硬化參數A、B、N和靜態試驗參數(抗壓強度，抗拉強度，密度)敏感，壓力參數μc、μl以及pc、pl也對模型有一定的影響，其余參數對模型的影響均小于5%。靜力學參數可以由試驗直接獲取，易于確定；而各壓力參數也均有明確的物理意義，可以按文獻[16]提供的方法確定。準確地確定硬化參數A、B、N是建立HJC材料模型的關鍵，理論上可以通過材料屈服面方程計算確定，但由于煤巖材料大多存在內部缺陷和初始損傷，即便進行大量實驗，也難以獲得準確的屈服面，且不同區域的煤巖屈服面不同，不具備可推廣性，實際工程意義不大。本文通過數值模擬和試驗比對反演的方式近似確定上述參數，該方法對試驗要求低，且簡單易行，便于工程應用，但在比對反演過程中試算是不可避免的。

2.2 數值模型的建立

本次試驗使用的分離式霍普金森壓桿試驗裝置，子彈長為30 cm，入射桿和透射桿長分別為3.1 m和2.5 m，所用材料為低合金鋼，彈性模量210 GPa，泊松比0.25，試樣厚度為25 mm。采用Solid164實體建立模型，桿件和試樣分別采用2 mm和1 mm的映射Lagrange網格劃分，通過接觸算法模擬撞擊，為面與面自動接觸，整個模型共有單元1 621 225個，其中試樣單元數為49 725，節點1 749 538個，整體模型如圖4所示，模型中不考慮吸收桿和能量回收裝置的作用。

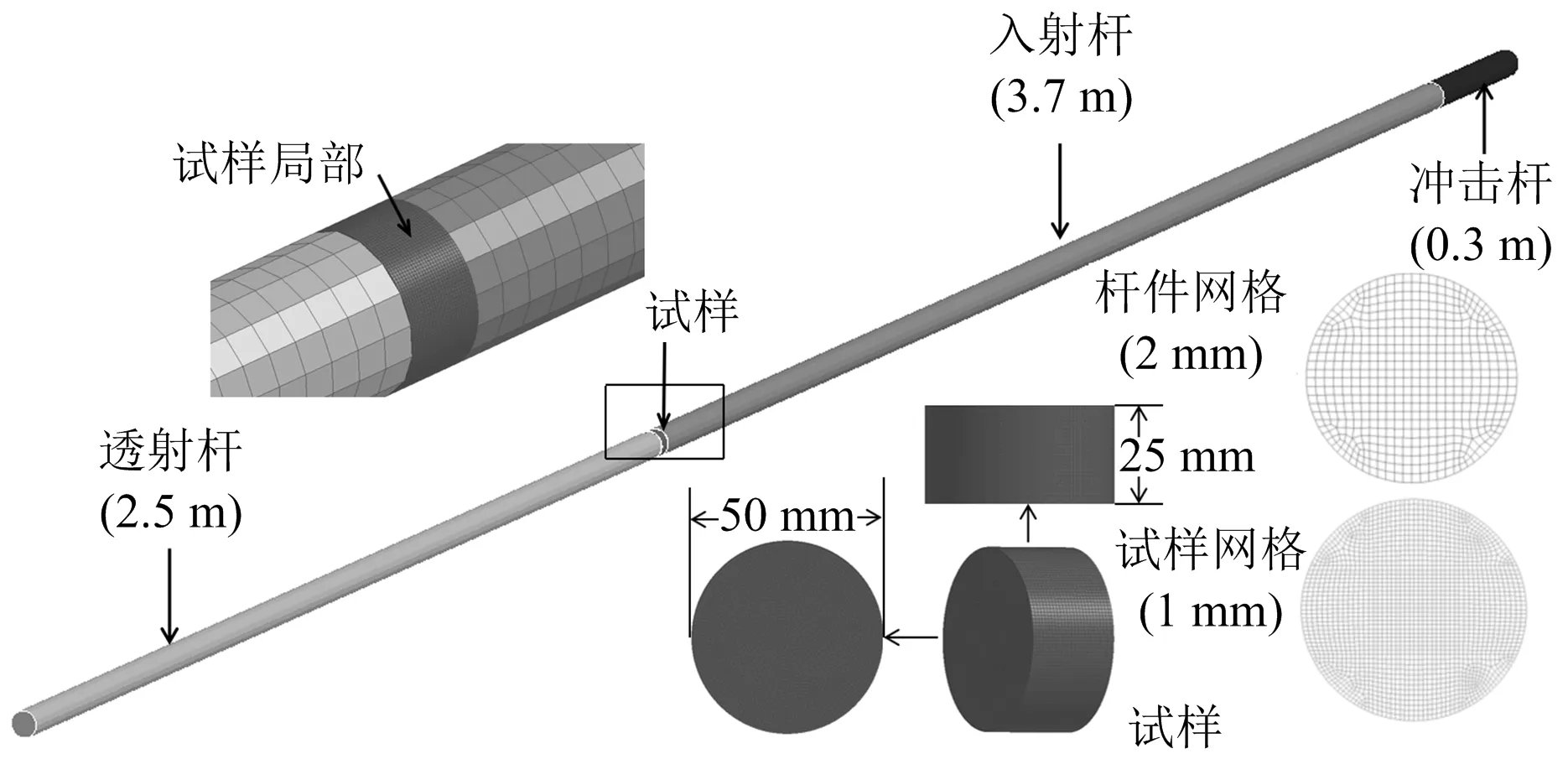
圖4 SHPB數值模型

2.3 模型參數的確定

首先通過調整參數試算，使數值模擬的應變信號與試驗實測的應變信號盡量接近，當兩者的整體趨勢和峰值大小相吻合時就可以得到模型參數的預測值。如果采用預測值模擬的應變信號能同時與多組試驗值相吻合，則說明預測值具備推廣性，就可以選取該參數為模型參數。將數值試驗也分為3組，分別賦予子彈3.54、5.88、8.13 m/s的初始速度，選取入射桿距離試件65 cm和透射桿距離試件40 cm處的微元，讀取其應變時程曲線，與試驗實測值進行對比，當硬化參數A、B、N分別取值0.76、1.66、0.72時，第1組數值模擬的應變時程曲線都能與試驗實測值近似吻合。入射波(反射波)信號和透射波信號如圖5所示。該參數模擬的信號在沖擊速度為5.88 m/s和8.13 m/s時也能與試驗值較好的吻合。由數值模擬信號反演的本構曲線和試驗實測信號處理的本構曲線如圖6所示，兩者較為吻合。

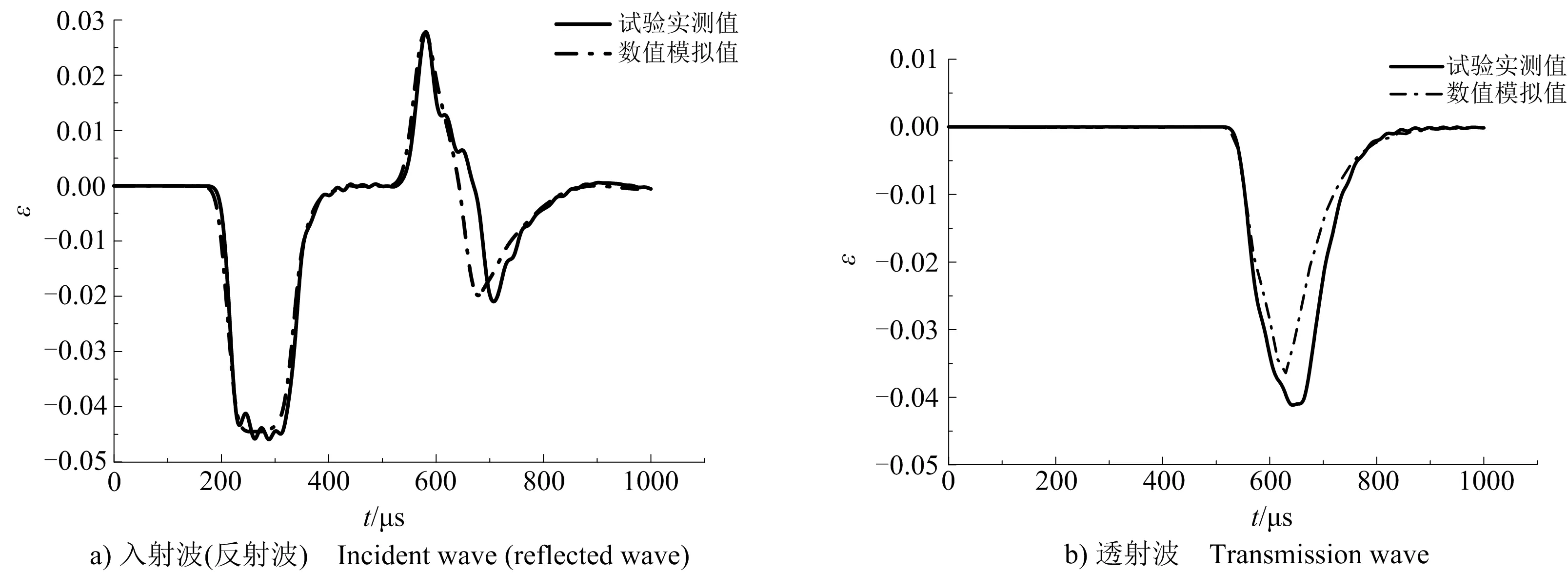
圖5 第1組應變信號數值模擬值與試驗實測值對比

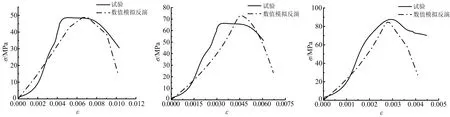
圖6 應力-應變試驗曲線與相應數值模擬反演曲線對比

綜上所述，可以近似確定煤巖HJC模型參數如表1所示。

表1 煤巖體HJC模型參數

3 煤巖動態破碎特性模擬

通過添加失效條件能夠直觀地模擬巖石的脆性破壞過程，在ANSYS/LS-DYNA中可以通過添加關鍵字MAT_ADD_EROSION實現。根據試驗，沖擊作用下煤巖在峰后才出現破壞，不能夠通過壓應力來定義失效；同樣的，在不同加載速率下的破壞壓應變有明顯差異，也不能通過壓應變定義失效。圖1中，沖擊破壞的煤巖斷面粗糙，是典型的張拉斷面，根據巖土塑性力學的觀點，巖石材料的破壞面包括應力狀態極限面和體積極限面，那么可以采用最大拉應力和最大體積應變來共同定義破壞條件。

3.1 煤巖破碎狀態的模擬

數值模型最終的破壞狀態如圖7所示，試樣單元共15層，每層3 315個單元，共計49 725個單元，括號內為增設失效條件后，試樣模型中未破壞單元數和損傷單元占總單元的比例。

圖7 試樣模型及中間截面的最終破壞形態

結合圖6和圖7可知，隨著應變率的增加，在加載段煤巖的壓密段呈減小趨勢，彈性段出現明顯的加強，應力增長效果明顯，說明應變率強化效應明顯，同時在峰后階段及卸載段，煤巖的峰值應變和極限應變都出現了應變強化效應，致使峰值變化加劇，峰值應變減小，極限應變降幅明顯，說明隨應變率的提高煤巖的脆性特性加強。

煤巖在沖擊下的破壞，一般伴隨有裂紋的出現、延伸擴展和貫通，但在數值模擬中由于微元的尺度較大(mm數量級)，且未考慮初始缺陷和不均勻性，所以難以模擬該過程，低速沖擊下多數模型破碎成蜂窩狀，與實際破壞差異較大。如果從斷裂力學和能量平衡的角度分析，產生較大的碎塊時的耗能要遠小于產生較小的碎塊。可以近似的認為沖擊輸入的能量僅消耗于產生尺寸較小的碎塊，即將體積較大的碎塊等價于模型中保留的部分微元，那么數值模型與試樣的實際破碎狀態存在一定的相似性，隨著沖擊速度的增大，最終破碎形式嚴重，存在更多的細小碎塊。這種相似性也在一定程度上驗證了材料模型的可靠性。

3.2 煤巖損傷演化的模擬

由于煤巖沖擊破壞是在極短的時間內完成的，即便采用高速攝像設備，也無法清晰的觀測沖擊破壞的過程，更無法了解巖石內部的破壞過程。通過假設失效條件，數值試驗手段可以完整而清晰地重現該過程。本文選取第1組數值模擬在630 μs(出現表面損傷)、720 μs(損傷快速增加)和870 μs(損傷基本完成)3個典型時刻的狀態進行分析對比，從軟件導出的試樣剖面如圖8所示。

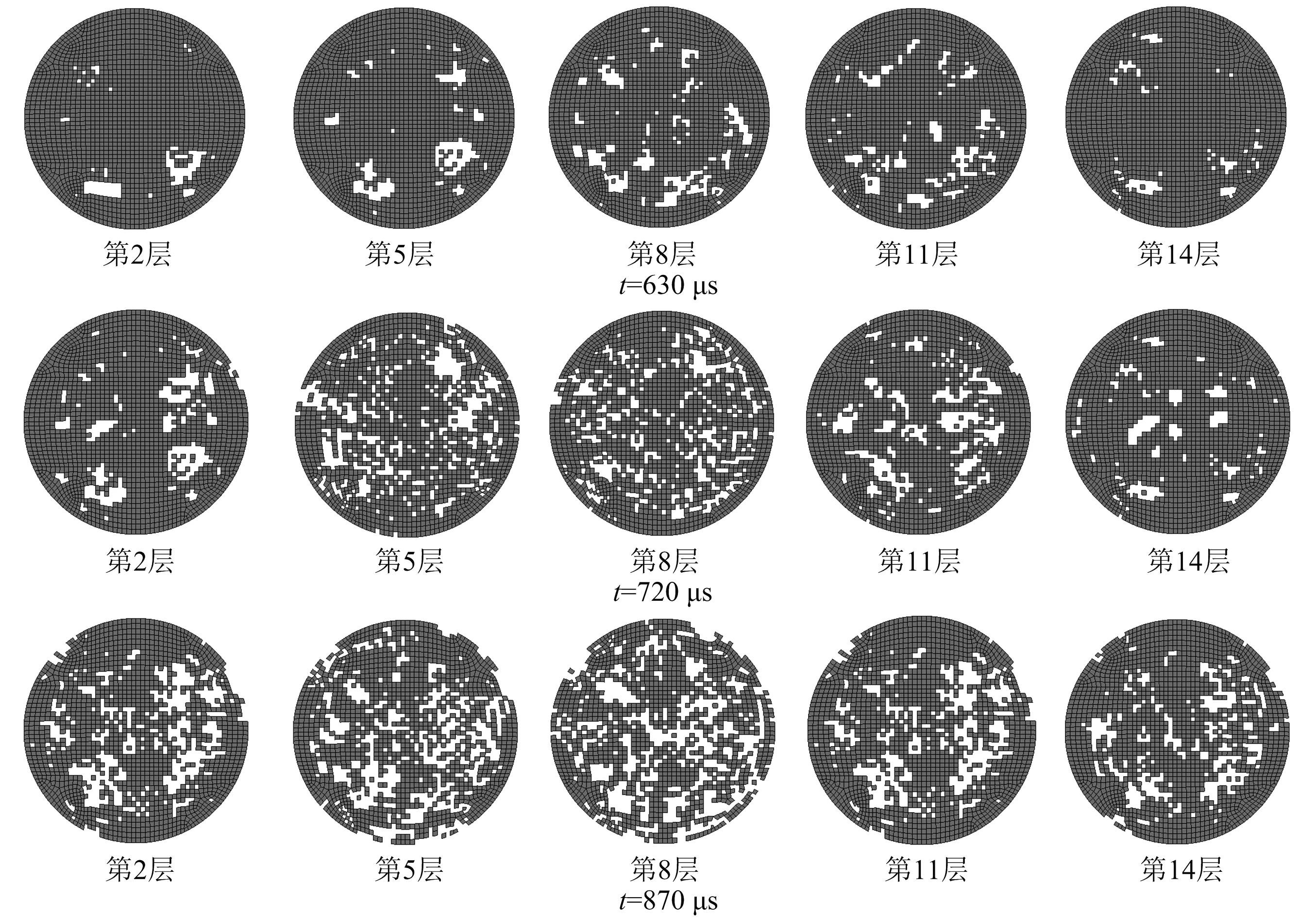
圖8 第1組數值模擬試樣不同時刻不同層模擬的損傷狀態

根據圖8分析認為，隨著壓縮波的加載，表面微元基本處于受壓狀態，其破壞原因主要為應變過大，而內部單元由于變形受到周邊微元的約束，應變較小，但容易出現局部受拉現象，少量微元因拉應力達到限值而率先破壞。當某微元破壞后，其周邊微元受到的約束消失形成自由表面，使得應變增大，最終破壞，出現了損傷集聚現象。

隨著壓縮波的加強，整體損傷程度明顯增大，損傷分布趨向均勻。在壓縮波峰值通過試件前，試件整體為受壓狀態，損傷發展相對緩慢，隨著峰值的通過，試件的受壓區域開始減小，出現大量受拉區，大量微元出現受拉破壞，這一階段損傷發展較峰前段迅速。隨著壓縮波的進一步減弱，試樣內部拉應力減小，損傷過程基本結束。

加載段煤巖在壓縮和拉伸應力波作用下，試樣形成多條主貫通裂隙用于抵抗變形，使得煤巖達到峰值應力，而在卸載段煤巖的整體結構遭到破壞無法繼續維持原有形態，試樣主裂隙周邊微裂隙擴展，損傷加劇，最終沿主裂隙發生失穩破壞，因此煤巖的卸載段損傷較加載段損傷更為嚴重。

比較同一時刻不同層的損傷程度，中間層微元的損傷比例明顯高于周邊層，這說明煤巖內部受到的沖擊損傷的更加嚴重，這與內部微元相互作用產生的復雜應力狀態有關。

需要說明的是，本文的數值試驗是基于假設的失效準則得到的，具有很大的局限性，楊更社等[23]、葛修潤等[24]基于CT檢測技術研究煤巖受靜載損傷時也發現過許多與本文數值模擬相類似的現象，但由于試驗設備和技術手段的限制，無法實現沖擊過程的CT即時掃描，數值試驗的結論還有待進一步驗證，但數值試驗反演的思想對于后續研究有一定的啟發作用。

4 結論

1)煤巖在沖擊作用下表現出和靜載下完全不同的力學特性，其抗壓強度和彈性模量隨著加載應變率的增加都有顯著的提高，尤其出現明顯的應變硬化特性。

2)HJC模型是一種合理的煤巖材料動態模型，可以較好的描述煤巖在單軸沖擊作用下的本構關系，通過基礎力學試驗和少量沖擊試驗，借助數值試驗手段就能快速確定模型的主要參數。

3)通過ANSYS/LS-DYNA模擬了煤巖沖擊破壞的過程，隨著沖擊速度的增加，損傷微元比例越高，微元聚集體越少，破碎程度越嚴重，整體趨勢與試驗結果一致。

4)通過假設失效準則的數值試驗手段，研究了煤巖沖擊破壞的損傷演化過程，發現煤巖的卸載段損傷較加載段損傷更為嚴重，試件內部損傷比表面嚴重。