基于邊坡穩定性的爆破振動控制標準確定方法

吳新霞，饒 宇,2，胡英國，柴朝政

(1.長江科學院水利部巖土力學與工程重點實驗室，武漢 430010；2.武漢理工大學土木工程與建筑學院，武漢 430070；3.中國三峽建設管理有限公司，成都 610000)

爆破振動控制標準應根據爆破振動荷載特征和保護物自身特點進行確定。由于保護物類型眾多、同類保護物特征往往存在很大差別，現有的規范規程往往難以做到面面俱到，如何從保護物自身的特點確定爆破振動控制標準對工程安全至關重要。盧文波等[1]、羅憶等[2]認為確定爆破振動控制標準要考慮結構振動特性、破壞機理、動力穩定以及作用時間等因素；在具體實施過程中，孫金山等[3]從邊坡不發生剪切和張拉破壞的角度確定了不同級別巖體的爆破振動安全控制標準；吳新霞等[4]根據受力分析，結合抗震烈度和工程類比確定了圍堰拆除各類保護物的爆破振動安全控制標準；劉美山等[5]結合爆破振動衰減規律、聲波測試驗證以及工程類比等方法確定了高邊坡的爆破安全控制標準。胡英國等[6]從應力波衰減的角度提出了高邊坡爆破安全控制標準的數學表達式。

邊坡爆破振動安全控制應該包含兩方面的內容，其一是近區保護物的損傷控制，例如控制爆破對保留巖體(建基面)的損傷深度，這是局部的損傷控制，這種損傷的爆破振動控制標準當前研究較為深入。其二是爆破振動對邊坡整體穩定性的影響，這是整體的穩定控制。陳明等[7-8]提出了等效加速度的概念，并以此來計算邊坡爆破動態穩定性；馬沖等[9]基于數值模擬的結果，采用強度折減方法確定了含軟弱夾層邊坡穩定的爆破安全判據；余海兵等[10]結合擬靜力法、應力判別法和數值模擬等方法確定了含軟弱層邊坡振速安全閥值。

從邊坡的穩定性的角度確定爆破振動控制標準對工程安全具有重要的意義，但現有的研究和規范規程在確定爆破振動控制標準時對邊坡穩定性的考慮偏少，邊坡穩定性與爆破振動速度之間的關系難以定量分析。筆者從理論分析上提出了基于邊坡穩定性的爆破振動控制標準確定方法，探討了爆破振動安全控制標準與邊坡強度參數的關系，并將相關方法運用到工程實踐中，為邊坡爆破安全控制提供了新的思路。

1 控制標準確定方法

1.1 滑塊穩定性分析

巖質邊坡穩定性主要由其結構面控制，以單斜貫穿型結構面沿坡底切腳出露這一代表性邊坡進行分析，取代表性斷面將三維邊坡作為平面應變問題考慮。滑塊力學分析模型如圖1所示。

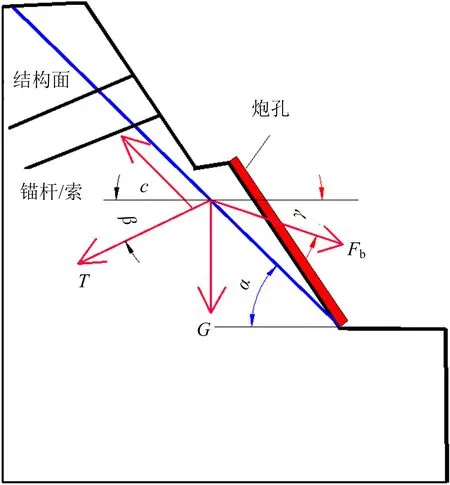
圖1 滑塊力學分析模型

滑動面上抗滑力FR和下滑力FT分別為

FR=[Gcosα+Tsin (α+β)-Fbsin (α-γ)]tanφ+cL+Tcos (α+β)

(1)

FT=Gsinα+Fbcos (α-γ)

(2)

式中：G、T、Fb分別為重力、錨固力和爆破作用力，N；φ、α、β、γ分別為結構面內摩擦角和結構面、錨固力、爆破作用力與水平面的夾角，°；c為結構面黏聚力，Pa；L為滑面長度，m。

1.2 振動控制標準的確定方法

對于爆破荷載作用下的邊坡穩定性，爆破作用力作用于滑塊重心位置，爆破作用力Fb表示為[11]

(3)

式中：b0為動力折減系數，一般取0.1～0.3，部分學者認為b0為0.008～0.152[12]；m為滑塊質量，kg；a、g分別為爆破加速度和重力加速度，m/s2。

爆破振動符合正弦函數特征，其加速度值a=2πfv，f為振動頻率，v為質點振動速度。則爆破荷載可以表示為

(4)

當Fb=0，滑塊處于靜力狀態：

Kj=

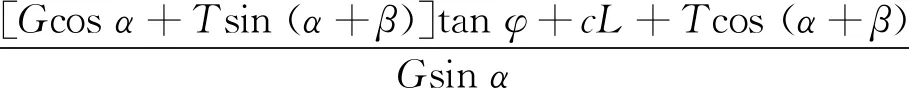
(5)

式中：下標j表示靜力狀態，其他參數含義同前。則：

(Kj-cotαtanφ)Gsinα=Pj

(6)

令Pj=Tsin (α+β)tanφ+cL+Tcos (α+β)。

當Fb≠0時，滑塊處于動力狀態，其動態穩定性安全系數[Kd]表示為

[Kd]={[Gcosα+Tdsin (α+β)-Fbsin (α-γ)]tanφ+cdL+Tdcos (α+β)}/[Gsinα+Fbcos (α-γ)]

(7)

式中：下標d表示動力狀態，其他參數與前文相同。同理也可以設定動態參數，則：

[Kd]=

(8)

其中Pd=Tdsin (α+β)tanφ+cdL+Tdcos (α+β)。

相關研究[13-14]和規范[15]認為動態強度參數一般比靜態強度參數提高20%，對于高頻的爆破荷載更是如此，則Pd=1.2Pj，根據式(6)和式(8)得：

(9)

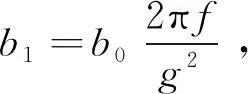
[Kd]=

(10)

以質點峰值振動速度作為爆破安全控制指標，也可以轉換為如下表達方式：

[PPV]=

{1.2Kj-([Kd]+0.2cotαtanφ)}×

(11)

式中:Kj為邊坡靜態穩定性安全系數；[PPV]為爆破振動安全控制標準，即質點允許峰值振動速度，cm/s；f為主振頻率；[Kd]為邊坡動態穩定性安全系數設計值，反映了邊坡抗爆破振動能力大小和對動力荷載控制的嚴格程度,[Kd]越大表明邊坡動力設防要求越嚴，不良地質條件巖體和強度參數受動力荷載影響較大的巖體，[Kd]越大，爆破振動安全控制標準數值越小。

對于某一邊坡，控制性滑動面傾角和內摩擦角一定，爆破孔網參數相對固定，則邊坡的動態穩定主要與邊坡靜力狀態下的安全系數和質點爆破振動速度有關。但并不是邊坡靜態穩定性安全系數越大就一定能承受越大的爆破質點振動速度，還與動態穩定性安全系數設計值有關，現實中存在靜態穩定性安全系數較大的邊坡在較小振動下破壞的情況。

2 工程案例

以我國某百萬千瓦級水電站為例，其拱肩槽邊坡斷層、擠壓帶和裂隙發育，特別是大型斷層貫穿拱肩邊坡(見圖2)，對邊坡穩定極為不利。貫穿斷層參數為：tanφ=0.45，斷層傾角55°～60°，黏聚力c=0.08 MPa。在開挖過程中，斷層出現顯著的卸荷變形，擬通過對現有邊坡進行加固后實施爆破開挖，而如何確定加固初期的爆破振動控制標準是需要解決的難題。

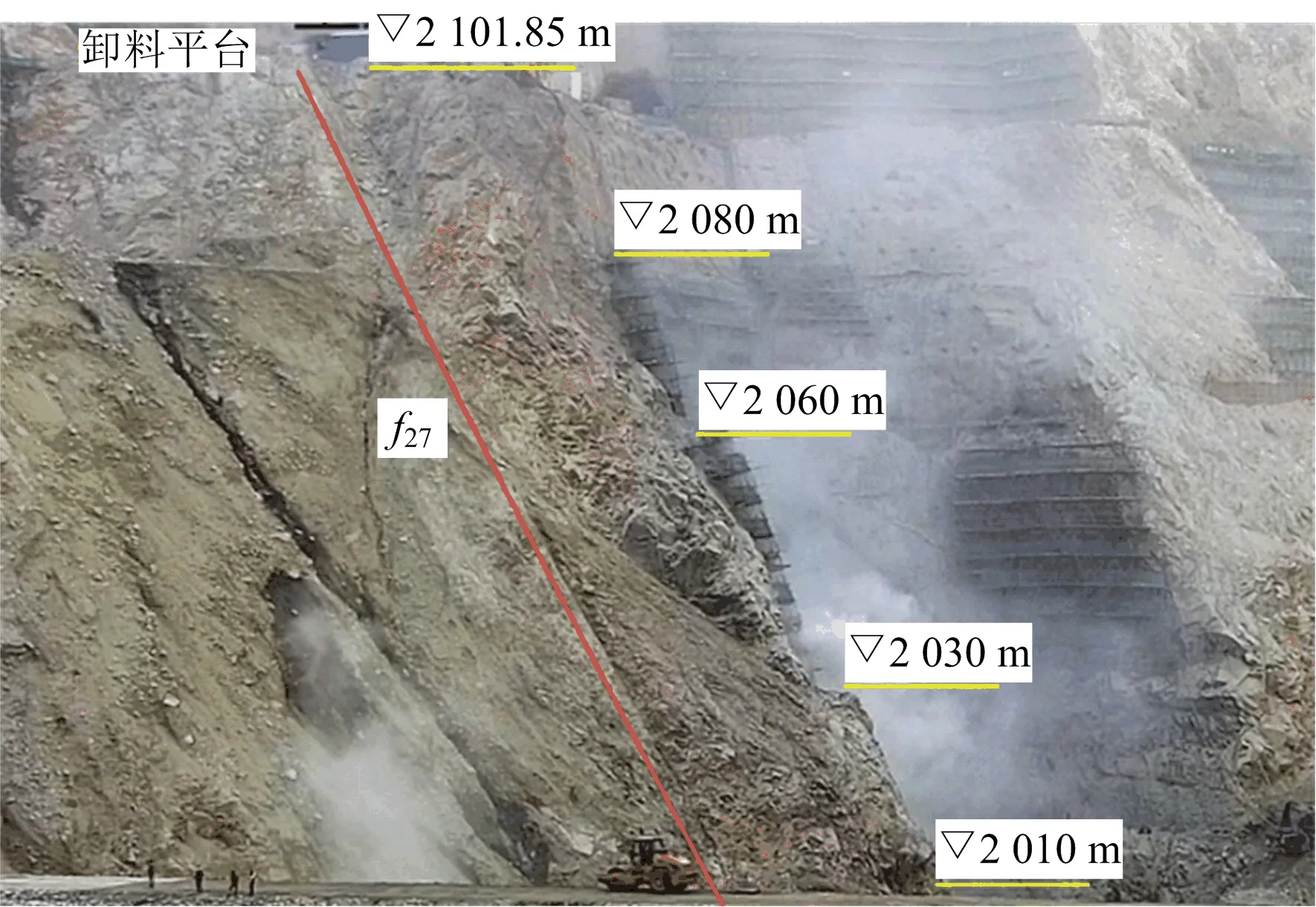
圖2 拱肩槽邊坡

拱肩槽邊坡為A類(樞紐工程區)Ⅰ級邊坡，邊坡設計安全系數如表1所示[16]。

表1 拱肩槽邊坡設計安全系數

2.1 方法的應用

短暫工況指的是施工期遭遇短期外部環境變化時的設計安全系數，符合爆破開挖的情況。因此，靜態穩定性安全系數達到1.2的邊坡能夠承受爆破質點振動速度為10 cm/s(一般邊坡爆破振動安全控制標準)。考慮邊坡處于靜力穩定臨界狀態，邊坡靜態穩定性安全系數為1.00，此時邊坡剛好是不能承受振動，即爆破振動安全控制標準為0 cm/s。

臨界狀態：Kj=1，不能受振，[PPV]=0 cm/s，則：

0.2cotαtanφ=1.2-[Kd]

(12)

需滿足[Kd]≥1.2-0.2cotαtanφ=1.14，否則，出現邊坡失穩卻能受振的情況，[Kd]越大對振動控制越嚴。

當Kj=1.2時，[PPV]=10 cm/s，則：

[Kd]=

(13)

在邊坡地質條件和爆破參數無顯著變化下，邊坡[Kd]可看做一個定量，則通過式(11)和(13)可得：

[PPV]=0.1×

(14)

為使式(14)有意義，[Kd]≤1.44-0.2cotαtanφ=1.38，Kj為加固后的邊坡靜態穩定性安全系數，爆破振動安全控制標準與邊坡靜態穩定性安全系數、動態穩定性安全系數設計值、斷層傾角、黏聚力和內摩擦角相關。

靜態穩定性安全系數Kj與斷層傾角和內摩擦角、錨固力及錨桿/索傾角以及滑塊質量等有關，與[PPV]并非簡單的線性關系。其中，α與[PPV]呈負相關關系，φ與[PPV]呈正相關關系，Kj總體上與[PPV]呈正相關關系。

不考慮爆破對巖體的損傷，在不計錨固力的情況下，根據工程案例參數，僅從穩定性角度表明[PPV]與相關參數的變化關系如圖3～圖5所示。

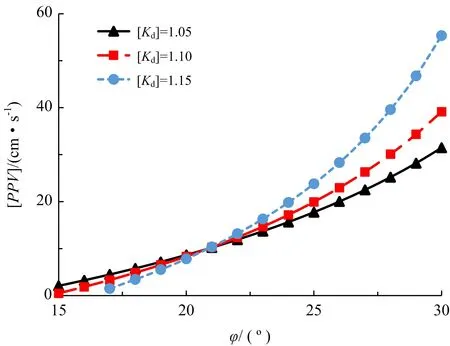
圖3 [PPV]與內摩擦角的關系

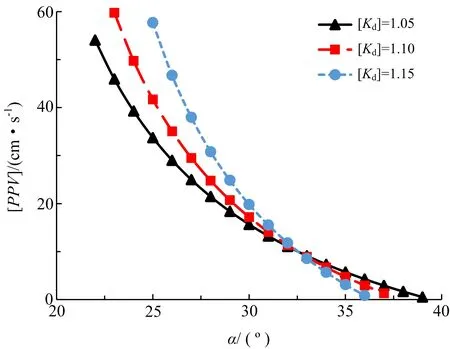
圖4 [PPV]與滑動面傾角的關系

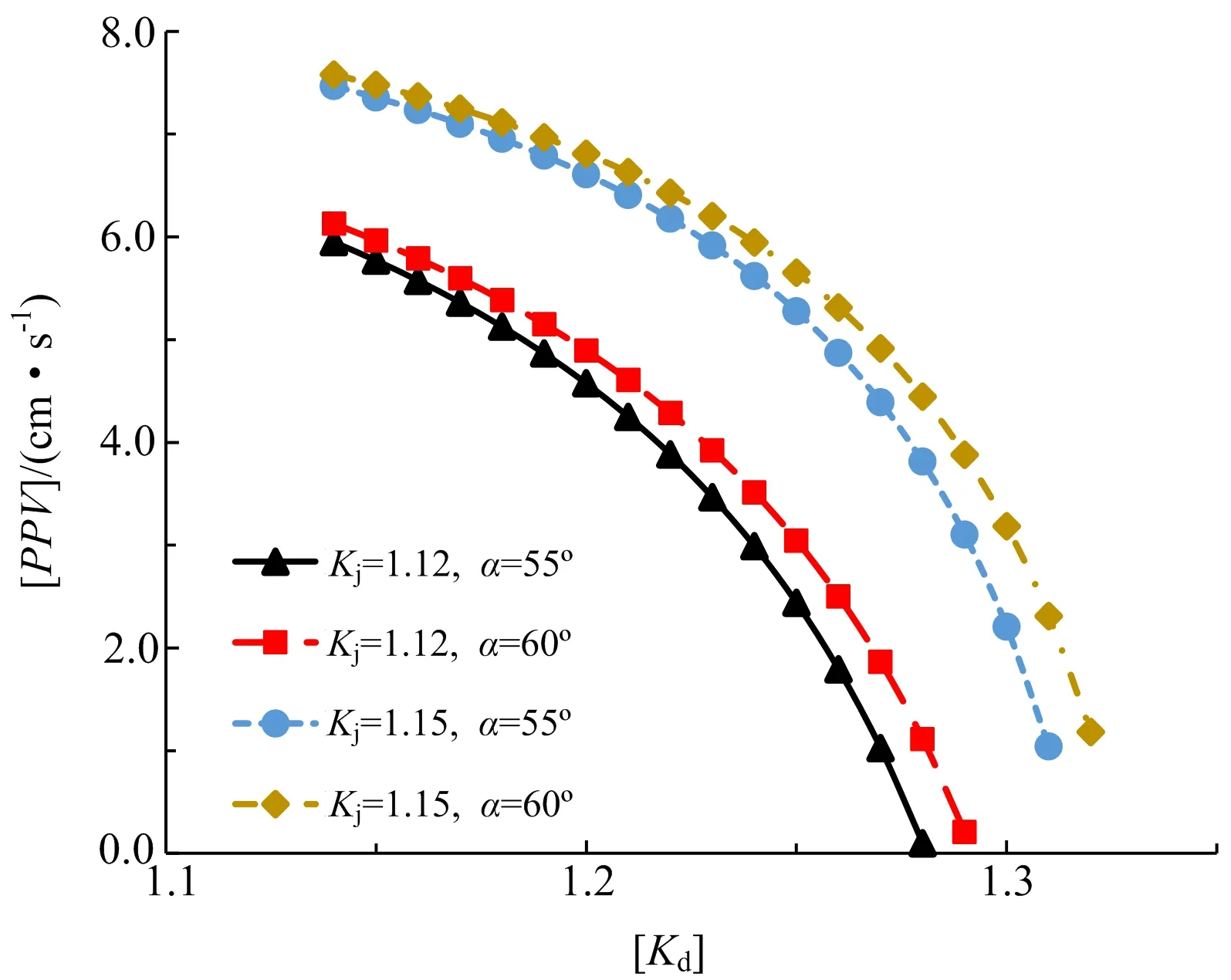
圖5 [PPV]與[Kd]的關系

由圖3～圖5可知，爆破振動安全控制標準[PPV]與滑動面內摩擦角呈現正相關關系，隨內摩擦角增大，[PPV]迅速增大，且增大速率越來越快；而[PPV]與滑動面傾角和動態穩定性安全系數設計值[Kd]呈現負相關關系，一定范圍內，隨傾角增大，[PPV]值降低速率逐漸變慢；而隨[Kd]增大，[PPV]降低速率卻越快； [Kd]越大，表明邊坡對振動控制要求越嚴，[PPV]越小。

圖3～圖5僅為了表明相關的變化規律，具體數值與多個參數相關，準確數值需要根據工程實際情況進行計算。

特別需要說明的，當Kj=1～1.3時，既要考慮爆破對巖體的損傷，也要考慮爆破對邊坡穩定性的影響。當Kj<1時，即完全不能受振，靜力狀態下邊坡即已經失穩；當Kj>1.3時，從邊坡穩定的角度質點振動速度v可以大于10 cm/s，但需要考慮爆破對巖體的損傷，仍按照相關規范進行控制。

2.2 爆破振動安全控制標準的確定

根據前期的地質調查，確定了二維不利塊體4個(KT1～ KT4)，三維不利塊體8個(ZKT1～ ZKT8)，并獲得了現狀、加固后和參數反演等3種工況下的邊坡靜態穩定性安全系數，其中，參數反演工況指的是以現狀為臨界狀態(Kj=1)反演出結構面參數并計算加固后的安全系數。采用式(14)計算關鍵塊體的爆破振動安全控制標準如表2～表4所示，為了說明情況，Kj>1.3時的控制標準也通過式(14)計算列出，但實際上，從控制損傷的角度控制標準不宜大于10 cm/s。

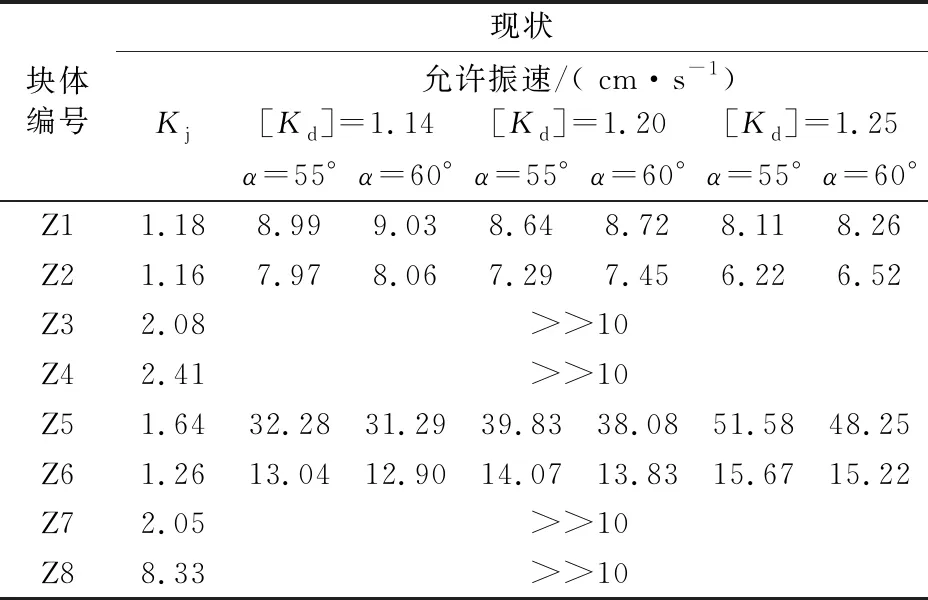
表2 基于三維塊體穩定性分析的爆破振動安全控制標準

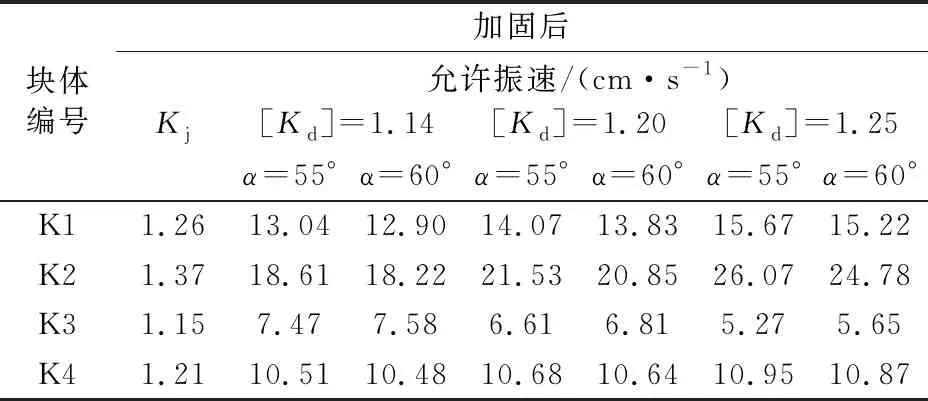
表3 基于二維塊體穩定性分析的爆破振動安全控制標準

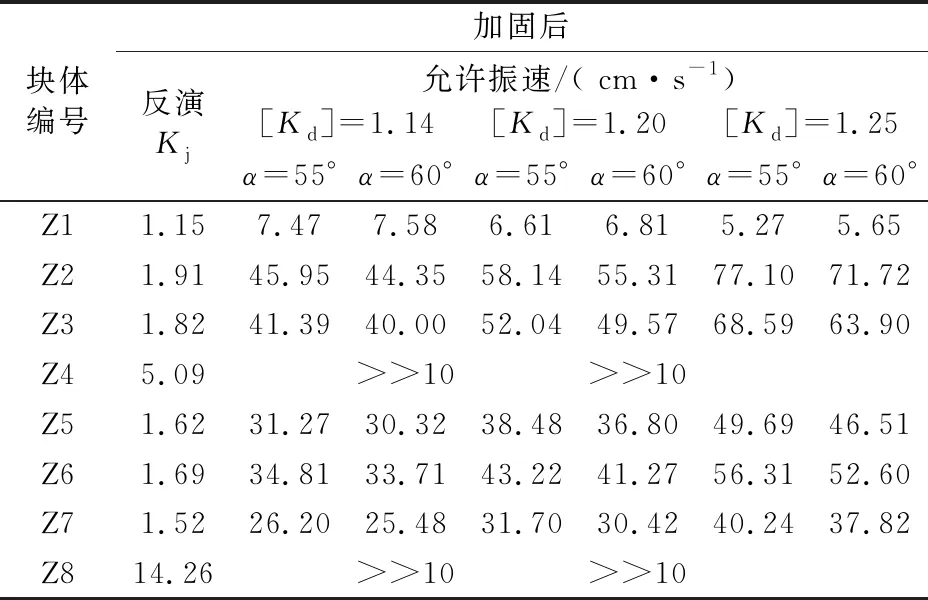
表4 基于參數反演的三維塊體穩定性分析的爆破振動安全控制標準

根據上述計算可知，考慮到拱肩槽邊坡地質條件復雜，在加固初期，通過設置較大的[Kd]對邊坡爆破開挖作業進行嚴格控制，對于巖體質量差的部位，[Kd]宜比臨界值1.14大5%～10%，則確定5.27 cm/s的質點峰值振動速度控制標準能夠滿足邊坡動態穩定性要求，實際實施過程中控制點為上一級馬道坡腳，因此還具有一定的安全富裕。后期待支護完成、邊坡變形穩定，可以根據工程實際適當放寬控制要求。

從后期實施效果來看，通過采取加固和控制爆破等措施，斷層多點位移計監測結果顯示日位移增量從之前的最大值1.15 mm/d、平均日增量0.71 mm/d，減小到實施初期最大1 mm以內、80.95%測次增量在0.5 mm以內、平均日增量0.25 mm/d，平均位移日增量減小了65%，后期邊坡變形穩定，開挖質量優良(見圖6)，爆破取得了成功。

圖6 拱肩槽邊坡爆破效果

3 討論

3.1 爆破振動安全控制標準極小值

根據式(11)，當邊坡靜態穩定性安全系數和動態穩定性安全系數設計值取為一定值時，函數f(γ)=sin (α-γ)tanφ+[Kd]cos (α-γ)存在極大值，[PPV]取極小值，即當爆破作用力與斷層夾角γ=α-arctan(tanφ/[Kd])時，[PPV]取得極小值。此時爆破荷載作用角度可稱之為最不利角。

例如，當[Kd]=1.3、tanφ=0.45時，[PPV]極小值[PPV]min為

[PPV]min=

(15)

γ=40.9°為最不利角，邊坡穩定性最差。

3.2 爆破作用角度

爆破作用力與滑動面夾角變化較大，當將爆破作用當作平面問題不考慮切向爆破振動速度(與邊坡走向一致)時，根據同一時刻質點振動速度比值(垂直向/水平徑向)可大體推算爆破作用角度。因為速度存在正負方向，爆破作用方向在4個象限均可能出現，最不利情況還是如圖1所示的斜向右下，既增大了下滑力又降低了抗滑力。僅考慮最不利情況，通過對監測質點峰值振動時刻的速度比值進行統計，可大體獲得最大爆破力作用角度。開挖施工期爆破作用力與滑動面夾角(α-γ)統計(共125點·次)如表5所示。

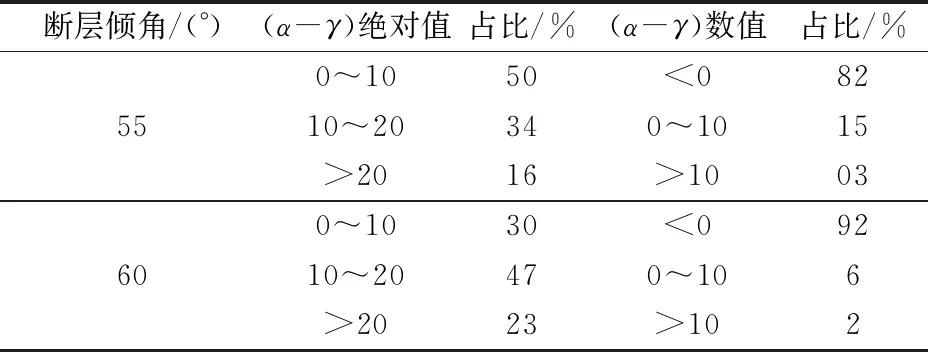
表5 爆破作用力與滑動面夾角(α-γ)統計

根據統計可知，大多數情況下(>80%)最大爆破力作用方向并非位于最不利方位，更多的是偏向巖體內部，而(α-γ)絕對值在20°以內的情況占比為77%～84%。

4 結論

1)提出了基于滑塊穩定性分析的邊坡爆破振動控制標準的確定方法，爆破振動安全控制標準[PPV]與邊坡靜態穩定性安全系數Kj、動態穩定性安全系數設計值[Kd]和滑動面傾角、黏聚力和內摩擦角有關。

2)[PPV]與Kj和滑動面內摩擦角呈非線性正相關關系，并隨內摩擦角增大，[PPV]增大速率越快。

3)[PPV]與[Kd]和滑動面傾角呈非線性負相關關系，一定范圍內，隨[Kd]增大[PPV]降低越迅速，而隨傾角增大[PPV]降低越緩慢。

4)[Kd]反映了邊坡抗爆破振動能力大小和對動力荷載控制的嚴格程度，不良地質條件巖體和強度參數受動力荷載影響較大的巖體，[Kd]越大，[PPV]越低。

5)監測數據表明，超過80%的情況下最大爆破力并非位于最不利方位，最大爆破力作用方向與滑動面夾角小于20°的情況占比為77%～84%。

需要注意的是，具體的爆破振動安全控制標準需要根據工程實際情況進行計算得到，本文提出的確定方法是從邊坡穩定角度出發的，實際應用中還需要考慮爆破對保留巖體的損傷進行綜合確定。