Taylor-Couette流動特性與減阻實驗研究進展

張文云, 胡海豹, 文 俊, 曹 剛, 任劉珍

西北工業大學 航海學院, 西安 710072

0 引 言

隨著能源消耗的快速增加，能源問題已經成為全球性的問題。如何實現節能降耗是目前國內外關注的重要研究課題。研究表明，船舶航行時，其表面的摩擦力可占總阻力的70%～80%，即使在高速航行情況下，也可占到大約40%[1]。海洋運輸成本低廉，一直是國際物流的主要運輸方式，減少船舶航行阻力可節約能源，緩解由能源快速消耗造成的能源危機，對海洋開發向深海、遠海發展有重要意義。

間隙中充滿流體的同軸轉子可類比為流體力學中的經典Taylor-Couette流動模型。該模型具有結構簡單、便于開展高精度實驗測試等特點[2]，常與Rayleigh-Bénard(RB)對流模型和管道流動模型[3-5]一起，用于研究不穩定性[6-7]、非線性動力學[8-9]和湍流[10-13]等經典流體力學機理問題。同時，涉及Taylor-

Couette流動的軸類零件在工程中普遍存在，相關減阻研究不僅可以應用于工程領域，也可以推廣至其他流動。

研究Taylor-Couette流動的流動特性，對探索基于Taylor-Couette流動的減阻方法和減阻機理研究有重要的意義。本文系統介紹了Taylor-Couette流動的主要無量綱影響參數、流場結構與扭矩特性，總結了基于Taylor-Couette流動的減阻研究進展。

1 Taylor-Couette流動基本特征

1.1 Taylor-Couette流動的無量綱影響參數

Taylor-Couette流動模型由2個同軸旋轉的圓柱組成，圓柱間充滿流體，允許內、外圓柱以不同速度和旋向旋轉。圖1(a)為經典Taylor-Couette流動示意圖，旋轉圓柱間隙內一般存在成對、旋向相反的Taylor渦結構；圖1(b)為Taylor-Couette流動間隙軸向速度分布示意；圖1(c)為Taylor-Couette流動間隙方位角速度分布示意。影響Taylor-Couette流動的無量綱參數主要有雷諾數Re、泰勒數Ta及努塞爾數Nuω。

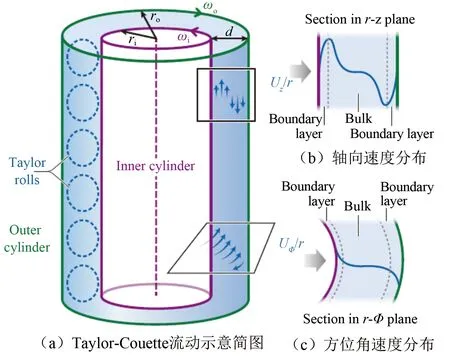
圖1 Taylor-Couette流動示意圖[2] Fig.1 The schematic diagram of Taylor-Couette flow[2]

內、外圓柱雷諾數Rei和Reo分別為：

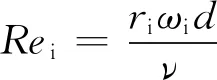
(1)

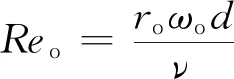
(2)

式中，ri、ro分別為內、外圓柱的半徑，ωi、ωo分別為內、外圓柱旋轉角速度，d為內外圓柱間隙，ν為流體運動黏性系數。一般定義Rei為正；當內、外圓柱旋向相同時，定義Reo為正；當外圓柱靜止時，定義Reo為零；當內、外圓柱旋向相反時，定義Reo為負。

為表征內、外圓柱半徑和曲率的影響，引入泰勒數Ta：

(3)

式中，η=ri/ro為內外圓柱半徑的比值。為表征內圓柱恒定角速度時所受的扭矩，Eckhardt等[14]定義了努塞爾數Nuω：

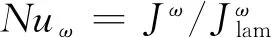
(4)

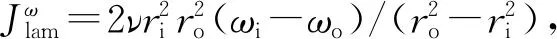
1.2 Taylor-Couette流動流場特性

1923年，Taylor[15]首次發現當內圓柱轉速ω超過臨界值ωc時圓柱間隙內流動會發生失穩，出現Taylor渦對。此后，學者們對Taylor-Couette流動的不穩定性和體系結構展開了廣泛的研究。1986年，Andereck等[16]系統總結了一定Rei和Reo范圍內Taylor-Couette流動的體系結構，如圖2所示。2014年，Ostilla-Mónico等[17]通過DNS方法模擬更高Ta下Taylor-Couette流動，進一步擴展了其體系結構，并給出了Taylor-Couette流動的終極狀態，如圖3所示。從圖中可見，Ta從7.04×105提升到4.63×109過程中，圓柱間隙流動會經歷層流狀態、過渡區和終極狀態(充分發展湍流狀態)。

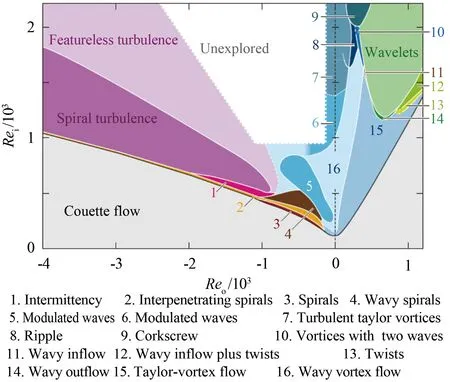
圖2 不同雷諾數條件下Taylor-Couette流動的流動體系[16]Fig.2 Flow regime of Taylor-Couette flow at different Reynolds numbers[16]

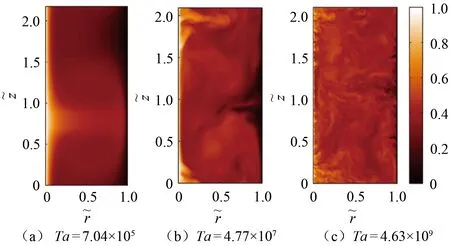
圖3 高泰勒數下Taylor-Couette流動瞬時速度場[17](η=0.714)Fig.3 Flow field of Taylor-Couette flow at high Taylor numbers[17]

Taylor渦結構和流動不穩定性不僅在同軸旋轉圓柱間隙流動中存在，在同軸圓錐面之間[18]、圓柱與圓錐之間[19]及同心橢球[20]之間也同樣會形成不同形態的Taylor渦和流動不穩定現象，如圖4所示。近年來，學者們還發現Taylor-Couette流動與對流[21-22]、黏彈性流體[23]、磁場[24]結合時，也存在有趣的流動不穩定性問題。

圖4 不同幾何結構下的Taylor渦的形態[18,20]Fig.4 Taylor vortex characteristic with different geometry structures[18,20]

1.3 Taylor-Couette流動的扭矩特性

Taylor-Couette流動的扭矩主要決定于Ta和內外圓柱半徑比η。Ostilla-Mónico等[25]通過實驗與數值模擬結合的方法，給出了不同半徑比η下扭矩(Nuω)與Ta之間的標度率關系，如圖5所示。在Taylor-Couette流動達到終極狀態之前，Nuω∝Taα，其中指數α依賴于內外圓柱半徑比η。當Taylor-Couette流動達到終極狀態時,α=0.38，即Nuω∝Ta0.38。這是因為在Taylor-Couette流動的終極狀態，不管是間隙的中心區域還是在邊界層區域，流動均變得非常紊亂。同時，Taylor-Couette流動中不同的流動狀態對應不同的標度率關系，當內外圓柱半徑比η=0.714時，標度率的主要規律如下：在外圓柱靜止、內圓柱轉動的狀態下，當邊界層和間隙區域均為層流時，α=0.33；當轉速繼續增加，間隙中的Taylor渦開始紊亂時，α<0.33，而在流動的終極狀態時，α>0.33。

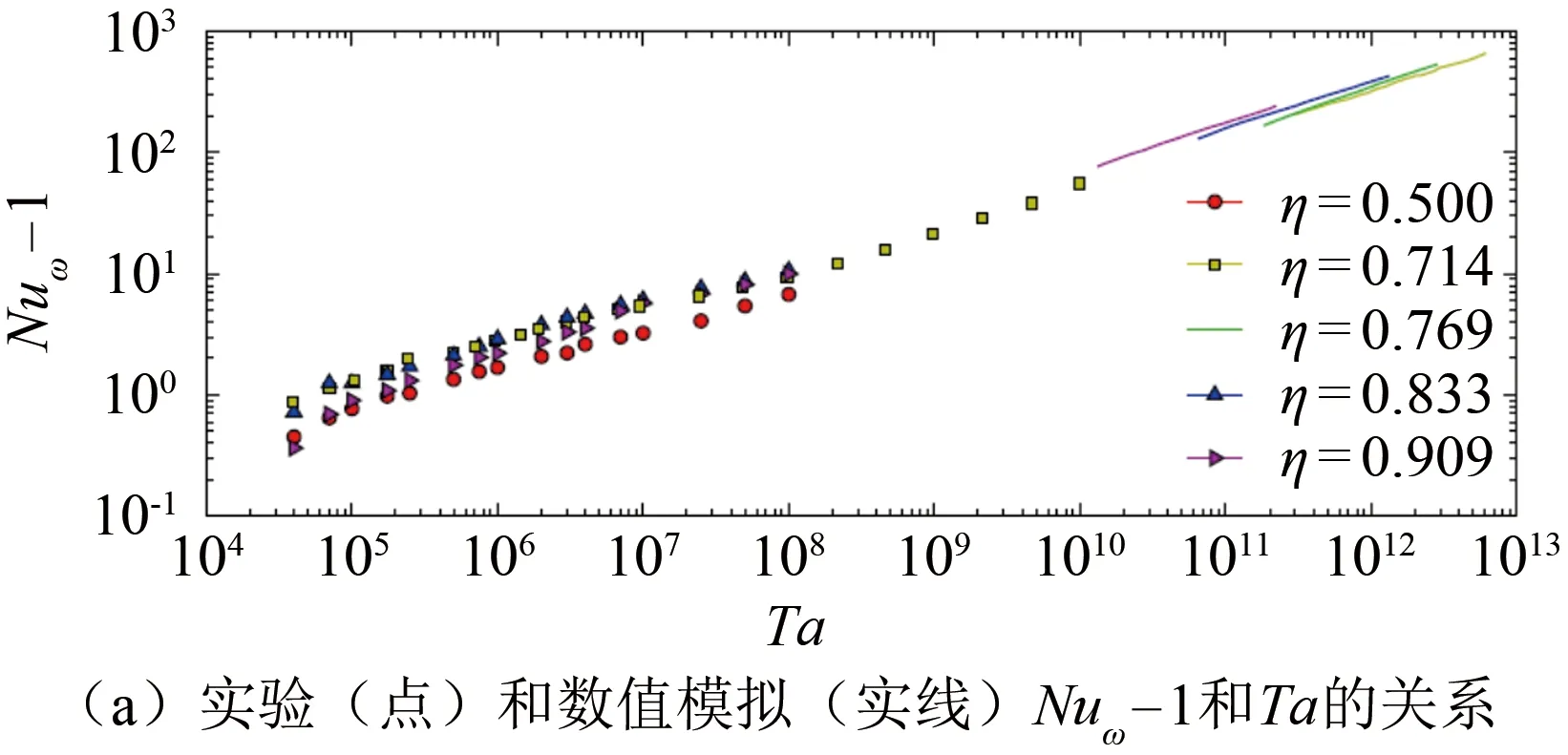
圖5 不同半徑比對扭矩的影響規律[25] Fig.5 Torque scaling with different radii ratios[25]

2 Taylor-Couette流動減阻研究

Taylor-Couette流動的阻力為摩擦阻力，因此各種減少摩擦阻力的方法(如氣泡減阻[26]、超疏水減阻[27]和溝槽減阻[28]等)都可用于減少Taylor-Couette流動內圓柱的扭矩。涉及減少摩擦阻力的減阻方法統稱為Taylor-Couette流動的通用減阻方法。Taylor-Couette流動的內外圓柱之間存在成對的Taylor渦結構,是內外圓柱間動量傳輸的主要途徑。設法降低Taylor渦引起的能量耗散，可以有效減小內圓柱的扭矩。通過減少Taylor渦對數和耗散的減阻方法統稱為Taylor-Couette流動的特有減阻方法。

2.1 通用減阻方法

1)氣泡減阻方法

Taylor-Couette流動中的氣泡受浮力、重力和離心力的共同作用，大多數氣泡會在內圓柱表面聚集分布，只有少部分氣泡會和Taylor渦相互作用，被卷入Taylor渦中[26]。Murai等[29]研究了在底部通氣時Taylor-Couette流動的扭矩特性和氣泡行為，實驗表明:通氣條件下Taylor渦的波長增加了32%，而內圓柱的扭矩下降了31%，如圖6(a)所示。Fokoua等[30]研究了不同雷諾數條件下氣泡尺寸對減阻效果的影響規律。大多數學者認為，氣泡減阻是由氣泡變形[31]或其對流動結構的影響[32]導致的，研究氣泡減阻機理對氣泡減阻實際應用具有非常重要的意義。Berg等[33]發現轉子表面粗糙時內圓柱的無量綱阻力明顯高于不通氣時，揭示了氣泡減阻是一個純邊界層效應。Gils等[34]發現氣體體積分數相同時減阻率隨雷諾數增高而變高，推導出氣泡變形量是影響氣泡減阻的一個重要因素。Verschoof等[35]在內外圓柱流體中加入表面活性劑，減阻率由40%降至4%，表明氣泡變形量對減阻效果有決定性作用。Bakhuis等[36]發現湍流時增加或減小剛性粒子尺寸會導致阻力輕微增加或減小。上述學者的研究揭示了氣泡減阻機理，為氣泡減阻的工程應用做出了貢獻。

2) 超疏水減阻方法

受荷葉表面憎水特性啟發，超疏水減阻作為新興的減阻方法受到學者們的廣泛關注。Srinivasan等[37]研究了湍流條件下超疏水表面的減阻特性，雷諾數為8×104時減阻率為22%，同時得到19 μm的有效滑移長度。Saranadhi等[38]加熱超疏水表面在相對低的溫度下形成穩定低溫Leidenfrost表面，最高實現約90%的減阻率，如圖6(b)所示。胡海豹等[39]通過在內圓柱表面構造親疏水相間環形條帶結構，得到超過70%的減阻率，如圖6(c)所示。Buren等[40]在圓柱表面加工凹槽，并在凹槽中填充烷烴，形成liquid-infused表面，實現約35%的減阻率，同時還發現減阻率隨黏性比、溝槽寬度、流體面積分數和雷諾數的增大而增大，如圖6(d)所示。

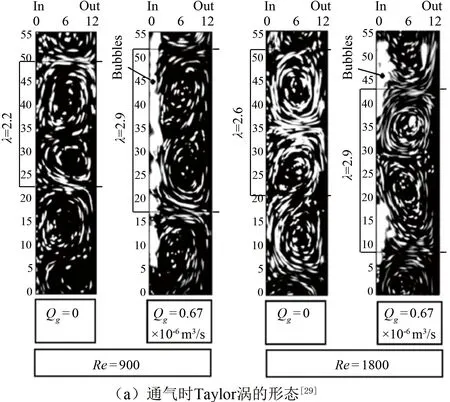
圖6 Taylor-Couette流動通用減阻方法Fig.6 Regular drag reduction of Taylor-Couette flow

3) 溝槽減阻方法

快速游動的鯊魚皮膚在流動方向上呈現溝槽結構，這些溝槽結構在湍流狀態下可減少皮膚摩擦阻力[41]。Greidanus等[42]在旋轉圓柱間隙流動的內圓柱表面構筑微米級溝槽，發現雷諾數小于4.7×104時，溝槽表面有更大摩擦系數；而當雷諾數大于4.7×104時，溝槽減阻開始顯現，并且雷諾數越大減阻效果越好。PIV測試表明，存在溝槽時內圓柱表面的速度梯度明顯減小。但是并不是所有尺寸的溝槽都能夠減少內圓柱的扭矩，Zhu等[43]發現內外圓柱表面構造的V型槽會誘導產生二次環流，導致內圓柱扭矩增大。Verschoof[44]和Zhu等[45]還發現在內圓柱外表面沿軸向布置矩形溝槽時均增大了內圓柱的扭矩。

2.2 Taylor-Couette流動特有減阻方法

1) 基于添加圓柱外筒的減阻方法

Grossmann等[46]推導了Rayleigh-Benard對流的耗散形式：

εd=εbulk+εBL

(5)

圖7 Taylor-Couette流動結構減阻方法[48] Fig.7 Structure drag reduction method of Taylor-Couette flow[48]

2) 基于Taylor渦調控的減阻方法

Mullin等[49]發現當液面高度變化時可維持不同對數的Taylor渦。Mansour等[50]做了相同的工作，研究了Taylor渦拉伸、壓縮時的穩定性限制，但未定量測試其減阻效果，如圖8(a)和(b)所示。Martínez-Arias等[51]進一步研究發現Taylor渦對數越多，內圓柱扭矩值越大。Brauckmann等[52]通過DNS模擬，也證實了Taylor渦對數與圓柱扭矩之間的這種關系，如圖8(c)和(d)所示。可見，維持較少的Taylor渦對數是旋轉圓柱間隙流動的潛在減阻方法。Xiao等[53]發現一定雷諾數范圍內，內圓柱旋轉加速度越大，Taylor渦對數越多。除了上述2種調控Taylor渦對數的方法外，胡海豹等還發現通過在內圓柱表面構筑氣環，不僅能降低Taylor渦強度，也能夠減少Taylor渦對數[39]；此外，Murai等[29]發現在旋轉圓柱間隙流動底部通氣時Taylor渦的波長也會增加。

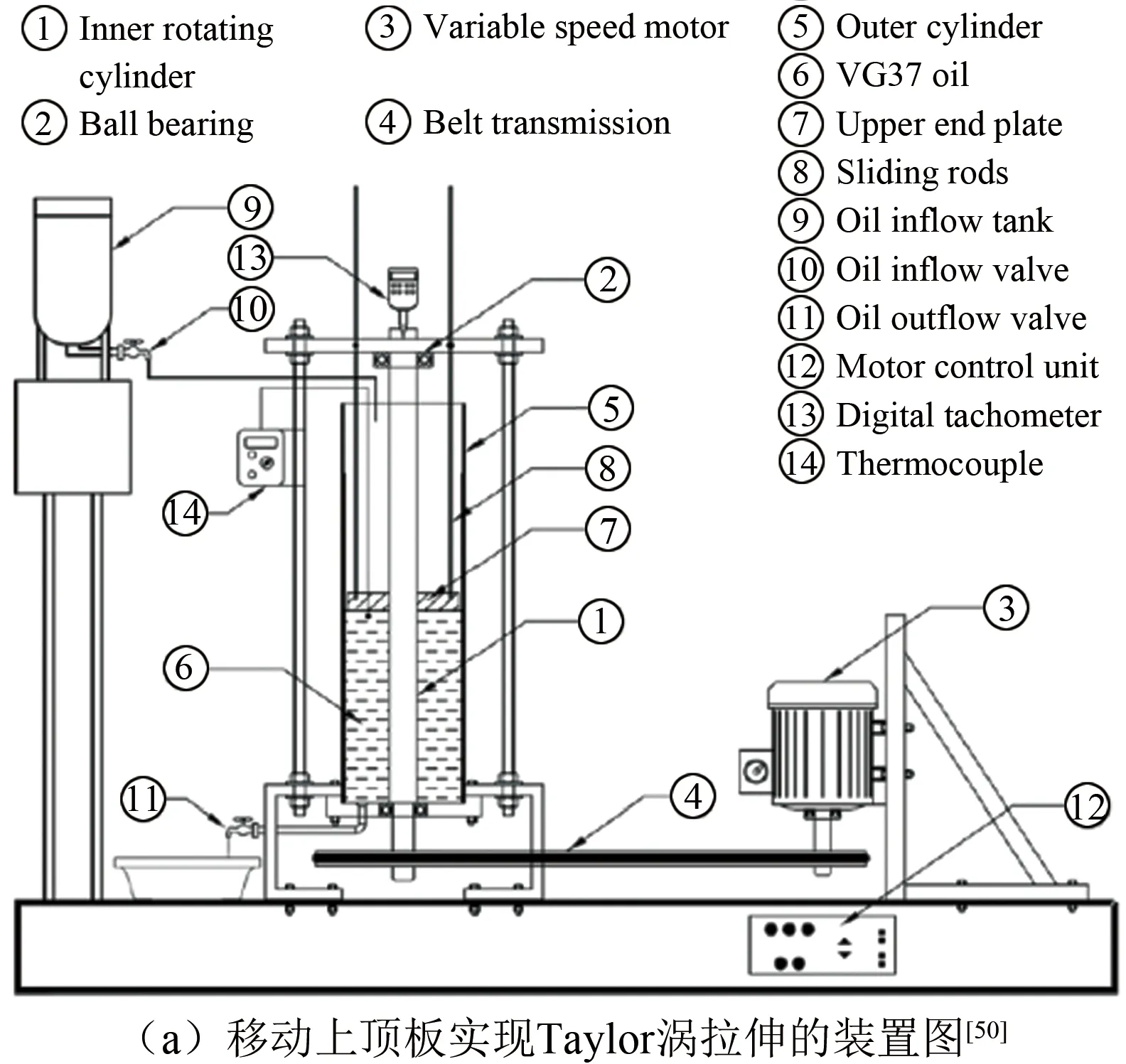
圖8 Taylor-Couette流動特有減阻方法Fig.8 Special drag reduction methods of Taylor-Couette flow

3 總結與展望

間隙之間充滿流體的同軸轉子在工程領域廣泛存在，屬于經典的Taylor-Couette流動結構。研究轉子減阻技術不僅有利于減少能源消耗，而且有助于擴展對Taylor-Couette流動結構的認識和減阻機理的了解。探索高效的旋轉圓柱減阻方法極富研究價值。目前仍有待加強的研究問題包括：

1) Taylor-Couette流動中氣泡[34-36]和高分子減阻方法[54]的機理探索。Taylor-Couette流動結構簡單、便于開展高精度實驗測試，可方便高效地進行轉子減阻的可視化研究。因此，利用Taylor-Couette流動可以進行氣泡減阻和高分子減阻的機理測試和探索，為管道流動和其他流動提供更多的參考。

2) Taylor-Couette流動復雜流場結構的進一步認識很大程度上可以促進旋轉圓柱間隙流動的減阻問題研究。比如，溫度梯度[55-57]、磁場梯度[58-59]等作用下的圓柱間隙流場結構仍不清楚；間隙內充入黏彈性流體[60-61]等非牛頓流體對流場結構的影響有待揭示。

3) 基于Taylor-Couette流動的復合減阻方法有待進一步探索，現有的Taylor-Couette流動減阻方法較為單一，可開展基于Taylor-Couette流動的氣泡超疏水耦合減阻方法等其他減阻方法研究。另外， Taylor-Couette流動特有減阻方法的系統研究相對較少，較低雷諾數條件下利用Taylor渦調控內轉子扭矩的方法有待進一步發展。