DA-LM 算法在MEMS 加速度傳感器誤差校正中的應用研究?

喬美英許城寬湯夏夏高翼飛史建柯

(河南理工大學電氣工程與自動化學院，河南 焦作454000)

MEMS 三軸加速度計因成本低、體積小、低功耗，廣泛應用于無人機、無人車、無人船、機器人、醫療輔助器械及隨鉆等設備[1]。 但由于受自身工藝及應用環境等因素，導致三軸加速度計測量精度嚴重降低，無法滿足高精度測量系統的要求。 隨鉆軌跡測量(Trace Measurement While Drilling，TMWD)系統利用MEMS 加速度計解算出的姿態角繪制軸跡，為保證所繪軸跡的準確性，需要不斷對提高加速度計解算精度的相關技術進行創新和優化，以減少實際作業過程中鉆孔真實軌跡與理想軌跡的偏差。

已有相關文獻給出加速度計的校正方法，例如加速度計的最大似然校正算法[2]，同時實現加速度計三軸非正交誤差的補償，補償的重點在于參數的精確估計，但該方法無法補償未對準誤差。 較為流行的基于橢球假設的三軸加速度計誤差標定與補償[3]，該方法也考慮了非正交誤差，使得測量精度更高，但橢球擬合法對于原始的數據要求較高，且無法彌補未對準誤差。 文獻[4]是矢量傳感器對非對準誤差及其校正，該方法利用橢球擬合及點積不變相結合的方法，彌補了橢球擬合不能校正非對準誤差的缺陷，但這種方法實現起來需要很高的實驗條件，且點積不變法對參考矢量精度有要求，否則算法效果不佳，并且該算法需要額外的矢量輔助運算，不利于校正單一傳感器。 高斯牛頓迭代算法[5]，其優點是操作簡單，優化速度快，但優化參數過多會發生部分參數局部最優情況，無法滿足所有參數一同得出最優解。 以上算法盡管在一定的條件下可以達到預期的效果，但存在以下問題:需要大量的實測數據；較多的數據易造成算法對數據的依賴性；面對非線性較強函數尤其是迭代參數較多的情況下，不加以約束易造成死循環，最終使得所有參數無法到達最優點。

針對上述問題本文利用Dragonfly Algorithm(DA)與Levenberg-Marquardt(LM)的聯合優化算法，DA是一種多群體智能優化算法，能夠實現目標參數的全局尋優，缺陷是局部搜索能力不高，但可以利用LM 算法強力的局部尋優能力再次優化參數。 校正之后的加速度計坐標系實現三軸正交，但在制造的過程中受到工藝水平的限制，加速度計與載體坐標系三軸之間存在未對準角度，表現為兩個坐標系之間存在旋轉矩陣，本文針對未對準問題給出補償策略，相較于傳統的方法易于實現。 為了提高數據的擬合效果，實驗采集數據時用等夾角法[5]旋轉雙軸轉臺，使數據在空間中呈均勻分布。

1 誤差分析和建模

MWD 的傳感器模型與通用的航姿參考系統(Attitude and Heading Reference System，AHRS)基本相同，因此MWD 的加速度計誤差模型也可以用統一誤差模型來表示。 MEMS 加速度傳感器在隨鉆中的布局可參見文獻[6]。 MEMS 加速度計誤差來源主要有比例系數誤差、零點漂移誤差、未對準誤差以及非正交誤差[7]等。 依據誤差來源寫為誤差模型:

U為加速度計不受誤差干擾的無偏值；D為比例因子誤差；T為未對準誤差；S為非正交誤差；B為加速度計偏差；V為加速度計測量值。 在使用DA-LM 估計誤差參數時，暫不考慮未對準誤差T。讓SD＝K，由式(1)可得:

通過求得K及B矩陣參數可實現對加速度計誤差補償。

1.1 誤差模型變換

加速度計輸出三個數據量:Vx，Vy，Vz分別對應當地重力場x，y，z三個方向的分量。 對式(1)展開可將加速度計的誤差矩陣方程寫為:

ux，uy，uz為真實重力場分量；εx，εy，εz為非正交誤差參數；fx，fy，fz為加速度計三軸對應的比例因子誤差，Bx，By，Bz為三軸偏差值，其中以x軸的輸出Vx為例:

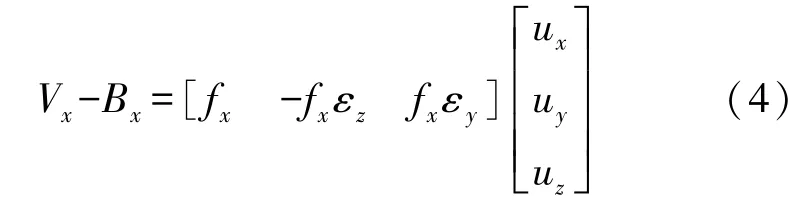
當地的重力場在加速度計的三軸投影:

｜g｜為重力加速度絕對值；α，β，γ分別對應重力三個方位之間的夾角[8]，式(5)代入式(4)寫為

利用式(5)、式(6)得出:

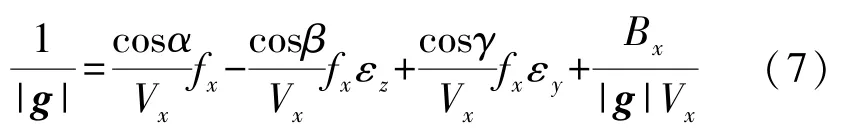
同理Vy，Vz也能夠寫成如式(7)的形式。 聯立可寫為等式:

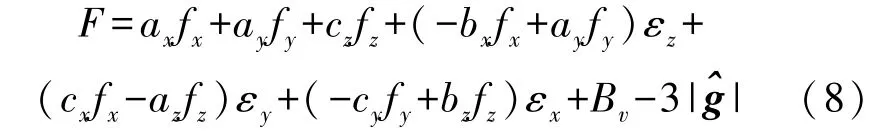
式(9)ax～cz為式(8)的輸入值，該輸入由加速度計的輸出提供。 LM 算法優化式(8)的誤差參數，該算法局部收斂能力很強但全局收斂能力較弱，因此DA 先作初始優化使誤差參數達到全局收斂，輸出的參數結果再用LM 優化。

1.2 初始參數選取

DA 是一種仿生學算法，它模擬蜻蜓在自然界中的靜態和動態蜂群行為[9]。 該算法利用蜻蜓的習性分為:分離、排隊、結盟、尋找獵物和躲避天敵這5 類行為。 算法中的參數值:分離權重、對齊權重、凝聚權重、獵物權重因子、天敵權重因子作為蜻蜓的行為度，以更新蜻蜓的位置，該算法的優勢是能夠改善給定問題的初始隨機參數，收斂于全局最優值。

初值優化算法采用橢球方程給出評價函數[10]，因為經仿真分析DA 與橢球擬合的聯合校正法可以消除零偏誤差及白噪聲的干擾，并且方程簡便，易于處理。 式(2)作平方可得:

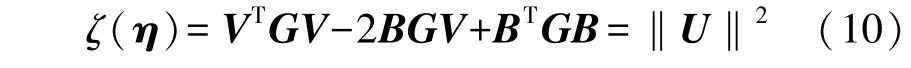
G＝(K-1)T·K-1＝sTs，構造DA 的評價函數:

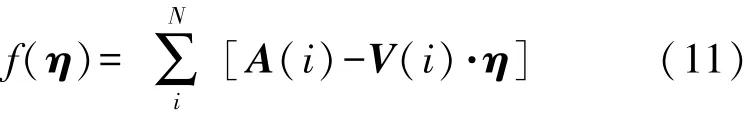
式中:A＝‖U‖2是加速度計無偏模值的平方，V＝(V2xV2yV2zVxVyVyVzVzVxVxVyVz)，η＝(abcdeflmng)T，a～g是帶有誤差信息的橢球參數。 DA 求解(11)中的參數向量η，可構成如下矩陣:

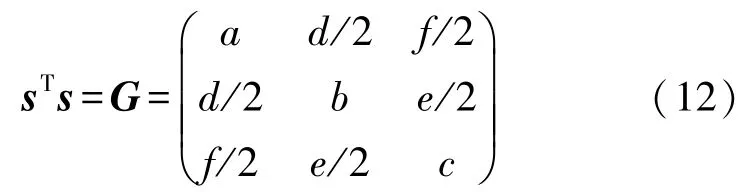
s可通過奇異值分解求得:

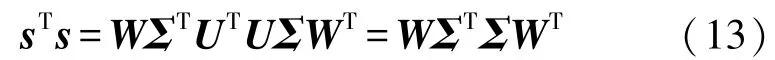
ΣTΣ為G的特征值組成的對角陣，W是G特征值對應特征向量組成的矩陣，因此s寫成:

求得偏差B:

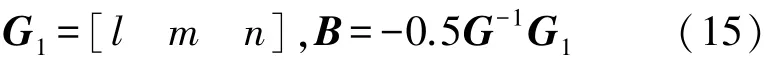
根據式(2)可獲得經過DA 優化的無偏值U′:

根據式(3)求得LM 算法的初值:

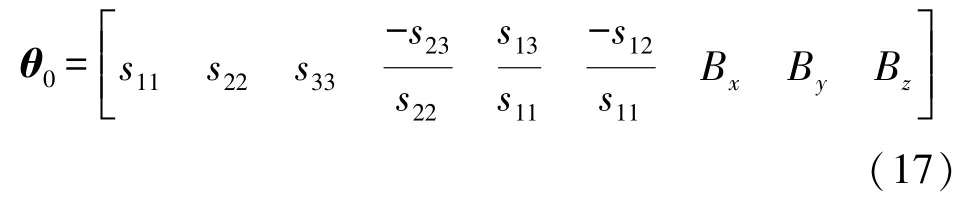
在DA 優化后的參數結果中，經過仿真實驗，偏差B可精確求得，所以待優化的誤差參數由原先的9 個變為了6 個:

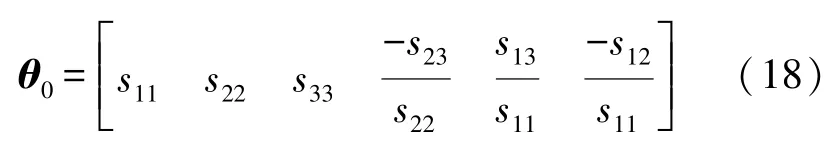
其值分別對應于誤差參數fx～εz。

2 LM 最優估計

LM 法是解決非線性最小二乘問題的一種方法，獲得非線性方程的最優解。 LM 算法同時具備梯度及牛頓法的特征，對于連續微分的線性系統，LM 法可以通過更改步長找到局部最優解。 首先定義幾個參數:Jk是對應于θk的Jacobi 矩陣，dk是每次更新θk的步長，優化精度εk＝1e-4，λk是學習因子，αk是增益系數。

2.1 LM 算法實現流程

Step 1 經過1.2 重新定義目標函數:

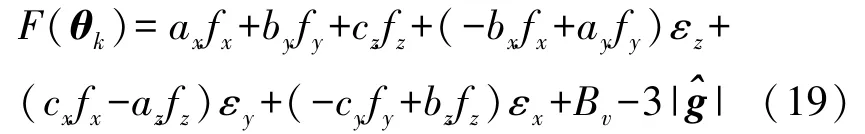
Bv已成為無偏量，θk作為初值，計算Jk，并且令λk＝1/N×trace(JTk·Jk)為初始學習因子:Step 2 如果‖JkF(θk)‖≤εk，停止迭代，輸出估計的參數值。 如果條件未達成，則計算步長:

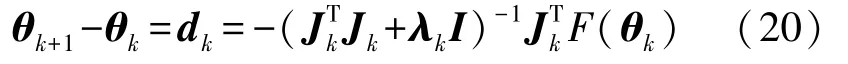
I是與Jk具有相同階數的單位矩陣。F(θk)對每個待求參數求偏導:

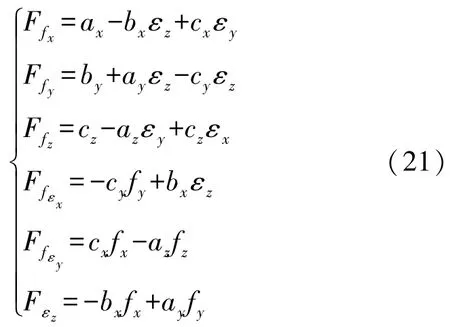
n個數據6 個參數構成n×6 的雅可比矩陣Jk。

Step 3 計算增益系數:

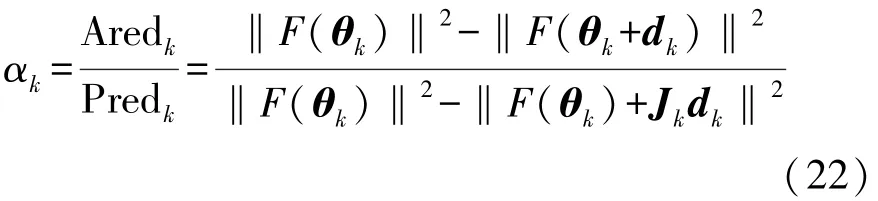
如果αk>0，則θk＋1＝θk＋dk；若不滿足該條件，則θk＋1＝θk。 Aredk表示目標函數實際差值，Predk表示目標函數預測差值。αk用來檢驗當前預測參數的好壞。 更新λk:

Step 4 令k＝k＋1，并返回Step 2。

2.2 LM 算法改進

實際獲得的數據帶有噪聲等不確定因素的影響，在第1 節給出誤差模型，沒有考慮時變等誤差[11]，這些誤差將直接作用于原始數據，數據的異常使得雅可比矩陣Jk出現偏差，隨著時間的推移，更多的異常值最后會導致算法局部尋優失效。 因此LM 算法的核心是調整學習率，其目的是實現兩種算法適當的組合:梯度下降法的一致誤差減小與高斯-牛頓算法的局部收斂性。 所以重點是對學習率λk的調整。 本文使用一種新穎的λk調整策略[12]:

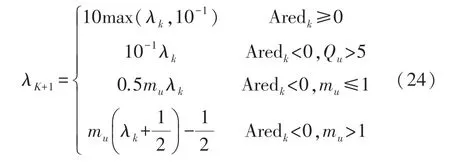
式中:mu＝max[0.4，min(αk，10)]，Qu為:

式(22)至式(24)對于學習因子λk的策略相比于式(22)增強了收斂性，對于二次方的目標函數提高了收斂速度。 求得的誤差參數通過式(2)進行補償。 綜上所述DA-LM 算法流程如圖1 所示。

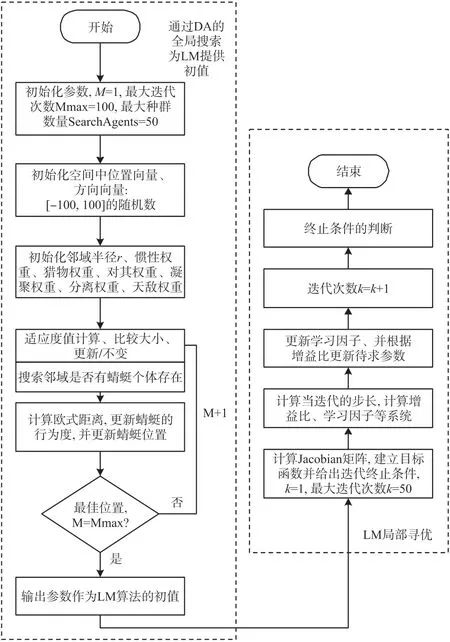
圖1 DA-LM 算法流程圖

3 未對準誤差校正

3.1 未對準誤差分析

未對準誤差是傳感器坐標系與載體坐標系之間的三軸未對準偏差[13]，第1、2 小節DA-LM 估計并未考慮未對準誤差，而傳感器框架的未對準會大大降低導航系統的準確性，在常規的校準策略中無法確定這些失準，但是可以將該誤差與加速度計其他誤差區別開來進行估計。 該誤差來源主要由安裝工藝造成，如圖2 所示，其中G代表加速度計坐標，P代表載體坐標。

圖2 加速度計及載體之間的未對準

對于未對準校準策略，如地磁場矢量與重力場矢量之間的恒定角度求得旋轉矩陣[14]，但是該方法需要額外的磁傳感器信息作為輔助，利用已知的無偏地磁場信息校準傳感器，分別旋轉平臺的三個坐標軸導出旋轉矩陣。 這種方法對于校準設備要求較高，每次校準都需要平臺的一個軸與地磁場相應方向對準。 但是對此方法可作改進運用于加速度計的校準。

3.2 未對準校正策略

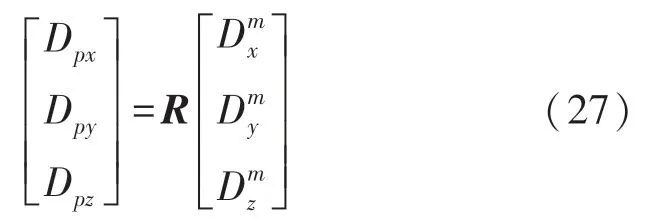
定義加速度傳感器框架為一個正交框架:Dm，定義平臺框架為Dp。Dm與Dp三軸之間存在有小角度(δxy，δyz，δxz)，所以平臺框架相對于正交框架存在一個旋轉矩陣R:是加速度計測量值，Dpx，Dpy，Dpz是地球重力場的三個分量。 定義[px，py，pz]分別為平臺的三個旋轉軸。 首先繞py軸旋轉，此時Dpy輸出為常值，收集加速度計數據，然后通過最小二乘法估計:

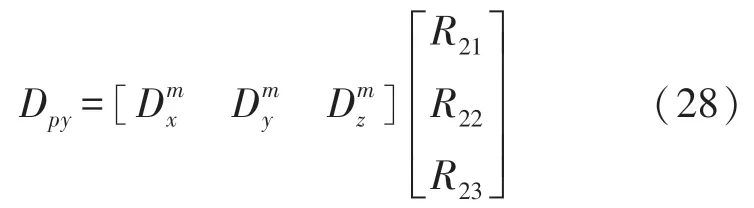
R21，R22，R23分別為R第二行參數，通過該行參數可以求解第一行參數，加速度計數據可求得橫滾角γ，而因此有:

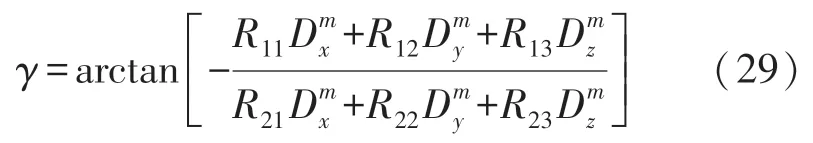
γ作為真實的橫滾角，使平臺處于不同的姿態，收集傳感器數據，利用最小二乘法估計R的第一行參數。 同理，利用俯仰角及前兩步估計的參數可求得R第三行參數:

式中:θ為真實的俯仰角數值，該值通過θ＝求得，旋轉矩陣R的所有參數均已求出。 該校準策略的優點是不需要平臺的每個軸都與參考矢量的方向對齊。

4 實驗及結果分析

4.1 仿真實驗

MATLAB 仿真實驗，單位球面上均勻取點，每個點對應在球面上的各個方向，采用等夾角均勻取點法形成64 個點，設置的誤差參數如表1 所示。

表1 誤差參數設置

將以上參數作用到數據點上，生成加速度干擾數據。 用DA 獲得誤差參數初值，首先需要設置DA初始參數，如表2 所示。

表2 DA 初始參數設置

當數據未加入旋轉矩陣干擾的優化結果如表3所示，可以看出優化的部分參數能夠達到設定值，不過有些參數與設定值偏離較大。 但是DA 能為下面的工作提供強有力的幫助:能夠精確估計偏差，獲得橢球參數的全局最優解，這為LM 算法提供了良好的初值運算。

表3 加速度計校正參數(未加入旋轉矩陣)

當數據加入了旋轉矩陣干擾的優化結果如表4。

表4 加速度計校正參數(加入旋轉矩陣)

為了凸顯算法的作用，根據不同情況分別給出仿真結果，如圖3～圖7。

圖3 原始與干擾數據

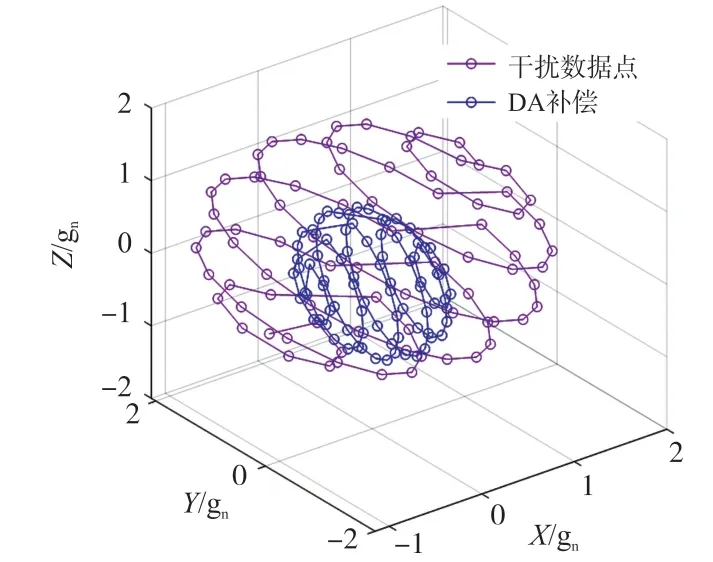
圖4 DA 補償數據

圖5 LM-DA 補償數據

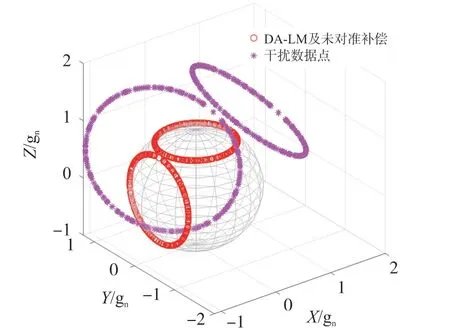
圖6 未對準補償

圖7 算法綜合對比

圖3加入了誤差參數的數據呈現出傾斜的橢球體，所有數據點都偏離了單位球體，因偏差的作用干擾數據的原點偏離了中心坐標點，比例因子，非正交誤差與未對準誤差讓球體發生了畸變，數據點的模值均大于1。

圖4 中，經過了DA 優化的數據球體大小驟減明顯，全局搜索已起到作用，并且校正后的球體圓點已在坐標軸中心，但是球體依然處于傾斜狀態，由于不能完全校準參數，使得大量數據其模值小于1。

圖5 所示LM 優化DA 的結果參數，球體幾乎恢復正常情況，數據點的模值均在1 附近，但是LM 優化后的球體依然處于傾斜狀態，因為目前還未校正未對準誤差。

圖6 中是對數據點分布在不同方向的擬合情況，在這一步中已加入了3.2 小節的未對準校正策略，可以發現經過了旋轉矩陣R的補償后，干擾后的數據點能夠擬合在球面上。

圖7 所示經過DA 的數據集能夠回到坐標軸中心，但數據分布在單位球體的內部，再次運用LM 算法可以將數據集擬合在球面上，但是與原數據的分布在方向上有偏差，經過旋轉矩陣R的補償，受干擾的數據集能夠擬合到原數據集上。 在有關磁傳感器的校正方法中[15-18]同樣能夠獲得類似于圖3～圖7 的仿真結果，但本文校正策略不適用于磁傳感器誤差校正，因為額外存在的軟硬誤差，無法建立起1.1 小節的誤差模型，必須給出針對性的校正方法實現類似于本文圖5 的仿真結果。 但本文給出的對準策略能夠用于磁傳感器，實現類似于圖7 的仿真結果，這為以后校正磁傳感器的工作提供幫助。

4.2 實測數據驗證

為進一步驗證算法的有效性，采用自主研發的隨鉆測斜儀進行現場實驗， 該測斜儀主要由STC15F60S2 單片機；ADI 公司推出的基于iMEMS 技術的三軸、數字輸出加速度傳感器:ADXL345；還包括震動傳感器、Flash 存儲器(w25x16)、外部時鐘模塊(DS1302)、藍牙模塊(hc-06)、鋰電池(18650)及本安型的電源電路等組成。 其中ADXL345 加速度計傳感器擁有最高13 位分辨率，功耗小，靈敏度高，最高達3.9 mg/LSB，以及量程可變范圍廣等優點。 實驗過程中ADXL345 測量的數據通過UART 協議傳輸到單片機，并存儲到Flash 中，最后由藍牙發送到上位機，用MATLAB 語言編寫代碼處理數據。 隨鉆測斜儀外殼，及內部的測量短節如圖8 所示。

圖8 隨鉆測斜儀

4.3 參數擬合校正

測斜儀安置固定于無磁轉臺上，如圖9 所示。操作上位機使轉臺處于不同姿態，通過加速度計獲得轉臺在不同姿態下三個方位的重力分量。

圖9 雙軸轉臺

轉臺X，Y，Z三軸分別轉過一定角度，操作轉臺使其俯仰角、航向角旋轉次數、航向角間隔分別為:30°，8，45°；60°，14，25.7143°；90°，16，22.5°；120°，14，25.7143°；150°，8，45°；180°，1。 存儲芯片共記錄以上68 個加速度計輸出點。 利用本文提出算法估計誤差參數，其結果如表5。

表5 加速度計校正參數結果

4.4 俯仰角補償結果

分別采用不同算法補償誤差參數:①單獨采用DA補償數據點，不采用LM 法與未對準補償；②DA-LM擬合數據，不采用未對準補償，；③采用DA-LM 并加入未對準補償。 三種補償方式的實驗結果依次見圖10～圖12。 在圖10 可以發現DA 擬合的數據點可以補償誤差，俯仰角誤差有所減小，但是部分誤差角仍然較大，因為DA 可以估計傳感器誤差參數，但是由于局部尋優能力較差，部分誤差參數并不能估算出最優解，尤其是不能校正未對準偏差。 圖11 經過了DA-LM 的優化其俯仰角誤差明顯減小，DA 提供的初值給予LM 很大的幫助，LM 優秀的局部搜索能力能夠快速找到極值點，誤差參數的估計精度有所提高。但是加速度計與測斜儀之間的三軸未對準角度影響加速度計角度的解算。

圖10 DA 補償結果

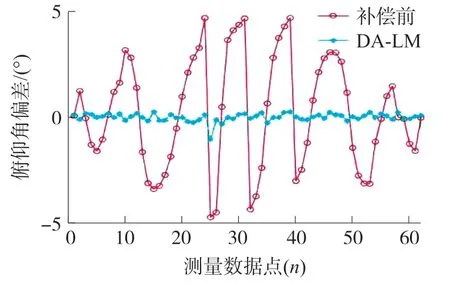
圖11 DA-LM 補償結果

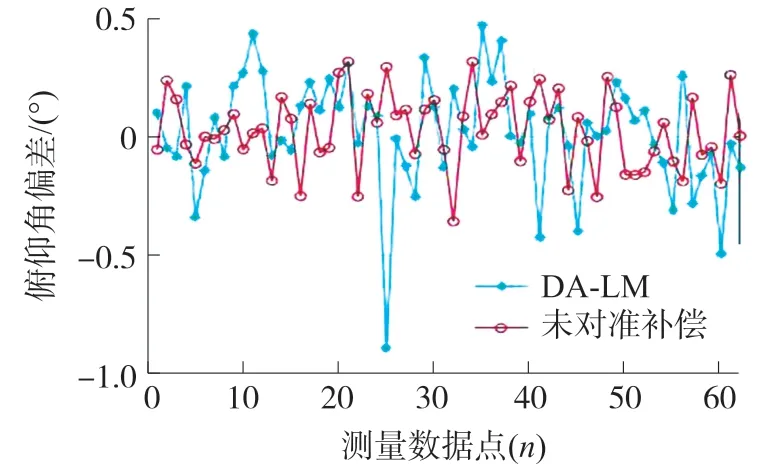
圖12 DA-LM 及加入未對準補償的結果

加速度計與測斜儀三軸存在角度偏差，因此加速計坐標系與測斜儀坐標系之間存在一個旋轉矩陣。 圖12 所示沒有經過未對準補償的部分數據點仍然存在較大偏差，在20～30 測量數據點之間俯仰角誤差達到0.85°。 用3.2 小節的未對準策略，旋轉轉臺的X軸，讓Y軸上升20°，然后旋轉Y 軸估計旋轉矩陣的第二行元素，然后隨意旋轉平臺的三軸分別估計旋轉矩陣的第一行和第三行元素。 圖12 中補償結果明顯，俯仰角不存在較大的偏差值。 補償前俯仰角最大誤差為4.7°，補償后俯仰角最大誤差為0.39°，其精度提高了一個數量級。

4.5 橫滾角補償結果

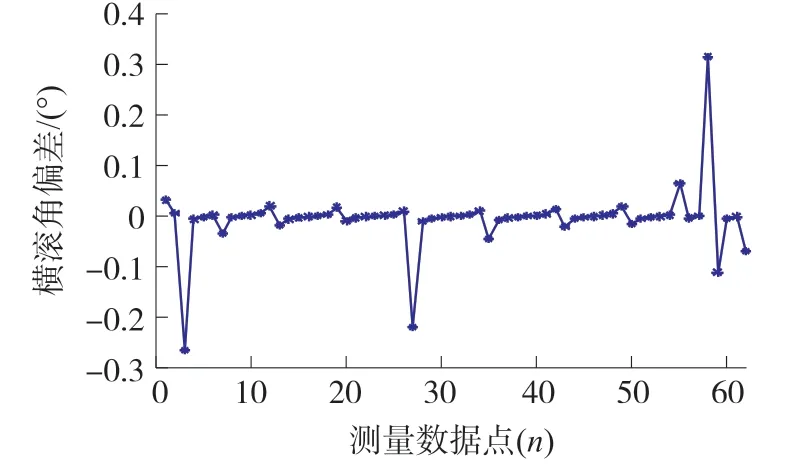
圖13 轉臺水平旋轉橫滾角誤差

轉臺保持水平不變，讓轉臺Z軸旋轉一周取得62 個數據點，觀察加速度計解算橫滾角的情況。 如圖13 所示，橫滾角在其起始旋轉階段及結束旋轉階段偏差較大，最大偏差超過了0.3°。 在置于平臺俯仰角分別為30°(水平旋轉8 次)；60°(水平旋轉14次)；90°(水平旋轉16 次)；120°(水平旋轉14 次)；150°(水平旋轉8 次)；180°(水平旋轉1 次)時分別記錄橫滾角輸出(如圖14 所示)，橫滾角最大偏差達超過了0.9°，能夠說明俯仰角對橫滾角的解算是有影響的，尤其是未對準誤差，經過DA-LM 并加入未對準補償的情況如圖14。

圖14 補償前后橫滾角誤差

可以看出補償結果明顯，說明傳感器誤差能夠有效估計，可將橫滾角誤差控制在0.3°左右。 以均方根誤差(Root Mean Square Error，RMSE)衡量校正前后加速度計解算姿態角的偏差。

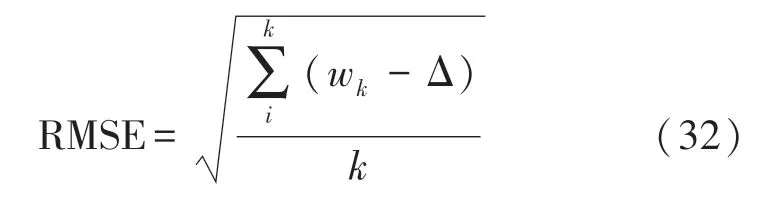
式中:wk代表實驗中真實的俯仰角與橫滾角，Δ代表由三軸加速度計解算得到的俯仰角及橫滾角。

由表6 所示，本文整套算法優于DA-LM 算法，證明未對準對姿態的解算影響不小。 本文提出的整套算法相比于DA 估計精度提高了4 倍。

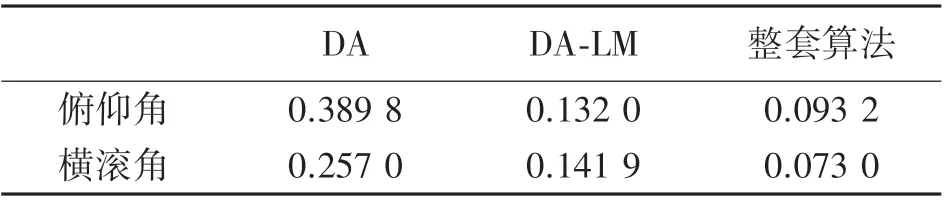
表6 不同補償下姿態角的均方根誤差

圖15 所示，校正后的數據點模值正常，同時也證明了本文算法的有效性。

圖15 校準前后重力場模值比較

4.6 算法計算效率

由圖1，DA 中適應度值計算至更新蜻蜓位置的迭代環節決定了該算法計算效率，最大迭代次數Max 越大算法運行時間越長；LM 算法運行效率的高低在于增益系數αk的計算、參數θk以及學習率λK更新，但LM 算法本身計算效率較高，且本文所用λK的更新策略極大提高了算法的收斂速度，故LM在計算效率方面要遠高于DA。 采用雙軸轉臺實驗數據驗證DA-LM 算法的計算效率，DA 最大迭代次數100，LM 算法最大迭代次數500，用MATLAB 中etime( )與clock 的組合代碼計算程序運行時間。驗證計算效率時不考慮未對準策略，因為該策略采用的是最小二乘估計，輸出結果很快，對本文整套算法的運行時間無太大影響。

表7 所示，LM 算法相比于DA 其運行效率超出60%，但DA-LM 算法整體運行時間不超過3 s。

表7 不同算法運行時間

5 結論

本文通過對加速度計的誤差建模，分析誤差參數與誤差方程的關系，提出DA-LM 算法。 首先利用DA對誤差參數的全局尋優然后利用LM 算法局部尋優獲得最優值，通過估計旋轉矩陣實現加速度計坐標系與載體坐標系的對準。 本文所提出對加速度計誤差的一種完整補償方案，從實驗結果可以看出，加速度計對俯仰角與橫滾角的解算精度明顯提高，證明該方法在隨鉆測量系統中的應用具有一定的參考性。