一種基于隨機解調結構的心電信號壓縮采樣方法?

劉繼忠嚴 旭

(南昌大學南昌市醫工結合技術研究重點實驗室，江西 南昌330031)

可穿戴式心電監護系統的采樣過程主要依據香農采樣定理[1]，該定理會導致采集的數字信號包含有效信息和冗余信息，可經過壓縮去除無效信息，以方便后續存儲、傳輸等過程。 若能將采樣和壓縮融于一體，不僅可以避免后續數據壓縮處理，而且可以降低信號采樣頻率。 近年來Donoho[2]、Candès[3]和Tao 共同提出壓縮感知理論(Compressing Sensing，CS)，該理論將采樣和壓縮融合，是面向信號稀疏域采樣的非均勻采樣理論。 然而，CS 理論還主要停留在處理數字信號上，需以奈奎斯特頻率采樣模擬信號再以CS 理論壓縮，并未體現降頻采樣的應用優勢。 因此，模擬信息轉換器[4](Analog-to-Information Convertor，AIC)以CS 理論為基礎，以物理結構實現CS 的壓縮采樣過程，達到亞奈奎斯特頻率采樣信號的目的。 目前，AIC 主要可通過隨機采樣器[5](Random Sampling，RS)、隨機濾波器[6](Random Filter，RF)、隨機解調器[7](Random Demodulator，RD)以及調制帶寬轉換器[8](Modulated Wideband Converter，MWC)四種方法實現。 其中，隨機采樣器缺乏充足的理論支撐，隨機濾波器中硬件結構復雜，而調制帶寬轉換器由多條隨機解調器采樣支路組成。

同時，由于人體心電信號頻率范圍為0.05 Hz～100.00 Hz，監護分析時采樣頻率多用400 Hz ～500 Hz，若能降低人體心電監護設備的采樣頻率，可降低設備的采樣功耗、數據存儲功耗和數據傳輸功耗，有利于監護設備的續航能力[9-10]。 因此，文中針對健康監護中的心電信號，基于團隊前期基礎[11-12]，并考慮到可穿戴設備的低功耗性和便攜性，提出了一種基于隨機解調器結構的心電信號壓縮采樣方法，達到低數據量和高重構精度的要求。

1 基于隨機解調器結構的壓縮采樣構建

1.1 CS 采樣理論

1.1.1 信號稀疏表示

CS 理論可直接對數字信號的壓縮采樣，但要求信號本身稀疏或在變換域稀疏，對于數字信號x∈RN×1投影到正交基Ψ∈RN×N得到變換系數向量s∈RN×1，如式(1)，若對于00，系數s滿足式(2)，可認為x在變換域是稀疏的。

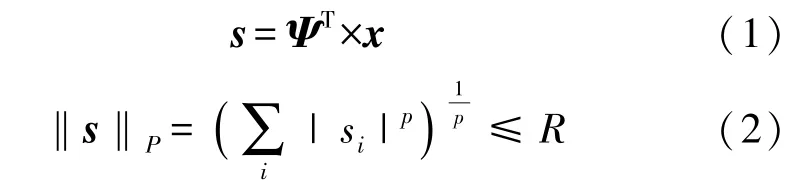
式中:x為心電信號，定義Ψ為稀疏矩陣，s為心電信號稀疏表示。 且定義投影稀疏度K如下:對于向量s∈RN×1，s中僅有K個元素大于閾值γ，γ→0＋，則K為信號x投影到矩陣Ψ上的稀疏度，其余N-K個元素小于閾值γ接近于零。

1.1.2 觀測矩陣采樣

CS 理論中，N維數字信號經過觀測矩陣Φ(Φ∈RM×N，M?N)可以降維到M維，得到測量值y，如式(3)、M值的確定如式(4)。 由式(1)、式(3)可得式(5)，實現信號x的壓縮采樣。

式中:y為測量值向量，y∈RM×1。

式中:K為稀疏度。

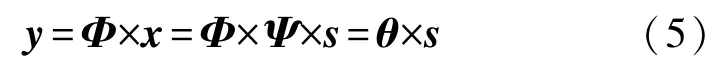
式中:θ為感知矩陣，將信號稀疏投影并在稀疏域上完成壓縮采樣，θ＝Φ×Ψ，θ∈RM×N。

在M?N的情況下，觀測矩陣Φ同時完成信號的采樣和壓縮，將信號從N維壓縮到M維，去除冗余信息且保留原N維信號的有效內容，以確保在重構階段可以完整恢復出N維信號。 后經Candès、Tao 等人[13]證明矩陣Φ須滿足約束等距特性(Restricted Isometry Property，RIP)才能在重構階段高概率近乎完整恢復出原始信號。RIP準則如式(6):

式中:ζS為 有 限 等 距 常 數(Restricted Isometry Constant，RIC)，要求0≤ζS≤1。 由于RIP 準則中ζS較難計算驗證，后Donnoho 證明觀測矩陣Φ滿足RIP 特性等價于觀測矩陣Φ與稀疏基Ψ不相關，兩矩陣相關性數學定義如式(7):，當u(Φ，Ψ)→1 時，觀測矩陣Φ和稀疏基Ψ相關性越小，矩陣Φ以更高的概率滿足RIP 準則。

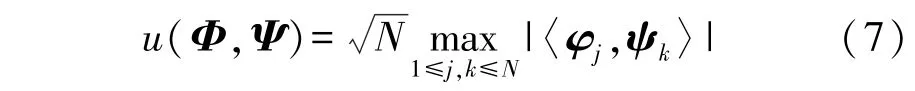
1.1.3 信號重構

在重構階段，以觀測矩陣Φ、稀疏矩陣Ψ和測量值y作為先驗條件，通過重構算法從M維測量值y恢復N維稀疏近似＾S，進而得到重構信號＾x。 重構過程是式(5)的逆向求解過程，由于M?N，可知求解方程為欠定方程，有無窮多解。 但稀疏表示s為K-稀疏的，方程(5)的逆向求解過程可轉換為?0最小化問題，如式(8)，與上節中信號稀疏投影相對應，稀疏度K越小，求解?0范數問題的逆向重構稀疏近似＾s越準確。

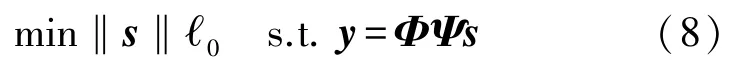
由于?0問題求解向量中非零元素的個數，屬于NP-Hard 問題，Donoho 將求解過程放大到?1最小化問題，將重構過程轉化為凸優化過程，如式(9)，主要以正交匹配追蹤算法(Orthogonal Matching Pursuit，OMP)為代表。

1.2 隨機解調采樣結構

1.2.1 隨機解調采樣理論

隨機解調采樣結構為CS 理論的物理實現，通過硬件實現觀測矩陣Φ的壓縮采樣功能。 在該結構中，信號x(t)需與偽隨機序列p(t)相乘混頻，要求p(t)中±1 元素分布隨機，且跳變頻率不低于x(t)的奈奎斯特頻率。 混頻信號經過低通濾波器后，ADC以亞奈奎斯特頻率采樣得到測量值向量y(m)，在重構階段以y(m)、對應硬件功能的觀測矩陣、稀疏矩陣和重構算法恢復信號。 結構整體如圖1。

圖1 隨機解調采樣結構

假設信號x(t)與偽隨機序列信號p(t)混頻后信號為y1(t)，如式(10)。 低通濾波器的單位脈沖響應為h(t)，混頻信號低通濾波相當于y1(t)與單位脈沖響應h(t)卷積，設濾波后信號為y2(t)，濾波(卷積)過程如式(11):

濾波后，對y2(t)均勻采樣，采樣間隔為TS，得到測量值向量y(m)如式(12)、式(13)，且m∈[1，M]。

假設信號x(t)以奈奎斯特頻率采樣得到x(n)，長度為N，x(t)在稀疏基Ψ下可線性分解如式(14):

結合式(13)、式(14)有式(15):

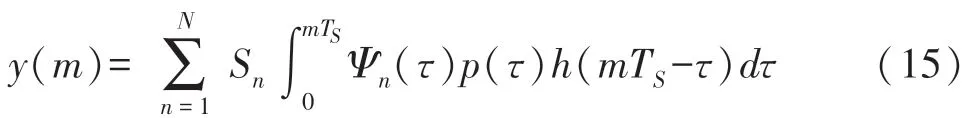
提取積分內容表達成式(16)，結合式(15)、(16)得式(17):

得到與式(5)一致的數學表示。 由式(14)、式(17)可知隨機解調結構基于CS 理論，其先驗條件與CS 一致，要求信號稀疏或在變換域下可稀疏，Sn為x(t)在Ψn(t)下的稀疏表示。θ＝[θm，n]M×N起感知矩陣作用，θ由稀疏基Ψn(t)、偽隨機序列p(t)和濾波器單位脈沖響應h(t)共同構成。

1.2.2 隨機解調器矩陣

CS 理論在重構階段需以觀測矩陣Φ、稀疏矩陣Ψ和測量值y為已知條件，依靠重構算法恢復＾x。在上述采樣結構中，信號與偽隨機序列在時域混頻、濾波截取低頻成分、低頻采樣得到y(m)，重構階段需依式(15)、式(16)和式(17)以p(t)、h(t)應構建觀測矩陣Φ，但式(16)中計算過程包含大量復雜積分計算，可將p(t)、h(t)離散化得到偽隨機矩陣P、單位脈沖響應矩陣H，構建觀測矩陣Φ＝H×P。

①假設偽隨機序列p(t)離散化后元素分布順序為P(1)、P(2)、…、P(N)，p(t)與信號x(t)以乘法器混頻，依相乘過程構建對角矩陣P如式(18):

②經雙線性變換法將模擬濾波器離散化得到相應數字濾波器的單位脈沖響應向量h(n)，離散化頻率需與偽隨機序列p(t)離散頻率一致，假設h(n)中元素順序為h(1)、h(2)、…、h(N)，依卷積過程可構建單位脈沖響應矩陣H如式(19):

定義c＝N/M為壓縮比，矩陣第k行元素為h(1)、h(2)、…、h(kc)倒序排列，余下元素依次補零，k∈[1，M]。 測量值向量y(m)長度為M，由于M?N，隨機解調結構實現對信號x(t)的壓縮采樣。

③x(t)在時域與偽隨機序列p(t)相乘，起到頻域卷積、混淆x(t)頻譜的效果，以濾波器截取混頻信號y1(t)的低頻成分，然后ADC 以亞奈奎斯特頻率均勻采樣。 采樣過程以信號頻域稀疏為前提，即稀疏矩陣Ψ為傅里葉逆變換矩陣。

1.2.3 隨機解調器結構采樣相位

為方便矩陣運算對比，采樣相位分析以x(n)為實驗信號。x(n)與偽隨機序列p(n)混頻得到信號y1(n)，假設模擬濾波器經雙線性變換法得到相應數字濾波器的單位脈沖響應為h(n)，y1(n)經濾波器相當于與h(n)卷積，假設濾波后信號為y2(n)，如式(20):

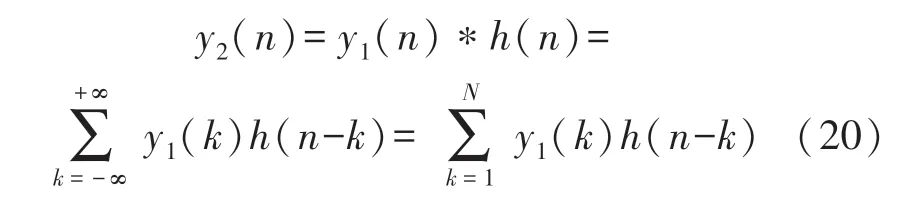
經間隔采樣得到y(m)(m＝1，2，…，M)，由上述內容可知，在隨機解調結構中需以濾波器求解單位脈沖響應構建脈沖響應矩陣H，y(m)與矩陣H關系如式(21):

可知y(m)中元素表達如式(22):

y(m)由y2(n)均勻采樣得到，若令式(20)、(22)相等，可知n＝mc＋1，既有式(23)、式(24)。

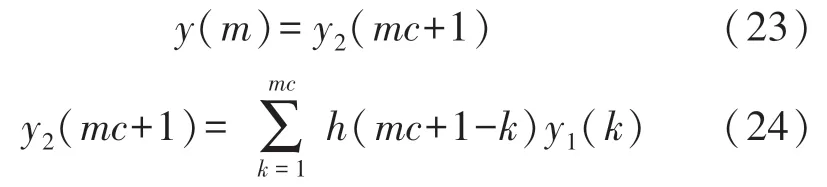
觀察y2 新表達式可知，由于mc≥1，式(24)中無y2(1)項，若令mc＝0，y2(1)中包含h(0)項，但h(0)不存在，即式(24)中y2(1)項不存在，需作調整如式(25)、式(26):

由上式可知，測量值向量y中第m項由y2(n)的mc項采樣得到，即y(1)＝y2(c)、y(2)＝y2(2c)等，同時，依據式(21)中矩陣運算，可知濾波后對y2(n)的均勻采樣過程中，采樣間隔為c、采樣相位為c-1。

2 心電信號隨機解調結構仿真實驗

2.1 偽隨機序列及濾波器模塊參數分析

本節實驗以MIT-BIH 數據庫中100 段心電信號前1 024 采樣點x(N＝1 024，信號持續時間為2.874 1 s)為實驗信號，以±1 隨機交替的p(n)為偽隨機序列。 數據庫中x為ADC 以奈奎斯特頻率采樣心電信號得到，相同時間內產生與x長度一致的偽隨機序列，可知二者的采樣頻率一致，符合隨機解調結構對偽隨機序列頻率的要求。

采樣得到測量值向量y(m)需借助算法得到重構信號＾x，文中采用均方根差百分比(percentage root-mean-squared difference，PRD)表征重構信號與實驗信號間的誤差，如式(27)，PRD 越小表明重構誤差越小。

同時，文中采用控制變量法，分析隨機解調采樣結構中各參數對心電信號重構誤差的影響，尋找適合心電信號的采樣結構。

其中濾波器模塊參與信號采樣環節，且重構階段以濾波器傳遞函數計算的單位脈沖響應矩陣H為觀測矩陣Φ的重要組成部分，即濾波器模塊對重構精度起決定性作用。 由于巴特沃斯濾波器(Butterworth Filter)通頻帶內頻率響應曲線相對更平滑，而在阻頻帶則逐漸下降為零，易于硬件實現，文中選用butterworth 低通濾波器，關鍵參數有濾波器階數和3 dB 截止頻率ωc。

以x為實驗信號，經混頻、濾波后使用downsample 函數以相應相位間隔采樣y2(n)。MIT-BIH 數據庫中心電信號采樣頻率為360 Hz，暫取c＝2、M＝512，間隔一位采樣相當于濾波后采樣率為180 Hz，由于低通濾波器截止頻率需低于采樣頻率的1/2，即濾波器截止頻率最高為90 Hz，重構以OMP 算法， 選用不同階數和截止頻率的Butterworth 濾波器采樣、重構，實驗結果如圖2。

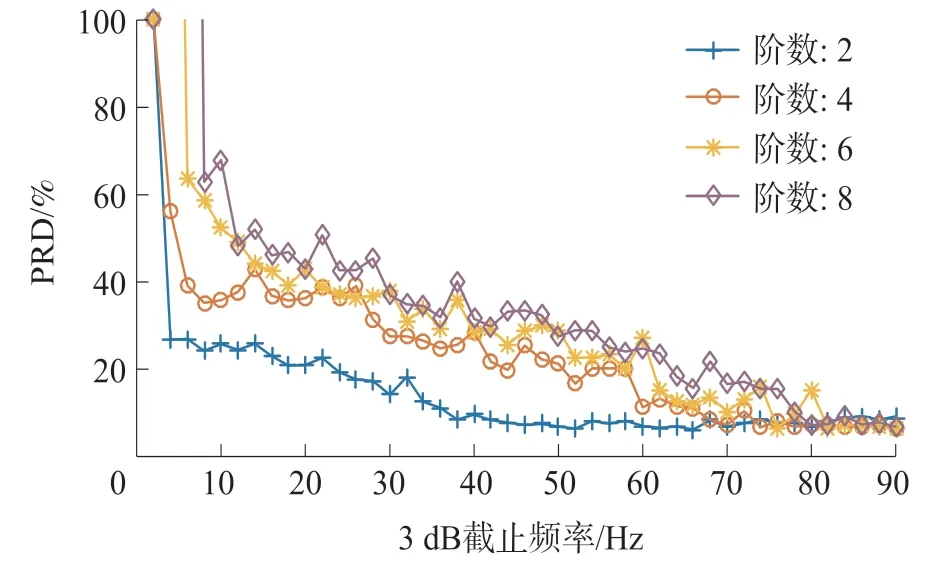
圖2 Butterworth 濾波器不同階數不同截止頻率心電信號重構誤差分析

由圖2 可知，在相同采樣頻率、重構算法下，不同階數和不同低通截止頻率ωc對應不同的重構精度，隨著ωc的增加，PRD 誤差曲線呈降低趨勢。

①當濾波器階數為2，在ωc≥50 Hz 時，重構PRD 誤差穩定在6%左右，ωc≤20 Hz 時，誤差較大，PRD≥20%。

②當濾波器階數為4，在ωc≥70 Hz 時，重構PRD 誤差穩定在6%左右，ωc≤50 Hz 時，誤差較大，不利于重構。

③當濾波器階數為6，在ωc≥80 Hz 時，重構PRD 誤差穩定在6%左右，ωc≤70 Hz 時，誤差較大。

現場共走訪牧民22戶，查看患病牲畜51頭。診治時正值冷季，病畜臨床表現主要為體格相對消瘦、食欲不振、被毛粗亂等，也存在眼臉、下頜及胸下水腫、食欲減退、虛弱以及容易疲倦等癥狀，少數病畜出現腹瀉、黃疸、腹膜炎等癥狀。病畜癥狀比較符合寄生蟲病的表現。

④當濾波器階數為8，在ωc≥80 Hz 時，重構PRD 誤差也穩定在6%左右，ωc≤80 Hz 時，誤差較大。

同時，各曲線間對比可知，隨著濾波器階數的減小，PRD 誤差曲線在更低的截止頻率處穩定，意味著后續采樣頻率可以更低。 而且濾波器階數的增加會加大相應硬件成本，從重構精度、后續采樣頻率和硬件成本角度，以2 階濾波器構建心電信號隨機解調采樣系統更合適。

2.2 信號長度及稀疏度分析

上述采樣實驗中，心電信號長度N＝1 024(時間為2.874 1 s)，MIT-BIH 數據庫中每段信號時間為10 s，共3 600 點數字信號。 本次實驗以N＝36 為起點(對應0.1 s 時域信號)，并以此為步長增加信號長度，考慮到穿戴設備心電信號單次采樣與重構的實時性要求，分析5 s 內信號長度對重構影響。

同時，重構算法需以測量值向量y，感知矩陣θ和稀疏度K為先驗條件，重構稀疏近似＾S，進而得到恢復信號＾x。 稀疏度K定義依據1.1 節，為投影向量s中僅有K個元素大于閾值γ，γ→0＋，則K為信號x投影到正交基Ψ上的稀疏度。 上述實驗中取γ＝0.05，為驗證γ取值對重構精度的影響，對相同長度信號取不同γ值，在濾波器階數為2、截止頻率為90 Hz、壓縮比c＝2 條件下重復重構過程，實驗結果如圖3。

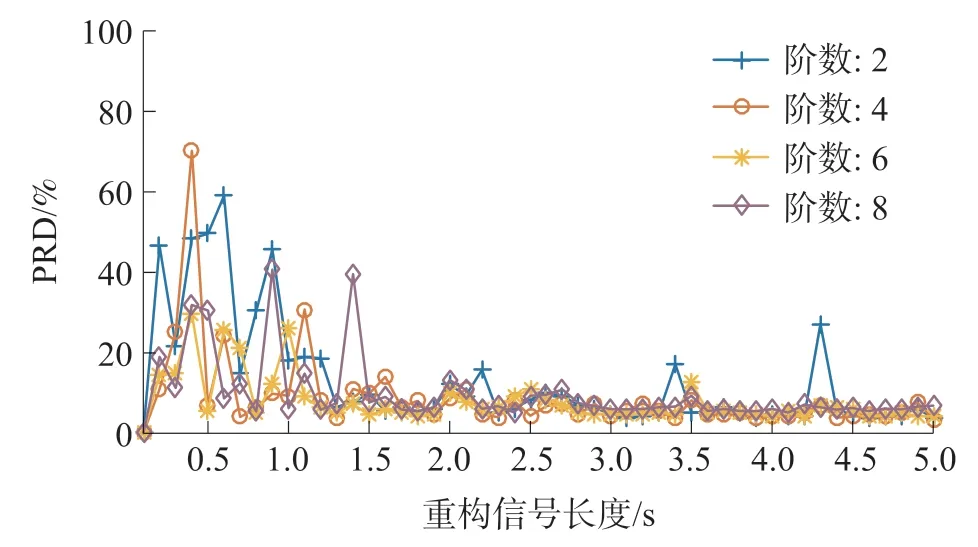
圖3 不同時間長度、稀疏度信號重構分析

依圖3，從時間角度分析，當采樣信號低于1.5 s(N≤540)時由隨機解調結構得到的采樣值重構心電信號精度不穩定，誤差變化幅度較大。 采樣時間在1.5 s～2 s 內時，重構誤差較低且變化幅度小。2.0 s～2.8 s 內誤差波動較大但2.3 s 時重構誤差較小。 采樣時間大于2.8 s(N≥972)時，重構誤差較低且數值穩定。

從閾值γ角度分析，γ并非取值越小重構精度越高。 圖中γ＝0.01 時，信號重構PRD 誤差曲線波動較大，且重構相同時間長度信號時誤差并非最低。同時，γ＝0.07 時重構誤差稍高于其他兩種情況，而γ＝0.03 時稍低于γ＝0.05 的誤差值。

綜上，單次采樣時間可選擇1.5 s～2.0 s 或2.8 s以上，γ＝0.03。 但時間的增長造成重構中相關矩陣維數增加，計算復雜且耗時增長，可依據硬件情況和實時性要求選擇合適的單次重構時間長度。

2.3 壓縮比分析

上述采樣中，c＝2，濾波后間隔一位采樣，相當于采樣頻率為180 Hz，由于c＝N/M，理論上c可取[1，＋∞]范圍內任意數值，但c取小數時，由式(19)構建的矩陣H元素分布異常，會造成重構誤差較大，即隨機解調結構中c一般取正整數構建脈沖響應矩陣H。

依據2.1、2.2 節分析，選取2 階濾波器、N＝1 024、γ＝0.03，分析不同c值對重構PRD 誤差的影響(不同c值，對應不同采樣間隔和不同采樣頻率，c越大，采樣頻率越低，而采樣頻率需高于濾波器截止頻率兩倍，因此本節實驗設置截止頻率ωc＝c對應采樣頻率/2。

同時，當1 024 不為壓縮比c的整數倍時，調整實驗信號長度N＝(1 024/c的商)×c，以降低N取值不同對結果的影響。 實驗結果如下:

①c＝2，濾波后間隔一位采樣，對應隨機解調結構采樣頻率為180 Hz，PRD＝4.047 5%。

②c＝3，濾波后間隔兩位采樣，對應采樣頻率為120 Hz，PRD＝7.981 5%。

③c＝4，濾波后間隔三位采樣，對應采樣頻率為90 Hz，重構時PRD＝47.495 9%。

上述對比可知，取c＝2 可得較高重構精度，對心電信號采樣頻率可降低為180 Hz。

2.4 重構算法分析

上述重構過程都基于OMP 重構算法恢復心電信號，Donoho 提出OMP 重構算法后，又有學者在此基礎上提出新的重構算法，分別有:廣義正交匹配追蹤[14](Generalized OMP，GOMP)、稀疏度自適應匹配追蹤算法[15](Sparsity Adaptive MP，SAMP)、分段正交匹配追蹤算法[16](Stagewise OMP，StOMP)、正則化正交匹配追蹤算法[17](Regularized OMP，ROMP)、壓縮采樣匹配追蹤算法[18](Compressive Sampling MP，CoSaMP)和子空間追蹤算法(Subspace Pursuit，SP)。

本節尋找適合心電信號隨機解調采樣結構的重構方法，以上述算法為基礎，同時使用求解?1范式問題的l1_magic 工具箱，在Win10 Intel Pentium 3556U 1.7 GHz 和MATLAB 2016 平臺上以2 階Butterworth 濾波器、截止頻率ωc＝90 Hz、壓縮比c＝2、實驗信號長度N＝1 024、閾值γ＝0.03 條件下，重復10 次采樣心電信號并用不同算法重構，記錄重構結果的PRD 均值、PRD 標準差及重構耗時，實驗結果如表1。

表1 不同算法重構心電信號實驗結果

分析表1 可知，在隨機解調結構相同采樣條件及相同壓縮比下，從PRD 誤差角度分析，OMP 算法重構精度較高，GOMP、SAMP 和StOMP 算法次之。從重構穩定性角度分析，GOMP、SAMP 和SP 算法在重復采樣重構過程中PRD 標準差相對較小，即重構結果差異較小。 從算法運行時間角度分析，ROMP、GOMP 和StOMP 算法運行時間較短，能實現快速重構，但ROMP 算法重構PRD 誤差較大，不適合作為信號恢復算法。 本文主要考慮高精度重構，重構選用OMP 算法。

2.5 信號源分析

上述實驗基于MIT-BIH 中100 號心電信號，為進一步驗證隨機解調結構可壓縮采樣人體心電信號，隨機選取MIT-BIH 數據庫第105 號、115 號、122號、205 號、220 號五組心電信號作為新實驗信號。采樣結構參數與2.4 節中一致，依2.2 節結論，選取N＝1 024，重構選用OMP 算法，實驗結果如表2。

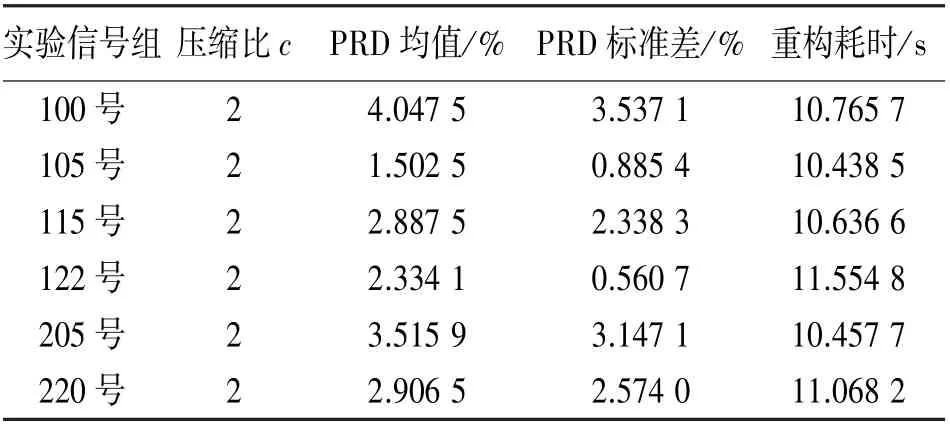
表2 不同心電信號重構實驗結果

依表2 可知，隨機解調采樣結構在c ＝2 時，對數據庫中不同組心電信號，重構精度在96.0～98.5%之間，具有較高的重構精度，PRD 標準差在0.6～3.5 之間，由于選用相同重構算法，重構耗時穩定在11 s。

3 總結與展望

針對可穿戴裝備心電信號實時監測中的大數據量、高功耗問題，本文提出并探討研究了基于隨機解調結構的心電信號壓縮采樣方法和實現過程，分析了采樣結構中采樣相位、濾波器參數、采樣頻率、重構算法等對心電信號壓縮采樣及后續重構精度的影響。 經理論推理和仿真實驗，為實現有效壓縮采樣心電信號，隨機解調結構中低通濾波器階數可為2，截止頻率可為90 Hz，壓縮比c 設置為2，采樣相位為c-1，對應采樣頻率為180 Hz。 同時，單次采樣重構時間可選擇1.5～2 s 或2.8 s 以上，重構以OMP算法，對不同人體心電信號的重構精度為96.0%～98.5%之間，具有較高重構精度。

文中以高精度重構為前提，實現隨機解調結構以180 Hz 采樣心電信號，低采樣率可降低監護設備的采樣功耗、數據存儲功耗和數據傳輸功耗，有利于提升設備的續航能力。 下一步將繼續改進采樣結構和重構算法，以提高重構精度、提升壓縮比，進一步降低心電信號的采樣頻率。 同時，降低算法的時間復雜度，縮短重構耗時。